任杰 顧利萍 尤文龍

1)(常熟理工學(xué)院物理系,常熟 215500)

2)(蘇州大學(xué)物理與光電·能源學(xué)院,蘇州 215006)

1 引 言

在過(guò)去的二十年中,量子自旋系統(tǒng)中的量子相變一直是物理學(xué)家研究的熱點(diǎn)之一[1].這些研究當(dāng)中,自旋S=1海森伯模型也吸引了不少研究者的注意[2?4],其中原因之一是系統(tǒng)的基態(tài)為著名的Haldane相.這個(gè)相最顯著的特征之一是有非局域的弦序參量.另外一個(gè)特點(diǎn)是基態(tài)和自旋三重激發(fā)態(tài)之間是非簡(jiǎn)并的,這點(diǎn)和自旋為1/2的海森伯自旋鏈有著很大的差別.實(shí)驗(yàn)上發(fā)現(xiàn)很多材料為S=1的準(zhǔn)一維自旋鏈,例如Y2BaNi5[5],CsNiCl3[6],Dy2BaNiO5[7],Nd2BaNiO5[8].然而完美的一維海森伯自旋鏈在材料中很少出現(xiàn),或多或少會(huì)出現(xiàn)一些各向異性或者雜亂性以及其他類(lèi)型的復(fù)雜相互作用,如次近鄰相互作用甚至多體相互作用.值得一提的是,很多準(zhǔn)一維材料具有鋸齒形結(jié)構(gòu),次近鄰格點(diǎn)間的距離與最近鄰格點(diǎn)間的距離相比差別并不是很大,所以研究帶有次近鄰的相互作用以及多體相互作用的S=1自旋鏈?zhǔn)且患鞋F(xiàn)實(shí)意義的事情.最近,很多研究利用從量子信息中衍生出來(lái)的概念來(lái)研究量子多體系統(tǒng)的基態(tài)相變問(wèn)題,其中最常見(jiàn)的是利用量子糾纏熵和保真率探測(cè)量子多體系統(tǒng)中的量子臨界點(diǎn).大量的研究表明,這兩個(gè)觀測(cè)量在強(qiáng)關(guān)聯(lián)體系中對(duì)相變探測(cè)都是非常有效的[9?17],這是因?yàn)橄到y(tǒng)發(fā)生相變時(shí),系統(tǒng)的基態(tài)性質(zhì)會(huì)發(fā)生劇烈的變化,從而使得這兩個(gè)物理量也會(huì)相應(yīng)地發(fā)生劇烈的變化.基于這兩個(gè)量子信息觀測(cè)量的普適性,本文將利用它們研究有近鄰相互作用以及多體相互作用的S=1自旋鏈中的量子相變.

2 研究模型

系統(tǒng)的哈密頓量如下:

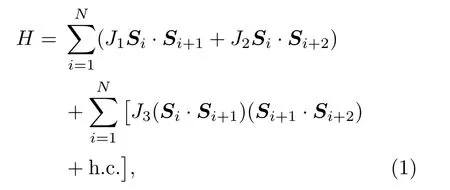
其中Si為i格點(diǎn)上的S=1的自旋算符;參數(shù)J1為近鄰的相互作用,假設(shè)J1=1;參數(shù)J2,J3分別代表次近鄰相互作用和三體相互作用;符號(hào)h.c.表示前一項(xiàng)的轉(zhuǎn)置共軛.此外,本文中采用了開(kāi)放的邊界條件,N代表自旋鏈的長(zhǎng)度.

3 量子信息度量與算法

量子保真度,一個(gè)來(lái)自量子信息理論的概念,可以用來(lái)探測(cè)物理系統(tǒng)中的量子相變.假設(shè)一個(gè)簡(jiǎn)單系統(tǒng),其系統(tǒng)的哈密頓量可以寫(xiě)成H(J3)=H0+J3HI,其中H0為主要部分,HI為驅(qū)動(dòng)部分,J3為HI的大小.如果ρ(J3)代表系統(tǒng)基態(tài)的密度矩陣,那么兩個(gè)基態(tài)ρ(J3)和ρ(J3+δJ3)之間的保真度定義如下:

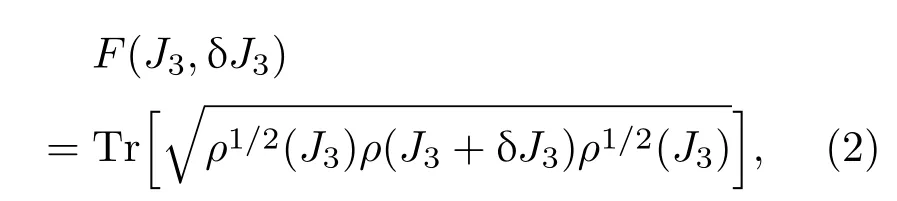
其中 δJ3是一很小的變化量.對(duì)于一個(gè)純態(tài),方程(2)可以寫(xiě)成

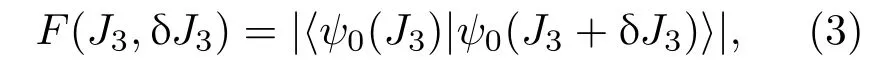
其表示兩個(gè)態(tài)的交疊程度.當(dāng)δJ3=0,保真度會(huì)達(dá)到其最大值F(J3,0)=1.為了δJ3避免任意性,一般采用平均保真率,其定義如下:

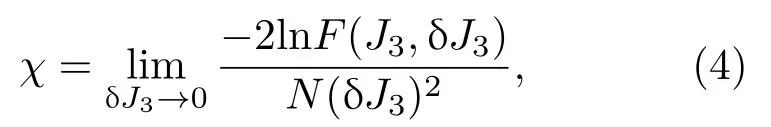
其與量子相變之間的關(guān)系已經(jīng)得到證實(shí)[10,11].

另一方面,糾纏熵被人們用來(lái)度量系統(tǒng)的兩體糾纏,其定義如下.假設(shè)|ψ0〉表示系統(tǒng)的基態(tài),系統(tǒng)可以分成A,B兩個(gè)部分,一般情況下,把第一個(gè)自旋到第L個(gè)看成A部分,剩下的部分就是B部分.其中A部分的約化密度矩陣可以表示為

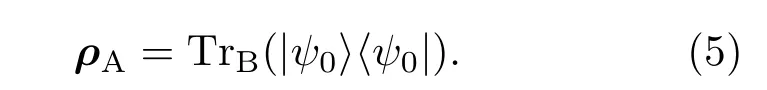
A,B部分之間的兩體糾纏可以表示為

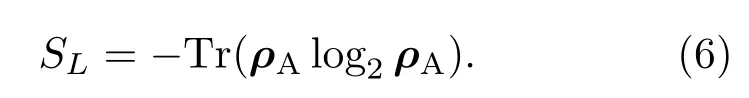
眾所周知,研究強(qiáng)關(guān)聯(lián)系統(tǒng)的一個(gè)典型難題就是系統(tǒng)希爾伯特空間的維度隨著粒子數(shù)的增加呈指數(shù)性增長(zhǎng).值得慶幸的是,利用密度矩陣重整化群的方法,可以得到大尺度的一維強(qiáng)關(guān)聯(lián)系統(tǒng)的近似基態(tài)[18,19],從而便于研究系統(tǒng)的特性.利用有限系統(tǒng)密度矩陣重整化群的方法,計(jì)算哈密頓量公式(1)的基態(tài),采用雙精度數(shù)據(jù)并保留了200個(gè)態(tài),使得截?cái)嗾`差在10?8以下.

4 數(shù)值結(jié)果

利用密度矩陣重整化群的方法計(jì)算了系統(tǒng)(1)基態(tài)的保真率隨J3的變化,其中系統(tǒng)的N達(dá)到55.圖1表示不同大小的系統(tǒng)的基態(tài)保真率與三體相互作用J3之間的關(guān)系.不同大小的系統(tǒng)的保真率都存在一個(gè)峰值,并且這個(gè)峰值隨著系統(tǒng)的增大而變大.峰值對(duì)應(yīng)的J3隨著N的增大而減小.眾所周知,保真度是度量?jī)蓚€(gè)態(tài)的相似度,而量子相變發(fā)生的時(shí)候,量子臨界點(diǎn)兩側(cè)的量子態(tài)相似度最低,所以保真率的峰值恰好對(duì)應(yīng)系統(tǒng)的相變點(diǎn),這正是我們用保真率探測(cè)相變的原因.保真率峰值對(duì)應(yīng)的J3有著如下的關(guān)系:

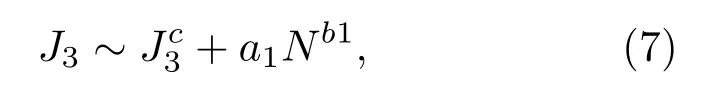
其中a1,b1是常數(shù),這個(gè)結(jié)果在圖1的插圖中顯示.得到a1=0.0352,b1=?0.247,.當(dāng)J3=0,系統(tǒng)處于Haldane相,當(dāng)J3很大時(shí),系統(tǒng)處在二聚物相.就是上述這兩種相的相變點(diǎn),這個(gè)結(jié)果和以前的研究結(jié)果一致[20].

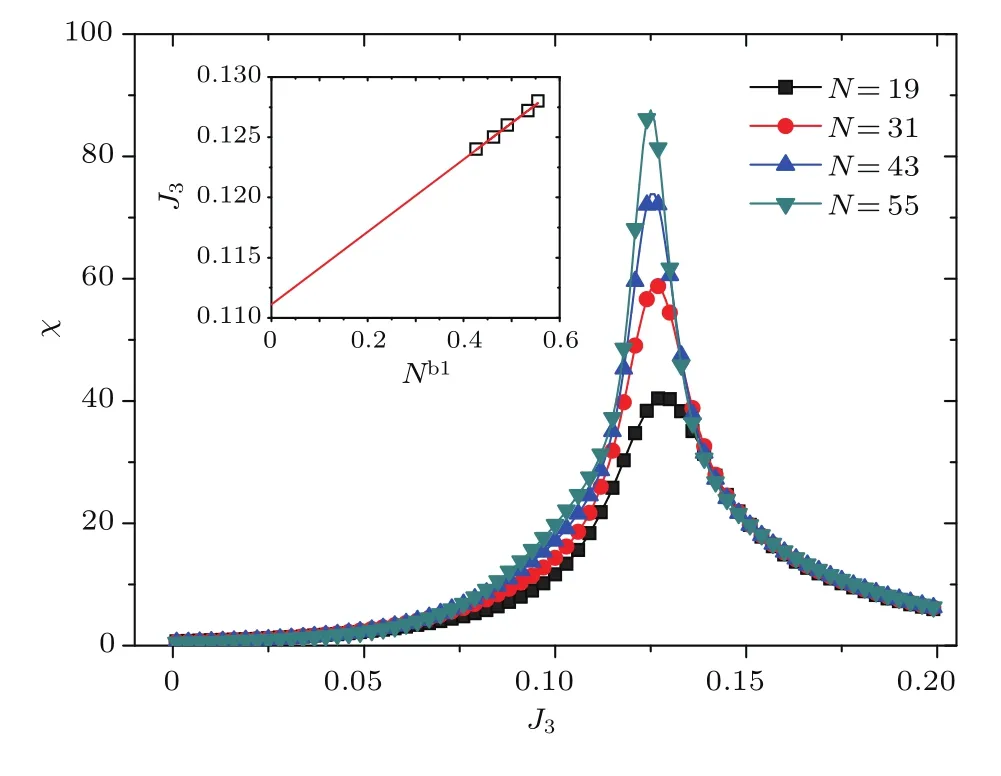
圖1 平均保真率隨三體相互作用J3的變化關(guān)系 其中J2=0,插圖為平均保真率極值對(duì)應(yīng)的的尺度效應(yīng),直線為擬合線Fig.1.The fi delity susceptibility per site is plotted as a function of the three-site interaction J3for different system sizes with J2=0.Inset: fi nite-size scaling ofof the fi delity susceptibility.The line is the fi t line.

此外,還研究了系統(tǒng)左邊部分和右邊部分之間的糾纏熵,其中L=(N+1)/2.圖2表示系統(tǒng)左邊部分和右邊部分之間的糾纏熵隨J3變化的關(guān)系.可以看出糾纏熵隨J3增大到達(dá)一個(gè)峰值,隨著J3的進(jìn)一步增大,糾纏熵迅速下降到0.此時(shí)J3=0.167,且不隨系統(tǒng)變化而變化.這表明這個(gè)點(diǎn)就是系統(tǒng)的Majumdar-Ghosh(MG)點(diǎn).對(duì)于任意的自旋,其MG對(duì)應(yīng)的位置可以表達(dá)為J3/J1=1/[4S(S+1)?2][21],這里S=1,很容易得到J3/J1=0.167,這驗(yàn)證了本文結(jié)果的正確性.

一般情況下,糾纏熵的極值對(duì)應(yīng)點(diǎn)就是系統(tǒng)的相變點(diǎn).擬合糾纏熵峰值對(duì)應(yīng)的位置隨系統(tǒng)N的變化關(guān)系,始終沒(méi)有得到這個(gè)點(diǎn).這說(shuō)明在此系統(tǒng)中該結(jié)論不成立.有時(shí)糾纏熵的極值對(duì)應(yīng)點(diǎn)不是系統(tǒng)的相變點(diǎn),而是糾纏熵一階導(dǎo)數(shù)的極值對(duì)應(yīng)點(diǎn)是系統(tǒng)的相變點(diǎn)[15,16,21].這是因?yàn)橄到y(tǒng)能量的二階導(dǎo)數(shù)部分往往對(duì)應(yīng)密度矩陣的一階導(dǎo)數(shù).圖2(b)表示糾纏熵的一階導(dǎo)數(shù)隨三體相互作用J3之間的關(guān)系.在J3=0.12附近糾纏熵的一階導(dǎo)數(shù)有極小值.通過(guò)(6)式擬合,很容易就得到,a2=0.029,b2=?0.195[見(jiàn)圖2(b)插圖].

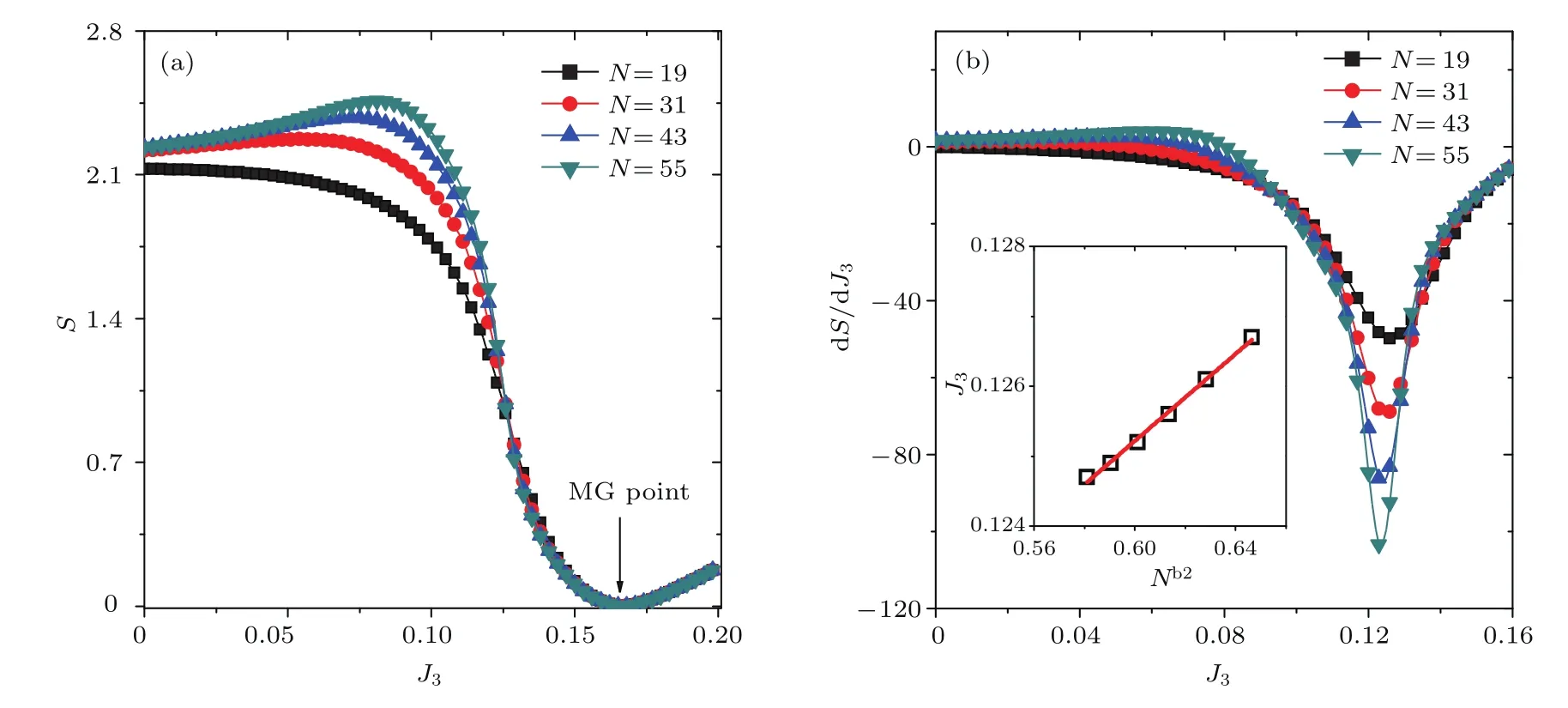
圖2 (a)糾纏熵和(b)其一階導(dǎo)數(shù)隨三體相互作用J3的變化關(guān)系 其中J2=0,(b)當(dāng)中的插圖為糾纏熵一階導(dǎo)數(shù)極值對(duì)應(yīng)的J3的尺度效應(yīng),直線為擬合線Fig.2.(a)The entanglement and(b)its fi rst deviation are plotted as a function of the three-site interaction J3for different system sizes with J2=0.Inset(b): fi nite-size scaling ofcome from the fi rst deviation of entanglement entropy.The line is the fi t line.

為了進(jìn)一步驗(yàn)證本文的結(jié)果,數(shù)值模擬了弦序參量,其結(jié)果在圖3中顯示.弦序參量的定義如下[22]:

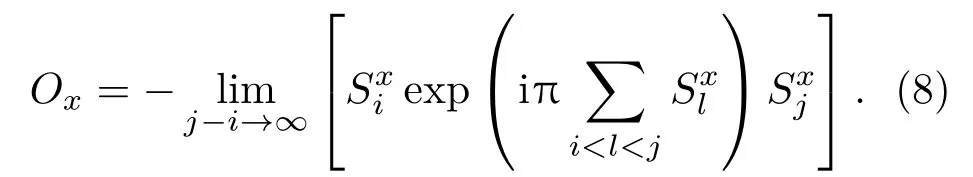
弦序參量可以探測(cè)Haldane相,因?yàn)樵贖aldane相中弦序參量為正值.從圖3可以看出,隨著J3的增長(zhǎng),弦序參量迅速下降為零,這表明系統(tǒng)從Haldane相變化到二聚物相.發(fā)現(xiàn)不同大小的系統(tǒng)弦序參量隨1/N呈線性關(guān)系,見(jiàn)圖3插圖.本文展示了J3=0.105和J3=0.115這兩種情況.若將N推廣到無(wú)窮,也就是1/N=0,研究發(fā)現(xiàn)Ox(J3=0.105)＞0,Ox(J3=0.115)＜0,這就表明在這兩種情況下系統(tǒng)處在不同的相.

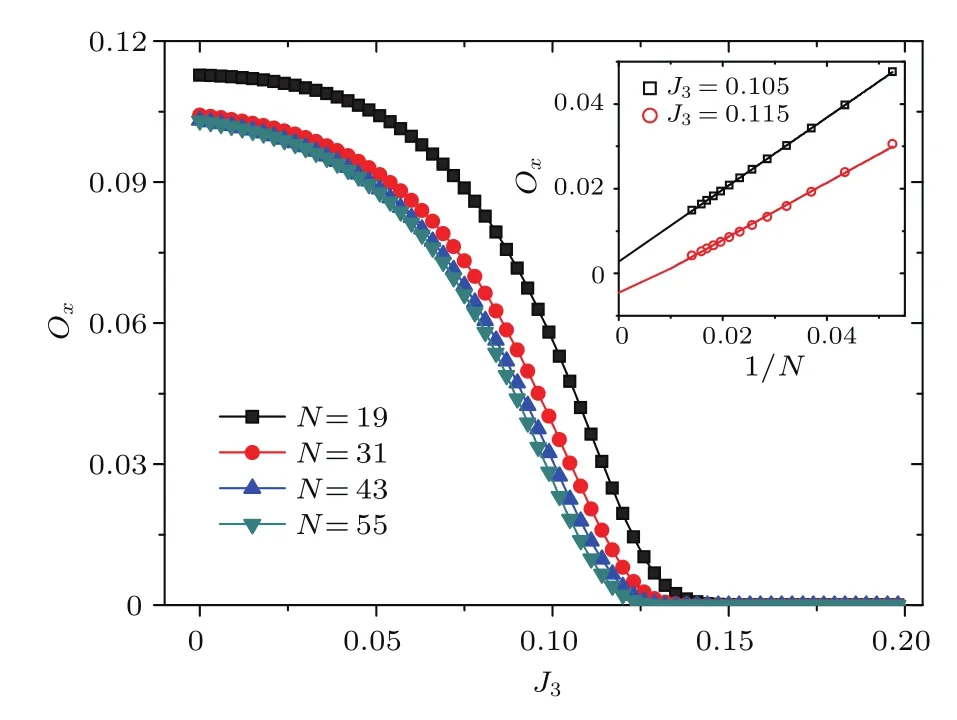
圖3 弦序參量隨三體相互作用J3的變化關(guān)系 其中J2=0;插圖為弦序參量的尺度效應(yīng),其中J3=0.105,J3=0.115Fig.3.The string order parameter is plotted as a function of the three-site interaction J3for different system sizes with J2=0.Inset:scaling of string order parameter with J3=0.105,J3=0.115.

進(jìn)一步研究J2=?0.3的情況,得到類(lèi)似的結(jié)果(見(jiàn)圖4).通過(guò)圖4(a)研究發(fā)現(xiàn)保真率的峰值停留在J3=0.212位置上,幾乎不隨系統(tǒng)N的改變而變化,說(shuō)明Haldane相與二聚物相間的相變點(diǎn)就在此點(diǎn).圖4(b)揭示了糾纏熵與J3變化關(guān)系,很容易看出糾纏熵為零的點(diǎn)也就是到MG點(diǎn)在J3=0.267.圖4(c)可以通過(guò)糾纏熵的一階導(dǎo)數(shù)的極值探測(cè)到量子相變點(diǎn).在此基礎(chǔ)之上,研究不同J2情況下的保真率和糾纏熵隨J3的變化關(guān)系,并得到其相變邊界.因此,本文進(jìn)一步展示了系統(tǒng)的相圖隨J2以及J3的變化關(guān)系(見(jiàn)圖5).J2＞0,J3＞0部分的相圖已經(jīng)在文獻(xiàn)[20]中顯示.當(dāng)J2=0時(shí),系統(tǒng)相變發(fā)生在J3=0.111,此相變屬于二級(jí)相變.隨著J2的增長(zhǎng),此相變會(huì)從二級(jí)相變轉(zhuǎn)化成一級(jí)相變.隨著J2的進(jìn)一步增長(zhǎng),會(huì)出現(xiàn)次近鄰的Haldane相與Haldane相的一級(jí)相變.眾所周知,保真率在探測(cè)一級(jí)相變會(huì)出現(xiàn)比二級(jí)相變時(shí)更尖銳的峰值[23,24].此外出現(xiàn)的次近鄰的Haldane與二聚物相之間的二級(jí)相變非常類(lèi)似于Haldane相與二聚物相之間的相變,保真率也能成功探測(cè)此相變.為了避免重復(fù),這里不再展示J2＞0,J3＞0部分的相圖,本文中只展示了J2＜0,J3＞0部分的相圖.隨著J2＜0的出現(xiàn),系統(tǒng)相變?nèi)詫儆诙?jí)相變,只是相變點(diǎn)增大.對(duì)于MG點(diǎn)也類(lèi)似的結(jié)論,并且相變點(diǎn)和MG點(diǎn)之間的差距也越來(lái)越小,最后重合在一起,成為相變邊界.

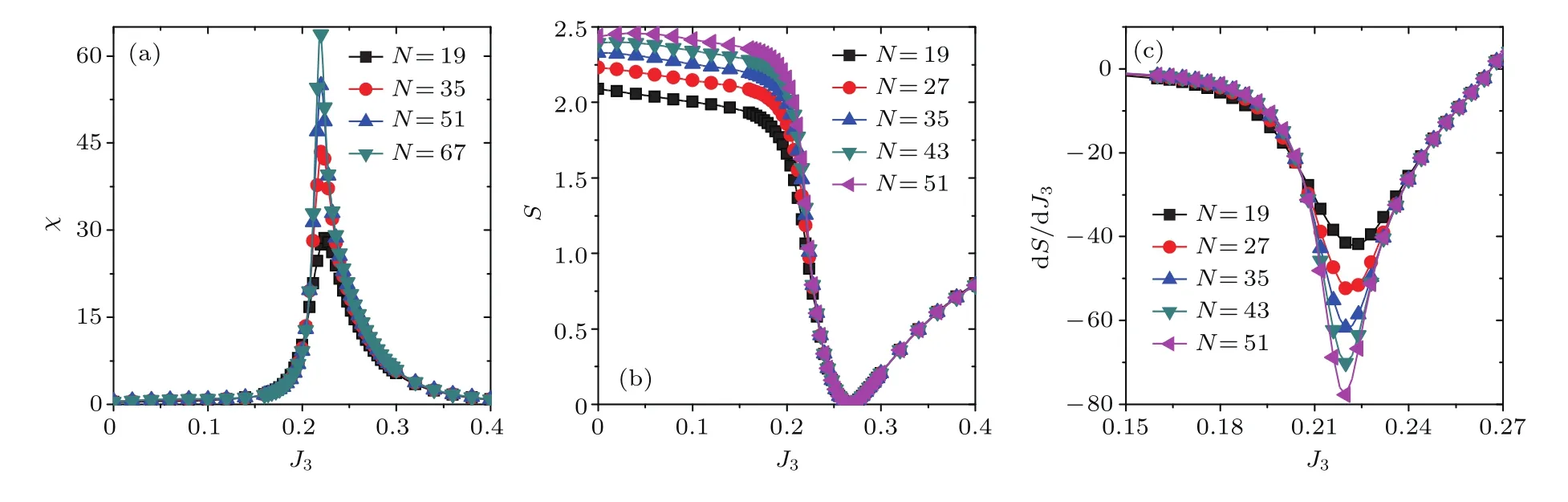
圖4 (a)平均保真率,(b)糾纏熵,(c)糾纏熵的一階導(dǎo)數(shù)隨三體相互作用J3的變化關(guān)系(J2=?0.3)Fig.4.(a)Fidelity susceptibility per site,(b)entanglement entropy,(c)the fi rst deviation of entanglement entropy are plotted as a function of the three-site interaction J3for different system sizes with J2= ?0.3.

圖5 系統(tǒng)的相變圖 其中J2＜0,J3＞0;黑線為Haldane與二聚物相變邊界,紅色線為MG點(diǎn)Fig.5.Phase diagram of a spin-1 Heisenberg chain with the interactions J2＜0 and J3＞0.The black indicates the boundary between Haldane phase and dimerized phase,and the red line indicate the MG pionts.

5 結(jié) 論

研究了帶有次近鄰相互作用和三體相互作用的自旋S=1一維自旋鏈中量子糾纏熵和量子保真率,并分析了這兩個(gè)量子觀測(cè)量與該系統(tǒng)中的量子相變之間的關(guān)系.研究結(jié)果表明系統(tǒng)存在的Haldane相與二聚物相之間的相變可以通過(guò)保真率以及糾纏熵的一階導(dǎo)數(shù)觀測(cè)到.這兩個(gè)量子信息觀測(cè)量在S=1的自旋鏈中被證實(shí)都是很不錯(cuò)的量子相變的指針,可以幫助我們進(jìn)一步了解該系統(tǒng).應(yīng)用這兩個(gè)量子信息觀測(cè)量來(lái)確定量子相變臨界點(diǎn)的優(yōu)越性在于它們可以幫助我們進(jìn)一步判定其他的序參量是否可靠.

[1]Sachdev S 1999Quantum Phase Transitions(Cambridge:Cambridge University Press)p133

[2]den Nijs M,Rommelse K 1989Phys.Rev.B40 4709

[3]Chen W,Hida K,Sanctuary B C 2003Phys.Rev.B67 104401

[4]DegliEspostiBoschiC,ErcolessiE,OrtolaniF,Roncaglia M 2003Eur.Phys.J.B35 465

[5]Darriet J,Regnault L 1993Solid State Commun.86 409

[6]Buyers W J L,Morra R M,Armstrong R L,Hogan M J,Gerlach P,Hirakawa K 1986Phys.Rev.Lett.56 371

[7]Singh K,Basu T,Chowki S,Mahapotra N,Iyer K K,Paulose P L,Sampathkumaran E V 2013Phys.Rev.B88 094438

[8]Zheludev A,Tranquada J M,Vogt T,Buttrey D J 1996Phys.Rev.B54 7210

[9]Li W,Andreas W,Delft J V 2013Phys.Rev.B88 245121

[10]You W L,Li Y W,Gu S J 2007Phys.Rev.E76 022101

[11]Cozzini M,Ionicioiu R,Zanardi P 2007Phys.Rev.B76 104420

[12]Ren J,Zhu S Q 2008Eur.Phys.J.D50 103

[13]Ren J,Xu X F,Gu L P,Li J L 2012Phys.Rev.A86 064301

[14]Ren J,Liu G H,You W L 2015J.Phys.:Condens.Matter27 105602

[15]Ren J,Zhu S Q 2009Phys.Rev.A79 034302

[16]Liu G H,Wang H L,Tian G S 2008Phys.Rev.B77 214418

[17]Zhao J H 2012Acta Phys.Sin.61 220501(in Chinese)[趙建輝2012物理學(xué)報(bào)61 220501]

[18]White S R 1993Phys.Rev.B48 10345

[19]Schollw?ck U 2005Rev.Mod.Phys.77 259

[20]Chepiga N,Affleck I,Mila F 2016Phys.Rev.B93 241108

[21]Michaud F,Vernay F,Manmana S R,Mila F 2012Phys.Rev.Lett.108 127202

[22]Wu L A,Sarandy M S,Lidar D A 2004Phys.Rev.Lett.93 250404

[23]Gu S J 2010Int.J.Mod.Phys.B24 4371

[24]You W L,Dong Y L 2011Phys.Rev.B84 174426