兩數(shù)和與差的完全平方公式的趣用
北京市第十三中學(xué)(100009) 岳博雅
兩數(shù)和與差的完全平方公式的趣用
北京市第十三中學(xué)(100009) 岳博雅
將兩數(shù)和與差的完全平方公式
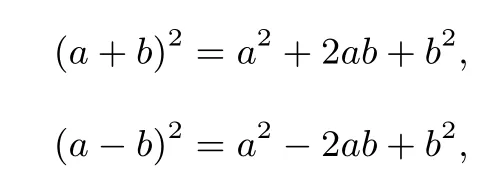
相加可得
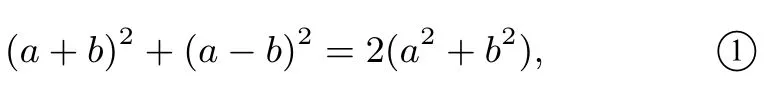
相減可得
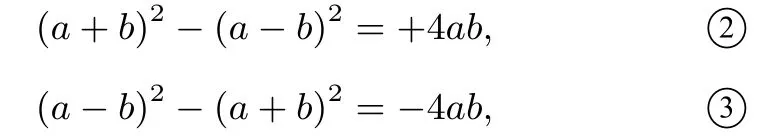
當(dāng)a,b為向量時(shí),公式①的幾何背景為:平行四邊形四邊的平方和等于兩對(duì)角線的平方和.它們?cè)谥袑W(xué)階段能起到簡(jiǎn)化計(jì)算的作用,達(dá)到又快又好的目的,還可以提增學(xué)習(xí)數(shù)學(xué)的興趣.
例1 [2012年中考江西省南昌市卷第8題3分]已知(m?n)2=8,(m+n)2=2,則m2+n2=____.
解由公式①立得2(m2+n2)=(m?n)2+(m+n)2= 8+2=10,故m2+n2=5.
評(píng)析 不必求出具體的m,n的值(實(shí)際上共有4組解且均為無(wú)理解).
例2[2011年中考天津市卷第10題3分壓軸題]若實(shí)數(shù)x,y,z滿足(x?z)2?4(x?y)(y?z)=0,則下列式子一定成立的是( ).
A.x+y+z=0 B.x+y?2z=0
C.y+z?2x=0 D.z+x?2y=0
解 由公式②得[(x?y)+(y?z)]2?[(x?y)?(y?z)]2= 4(x?y)(y?z),即(x?z)2?[x?2y+z]2=4(x?y)(y?z).又(x?z)2?4(x?y)(y?z)=0,所以x?2y+z=0,故選D.
評(píng)析 本題的常規(guī)解法是:x2?2xz+z2?4xy+4xz?4yz+4y2=0,即(x?2y+z)2=0.用到了三個(gè)數(shù)的和的完全平方公式.
例 3 [2016年中考浙江省杭州市卷第 10題 3分壓軸題]設(shè)a,b是實(shí)數(shù),定義關(guān)于@的一種運(yùn)算如下: a@b=(a+b)2?(a?b)2,則下列結(jié)論:
①若a@b=0,則a=0或b=0;
②a@(b+c)=a@b+a@c;
③不存在實(shí)數(shù)a,b,滿足a@b=a2+5b2;
④設(shè)a,b是矩形的長(zhǎng)和寬,若矩形的周長(zhǎng)固定,則當(dāng)a=b時(shí),a@b的值最大.
其中正確的是( ).
A. ②③④ B. ①③④
C. ①②④ D. ①②③
略解C.
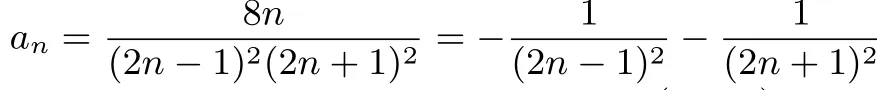
 中學(xué)數(shù)學(xué)研究(廣東)2017年10期
中學(xué)數(shù)學(xué)研究(廣東)2017年10期
- 中學(xué)數(shù)學(xué)研究(廣東)的其它文章
- 基本不等式為例談數(shù)學(xué)中的題型歸納
- 新課標(biāo)下初中數(shù)學(xué)思想方法的滲透
——基于函數(shù)與方程“融合”的探究 - 高中數(shù)學(xué)教學(xué)中的德育滲透
——以《數(shù)系的擴(kuò)充與復(fù)數(shù)的概念》課堂實(shí)錄為例 - 探尋初中數(shù)學(xué)規(guī)則課型教學(xué)
——以“直角三角形全等的判定”教學(xué)為例 - 初中數(shù)學(xué)講評(píng)課探究
- 多維思考引領(lǐng)教學(xué) 生態(tài)互動(dòng)激活課堂
——以一道高考試題的教學(xué)運(yùn)用為例
