馬榮,張玉龍

(1.西北工業(yè)大學(xué)理學(xué)院,陜西 西安 710072;2.西安交通大學(xué)電信學(xué)院,陜西 西安 710049)

關(guān)于 Lucas 數(shù)列同余性質(zhì)的研究

馬榮1,張玉龍2

(1.西北工業(yè)大學(xué)理學(xué)院,陜西 西安 710072;2.西安交通大學(xué)電信學(xué)院,陜西 西安 710049)

將二項(xiàng)式系數(shù)的性質(zhì)應(yīng)用到Lucas數(shù)列的研究中,并結(jié)合Fibonacci數(shù)列與Lucas數(shù)列的恒等式得到幾個(gè)有趣的Lucas數(shù)列的同余式.

Fibonacci數(shù)列;Lucas數(shù)列;恒等式;同余式

1 引言

當(dāng)n是素?cái)?shù)時(shí),知道Ln模n同余于1,這一性質(zhì)對(duì)部分n是合數(shù)的情況也成立.關(guān)于Fn與Ln的其它性質(zhì),請(qǐng)參見文獻(xiàn)[5-8].

2 幾個(gè)引理

為了證明定理,需要以下幾個(gè)引理.首先得到幾個(gè)關(guān)于Fn的新的恒等式.

引理2.1對(duì)任意非負(fù)整數(shù)m和n,有

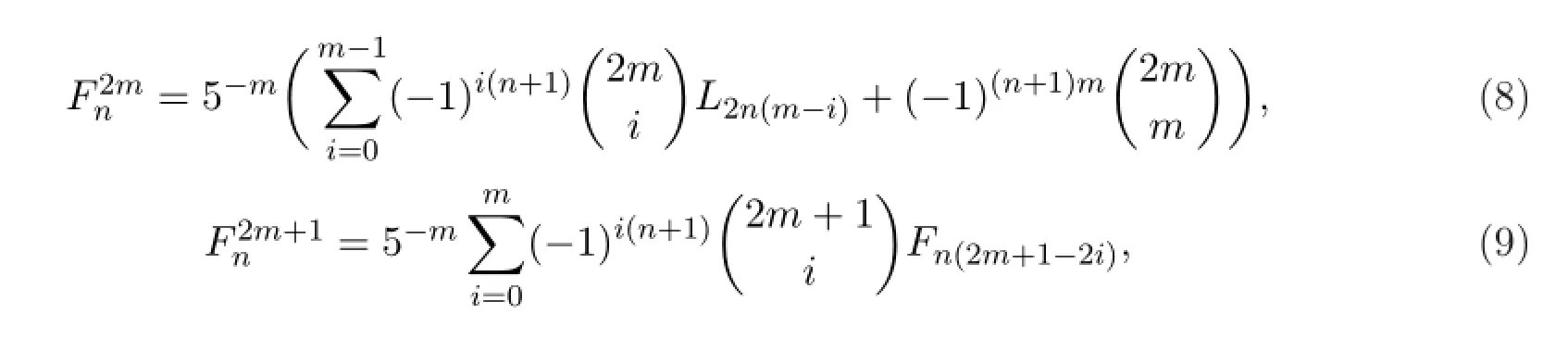
3 定理的證明

[1] Paulo Ribenboim. The New Book of Prime Number Records[M]. New York: Springer, 1996.

[2] Franz Lemmermeyer. Reciprocity Laws[M]. New York: Springer, 2000.

[3] Derek Jennings. Some polynomial identities for the Fibonacci and Lucas numbers[J]. The Fibonacci Quar- terly, 1993,31(2):134-137.

[4] Constance Brown. Fibonacci Analysis[M]. Hoboken: Bloomberg Press, 2008.

[5] Zhang Wenpeng. Some identities involving the Fibonacci numbers and Lucas numbers[J]. The Fibonacci Quarterly, 2004,42:149-154.

[6] Ma Rong. Zhang Wenpeng. Several identities involving the Fibonacci numbers and Lucas numbers[J]. The Fibonacci Quarterly, 2007,45:164-170.

[7] Duncan R L. Applications of uniform distribution to the Fibonacci numbers[J]. The Fibonacci Quarterly, 1967,5:137-140.

[8] Kuipers L. Remark on a paper by R. L. Duncan concerning the uniform distribution mod 1 of the sequence of the Logarithms of the Fibonacci numbers[J]. The Fibonacci Quarterly, 1969,7:465-466.

[9] Apostol Tom M. Intruduction to Analytic Number Theorem[M]. New York: Springer-Verlag, 1976.

On the congruence properties of the Lucas numbers

Ma Rong1,Zhang Yulong2

(1.School of Science,Northwestern Polytechnical University,Xi′an 710072,China; 2.The School of Electronic and In formation Engineering,Xi′an Jiaotong University,Xi′an 710049,China)

In this paper, we have used the properties of the binomial coe±cient to study the Lucas sequences, after combining the binomial coe±cient with the identities involving Fibonacci sequences and Lucas sequences, we have got several interesting congruence identities involving the Lucas sequences.

Fibonacci numbers, Lucas numbers, identities, congruence formula

O156.1

A

1008-5513(2012)02-0269-06

2011-07-29.

國(guó)家自然科學(xué)基金(11071194);西北工業(yè)大學(xué)基礎(chǔ)研究基金(JC 201123).

馬榮(1982-),博士,講師,研究方向：初等數(shù)論與解析數(shù)論.

2010 MSC:11B39,11B83