婁丹,謝離麗

(西北大學(xué)數(shù)學(xué)系,陜西 西安 710069)

擬線(xiàn)性熱方程的函數(shù)分離變量解

婁丹,謝離麗

(西北大學(xué)數(shù)學(xué)系,陜西 西安 710069)

用群狀結(jié)構(gòu)法研究擬線(xiàn)性熱方程的分離變量解,對(duì)于允許和型分離變量解的二階擬線(xiàn)性熱方程給出了一個(gè)完整的分類(lèi).說(shuō)明了一些帶有函數(shù)類(lèi)型反應(yīng)項(xiàng)的方程具有函數(shù)分離變量解,推廣了前人的結(jié)論.

函數(shù)分離變量解;群狀結(jié)構(gòu)法;擬線(xiàn)性熱方程

1 引言

本文研究帶有反應(yīng)項(xiàng)的擬線(xiàn)性熱方程

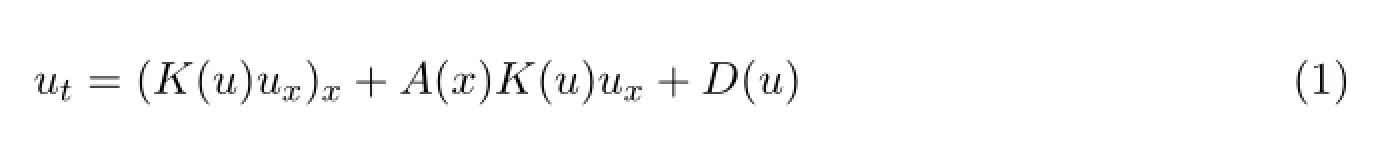
的函數(shù)分離變量解,其中K(u),D(u)均為足夠光滑的函數(shù).分離變量法是用來(lái)解決數(shù)學(xué)物理中的帶有初邊值條件偏微分方程的有效方法.李點(diǎn)對(duì)稱(chēng)的方法[1]在帶有變系數(shù)的線(xiàn)性偏微分方程的分離變量解的研究中扮演了十分重要的作用[2].對(duì)非線(xiàn)性的偏微分方程而言,一個(gè)自然的問(wèn)題就是它們是否存在分離變量解.因此,研究非線(xiàn)性偏微分方程的分離變量解是有意義的.例如文獻(xiàn)[3]對(duì)帶有熱源項(xiàng)的非線(xiàn)性反應(yīng)-擴(kuò)散方程

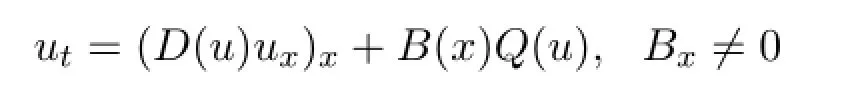
的函數(shù)分離變量解作了具體的研究.

對(duì)于(n+1)維非線(xiàn)性偏微分方程:

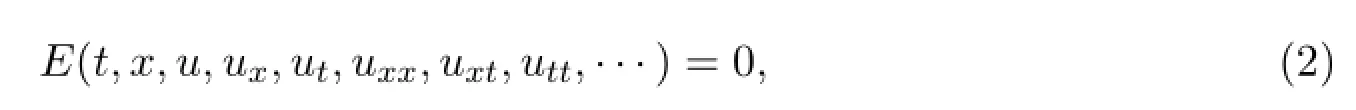
這里u=u(x,t),x=x(x1,x2,…).

如果方程(2)有形如u=φ(x)+ψ(t)的解,稱(chēng)之為和形式的分離變量解;如果方程(2)有形如u=φ(x)ψ(t)的解,則稱(chēng)之為乘積形式分離變量解.

如果方程(2)有形如f(u)=φ(x)+ψ(t)的解,這里f(u)/=u,f(u)/=ln u,稱(chēng)之為函數(shù)分離變量解.研究表明許多非線(xiàn)性偏微分方程有函數(shù)分離變量解.

文獻(xiàn)[3-5]中分別研究了方程:

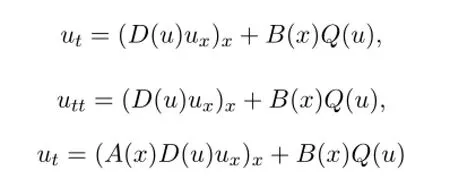
的函數(shù)分離變量解.

下面將討論帶有反應(yīng)項(xiàng)的擬線(xiàn)性熱方程(1)的函數(shù)分離變量解.

2 群狀結(jié)構(gòu)法

3 擬線(xiàn)性熱方程的函數(shù)分離變量解

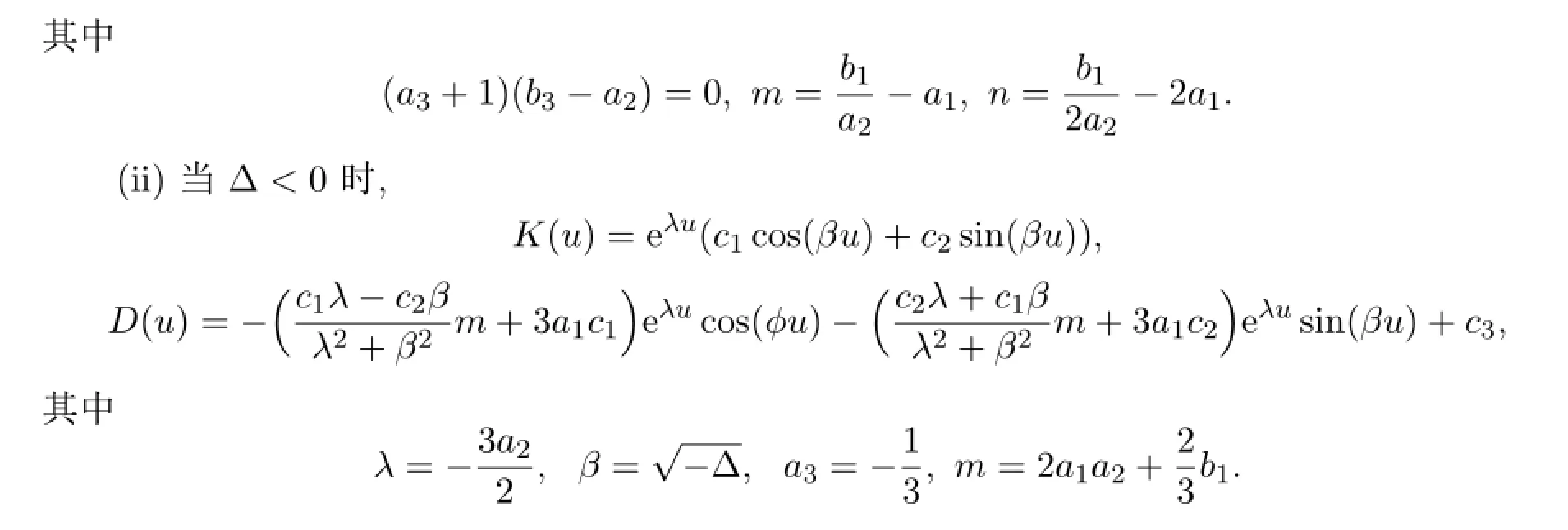
4 結(jié)論

本文利用群狀結(jié)構(gòu)法討論了擬線(xiàn)性熱方程的函數(shù)分離變量解問(wèn)題.結(jié)論是對(duì)于某些具有函數(shù)類(lèi)型反應(yīng)項(xiàng)的方程,能得到函數(shù)分離變量解.

[1] Bluman G W, Kuwei S. Symmetries and Differential Equation[M]. New York: Springer, 1989.

[2] Miller W. Symmetry and Separation of Variables[M]. Reading: Addison-Wesley, 1977.

[3] Qu C Z, Zhang S L. Group foliation method and functional separation of variables to nonlinear diffusion equation[J]. Chin. Phys. Lett., 2005,22(7):1563-1566.

[4] Qu C Z, Zhang S L. Extended group foliation method and functional separation of variables to nonlinear wave equations[J]. Commun. Theor. Phys., 2005,44:577-582.

[5] Hu J Y, Qu C Z, Yin Hui. Functional separable solutions to nonlinear diffusion equations by group foliation method[J]. Commun. Theor. Phys., 2007,47:193-199.

[6]左蘇麗.運(yùn)用群狀結(jié)構(gòu)法求非線(xiàn)性波方程的函數(shù)分離變量解[J].廈門(mén)大學(xué)學(xué)報(bào),2008,47(1):12-15.

[7]勾明.擬線(xiàn)性波方程的函數(shù)分離變量解[J].蘭州大學(xué)學(xué)報(bào):自然科學(xué)版,2009,45(1):107-111.

Functional separable solutions to quasi-linear heat equation

Lou Dan,X ie Lili
(Department of Mathematics,Northwest University,Xi′an 710069,China)

In this paper, we considered the separable solutions to the quasi-linear heat equation with the group foliation method. A classification was carried out for the second order heat equations which admit additive separable solutions. The result is an extension of some known conclusions about the functional separation of variable solutions.

functional separable solution, group foliation method, quasi-linear heat equation

O175.2

A

1008-5513(2012)02-0242-05

2011-05-20.

國(guó)家自然科學(xué)基金(10671156).

婁丹(1985-),碩士生,研究方向:偏微分方程.

2010 MSC:38Q80