Observation of spin-glass behavior in 1111-type magnetic semiconductor(La,Ba)(Zn,Mn)SbO
Xueqin Zhao(趙雪芹), Jinou Dong(董金甌), Rufei Zhang(張茹菲), Qiaolin Yang(楊巧林),Lingfeng Xie(謝玲鳳), Licheng Fu(傅立承), Yilun Gu(顧軼倫),Xun Pan(潘洵), and Fanlong Ning(寧凡龍),2,3,4,?
1Zhejiang Province Key Laboratory of Quantum Technology and Device and School of Physics,Zhejiang University,Hangzhou 310027,China
2State Key Laboratory of Silicon and Advanced Semiconductor Materials,Zhejiang University,Hangzhou 310027,China
3Collaborative Innovation Center of Advanced Microstructures,Nanjing University,Nanjing 210093,China
4Science and Technology Innovation Center,Chifeng High-Tech Industrial Development Zone,Chifeng 025250,China
Keywords: magnetic semiconductors,spin-glass,negative magnetoresistance
1.Introduction
The research of spintronics is devoted to manipulating both charge and spin freedom of electrons.[1-3]As an important branch in spintronics, magnetic semiconductors (MSs)provide a new perspective for the preparation of novel electronics devices.III-V MS (Ga,Mn)As is the most wellinvestigated system,[4]which is more compatible with optoelectronic devices applied in industry.In the mid-1990s, the fabrication of(Ga,Mn)As films made significant progress via low temperature molecular beam epitaxy (LT-MBE) method.With the injection of spin-polarized carriers,(Ga,Mn)As provides a new choice for the preparation of multifunctional heterojunctions with non-magnetic semiconductor GaAs.For example, Ohnoet al.has successfully prepared spin-polarized light-emitting diode (Spin-LED) based on (Ga,Mn)As.[5]At present,the Curie temperature(TC)of(Ga,Mn)As has reached~190 K-200 K,[6,7]which is still below room temperature.Moreover, the inequivalent substitutions of(Ga3+, Mn2+)introduce carriers and magnetic moments simultaneously,which makes it difficult to control carrier densities and magnetic moments independently.In addition, the MBE method is a nonequilibrium growth method, which makes the properties of materials sensitive to the growth conditions and may cause defects during the growth process.These challenges have aroused great interest in exploring more novel MSs, if possible,with higherTC.
In recent years, several series of bulk Zn-based MSs with decoupled carrier and spin doping have been reported,including 111-type Li(Zn,Mn)As,[8]Li(Cd,Mn)P,[9]122-type(Ba,K)(Zn,Mn)2As2,[10](Ca,Na)(Zn,Mn)2Sb2,[11]1111-type (La,Ba)(Zn,Mn)AsO,[12]La(Zn,Mn,Cu)SbO,[13]2114-type Cu2(Zn,Mn)(Sn,Al)Se4.[14]The equivalent substitutions of (Zn2+,Mn2+) result in higher chemical solubility of magnetic atoms, compared with III-V MSs.TheTCof(Ba,K)(Zn,Mn)2As2has reached~230 K,[15]which is already higher than that of(Ga,Mn)As.On the other hand,bulk semiconductor materials enable the measurements of microscopic probes,such as neutron scattering,nuclear magnetic resonance(NMR) and muon spin relaxation (μSR),[10,12,16]which has demonstrated that these bulk MSs share the same mechanism of ferromagnetic ordering as that of(Ga,Mn)As.
Unlike the magnetic semiconductors mentioned above,which can exhibit long-range ferromagnetic ordering, some magnetic semiconductors exhibit spin-glass behavior.[17]Back to 1980’s,when doping Mn into II-VI semiconductors such as ZnTe and HgTe, spin-glass ordering states had been usually observed in (Zn,Mn)Te[18]and (Hg,Mn)Te.[19]The reason is that the iso-valent substitution of Zn or Hg by Mn only introduces magnetic moments, and there are no enough carriers to build up the long-range ferromagnetic ordering.On the other hand,in some recently reported bulk form MSs,such as Ba(Zn,Mn,Cu)2As2[20]and Na(Zn,Mn)Sb,[21]spin-glass ordering state or glassy ferromagnetism has also been observed.These spin-glass state could be ascribed to the magnetic frustration generated by the competition between the indirect ferromagnetic and direct antiferromagnetic interactions.
As a valuable method in the study of magnetic condensed materials,pressure has been extensively applied to explore the mechanism of magnetic interactions, especially in magnetic semiconductors where ferromagnetic interactions are mediated by carriers.At present, the effect of physical pressure and chemical pressure on ferromagnetism in MSs has been widely studied.For example, in traditional III-V MS(In,Mn)Sb,TChas increased by 25%under a hydrostatic pressure of 2.7 GPa.[22]In addition,in n-type MS Ba(Zn,Co)2As2,the substitutions of(Ba,Sr)and(As,Sb)introduce positive and negative chemical pressure, respectively, and it was found that negative chemical pressure reducedTC, while positive chemical pressure increasedTCby 18%.[23]Previously, starting from the narrow band-gap semiconductor LaZnSbO,MSs(La,Ca)(Zn,Mn)SbO[24]and (La,Sr)(Zn,Mn)SbO[25]with the maximumTC~40 K and~27 K have been reported.We note that for the same doping level,TCis~20 K for(La0.95Ca0.05)(Zn0.95Mn0.05)SbO, whileTCis~14 K for(La0.95Sr0.05)(Zn0.95Mn0.05)SbO.This is largely because the ionic radius of Sr2+is larger than that of Ca2+, that is, negative chemical pressure suppressesTC.
In this paper, we attempt to synthesize (La, Ba)(Zn,Mn)SbO, and explore how chemical pressure will affect the magnetic properties in whole (La,AE)(Zn,Mn)SbO (AE=Ca, Sr, Ba) system.The substitutions of (La3+,Ba2+) and(Zn2+,Mn2+)in the parent compound LaZnSbO introduce carriers and local magnetic moments, respectively.Next, we fix the doping levelxof Ba2+at 0.05 and change the amount of magnetic atoms Mn, and explore how the spin densities affect magnetism in (La0.95Ba0.05)(Zn1-xMnx)SbO (x=0.025,0.05,0.075,0.10).The DC magnetization measurements show the presence of short-range ferromagnetic correlations in our specimens.The AC magnetic susceptibility measurements demonstrate that (La,Ba)(Zn,Mn)SbO exhibits the characteristics of spin-glass ordering state below spin freezing temperatureTf, rather than long-range ferromagnetic ordering as in(La,Ca)(Zn,Mn)SbO and (La,Sr)(Zn,Mn)SbO.A local maximum of resistance and negative magnetoresistance under an applied magnetic field have been observed, resulting from multiple interactions between quantum localization and carrier correlations.[26]With more Mn doping, resistivity increases significantly, which is attributed to the scattering of carriers caused by magnetic fluctuations.
2.Experiments
Polycrystalline samples (La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10)were prepared through the solidstate reaction method.First of all, high-purity La (99.9%,Alfa Aesar), Ba (99.2%, Alfa Aesar), Zn (99.9%, Alfa Aesar), MnO (99.5%, Aladdin), and Sb (99.999%, Prmat) were mixed according to the nominal composition.The mixtures were placed in the aluminum crucibles,sealed in evacuated silica tubes,then heated to 900?C and kept for 24 h.The precursors were fully grounded and pressed into pellets with 8 mm in diameter,then placed in aluminum crucibles,and sealed in evacuated silica tubes.Subsequently, the pellets were heated to 1100?C and kept for 40 h.All procedures except evacuating silica tubes are conducted in a glove box filled with high-purity argon.
To determine the crystal structure of polycrystalline samples LaZnSbO and(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05, 0.075, 0.10), the powder x-ray diffraction was carried out by a powder x-ray diffractometer (Model EMPYREAN)with monochromatic Cu-Kα1radiation.The lattice parameters were calculated by Rietveld refinements using open-source GSAS-II package.[27]The DC magnetization was measured on a Quantum Design magnetic property measurement system(MPMS-3).The AC magnetic susceptibility and magnetoresistance were measured on a Quantum Design physical property measurement system(PPMS).Four-probe technique was applied to the measurements of electrical resistivity.
3.Results and discussion
We show the x-ray diffraction patterns in the 2θrange of 10?-100?for polycrystalline samples LaZnSbO and(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10)in Fig.1(a).The diffraction peaks are consistent with a ZrCuSiAs-type tetragonal structure(space groupP4/nmm),as shown in the inset of Fig.1(b).The Rietveld refinement for(La0.95Ba0.05)(Zn0.95Mn0.05)SbO is plotted in Fig.1(b).The resultant weighted reliable factorRwpis 7.189%, indicating that the samples are in good quality.LaZnSbO share the same structure as that of the direct-gap semiconductor LaZnAsO[28]and Fe-based layered superconductor LaFeAsO1-δ.[29]The structure of LaZnSbO can be described as the stacking of[LaO]+layers and [ZnSb]-layers alongcaxis.[30]A few small peaks (marked as?) are observed in some samples.These are non-magnetic impurities ZnSb, and will not affect the discussion of magnetism in the following.
The calculated lattice parametersaandcof parent compound LaZnSbO are 4.2285 ?A and 9.5414 ?A, respectively,which is close to previously reported valuesa=4.2260 ?A andc=9.5369 ?A.[31]In Fig.1(c), we can see that the lattice parametersaandcof(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05, 0.075, 0.10) monotonically increase with the increasing of Mn doping, which is due to the fact that the ionic radius of Mn2+is larger than that of Zn2+.Obviously, with the Mn doping level increasing, the unit cell volume also increases monotonically, as shown in Fig.1(d).These provide strong evidences for the successful solution of (La3+,Ba2+)and(Zn2+,Mn2+).
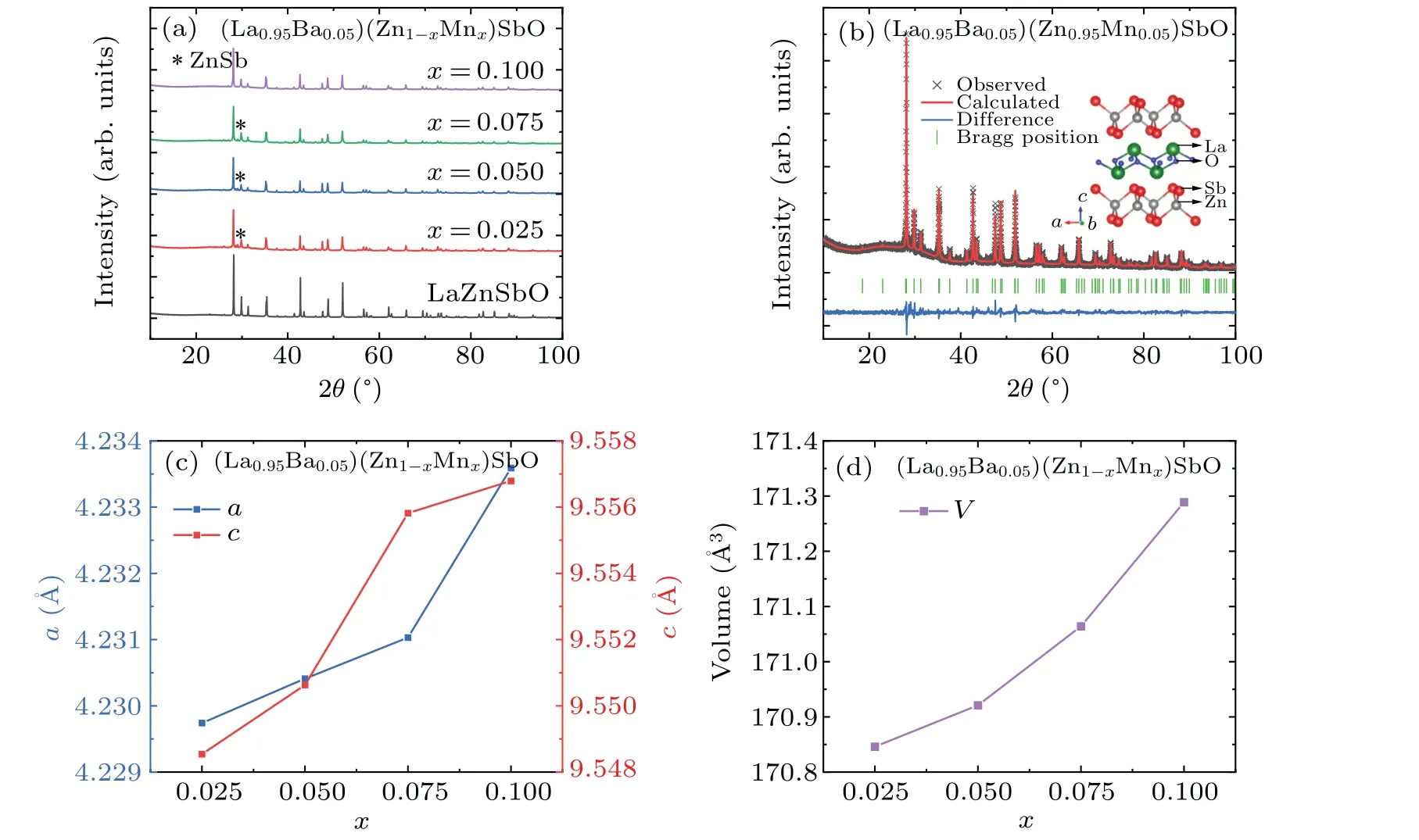
Fig.1.(a)The powder x-ray diffraction patterns for polycrystals LaZnSbO and(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10).The stars(?)represent the traces of impurities ZnSb.(b)The Rietveld refinement for(La0.95Ba0.05)(Zn0.95Mn0.05)SbO.Inset is the crystal structure of parent compound LaZnSbO.(c)The lattice parameters a and c obtained from the Rietveld refinements for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10).(d)The unit cell volume(V)versus doping level x for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10).
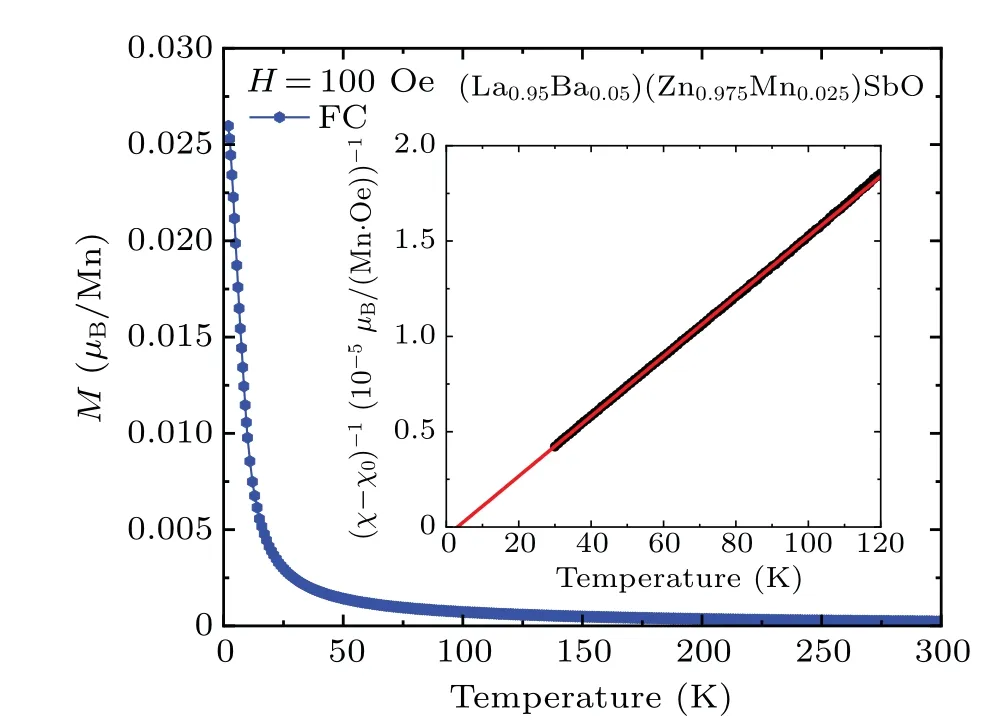
Fig.2.The temperature dependence of DC magnetization M of(La0.95Ba0.05)(Zn0.975Mn0.025)SbO under field-cooling condition in an external field Hext=100 Oe.Inset is the plot of 1/(χ-χ0)versus temperature.The black solid circles are the data,and the red straight line is a linear fitting of the Curie-Weiss law.
In Fig.2, we show the temperature dependence of DC magnetization(M)under field-cooling modes with the external fieldHext= 100 Oe for (La0.95Ba0.05)(Zn0.975Mn0.025)SbO.We did not observe obvious magnetic transition in the entire temperature range.We fit the data of high temperature region using the Curie-Weiss law and show it in the inset of Fig.2.The obtained Weiss temperature (θ) is~3.0 K.Positiveθindicates that the exchange interaction is ferromagnetic.However, this value is too small, we will not focus on(La0.95Ba0.05)(Zn0.975Mn0.025)SbO in the following.
In Fig.3(a), we show the temperature dependence of DC magnetization under zero-field-cooling (ZFC) and fieldcooling (FC) modes in an applied fieldHext= 100 Oe for(La0.95Ba0.05)(Zn1-xMnx)SbO (x=0.05, 0.075, 0.10).Magnetization suddenly increases around 20 K-30 K.In addition,the magnetization under FC mode at the base temperature of 2 K,Mbase, is~0.020μB/Mn forx=0.05, then increases to 0.028μB/Mn forx=0.075,and decreases to 0.017μB/Mn forx=0.10.This probably arises from the competition between ferromagnetic and antiferromagnetic interactions among Mn atoms.The probability that two Mn atoms at the nearestneighbor (NN) sites satisfiesP=C14x(1-x)3.For example,for the doping level ofx=0.075,the probability of finding one Mn atom at its NN sites isP=C14×0.075×0.9253=23.74%,andPincreases to 29.16% forx=0.10.With the increasing of Mn atoms, the possibility of Mn atoms at the NN sites increases, which enhances antiferromagnetic interactions.That is,doping too many Mn atoms is detrimental to the ferromagnetic interactions.
For the purpose of quantifying the temperature of magnetic transition, we plot dM(T)/dTversusTin Fig.3(c).With the increasing of Mn doping, the minimum values of dM(T)/dT(defined asTdif) increase first and then decrease.On the other hand, we fit the magnetic susceptibility curves at the high temperature region using the Curie-Weiss lawχ=χ0+C/(T-θ),Cis the Curie constant related to the effective magnetic moment,χ0is a temperature-independent term, andθis the Weiss temperature.The fitting results of 1/(χ-χ0) versus temperature under FC mode are shown in Fig.3(d).The Weiss temperaturesθare the intersections of the fitting lines with thexaxis.θis 8 K forx=0.05, then increases to 19 K forx=0.075, and decreases to 15 K forx=0.10.The positive values of the Weiss temperaturesθimply the establishment of ferromagnetic correlation between distant Mn atoms.We find thatTdifandθhave the same trend with the change of doping levelx.That is, both increase at first and decrease afterwards with the increasing of Mn doping levelx.This reflects that more Mn atoms suppress the ferromagnetic interactions, which is attributed to the competition between the short-range antiferromagnetic interactions among the NN Mn atoms and long-range ferromagnetic interactions induced by itinerant electrons.[32]
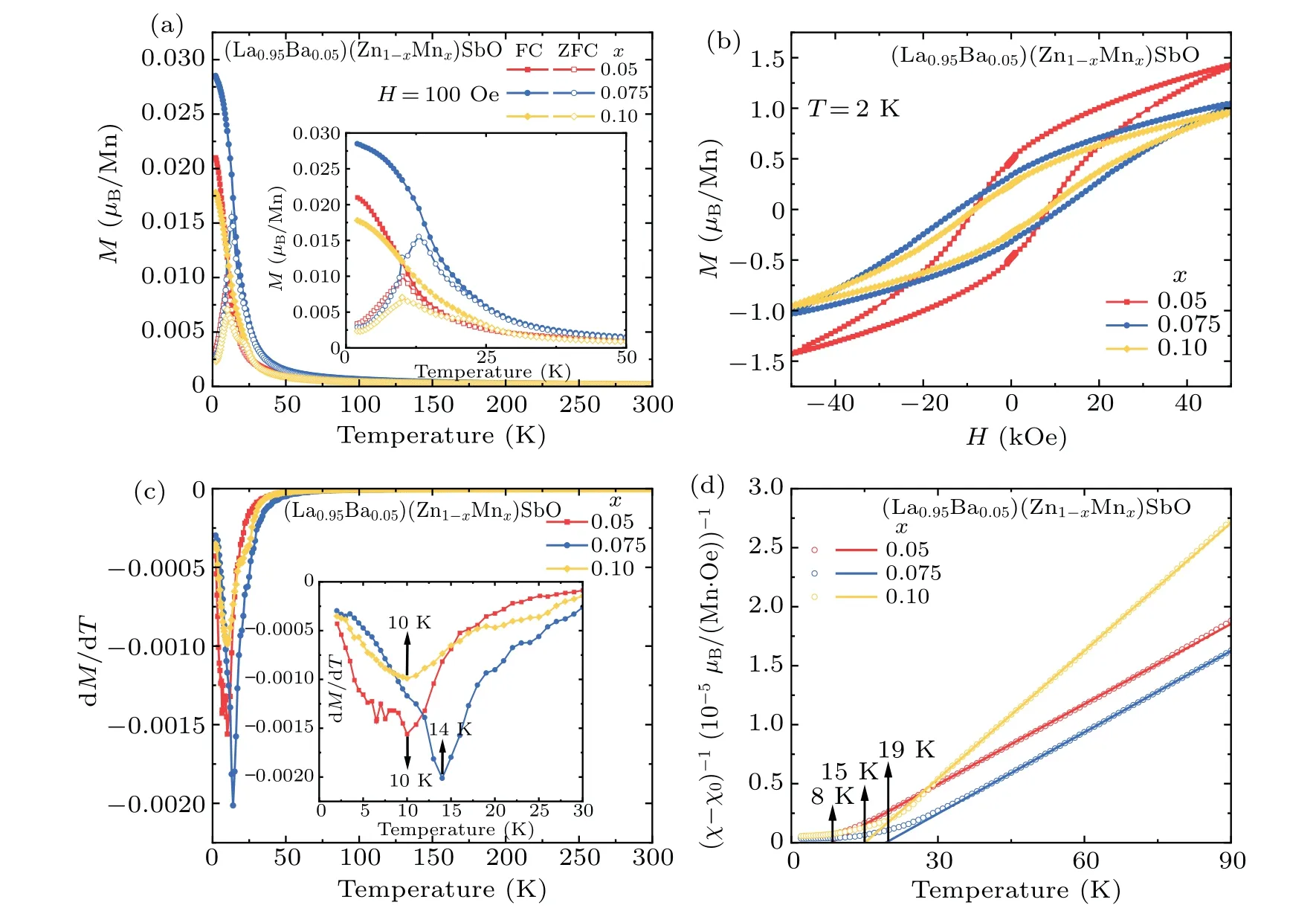
Fig.3.(a)The temperature dependence of DC magnetization for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10)in zero-field-cooling(ZFC)and field-cooling(FC)modes with Hext=100 Oe.Inset shows the enlarged M(T)curves for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10).(b)The iso-thermal magnetization for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10)measured at 2 K.(c)The dM(T)/dT versus T plots for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10).Inset shows an enlargement of 2 K to 30 K region,and arrows mark the position of the minimum values of dM(T)/dT.(d)The curves of 1/(χ-χ0)versus T for(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10).The lines represent the fitting of Curie-Weiss law,and arrows mark the Weiss temperatures θ.
We show the iso-thermal magnetization measured at 2 K for (La0.95Ba0.05)(Zn1-xMnx)SbO (x=0.05, 0.075, 0.10) in Fig.3(b).Clear hysteresis can be observed, demonstrating the presence of ferromagnetic interactions.The coercive field(HC)is~8400 Oe forx=0.05,then increases to~11500 Oe forx= 0.075, and decreases to~8150 Oe forx= 0.10.We calculate the effective magnetic moment(μeff)by formulaC=Nμ0μ2eff/3kB.The obtained parameters are listed in Table 1.

Table 1.The minimum values (Tdif) of dM(T)/dT, the Weiss temperature θ, the effective magnetic moment μeff, the base temperature moment Mbase, and the coercive field HC for (La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.05,0.075,0.10).
The Arrot-Noakes plots[33,34](M2versusH/M)obtained from iso-thermal magnetization at different temperatures for(La0.95Ba0.05)(Zn0.925Mn0.075)SbO are displayed in Fig.4.No indication of spontaneous magnetization is observed.Combined with the iso-thermal magnetization curves shown in Fig.3(b), where magnetization is still not saturated with the external magnetic field up to 5 T, we can say that it is not a long-range ferromagnetic ordering but a short-range spin-glass ordering state.

Fig.4.The Arrott plots of (La0.95Ba0.05)(Zn0.925Mn0.075)SbO under various temperatures.
To further determine whether the samples is in a spinglass ordering state, we conduct the AC magnetic susceptibility for (La0.95Ba0.05)(Zn0.925Mn0.075)SbO under an external AC field amplitude of 10 Oe with different frequencies(f).The cusp positions of the real partχ′in Fig.5(a)and the imaginary partχ′′in Fig.5(b)are obviously frequency-dependent.With the increasing of frequency,the real partχ′and the imaginary partχ′′move towards the higher temperature region,and the magnitude reduces slightly.We define the cusp position of the real partχ′as the static spin freezing temperature(Tf).According to the formulaK=?Tf/[Tf?logf],[35]we obtain the value ofKin Fig.5(c).TheK ~0.055 is whin the range of canonical spin-glass system(K ~0.005-0.08),[36]this indicates that the samples exhibit a spin-glass ordering state belowTf.The random arrangement of Mn atoms in lattice induces not only ferromagnetic but also antiferromagnetic interactions among Mn atoms.Their competition induces the spin-glass ordering state.The similar behavior has also been observed in Ba(Zn,Mn,Cu)2As2.[20]
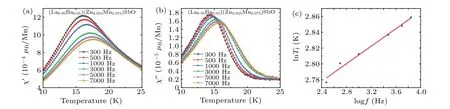
Fig.5.The (a) real part χ′ and (b) imaginary part χ′′ of AC magnetic susceptibility for (La0.95Ba0.05)(Zn0.925Mn0.075)SbO at different frequencies f.(c)The frequency dependence of spin freezing temperature Tf plotted as lnTf versus log f for(La0.95Ba0.05)(Zn0.925Mn0.075)SbO.
We performed the electrical transport measurements on the parent compound LaZnSbO and doped samples(La0.95Ba0.05)(Zn1-xMnx)SbO(x=0.025,0.05,0.075,0.10).The curves of the temperature-dependent electrical resistivityρ(T)are shown in Fig.6(a).The parent compound LaZnSbO shows the semiconducting behavior, as shown in the inset of Fig.6(a).After the solid solution of(La,Ba)and(Zn,Mn),resistivityρ(T) still retains the semiconducting behavior.On the other hand, with the increasing of the Mn-doped levelsx,the magnitude of the resistivity increases significantly.This can be attributed to the scattering of carriers by spins at low temperatures.
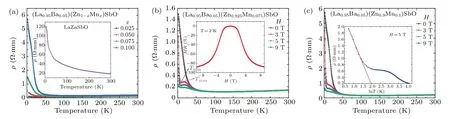
Fig.6.(a) The temperature-dependent resistivity ρ(T) for LaZnSbO (inset) and (La0.95Ba0.05)(Zn1-xMnx)SbO (x=0.025, 0.05, 0.075, 0.10).(b) The magnetoresistance for (La0.95Ba0.05)(Zn0.925Mn0.075)SbO under the external field Hext =0 T, 3 T, 5 T, 7 T, 9 T.The inset shows the field dependence of magnetoresistance(MR ≡[ρ(H)-ρ(0)]/ρ(0))measured in an external field ranging from 0 T to-9 T and 0 T to 9 T at 2 K.(c)The magnetoresistance of(La0.95Ba0.05)(Zn0.9Mn0.1)SbO with Hext=0 T,3 T,5 T,7 T,9 T.Inset shows resistivity ρ(T)versus lnT under Hext=5 T.
In Fig.6(b), we show the temperature-dependent magnetoresistance curves for (La0.95Ba0.05)(Zn0.925Mn0.075) SbO under the field of 0 T, 3 T, 5 T, 7 T, 9 T, respectively.The resistivity is suppressed rapidly with the increasing of applied magnetic field, that is, the negative magnetoresistance occurs.As the temperature goes down, a local maximum of resistivity (as marked byTmaxin Fig.6(b)) occurs under an applied magnetic field.Similar phenomenon has been observed in many MSs, such as traditional III-V compound(Ga,Mn)As,and novel bulk materials(Sr,Na)(Zn,Mn)2As2[37]and (Ba,K)(Cd,Mn)2As2.[26]This field-induced insulator-tometal transition is probably caused by multiple interactions between quantum localization and carrier correlations.[26]In(Ga,Mn)As system,the behavior of resistivity maximum near the Curie temperatureTCand associated negative magnetoresistance are ascribed to the existence of randomly oriented ferromagnetic bubbles,which drives efficient spin-disorder scattering of carriers,and thus reduces the anti-localization quantum corrections to conductivity.[38,39]Subsequently, as the temperature continues decreasing, a local minimum of resistance (as marked byTminin Fig.6(b)) occurs, followed by a strong upturn.The suppression of spin-dependent scattering in an external magnetic field leads to large negative magnetoresistance (MR ≡[ρ(H)-ρ(0)]/ρ(0)).As shown in the inset of Fig.6(b), for (La0.95Ba0.05)(Zn0.925Mn0.075)SbO, theMRreaches up to-88% under 9 T.Such a colossal negative magnetoresistanceMRhas also been observed in spin-glass(Cd,Mn)Se.[17]
Compared with the doping levelx=0.075 in Fig.6(b),when the doping levelxincreases to 0.1 as shown in Fig.6(c),the magnitude of resistivity is lifted up.In the inset of Fig.6(c), the resistivity for(La0.95Ba0.05)(Zn0.9Mn0.1)SbO at low temperature underHext=5 T linearly depends on lnT,which mimics that of the Kondo effect.[40]This phenomenon could also be interpreted by quantum corrections to the conductivity in the weakly localized regime,[38,39,41]because spin polarization of carriers destroys the Kondo effect.[39]
4.Discussion and conclusion
The ionic radius of Ca2+, Sr2+, and Ba2+are 0.99 ?A,1.13 ?A, and 1.35 ?A, respectively.Replacing La3+with Ca2+, Sr2+, and Ba2+respectively is expanding the lattice successively, which is equivalent to inducing negative chemical pressure into the system.Thus, the expansion of lattice causes Zn/Mn-Sb bond length to increase continuously, and p-d hybridization between local moments and hole carriers is weaken, which results in the suppression of ferromagnetic interactions.[42]Comparing the whole(La0.95AE0.05)(Zn0.95Mn0.05)SbO (AE=Ca, Sr, Ba) system,the magnetization under FC mode at the base temperature of 2 K is~0.60μB/Mn for (La0.95Ca0.05)(Zn0.95Mn0.05)SbO,0.15μB/Mn for (La0.95Sr0.05)(Zn0.95Mn0.05)SbO, and reduces to 0.02μB/Mn for (La0.95Ba0.05)(Zn0.95Mn0.05)SbO.On the other hand, as the ionic radius ofAEions increases, the Curie temperatureTCdecreases from~20 K for (La0.95Ca0.05)(Zn0.95Mn0.05)SbO to 14 K for(La0.95Sr0.05)(Zn0.95Mn0.05)SbO, and no long-range ordering is formed in (La0.95Ba0.05)(Zn0.95Mn0.05)SbO.Furthermore,in the same 1111-type (La,Ba)(Zn,Mn)AsO MS, μSR measurements indicate that ferromagnetic ordering develops in the entire volume.[12]While for(La,Ba)(Zn,Mn)SbO,the ionic radius of Sb3-(2.45 ?A) is larger than that of As3-(2.22 ?A),which leads to the result that the bond length of Zn/Mn-Sb is larger than that of Zn/Mn-As.Therefore, the p-d hybridization in(La,Ba)(Zn,Mn)SbO is much weaker,which eventually develops into spin-glass ordering state.We should note that in both (La,Ba)(Zn,Mn)AsO and (La,Ba)(Zn,Mn)SbO, carriers are coming from the substitutions of Ba for La which takes place in the La-O layers.While in another 1111-type La(Zn,Mn,Cu)SbO compound,the substitutions of Mn and Cu for Zn are taking place in the same Zn-Sb layers where the holes induced by Cu substitutions for Zn mediate the magnetic moments arising from Mn substitutions for Zn.
To summarize, we successfully synthesized a new 1111-type bulk MS (La,Ba)(Zn,Mn)SbO.The DC magnetization measurements reveal that the ferromagnetic interactions increase initially and then decrease with more Mn atoms doping,and the coercive fieldHCis as high as~11500 Oe.According to the AC magnetic susceptibility measurements,the samples evolve into conventional spin-glass ordering state below the spin freezing temperatureTf.The negative magnetoresistanceMRforx=0.075 has reached-88% at 2 K under the applied field of 9 T.We note that spin-glass ground state is common in II-VI MSs, and not unusual in recent bulk form MSs with decoupled charge and spin doping.The reason is largely ascribed to the strength of magnetic interactions and the competition between the long-range indirect ferromagnetic interactions of remote spins and the short-range direct antiferromagnetic interactions of moments at the NN sites.To understand the general mechanism for the ferromagnetic ordering in all magnetic semiconductors,this physical phenomenon has to be considered as an important part for the whole picture.Our sample enriches the MS families and is helpful for searching new MS materials with highTC.Furthermore,(La,Ba)(Zn,Mn)SbO has the same ZrSiCuAs-type tetragonal structure and favorable lattice matching as Fe-based layered superconductor LaFeAsO,[29]and it is possible to benefit potential spintronics applications.
Acknowledgements
Project supported by the National Key Research and Development Program of China (Grant Nos.2022YFA1402701 and 2022YFA1403202), the National Natural Science Foundation of China (Grant No.12074333), and the Key Research and Development Program of Zhejiang Province,China(Grant No.2021C01002).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures

