Energy-distributable waterborne acoustic launcher for directional sensing
Tian Yang(楊天), Wenting Gao(高文婷), Shida Fan(范世達), Jie Ren(任捷), and Tianzhi Yang(楊天智),?
1School of Mechanical Engineering and Automation,Northeastern University,Shenyang 110819,China
2Center for Phononics and Thermal Energy Science,Shanghai Key Laboratory of Special Artificial Microstructure Materials and Technology,School of Physics Sciences and Engineering,Tongji University,Shanghai 200092,China
Keywords: underwater sound,acoustic sensing and acquisition,metamaterials
During the last decades, significant advances have been achieved in metasurfaces.[1-10]More recently, waterborne acoustic metasurfaces have received extensive interest.Exotic waterborne acoustic behaviors have been observed successively.[11,12]However, superdirectional underwater acoustic signal transmission remains a great challenge due to the strong fluid-solid interaction(FSI).Previous waterborne acoustic lens equipment has many defects such as large acoustic beam side lobes and poor noise immunity.Hence,a novel device that can overcome the drawbacks of traditional underwater acoustic techniques and the limitations of the FSI is urgently needed to be developed.In recent years,derived from research on condensed-matter physics,quantumlike effects in topological acoustic systems have been widely noticed,[13-18]such as acoustic spin.[18-21]Many exotic acoustic behaviors can be predicted to depend on the distribution of acoustic spin.In addition, superdirectional airborne and waterborne acoustic transmission which overcome the limitations of beamwidth and effective frequency range have been realized recently.[7,22,23]However,waterborne acoustic power distribution and the prediction of superdirectional behavior still need further discussion based on waterborne phononic crystals(PCs).
In this paper, we apply a design of the valley-hall topology insulator (VHTI) to underwater acoustic communication and propose a directional waterborne topology acoustic launcher (WTAL) with an energy distribution function as shown in Fig.1.[16,24-26]Unlike airborne environments, the FSI is significantly evident in water.To obtain a large relative elastic modulus of the unit cells against the FSI,stainless steel(ASTM 1045) was selected to build WTALs.The material properties of the unit cells are listed in Table 1.Emitted parallel needle-like acoustic beams are received only by target audiences.Remarkably,the width of the output path is so narrow that the signal is not leaked to non-target listeners.Furthermore, the acoustic spin angular momentum and energy flow distribution at different interfaces inside the phononic crystal are provided and they show tight coupling.Energy changes in different sound paths can be achieved by simply adjusting the internal structure of the WTALs.In this sense,superdirectional acoustic energy distribution can be achieved based on such a platform with multiple tunable sound channels.

Table 1.Material properties.
As the acoustic kagome lattice PnC shown in Fig.1,gray areas represent the topological order origin with theC3spatial symmetry.To induce the topological phase transition, theC6symmetry is reduced by modulating the hopping amplitudee.Here,the kagome lattices are constructed of the trimers where the lattice constanta= 30 mm, the edge length of strictly symmetric trimerb=19.9 mm,ande=0.9 mm.The model and simulations are performed by the finite element software COMSOL Multiphysics.In this regime, two different valley states of the acoustic trimer located at the topological order origin (rotation angleθ=0?) intersect at the Dirac point in Fig.2(a).To transform the topological modes and initiate edge states,lattice deformations are introduced to break theC6symmetry in time-reversal (TR) invariant systems.Specifically,two reversible topological phases are realized via rotating the acoustic trimers.As shown in Fig.2(a),similar to the energy band inversion effect, two opposite valley states take place,corresponding toθ=±30?, and the opening of the Dirac cone is observed.As a result of the topological transition in PnC withθ/=0?,a separated band gap of 26.3-30.3 kHz(the widening of the band gap is discussed in supplementary material I)appears at the corner of the first Brillouin zone(BZ).It is worth noting that the yellow curves corresponding to the two band gaps with the acoustic spine shape represent opposite topological characteristics.
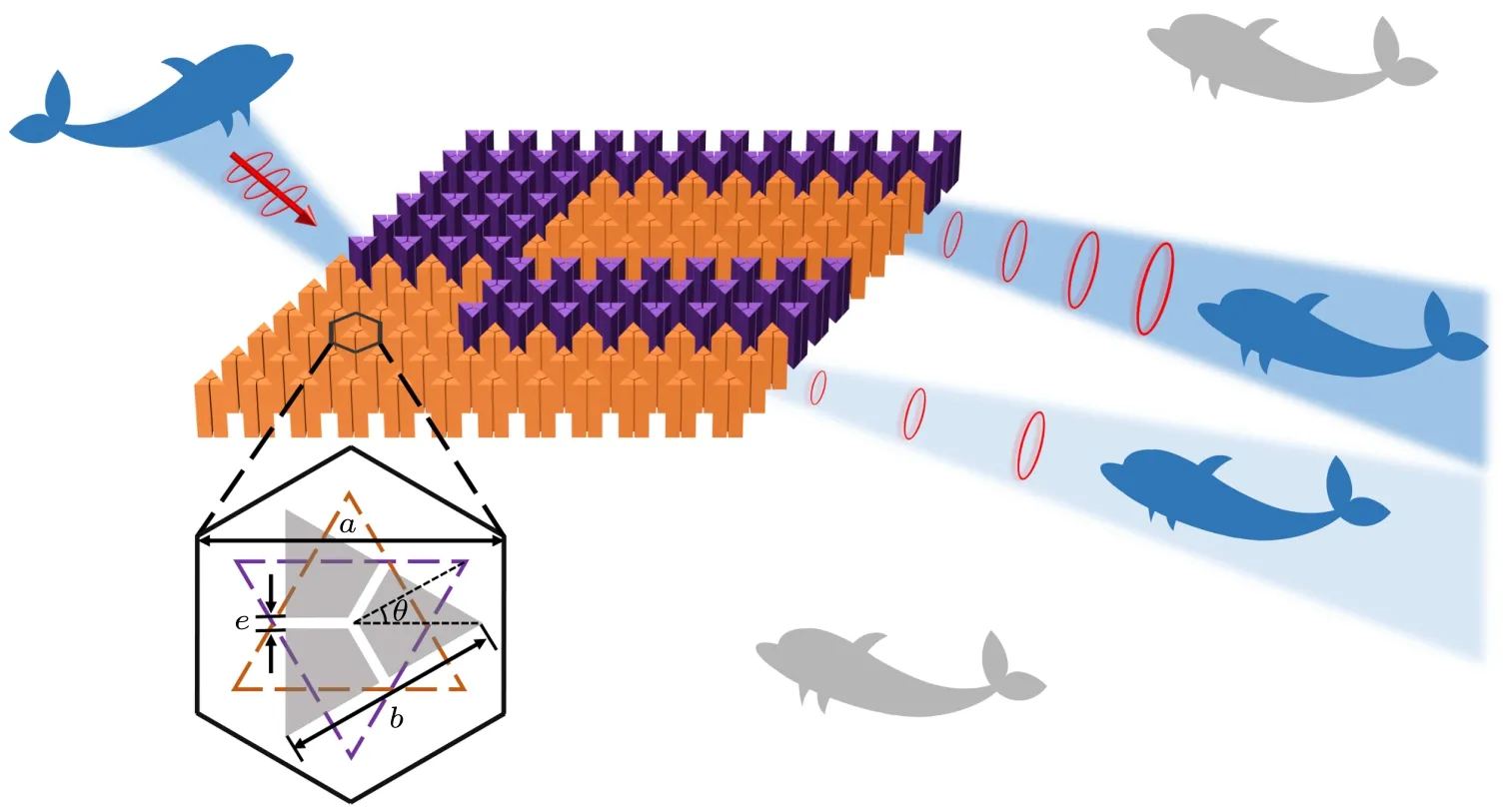
Fig.1.Schematic diagram of WTALs with an energy distribution function.The sound signal is focused on a target audience and cannot be leaked to undesired listeners.The energy of the sound signals focused on different target audiences is tunable.
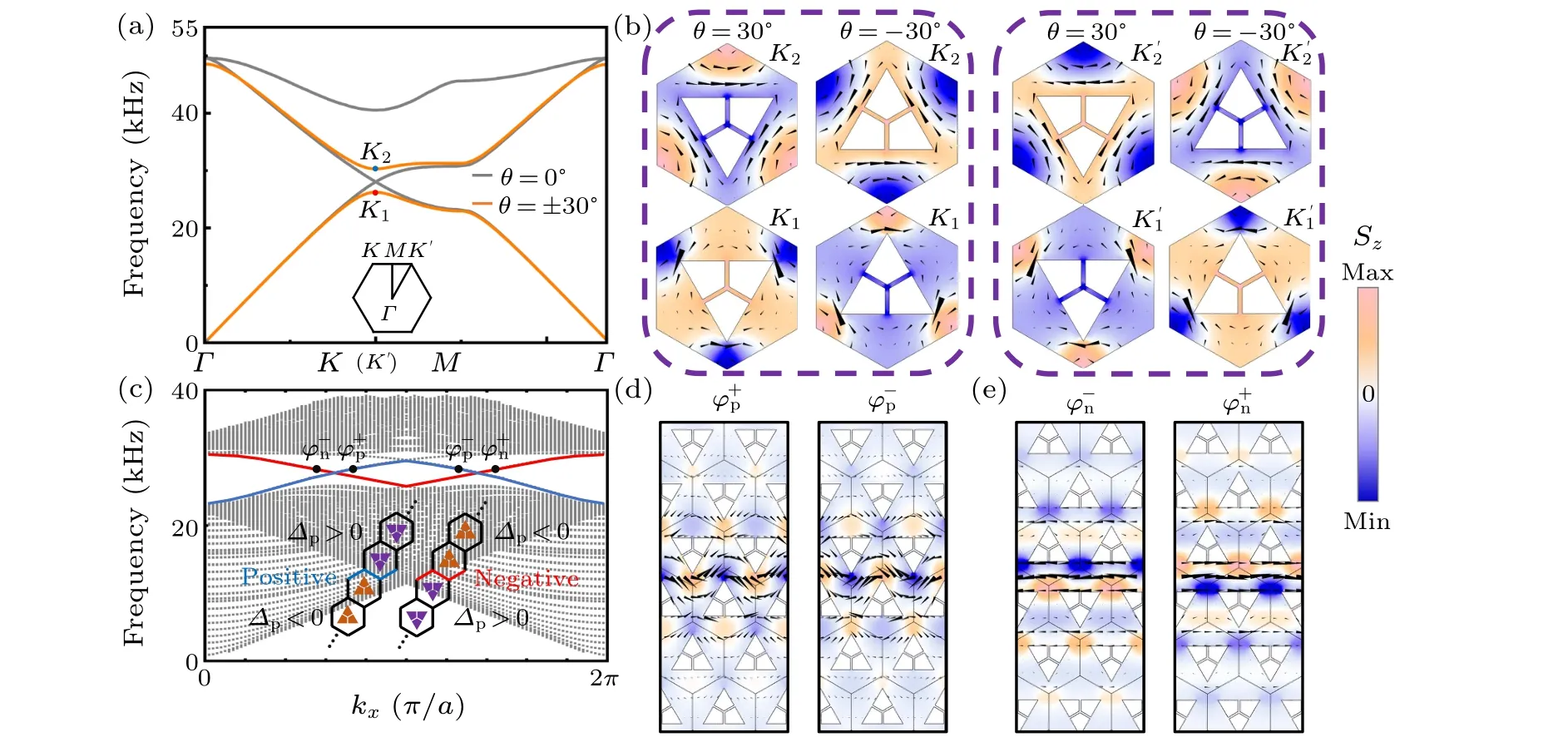
Fig.2.Band inversion and the acoustic spin mode of the acoustic trimers.(a)With the rotation angle θ =0?,a Dirac cone appears.The band inversion effect takes place with θ =±30?.(b)The color indicates distributions of acoustic spin normalized according to the maximum absolute acoustic spin at K and K′ points with θ =±30?.The unit of acoustic spin is kg·m-1·s-1.The black arrows represent the intensity and direction of energy flow.(c)Illustration of the dispersion relation of the superlattice.The blue(red)curve highlights the edge modes.Insets: the solid blue(red)line represents the positive-type(negative-type)interface.[(d),(e)]Illustrated distributions of energy flow and the acoustic spin normalized according to the maximum absolute acoustic spin at K and K′ points along the positive-and negative-type interfaces,respectively.
To illustrate the topological mechanism, the effective Hamiltonian and valley-Chern indices are provided according to the first-order Kadomtsev-Petviashvili perturbation theory.Specifically, subjected to the limited number of eigenmodes,H(k⊥)≡H(δk) =vD(δkxσx+δkyσy+mvDσz) is an approximation, andmis the effective mass defined asm=(ωk+1+ωk-2)/(2v2D), whereωkrepresents the band-edge frequency.[23]It is valid only in close proximity to the highsymmetryKandK′points of the BZ, wherevDis the group velocity,σi(i=x,y,z) are Pauli matrices of the valley states as the orbital degree of freedom, andδkis the distance from the Dirac points to theK(K′) points, respectively.[27,28]By considering the TR symmetry, the effective Hamiltonian in the inequivalentK′point can be derived directly asH(δk′)=vD(-δkxσx+δkyσy+mvDσz).The sign of the geometrical perturbation?pis determined by the rotation angle of acoustic trimers.In other words,?p< 0 (?p>0) corresponds toθ=-30?(30?).Furthermore, the non-vanishing valley-Chern indices can be expressed as 2C=±1×sgn(?p).[25,26,29]Considering the FSI,a large relative bulk elastic modulus of a trimer should be obtained after perturbation.It means that a large difference in elastic modulus between trimers and water is established.Otherwise, the relative elastic modulus of the trimers(e.g.,resins,etc.) is so small that no topological band gap appears.
In Fig.2(b), the acoustic spin distribution for all modes of the PCs are described.The acoustic spin can be quantitatively illustrated aswhereρis the mass density,ωis the frequency,νis the particle vibration(acoustic)velocity, andν?is the conjugate ofν.Here, the acoustic spin is a spatial distribution rather than pure positive or negative values.In general, topological properties of the valley states at theKpoint are considered in focus, and the properties in the inequivalentK′point can be derived directly by considering the TR symmetry.The insets in Fig.2(b) illustrate the intensity of the energy flow and the distributions of the acoustic spin at the valley states.For the erected trimers in the lattice, the lower boundary state of the acoustic spin is marked asK1, and the higher boundary state is labeled asK2.For an upside-down lattice, the state of the acoustic spin is the opposite to that in erected lattice.This is the micrometric basis of acoustic topological valley transport at the interface between two VHTIs.As shown in Fig.2(c),the dispersion curves of both single ribbon-shaped superlattices separated by a zigzag interface are calculated.Notably,the zigzag interfaces are designed oppositely clearly.The positive-type(negative-type) interface is marked by a solid blue (red) line.As a key manifestation of the topological insulator,both spindependent one-way edge modes with opposite group velocities marked by blue and red lines are observed in the bulk band gap with the range from 26.3 kHz to 28.3 kHz.Figures 2(d) and 2(e)illustrate the distributions of the acoustic spin and energy flow in the positive-and negative-type interfaces.Obviously,the modes of different directions are of opposite acoustic spins in the acoustic spine interface, and the tight spin-momentum locking is observed in the topological system as previously verified in experiments.[20,21,30,31]Similar to the spin profile of the Gaussian beam of longitudinal acoustic wave,as shown in Ref.[17],the two sides of the acoustic beam transmitted along a zigzag interface have opposite spin distributions.Furthermore,the intensity of spin and energy density show a gradual debilitating trend on both sides.
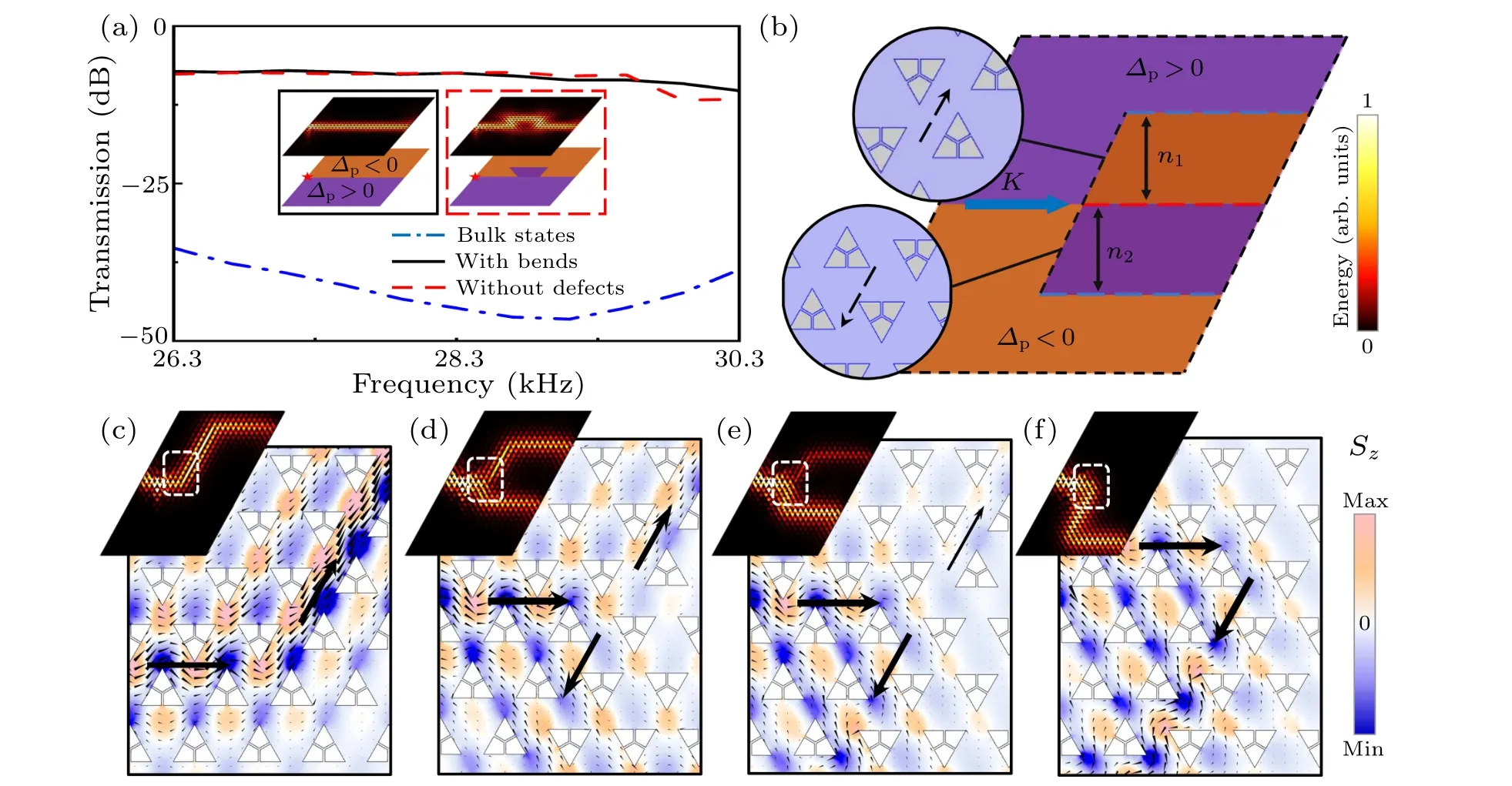
Fig.3.Topologically protected edge states at the positive-type interfaces with K′ valley polarization.(a)Transmission spectra of the topological valley transport with and without bends.Inset:simulated absolute pressure fields at the frequency f =28.3 kHz.The point source is located at the purple pentagram.(b)The model of WTAL with double positive-type interfaces.Blue dashed lines and red dashed lines represent positive-and negative-type interfaces,respectively.Here n1 and n2 indicate the number of rows of upside-down and erected trimers,respectively.The blue arrows represent acoustic transmission paths.Insets: details of the interfaces leading to the upper and lower sound paths.(c),(d),(e),(f)]Distributions of acoustic spin and energy flow at n1 =22(n2 =2),n1 =19(n2 =5),n1=12(n2=12),and n1=2(n2=22),respectively.
On the one hand, the launching and out-coupling of the valley-polarized edge states are the pivotal mechanism of WTALs inside the PCs.Local edge states out of the bulk band gap are supported at the interface between two valley-Hall PCs with different valley polarization.As shown in the inset of Fig.3(a), the topologically protected edge states of the straight and bent interfaces are observed.As an example,the two PCs are separated by a negative interface in a finite VHTI with 30a×30aunit cells.Only one valley polarized edge state propagates in the lock direction of the given valley, rested on an edge state atK′(K) point with ?C=-1(?C=1).Sound topological valley transport with remarkable immunity effect is localized at the proximity of the interface.High transmission of sound waves is sustained across the topological band gap.However, the bulk states disappear from the topological band gap and the transmission is measured below-30 dB as shown in Fig.3(a).Meanwhile,to observe the acoustic behavior of sound waves in multi-interface WTAL, two finite VHTIs connected in parallel at the right termination of the WTALs containing 60a×30aunit cells are established in Fig.3(b).Both VHTIs are composed of 20 columns andni(i=1,2) rows, whereniis natural numbers, andn1+n2=24.A sound point source at 28.3 kHz is launched along the positive-type interface projected from theK′valley.Obviously, the positive-type interfaces are located above and below the two VHTIs,respectively.However,they are separated by a negative-type interface.It means that sound waves projected along the positive-type interface from theK′valley cannot pass through the negative-type interface between VHTIs from left to right.By varyingn1andn2, the distribution shift of the normalized energy fields and the acoustic spin are shown in Figs.3(c)-3(f), sequentially.A clear and consistent variable trend of the acoustic spin and energy density is observed.It is noted that the types of interfaces leading to the upper and lower sound paths are different as shown in the insets of Fig.3(b).The interface of the downward sound path is perfectly matched to the initial interface, while the match of the upward sound path is so poor relatively that a higher impedance is exhibited.As a result,approximate equal distribution does not appear atn1=n2=12 in Fig.3(e) but takes place atn1=19(n2=5)in Fig.3(d).
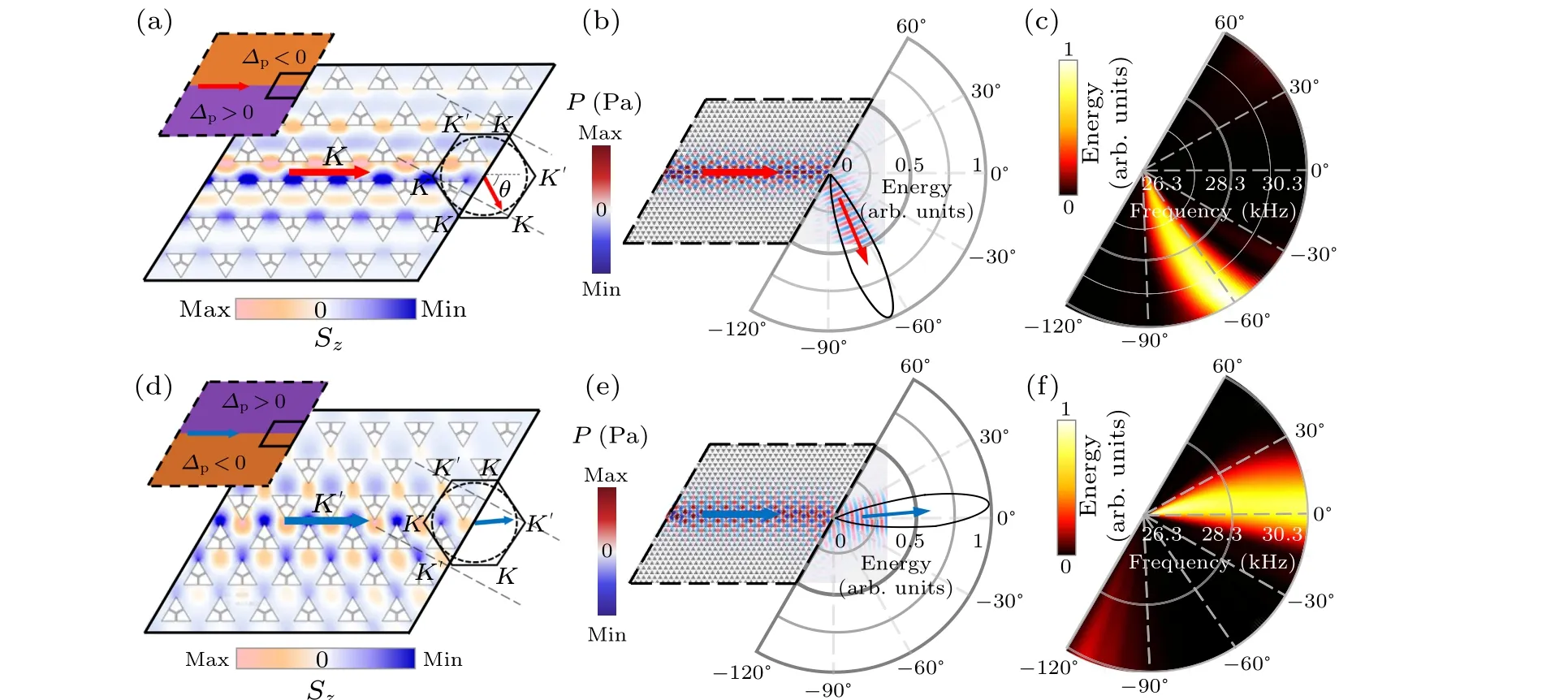
Fig.4.Superdirectional sound radiation of the WTALs.[(a), (d)] Distribution of acoustic spin corresponding to K and K′ valleyprojected along the negative-type (positive-type) interface in k space at f =28.3 kHz.A black solid hexagon indicates the 1st BZ and the black dashed circle represents the dispersion.[(b),(e)]Far-field distributions of normalized energy and sound pressure fields along the negative-type (positive-type) interface at f =28.3 kHz.[(c), (f)] Normalized acoustical energy spectra in the range of 26.3-30.3 kHz.
On the other hand, the acoustic energy launches into free space directionally along the positive-type and negativetype out-coupled interfaces of the WTALs as illustrated in Fig.4.The edge state guarantees reflection-free out-coupling which is essentially valley-projection.Moreover, whether inter-valley scattering is suppressed depends on the terminal type of the WTALs.A vanishing intervalley field overlap ensures that the undesired diffraction cannot take place at the zigzag termination of the WTALs.[26]Here, the radiation direction of the acoustic beam depends on the valley type of the projected edge state, which can be obtained according to the distribution of acoustic spin in Fig.2.As shown in Figs.4(a)and 4(d), the distribution of acoustic spin from left to right along the negative-type interface is consistent with the superlattice at?+pstate which is projected from theKvalley in Fig.2(d).It means that the negative-type interface corresponds to the excitation from theKvalley.Likewise, sound waves launched along the positive-type interface are projected from theK′valley.To obtain the refraction direction of the acoustic beam, the equifrequency curves in free space and the BZ are plotted on the acoustic spine scale.Along the direction parallel to the terminal of WTALs, the component of the incident wavevectorK(K′) is matched with the frequency curve in free space owing to the momentum conservation parallel to the WTALs boundary.Specifically, the refraction angle at the frequency 28.3 kHz can be calculatedLikewise, the refraction angle can also be determined to beθ+= 6.08?at the acoustic spine frequency for the WTALs with the positive-type interface.
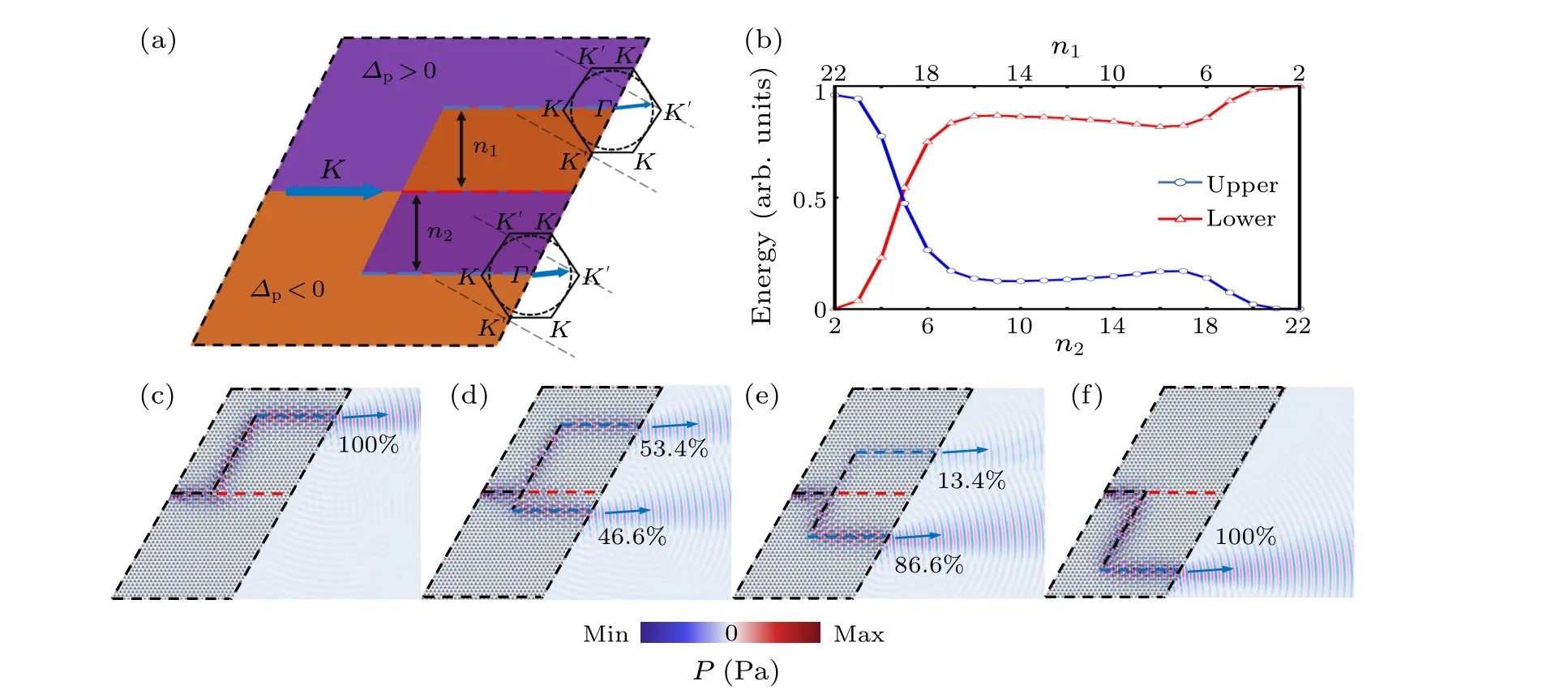
Fig.5.The model of WTAL with double positive-type interfaces.(a)Demonstration of superdirectional acoustic energy distribution with tunable WTALs.(b) Relationships between the normalized energy of the upper and lower paths and the number of rows of inverted and vertical trimers.[(c),(d),(e),(f)]Distributions of acoustic pressure fields at n1=22(n2=2),n1=19(n2=5),n1=12(n2=12),and n1=2(n2=22),respectively,and marked with the energy percentage in each sound path.
To verify the prediction of the theoretical refraction angles,the far-field radiation patterns of WTALs with negativeand positive-type interfaces are scanned within an angular range shown in Figs.4(b)and 4(e).The observedθ-=-66?andθ+=6?demonstrate indirectly that the out-coupled edge states obey the superdirectional selection rule of the valley projection.Positive (negative) angle acoustic refraction is completely suppressed by the WTAL with a negative-type(positive-type) interface.Furthermore, the far-field normalized energy spectra are observed across the entire frequency range of the topological band gap in Figs.4(c) and 4(f).It means that functions of the proposed WTALs can be implemented between 28.3 kHz and 30.3 kHz.Additionally, three remarks need to be clarified: (1) The theoretical predictions are in great agreement with the simulation results.The small angular difference originates from the detection step of 1?during the simulation.(2)The half-energy beamwidth of the main lobe of WTALs with negative(positive)interfaces is 20?(14?)without side lobes.Protected and efficient energy transfer ensures that the sound can be focused on the target audience without being compromised.(3) The peak amplitudes of the far-field radiation of WTALs are about 6.63 times than the standard acoustic waveguides.Considering thermal adhesion effect of acoustic structures,the actual gain should be reduced than theoretical gain as shown in supplementary material II.It implies that superdirectional transmission appears universally at considerable far-field sound levels.
Accurate superdirectional acoustic signal focusing not only is significant in underwater communication but also plays an important role in multi-channel acoustic information transmission.Considering both the internal and external characteristics of PCs, superdirectional acoustic energy distribution in parallel dual channels can be achieved with tunable WTALs in underwater acoustic environments.As illustrated in Fig.5, a sound point source at 28.3 kHz is launched along the positivetype interface projected from theK′valley as an example.The WTAL is acoustic spine as the one shown in Fig.3(b).As a result, parallel acoustic signals launched from the termination of the two positive-type interfaces can be obtained.Not only the two acoustic beams can be kept at a fixed interval relying onn1+n2=24, but their energy distribution will be achieved by rotating the unit cells in a whole row to varyn1andn2.Curves of the normalized energy distribution withniare shown in Fig.5(b).Specifically, the distribution of the sound pressure fields with the energy shift trend are shown in Figs.5(c)-5(f),sequentially.It is noted that equal distribution of energy does not take place atn1=n2=12 in Fig.5(e).As shown in the insets of Fig.5(a),the types of interfaces leading to the upper and lower sound paths are different.The interface of the downward sound path is perfectly matched to the initial interface,while the match of the upward sound path is so poor relatively that a higher impedance is exhibited.Thus,the intersection point of the energy distribution curve appears on one side instead of the middle in Fig.5(b), and approximate equal distribution of energy takes place atn1=19(n2=5)in Fig.5(d).Similarly, acoustic energy distribution can also be realized by launching along the negative-type interface projected from theKvalley.Rested on the above model, multichannel sound energy distribution at different intervals can be realized,depending on the requirements of the actual application.
In summary,we propose directional WTALs with an energy distribution function based on valley-hall topological insulators,which not only launch parallel needle-like signals in a specific direction but also control the energy of the acoustic signal from different sound paths.Unlike airborne environments, the FSI is significantly evident in water.To obtain a large relative elastic modulus of the trimers against the FSI,ASTM 1045 was selected to build WTALs.The distributions of angular momentum and energy flow in different cases are observed.Furthermore,high energy level communication is realized, relying on out-coupling and sustaining of valleypolarized edge states.WTALs can not only radiate superdirectional acoustic beams with a width of less than 20?but also adjust their energy.The theoretical predictions and simulation results are in good agreement.In addition, the equipment is expected to be further optimized towards miniaturization and broadbanding in the future.Superdirectional WTALs provide a desirable idea for high-energy-level directional collimated underwater sensing and underwater acoustic energy distribution.In this sense,multi-level directional acoustic energy distribution can be achieved potentially based on such a platform with multiple tunable sound channels.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos.12232014 and 12072221)and the Fundamental Research Funds for the Central Universities(Grant No.2013017).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures
- Improving dynamic characteristics for IGBTs by using interleaved trench gate

