Structural stability and ion migration of Li2MnO3 cathode material under high pressures
Ze-Ren Xie(謝澤仁), Si-Si Zhou(周思思), Bei-Bei He(賀貝貝), Huan-Wen Wang(王歡文),Yan-Sheng Gong(公衍生), Jun Jin(金俊), Xiang-Gong Zhang(張祥功), and Rui Wang(汪銳),?
1Faculty of Materials Science and Chemistry,China University of Geosciences,Wuhan 430074,China
2Wuhan Institute of Marine Electric Propulsion,Wuhan 430064,China
Keywords: lithium-ion battery,Li2MnO3,high pressure,DFT computation
1.Introduction
The ocean covers 70% of the Earth’s surface, and areas deeper than 103meters occupy more than 90%of the overall ocean area.The deep sea contains abundant oil,gas resources,and mineral resources.In order to develop these resources,new types of diving technology and equipment are required to meet the demands of deep-sea resource exploration.[1,2]In 2020, China sent a manned submersible, named “Striver”,into Earth’s deepest ocean trench.Lithium-ion batteries were chosen and used because of their high energy density, low self-discharge, and long life.[3-8]When used under such a condition, the electrode materials in the battery also experience enormous pressure.[9-12]Therefore, the properties of cathode materials under high pressure are worth studying.So far, the characteristics of LiCoO2,[13]LiFePO4,[14]and Li[Li1/3Ti5/3]O4[15]under high pressures have been studied.
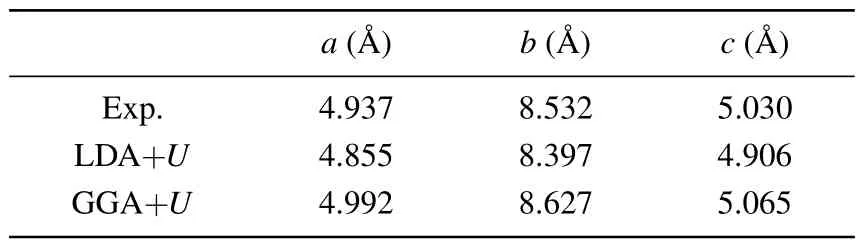
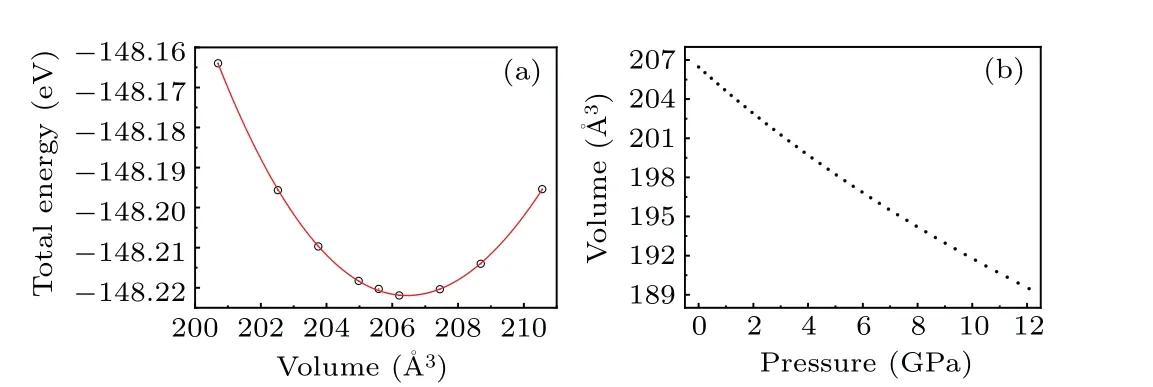
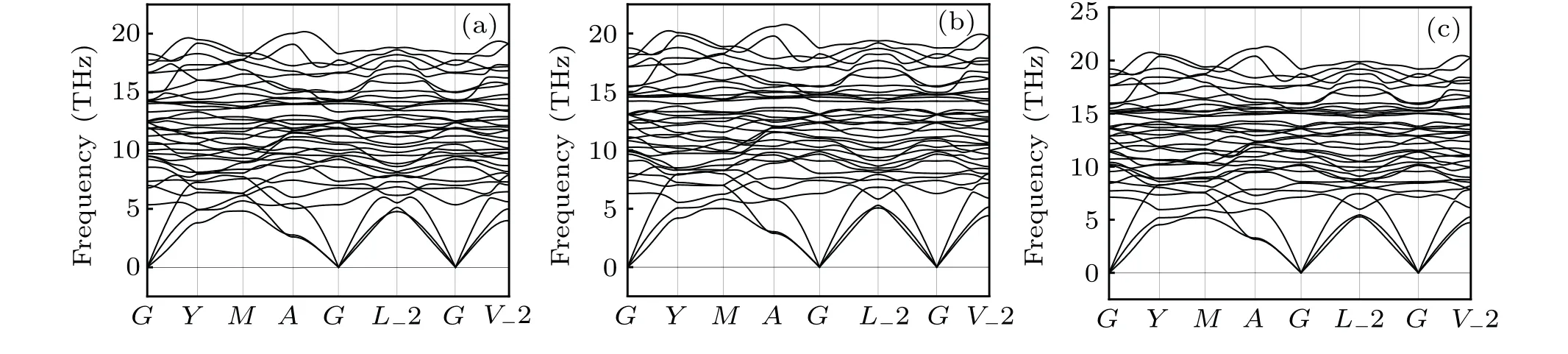
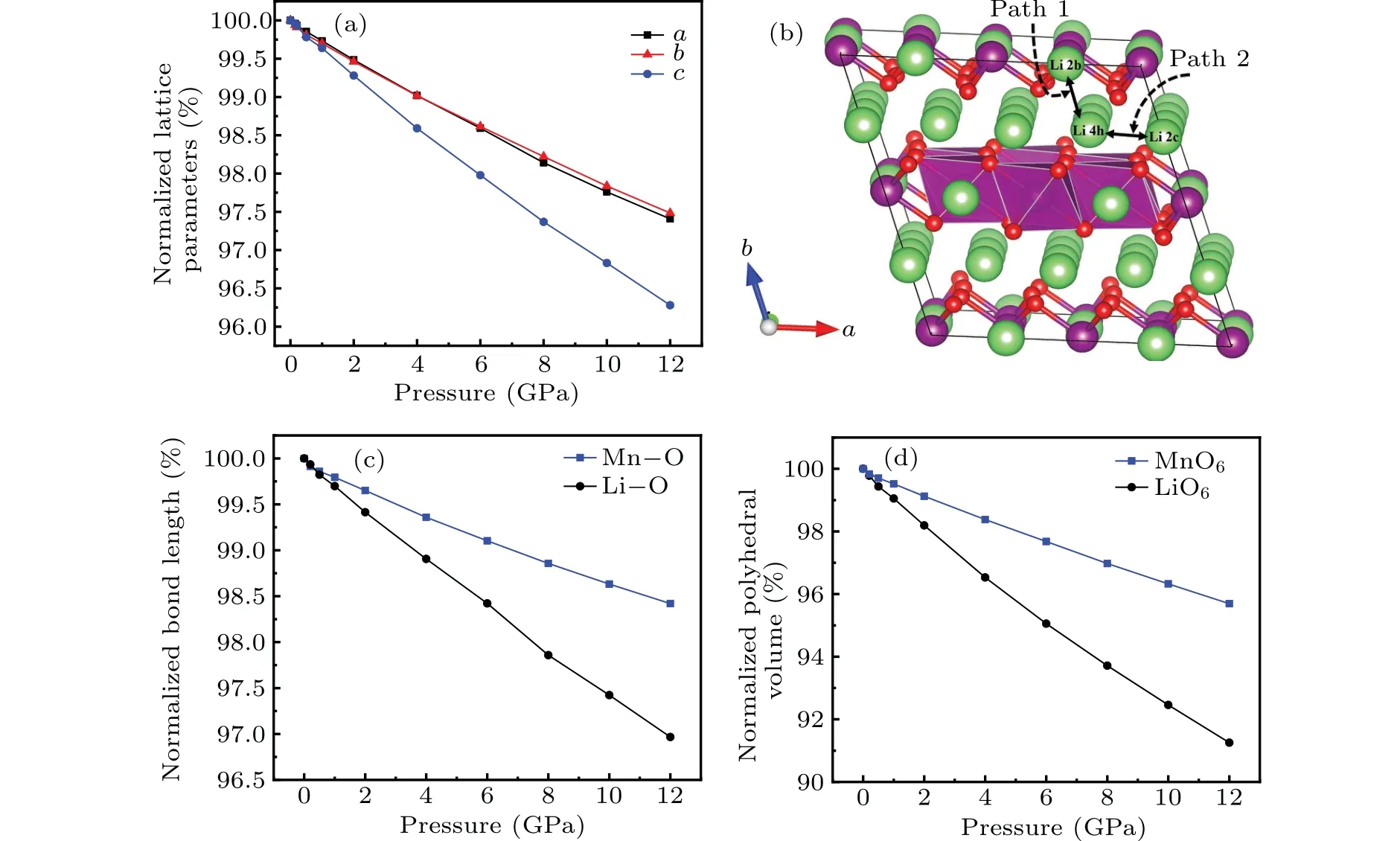
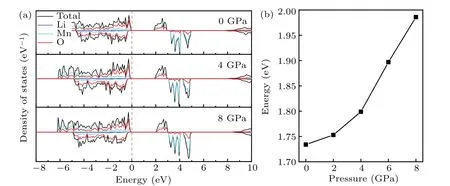
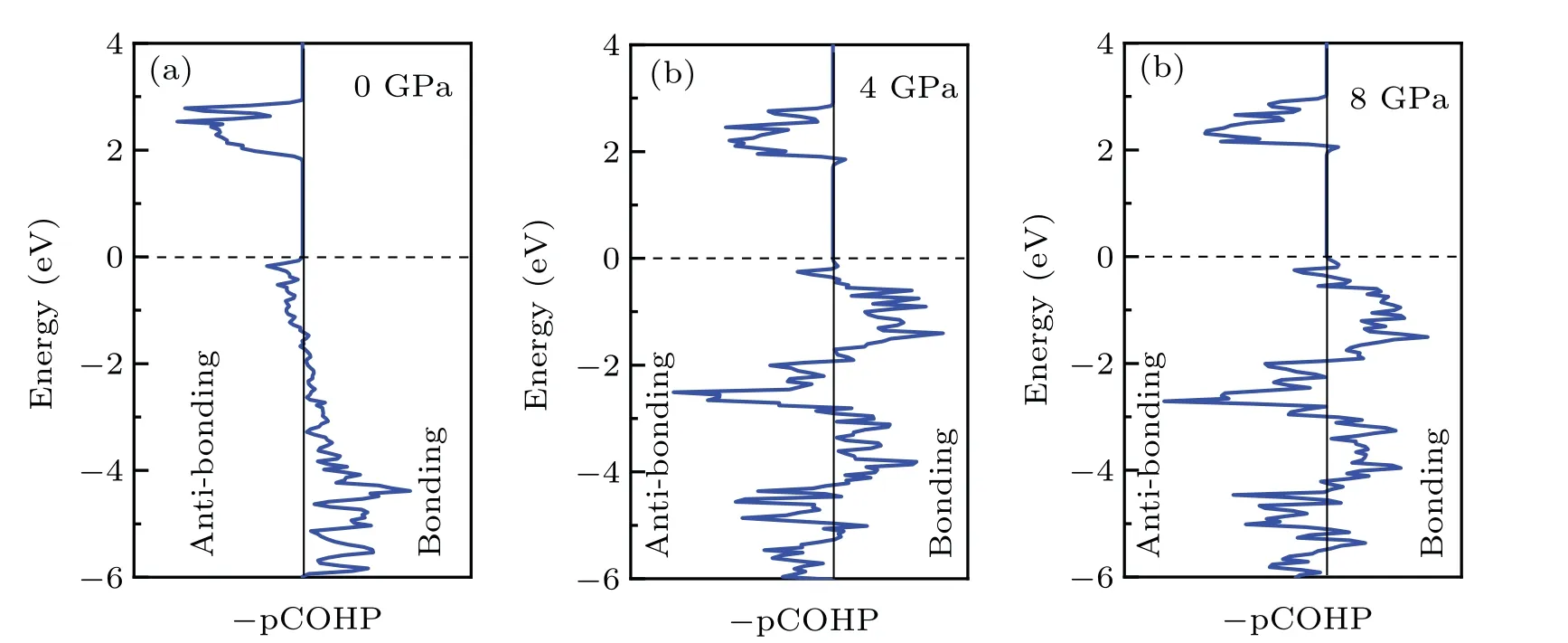
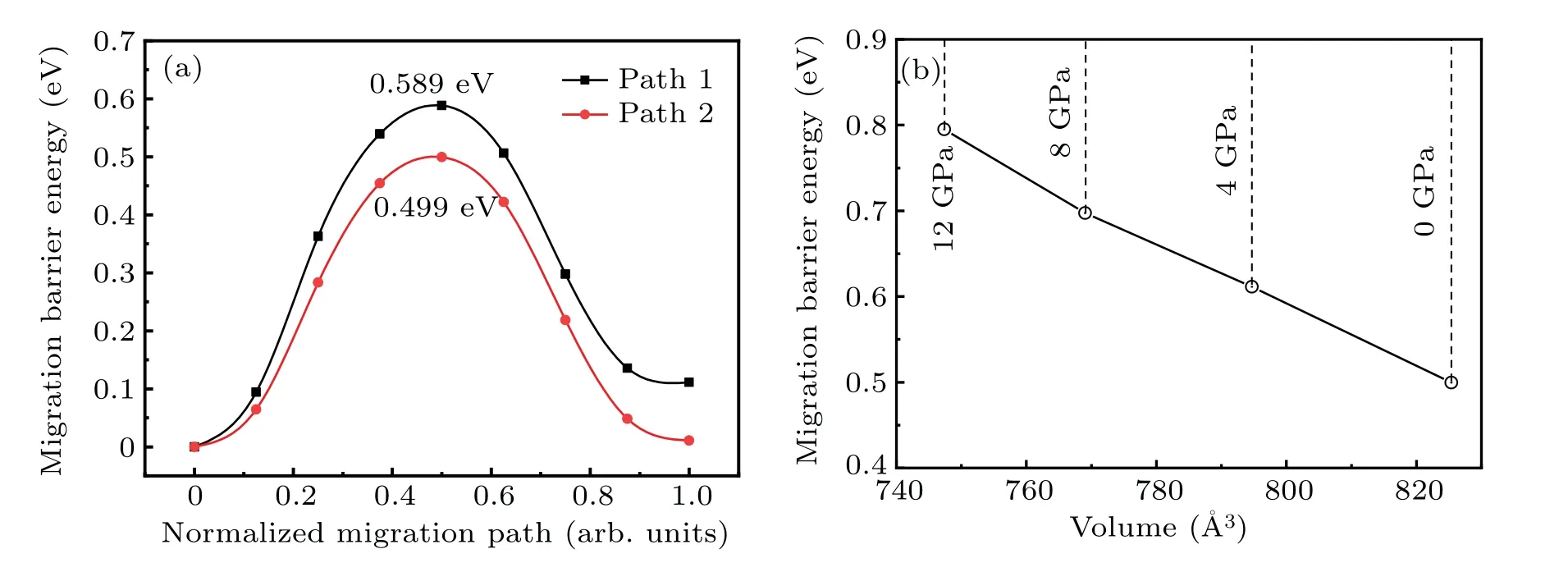
However, as the material with the highest energy density, the structural evolution and migration energy barrier of Li-excess Mn-based materials under high pressures are not yet clear.[16-19]The Li-excess Mn-based materials can be denoted asxLi2MnO3(1-x)LiMnO2(0 In this work,the equation of state,bulk modulus,steadystate volume,and migration energy barrier of LMO under high pressures are studied.It is reported that LMO still maintains a monoclinic phase at 12 GPa.[28]To avoid phase transition caused by pressure,[29]12 GPa was taken as the upper limit in this research. In this work, the Viennaab initiosimulation package(VASP[30])was used for spin-polarized density functional theory (DFT) calculations.The exchange-correlation function uses the Perdewe-Burkee-Ernzerhof (PBE) functional, and the electron-ion interaction is represented by the projector augmented wave (PAW) method.Considering the existence of strongly correlated electrons of Mn in Li2MnO3electrode materials, the method of GGA+U(U=3.9)[31,32]was used.In all calculations,the wave function had a plane wave cutoff energy of 600 eV.This set of parameters could make the residual stress between atoms in the optimized unit cell less than 0.01 eV·?A-1, and the total energy convergence threshold did not exceed 10-5eV.Relaxed structure calculations were performed at different constant volumes and the energy-volume data were fitted to a third-order Birch-Murnaghan equation of state(EOS):[33] The equation of state is a description of theP-Vstate relationship of a solid at constant temperature.TheE-Vequation(formula (1)) andP-Vequation (formula (2)) have the same four parameters,i.e.,E0(steady-state energy),V0(steady-state volume),B0(bulk elastic modulus), andB′1(first-order differential of elastic modulus to volume).By fitting theE-Vequation of the LMO,the relevant fitting parameters could be obtained to obtain theP-Vequation.The migration energy barriers of lithium ions in 2×2×1 supercell(96 atoms in total)were calculated by using the CINEB method,and the minimum energy for lithium-ion diffusion was obtained.Seven images were placed between the starting position and the ending position to simulate the process of lithium-ion migration. The calculation reproduces the monoclinic structure of the LMO(space groupC2/m),and the calculation method of LDA+Uis used to optimize the structure for comparisons.The cell parameter values and experimental values[34]of all optimized structures are shown in Table 1.The calculation results show that the cell parameter values obtained by using the GGA+Ucalculation method are close to the experimental values,and the same as other research results.[35,36] Table 1.Calculated and measured values of LMO cell parameters. The cell with optimized structure is adopted for calculation,and the third-order Birch-Murnaghan equation of state is used to fit the energy-volume diagram of the LMO as shown in Fig.1(a).According to the fitting results,the bulk modulus of LMO is 109.1 GPa and its first derivative is 4.9.At zero pressure, the equilibrium volume of the LMO is 206.46 ?A3.The pressure-volume relation of LMO within 12 GPa is shown in Fig.1(b).The prediction shows that at 12 GPa,the volume of LMO cell is about 189.5 ?A3, and the volume is compressed by about 8%,indicating that LMO is sensitive to high pressure environment. Fig.1.(a)The energy-volume relation and(b)pressure-volume relation calculated by LMO based on the third-order Birch-Murnaghan equation of state. The research results in Ref.[12]show that the LMO structure is still stable at 12 GPa under experimental conditions.Therefore, we performed phonon calculation for verification,and the results are shown in Fig.2.There is no imaginary frequency in the phonon spectrum calculated under each pressure,which indicates that the atomic vibration is stable under the corresponding pressures. Fig.2.Orbital overlap Hamiltonian population between Mn-O in LMO at 0 GPa(a),4 GPa(b),and 8 GPa(c). Figure 3(a)shows the variations of LMO cell parametersa,b, andcwith pressures.The results show that the lattice parameters decrease with pressure increasing.At 12 GPa,lattice parameters are 4.862 ?A, 8.410 ?A, and 4.876 ?A, respectively.After normalization, lattice parameters are reduced by 2.59%, 2.55%, and 3.72%.The compression rate of the cell is almost the same in the direction of [100] and [010], so it can be considered that the compression of the LMO in the direction of[100]and[010]are isotropic under high pressures.However, the compression ratio in the direction of [001] is significantly higher than the two pressures above: about 1.45 times the compression ratio in the direction of [010], which shows anisotropic compression.According to the LMO structure(Fig.3(b)),the layered structure of LMO in the direction[001]leads to large compressible space between layers. To further study the compression mechanism of LMO under high pressures, the compression of chemical bonds and polyhedra in the cell are compared.Figure 3(c)shows that Li-O bond is compressed by 3.03%at 12 GPa,while Mn-O bond is compressed by only 1.58%.Similarly,figure 3(d)shows the volume compression ratio of the polyhedron LiO6(8.74%)is significantly higher than that of MnO6(4.31%).Obviously,the calculation results indicate that the Li-O bond is easier to compress than the Mn-O bond, resulting in stronger compressibility of the octahedron LiO6, and the compression ratio in the direction of cell [001] is different from that in the direction of [100] and [010].Like the research results in Ref.[37],the higher the pressure,the more serious the deformation is.The migration of transition metal manganese ions to the lithium layer may also be related to the inconsistent compression ratio of the polyhedron. Fig.3.(a)Influence of pressure on LMO cell parameters,(b)LMO cell structure,(c)normalized bond length change of Li-O and Mn-O bonds with pressures,and(d)normalized volume of polyhedral LiO6 and MnO6 versus pressures. Figure 4 shows the calculated electronic structures of LMO under different pressures.When the pressures are 0 GPa,4 GPa,and 8 GPa,the band gaps are 1.734 eV,1.799 eV,and 1.986 eV,respectively.When the pressure is 0 GPa,the calculated band gap is consistent with related research result,[38,39]and with the gradual increase of pressure, the band gap begins to expand.This means that it is harder for electrons in the occupied state to transition to the unoccupied state,and the electrical conductivity of the electrons will gradually decrease.This can regulate the electrical properties of the material. In order to better expound the influence of pressure on the stability of the cell in terms of electronic structure, we calculate the projected crystal orbital Hamilton populations(pCOHPs)of Mn and O atoms under different pressures, and the results are shown in Fig.5.Figures 5(a)-5(c) show the-pCOHP graphs of LMO under 0 GPa,4 GPa,and 8 GPa,respectively.The integral of pCOHP(IpCOHP)is used to determine the influence of pressure on the stability of Mn-O bond.According to Fig.5(a), it can be found that at 0 GPa, there are some anti-bonding components in a range from-1.8 eV to 0 eV, and below-1.8 eV, bonding components are the main components.At this time,the stability of Mn-O bond is mainly contributed by bonding electrons.However, at 4 GPa and 8 GPa,it can be seen from the-pCOHP diagram that there are a large number of anti-bonding electrons below the fermi level,which reduces the stability of Mn-O bond.This is also illustrated in IpCOHP.The IpCOHP values at 0 GPa, 4 GPa,and 8 GPa are-2.12,-0.73,and-0.57,respectively,showing a gradually increasing trend.Therefore,pressure can affect the stability of Mn-O chemical bond in LMO cells to a certain extent. Fig.4.LMO electronic structure changing with energy at 0 GPa,4 GPa,and 8 GPa,respectively. Fig.5.pCOHP between Mn atom and O atom at 0 GPa(a),4 GPa(b),and 8 GPa(c),respectively. The CINEB method is used to calculate the migration path and migration energy barrier of Li+in LMO under highpressure compression,[40]and the ion migration paths are shown in Fig.3(b), where path 1 represents the migration of Li+at Wyckoff position 4h[41]in the lithium layers to site 2bin the transition metal layers, and path 2 represents the migration of Li+at site 4hin the lithium layer to site 2cin the lithium layer.At 0 GPa,the migration energy barrier of path 1 and path 2 are 0.589 eV and 0.499 eV,respectively,as shown in Fig.6(a).The calculation of the path 2 energy barrier is almost consistent with the related literature reports.The calculation results show that the Li+migration energy barrier height of path 1 is about 0.09 eV higher than that of path 2.Figure 6(a)also shows that the energy of Li+at site 2bis very higher than that at site 2c.This study indicates the huge difference in energy between the two paths from the perspective of energy,and Li+in the lithium layer is more prone to delithium. Fig.6.Migration barriers of different paths at 0 GPa(a)and(b)calculated variations of Li+ migration barrier energy with volume of path 2 under different pressures. Based on the calculation of diffusion path 2, we studied the influence of pressure on the diffusion energy barrier.The migration energy barrier of Li+increases from about 0.499 eV at 0 GPa(825.38 ?A3in volume)to nearly 0.795 eV at 12 GPa(747.37 ?A3in volume), and the change process is almost linear.This indicates that under the condition of cell compression,the ion migration channel will limit the migration of Li+,thus leading the ion conductivity to decrease.The decrease of ionic conductivity at high pressure makes LMO unsuitable as energy device for exploration in high-pressure environment such as deep sea or deep ground. The structural stability and electrical conductivity of Li2MnO3under high pressures are studied theoretically by using the first-principles calculations.The results show that the bulk modulus of the LMO is 109.1 GPa and the equilibrium volume is 206.46 ?A3.Under the same pressure,the compression rate of lattice parameters in the direction[100]and[010]are almost the same,but the compression rate of cell parameters in the direction[001]is obviously larger.The Li-O bond is more easily compressed than the Mn-O bond.The Li+at the 4hsite in the lithium layer at 12 GPa is more likely to migrate to the 2csite in the same lithium layer,and the diffusion energy barrier increases almost linearly with the increase of the pressure.These research deepens our understanding of the structural and electrical properties of layered Li-excess Li2MnO3under high pressures and can help us predict the effect of high voltage modification, which will provide useful information about the structural stability and conductive properties of cathode materials in the high pressure environment. Acknowledgement Project supported by the Research on High Power Flexible Battery in All Sea Depth,China(Grant No.2020-XXXXXX-246-00).2.Method
3.Results and discussion
3.1.Structural stability of Li2MnO3 under high pressures
3.2.Anisotropic compressibility of Li2MnO3 under highpressures
3.3.Electronic structure of Li2MnO3 under highpressures
3.4.Li-ion migration barrier energy of Li2MnO3 under high-pressures
4.Conclusions
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Improving dynamic characteristics for IGBTs by using interleaved trench gate

