王慧興(正高級教師 特級教師)

(清華大學(xué)附屬中學(xué))

1 知識要點

1.1 基本概念

以雙變量函數(shù)f(x,y)為例,給定x∈D1,當(dāng)y∈D2時,若f(x,y)有最大值M,則這個M與x的值有關(guān),是x∈D1的一個函數(shù)M＝M(x),再讓x∈D1,如果M存在最小值Mmin,則

通常稱之為一種復(fù)合最值,其中M稱為內(nèi)層最值,或“內(nèi)層最值函數(shù)”.復(fù)合最值也有其他形式,譬如

1.2 探求策略

探求復(fù)合最值的根本策略是基于內(nèi)層最值的概念,選擇數(shù)值或函數(shù)插值,組合常數(shù),按均值適度放縮,探求目標(biāo).

1.3 不可換序

復(fù)合最值與最值順序有關(guān),通常不可以交換.譬如根據(jù)函數(shù)圖像位置關(guān)系(如圖1),可得

圖1

2 典例精析

高校強基計劃校考筆試經(jīng)常立意復(fù)合最值試題,在高考試題中也多次出現(xiàn)復(fù)合最值試題.

2.1 基于內(nèi)層最值概念,構(gòu)建內(nèi)層最值函數(shù),轉(zhuǎn)化為單變量函數(shù),探求目標(biāo)

2.2 選定主元,辨別性質(zhì),合理定位,按均值放縮,探求目標(biāo)

探求一個復(fù)合最值,關(guān)鍵是基于內(nèi)層最值概念,先固定一個變量,以另一變量為主元,轉(zhuǎn)化成一個單變量函數(shù)M.根據(jù)這個單變量函數(shù)的特性——單調(diào)性與凹凸性,定位內(nèi)層最值,縮小包圍圈,建立內(nèi)層最值函數(shù)M.例1表明,這個內(nèi)層最值函數(shù)往往是分段的,這體現(xiàn)最值問題探究過程中的分類討論思想,這種分類討論常常可以通過“平均值組合”求解.

例2 同例1.

2.3 舍棄干擾項,合理取舍,組合常數(shù),按內(nèi)層最值與均值放縮,探求目標(biāo)

2.4 按內(nèi)層最值概念,均勻插值,化無限為有限

例6 (清華大學(xué))已知函數(shù)f(x)＝|x2＋a|＋|x|(x∈[－1,1]),記f(x)的最大值為M(a),求M(a)的最小值.

由對稱性,只需考慮x∈[0,1],由內(nèi)層取最大值,均勻插值,得

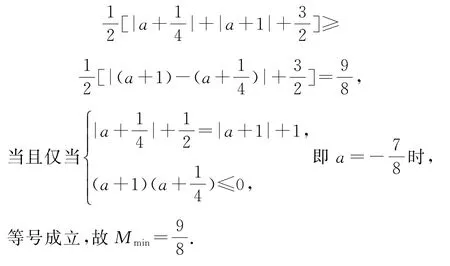
2.5 分析極端性,合理插值,化無限為有限

2.6 基于內(nèi)層最值布列不等式,按均值放縮,構(gòu)建目標(biāo)

例8 給定正數(shù)a,b,c,記,a＋b2＋c3}＝M,當(dāng)正數(shù)a,b,c變化時,求Mmin.

由內(nèi)層最值,得

解得M≤3,當(dāng)且僅當(dāng)時,有

2.7 綜合問題中的復(fù)合最值探求

2.8 探求組合問題中的復(fù)合最值

例11 10個人到書店買書,已知:

(1)每人都買了3本書;

(2)任何兩個人所買的書中,都至少有一種相同.

問:購買人數(shù)最多的一種書最少有多少人購買?

所以

即x≥4.如果x＝4,則所有xi＝4(i＝1,2,…,m),與矛盾,所以x≥5.

構(gòu)造:記Bi為互不相同的書,當(dāng)x＝5時,存在購買人數(shù)最多的一種書恰有5人購買的情況如下:

故購買人數(shù)最多的一種書最少有5個人購買.

2.9 應(yīng)用問題中的復(fù)合最值探求

例12 某企業(yè)接到生產(chǎn)3000臺某產(chǎn)品的A,B,C三種部件的訂單,每臺產(chǎn)品需要這三種部件的數(shù)量分別為2,2,1(單位:件).已知每個工人每天可生產(chǎn)A部件6件,或B部件3件,或C部件2件.該企業(yè)計劃安排200個工人分成三組分別生產(chǎn)這三種部件,生產(chǎn)B部件的人數(shù)與生產(chǎn)A部件的人數(shù)成正比,比例系數(shù)為k(k為正整數(shù)).

(1)設(shè)生產(chǎn)A部件的人數(shù)為x,分別寫出完成A,B,C三種部件生產(chǎn)需要的時間;

(2)假設(shè)這三種部件的生產(chǎn)同時開工,試確定正整數(shù)k的值,使完成訂單任務(wù)的時間最短,并給出時間最短時具體的人數(shù)分組方案.

(1)設(shè)完成A,B,C三種部件的生產(chǎn)任務(wù)需要的時間(單位:天)分別為T1(x),T2(x),T3(x),由題設(shè)有

其中x,kx,200－(1＋k)x均為1 到200 之間的正整數(shù).

(2)設(shè)完成訂單任務(wù)的時間為

3 實戰(zhàn)演練

(完)