橢圓中兩類三角形的內(nèi)切圓的性質(zhì)探究
2023-09-16 07:15廣東省中山市中山紀(jì)念中學(xué)528454謝林濤
中學(xué)數(shù)學(xué)研究(廣東) 2023年15期
廣東省中山市中山紀(jì)念中學(xué) (528454) 謝林濤
0. 準(zhǔn)備知識(shí)

1. 焦點(diǎn)三角形的性質(zhì)探究
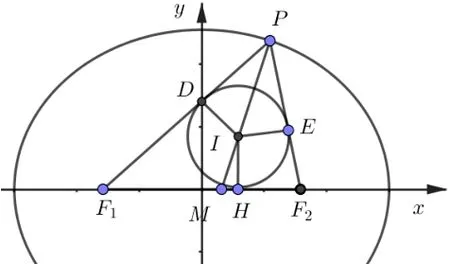
如圖, 橢圓C的標(biāo)準(zhǔn)方程為= 1(a>b>0),F1,F2分別為橢圓的左右焦點(diǎn),P為橢圓上不與左右頂點(diǎn)重合的任意一點(diǎn), ΔPF1F2的內(nèi)切圓圓心為I與ΔPF1F2相切于點(diǎn)D,E,H,PI與x軸交于點(diǎn)M(xM,yM),設(shè)點(diǎn)P(x0,y0),點(diǎn)I的坐標(biāo)為(xI,yI),則有如下性質(zhì):



2. 橢圓內(nèi)一類三角形的性質(zhì)探究
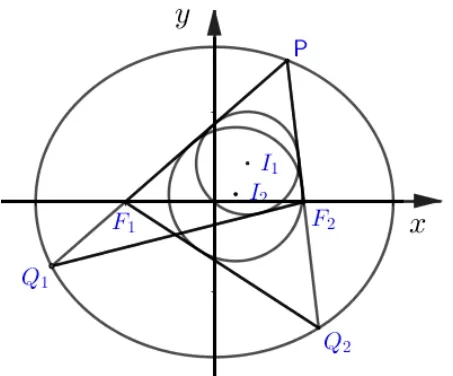
如圖2,橢圓C的標(biāo)準(zhǔn)方程為= 1(a>b>0),F1,F2分別為橢圓的左右焦點(diǎn),直線PQ1經(jīng)過點(diǎn)F1且與橢圓交于P,Q1兩點(diǎn),ΔPQ1F2的內(nèi)切圓圓心為I1, 半徑為r1, 直線PQ2經(jīng)過點(diǎn)F2且與橢圓交于P,Q2兩點(diǎn), ΔPQ2F1的內(nèi)切圓圓心為I2, 半徑為r2, 設(shè)P(x0,y0),Q1(x1,y1),Q2(x2,y2),直線PQ1傾斜角為θ1我們有如下性質(zhì):

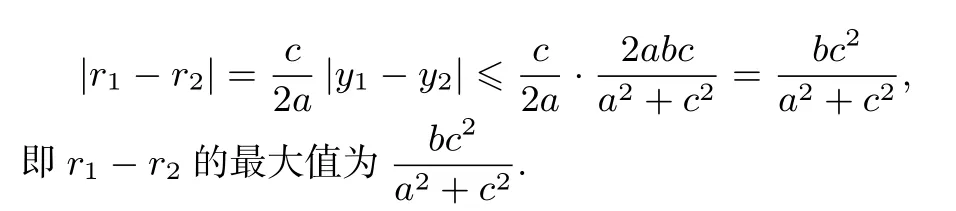
猜你喜歡
小資CHIC!ELEGANCE(2022年1期)2022-01-11
中等數(shù)學(xué)(2021年2期)2021-07-22
中等數(shù)學(xué)(2020年9期)2020-11-26
中等數(shù)學(xué)(2018年7期)2018-11-10
中等數(shù)學(xué)(2018年1期)2018-08-01
南方周末(2018-03-08)2018-03-08
中學(xué)數(shù)學(xué)雜志(高中版)(2018年1期)2018-01-27
科學(xué)中國(guó)人(2017年22期)2018-01-02
攝影之友(2016年8期)2016-05-14
數(shù)學(xué)教學(xué)通訊·初中版(2014年1期)2014-02-14

