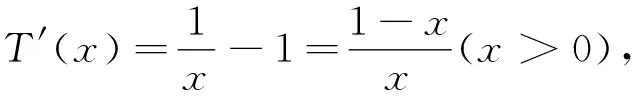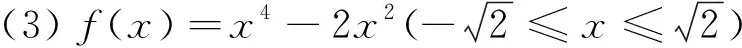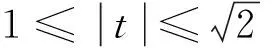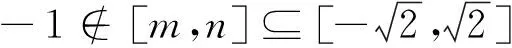江西省高安中學(xué) (330800) 朱細秀

2020年江蘇卷命制的函數(shù)綜合題考查內(nèi)容豐富,試題共設(shè)置了三小問,三小問中的函數(shù)各異,設(shè)問涵蓋了求函數(shù)解析式,參變量的取值范圍以及不等式的證明等眾多內(nèi)容, 要求考生熟練地掌握函數(shù)的圖像與性質(zhì),運用導(dǎo)數(shù)這一研究函數(shù)性質(zhì)的利器,以及數(shù)形結(jié)合、分類討論等眾多數(shù)學(xué)思想與方法才能順利地完成試題的求解,本文試對此作出評析.

試題已知關(guān)于x的函數(shù)y=f(x),y=g(x)與h(x)=kx+b(k,b∈R)在區(qū)間D上恒有f(x)≥h(x)≥g(x).

(1)若f(x)=x2+2x,g(x)=-x2+2x,D=(-∞,+∞),求h(x)的表達式;

(2)若f(x)=x2-x+1,g(x)=klnx,h(x)=kx-k,D=(0,+∞),求k的取值范圍;

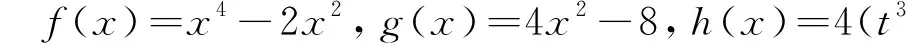
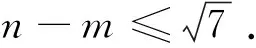
析解：(1)由f(x)≥h(x)≥g(x),說明等號也有成立的因素,故由x2+2x=-x2+2x,得x=0,則其中間函數(shù)h(x)滿足h(0)=0,所以b=0,又f′(x)=2x+2,g′(x)=-2x+2,所以g′(0)=f′(0)=2,所以h(x)=2x.由圖1可以看出,當h(x)=2x時,滿足要求.(實際上直線h(x)=2x在x=0處與兩函數(shù)f(x)=x2+2x,g(x)=-x2+2x圖像都相切,在區(qū)間(-∞,0)∪(0,+∞)上,f(x)=x2+2x圖像恒在h(x)=2x圖像上方,g(x)=-x2+2x圖像恒在h(x)=2x圖像下方.)

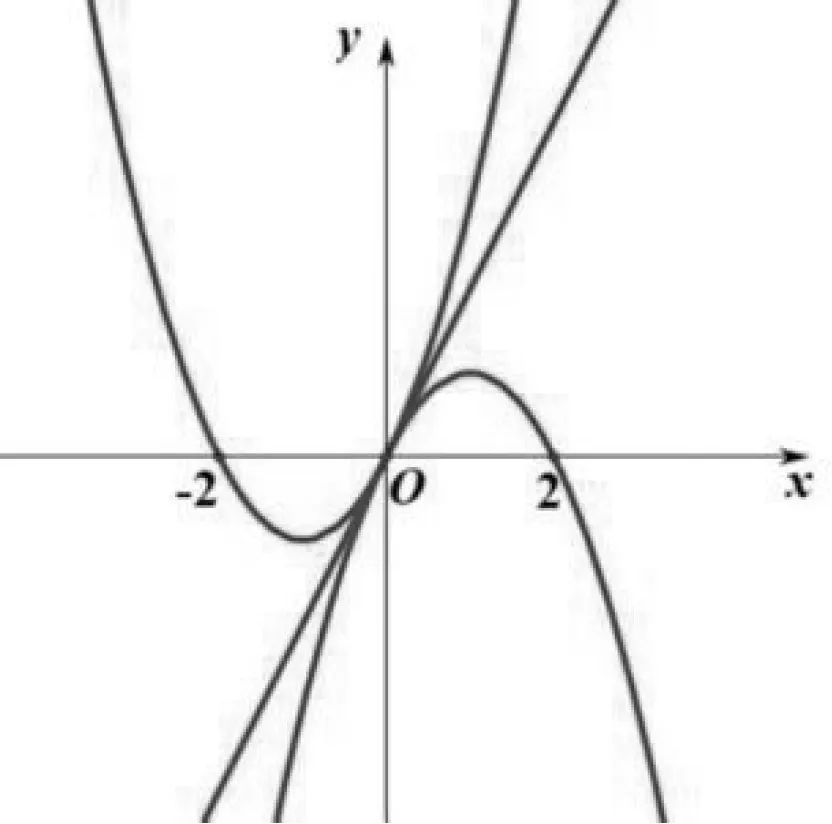
圖1