Danlei Chen ,Yiqing Luo, *,Xigang Yuan,2

1 School of Chemical Engineering and Technology,Tianjin University,Tianjin 300072,China

2 State Key Laboratory of Chemical Engineering,Tianjin University,Tianjin 300072,China

Keywords:Refrigeration system Optimal design Process systems Particle swarm optimization Mathematical modeling

ABSTRACT Simultaneous optimization of refrigeration system(RS)and its heat exchanger network (HEN)leads to a large-scale non-convex mixed-integer non-linear programming (MINLP) problem.Conventionally,researchers usually adopted simplifications to confine problem scale from being too large at the cost of reducing solution space.This study established an optimization framework for the simultaneous optimization of RS and HEN.Firstly,A more comprehensive and compact model was developed to guarantee a relatively complete solution space while reducing model scale as well as its solving difficulty.In this model,a tandem arrangement of connecting sub-coolers and expansion valves was considered in the superstructure;and the pressure/temperature levels were optimized as continuous variables.On this basis,we proposed a‘‘two-step transformation method” to equivalently transform the cross-level structure into a non-cross-level structure,and the de-redundant superstructure was established with ensuring comprehensiveness and rigor.Furthermore,the MINLP model was developed and solved by Particle Swarm Optimization algorithm.Finally,our methodology was validated to get better optimal results with less CPU time in two case studies,an ethylene RS in an existing plant and a reported propylene RS.

1.Introduction

Refrigeration system (RS) is a common operation unit in the process industry,which is mainly used as cold utility to provide cooling capacity for low-temperature process [1-3].As an energy intensive process with huge energy consumption,the problem of optimal synthesis of RS has gained increasing intension [4,5].For RS with multi-pressure/temperature levels,simultaneous synthesis with its corresponding heat exchanger network (HEN) plays an important role in improving the energy efficiency [6,7].Less energy consumption will lead to less burning of carbon containing fuels,less emission of greenhouse gas,thus benefiting the cleaner production and environmental sustainability.A single-stage vapor-compression RS [8,9],typically contains five basic components: condenser,expansion valve,evaporator,compressor,and sub-cooler.Herein,the sub-cooler is an energy-saving device,connected in front of the expansion valve,which can help lower the inlet temperature of the expansion valve,thereby reducing the exergy loss [10,11].

In practical industry,a RS works at multiple pressure/temperature levels and forms a complex HEN with process system.The RS and its HEN are highly inter-connected.Changes of RS structure(e.g.,the flow rate and temperature of refrigerant at each pressure-level) will affect heat transfer in HEN.Meanwhile,the fully thermally match of RS and process streams in HEN also needs adjustment of RS structure.Thus,simultaneous optimization of the HEN and RS is necessary to achieve better matches for heat transfer between RS and process streams,thus reducing energy consumption.Usually,it is a large-scale non-convex mixed-integer nonlinear programming (MINLP) problem for the simultaneous optimization of RS and HEN.The modeling solution of the large-scale non-convex MINLP problem is still a tough task,which can be divided into deterministic and stochastic approaches broadly[12].With respect to the former,there are several mature deterministic methods such as branch and bound technique [13],outer-approximation methods [14,15],branch and reduce algorithm [16],and extended cutting-plane methods [17] that have been used for solving MINLP problems.These deterministic methods converge quickly for small-scale convex problems and can guarantee a global optimal solution,but can be easy to fail to converge for large scale non-convex problems.With regard to the latter,stochastic algorithms are characterized by not relying on gradients and work based on the function evaluations alone.Group-based stochastic algorithms have obvious advantages in dealing with non-convex problems,such as the simulated annealing approach(SA)[18,19],genetic algorithm(GA)[20],and particle swarm optimization (PSO) [21,22].

Deterministic algorithms were mostly used for the problem of simultaneous optimization of RS and HEN.Simplifications were often made to confine the scale of the problem from being too large,and the simplified problem can be solved with the available methods.Based on an elementary multi-stage cycle superstructure,Shelton and Grossmann[23]proposed the first mathematical programming method with the temperature variables optimized as discretized variables,and developed a mixed-integer linear programming(MILP)model for a RS.They solved the model with standard branch and bound procedures (LINDO).Vaidyaraman and Maranas [24] added some potential devices to further develop the superstructure of RS,and solved their MILP model using CPLEX/GAMS.Wu and Zhu[25]introduced the sub-cooling process into the superstructure and proposed a MINLP model.However,when dealing with the simultaneous optimization problem,the process streams were preordained without being optimized.Through exergy analysis,Zhang and Xu [11] verified that adding sub-coolers would lead to the reduction of exergy loss at expansion valves,they solved their MINLP model with modified branch and bound technique (BARON/GAMS).However,they adopted fixed temperature levels in their model so that the corresponding HEN could not be optimized simultaneously.With the temperature variables optimized as discretized variables,Dinhet al.[10] constructed a superstructure with parallel expansion valves and subcoolers,and solved their MILP model with BARON solver.In our previous work [26,27],we introduced a tandem arrangement of connecting sub-coolers and expansion valves in the superstructure of RSs,which reduced the inlet temperatures of expansion valves,thus reducing exergy losses.The resulting uncertainty of intermediate variables was tackled by generalized disjunctive programming model.On this basis,an MINLP model was developed and solved with BARON solver.In our another previous work [28],we proposed a more comprehensive model for the synthesis of a RS with single refrigerant,along with optimizing the pressure/temperature levels as continuous variables.However,because of the difficulties in simultaneous solution of the large-scale problem by standard MINLP-solvers,a sequential optimization had to be performed.In general,when using the deterministic algorithm to solve the problem of simultaneous optimization of RS and HEN,simplifications were usually adopted,which may result in missing the global optimal solution.

Stochastic algorithm is an alternative method for the nonconvex large-scale MINLP problem.Wallerandet al.[29] proposed a bi-level solution strategy by combining deterministic and stochastic algorithm.In the master-level,all the temperature variables were optimized by GA;in the slave-level,other variables were optimized by CPLEX solver.By the strategy mentioned above,the large-scale problem was effectively solved,while the temperature levels were optimized within a preset range.It is well known that stochastic search strategy is very suitable for solving nonconvex MINLP problems,especially for high-dimensional and complex problems[12].PSO algorithm is a typical stochastic algorithm with fewer parameters,fast convergence and easy implementation.It has been widely used in the field of distillation sequence synthesis [30,31] and HEN synthesis optimization [32].

In this study,we proposed an optimization framework for simultaneous optimization of RS and HEN.Firstly,a comprehensive superstructure of RS was developed,in which a tandem connection of sub-coolers and expansion valves was considered and pressure/temperature levels were optimized as continuous variables.In this superstructure,when liquid refrigerant flowed from a higherpressure level to a lower one,it might lead to the cause of crosslevel structure,which was redundant and made the model complex and difficult to solve.Thus,then,a de-redundant non-crosslevel superstructure was established with reasonable redundancy removal while ensuring the comprehensiveness and rigor of the model.In this process,we proposed a ‘‘two-step transformation method” to equivalently transform the cross-level structure into a non-cross-level structure.Then,an MINLP model was developed based on the compact de-redundant superstructure.Next,the MINLP model was solved by PSO algorithm.Finally,the methodology proposed in this study was validated based on two case studies.One is an ethylene RS in an existing plant,the other is a reported propylene RS.

2.Problem Statement

In this problem,the detailed information of a set of process streams for the RS is given,such as the inlet/outlet temperature and the heating/cooling capacity.The objective of this study is to obtain an optimal RS with minimizing total compressor shaft work.Based on the de-redundant model,this problem will be solved to determine the basic structure,temperature levels,and flow rates.The assumptions of the problem are listed as follows:

i) The outflow of the refrigerant from compressors and the condenser are regarded as saturated vapor and saturated liquid,respectively;

ii) The number of pressure/temperature levels in this model is fixed due to the objective of minimizing total compressor shaft work.

iii) Heat capacityCptakes the average value over the entire temperature range,which does not vary with temperature.Saturated liquid enthalpyHcan be calculated by a linear correlation of temperature,which is regressed by simulated data from Aspen Plus (v11.0,by PR-BM property package).

3.Mathematical Model

3.1.Superstructure of RS

Fig.1 shows the superstructure of the RS with all possible connections among different levels.This superstructure hasMpressure/temperature levels (Mcould be any integer larger than 1).Each level contains an evaporator,a flash drum and a compressor.Besides,two adjacent or non-adjacent pressure levels can be connected by a tandem structure of connecting sub-coolers and expansion valves.Take the levelm(mcan be any integer between 0 andM) as an example,the liquid refrigerant from any higherpressure level (levelm′′) flows through the sub-cooler (CO-m′′m),and its temperature decreases before flowing into the expansion valve,where the liquid refrigerant is partially gasified due to the pressure drop.The refrigerant continues to be vaporized at a constant temperature by the evaporator (E-m) and absorbs the heat from process streams.Then the refrigerant flows into the flash drum(F-m) for gas-liquid separation.The liquid refrigerant enters a lower-pressure level (levelm′) to continue refrigeration process at a lower temperature,while the gas refrigerant enters the compressor (C-m) to be compressed level by level until back to the highest pressure (level 0).

The RS contains multiple pressure/temperature levels,which can provide cooling capacity at different temperatures.The liquid refrigerant from high-pressure levels flows through the tandem structure of connecting sub-coolers and expansion valves to lowpressure levels.As illustrated in Fig.1,the liquid refrigerant can either enter the adjacent low-pressure level (we call it the ‘‘noncross-level structure”) or cross it to a lower one (we call it the‘‘cross-level structure”).Considering the cross-level structure in the superstructure is undoubtedly comprehensive and rigorous,but it may also be redundant.This will introduce a large number of variables into the model,making it too complex to be solved.Therefore,some manipulations should be introduced to simply the model by reasonably removing redundant structures while ensuring the comprehensiveness and rigor.

3.2.Redundancy removal for the superstructure by the two-step transformation method

In this section,we proposed a ‘‘two-step transformation method” for the redundancy removal of the cross-level structure.Take the simple cross-level structure framed by the red square in Fig.2 as an example,for any two levels in the superstructure(levelsmandn) and their adjacent lower-pressure levels (levelsm+1 andn+1),there are not only non-cross-level streams,that are stream from levelsmtom+1 and stream from levelsnton+1,but also a cross-level stream,that is stream from levelsmton+1.

As shown in Fig.3,the cross-level structure can be equivalently transformed into a non-cross-level structure by two steps: 1) the cross-level stream(plotted in blue)is divided into a series of parts based on the number of levels it crosses,and each part is connected to the corresponding level forming a parallel structure of noncross-level streams;2) the parallel streams are merged and transformed into a simple non-cross-level structure.

Furthermore,as shown in Fig.4,there are two different ways of transformation according to the value ofTscm,n±1(the outlet temperature of the cross-level sub-cooler).For example,whenTscm,n+1is close to the temperature ofTn+1,as shown in Fig.4(a),only the sub-cooling part is divided;when theTscm,n+1is close toTm+1,as shown in Fig.4(b),only the pressure reduction part is divided;while other cases are in between.By the proposed‘‘two-step transformation method”,the cross-level structure can be equivalently transformed into a non-cross-level structure.

Through qualitative and quantitative analysis,it can be confirmed the rationality of the two-step method in the process of redundancy removal for cross-level structure.For qualitative analysis,the de-redundant non-cross-level structure has the same cooling capacity with the original cross-level structure.In the transformed non-cross-level structure,the original cross-level stream(stream from levelsmton+1)flows through each intermediate level (levelsm+1 ton) in turn and then enters the target level(leveln+1),although the flow rate of refrigerant in each level changes after transformation,the flow rate of effective refrigerant remains the same qualitatively.Here,the ‘‘effective refrigerant”means liquid refrigerant that is vaporized to provide cooling capacity at the evaporator of the particular level.For quantitative analysis,the compressor shaft work of the de-redundant non-cross-level structure is equal to that of the original cross-level structure.More details for the corresponding derivation process and case study validation can be seen in Supplementary Material,respectively.

3.3.MINLP model

After redundancy removal,a non-cross-level superstructure can be established for a RS with multiple pressure/temperature levels.On this basis,an MINLP model can be developed based on the following functions.

(i) Objective function: minimizing the total shaft work of the compressors;

(ii) Mass balance for each unit operation and stream mixing or split node;

(iii) Energy balance between refrigerant and process streams;

(iv) Equality and inequality constraints for the logical possibilities in the system.

3.3.1.Objective function

In this study,compressor shaft work was selected as the evaluation index of the RS.Therefore,the objective function is to minimize the total compressor shaft work as listed in Eq.(1).

whereWis the total compressor shaft work,Wmis the compressor shaft work of levelm,andSM={1,···,M} is the set of temperature levels.

The compressor shaft work of a single compressor at levelmcan be calculated by Eq.(2).

wherewfmis the specific shaft work of the compressor at levelm,fcmis the mass flow rate of the compressor at levelm.

Polytropic compression formula will be applied to calculate the specific shaft work (Eq.(3)) [33].

whereMris the molar mass of the refrigerant,mTis the polytropic exponent of compression,Zmis the average compressibility factor at levelm,Ris the molar gas constant,Tmis the temperature of levelm,Pmis the pressure of levelm,ηpis the polytropic efficiency of the compressors,ηmis the mechanical efficiency of the compressors.

3.3.2.Mass balance

Condenser

Mass balance for the condenser at level 0:

wherefc1is the outlet mass flow rate of the compressor at level 1,f0is the mass flow rate of level 0.

Sub-cooler

The liquid refrigerant stream at the sub-cooler of levelmcomes from the flash drum at the adjacent higher-pressure level(levelm-1).Eqs.(5) and (6) shows the mass balance at the sub-cooler.

wherefem-1is the liquid discharge flow rate from the flash drum at levelm-1,fxmis the flow rate at the sub-cooler at levelm,which is also the inlet flow rate of the flash drum at levelm,fe0is the liquid refrigerant from level 0.

Expansion valve

Due to the pressure drop,the refrigerant at the expansion valve of levelmis partially vaporized.The amount of gasification can be expressed by the gasification fraction,as shown in Eq.(7).

wherefvmis the flow rate of vapor (from expansion valve at levelm),vfmis the vapor fraction,which can be calculated by enthalpy balance.

Flash drum

After passing through the flash drum (levelm),the gas-phase and liquid-phase refrigerants are separated.The gas-phase refrigerant flows into the compressor.Then the liquid-phase refrigerant will flow into the adjacent lower-pressure level.Mass balance of the flash drum have been listed in Eqs.(8) and (9).

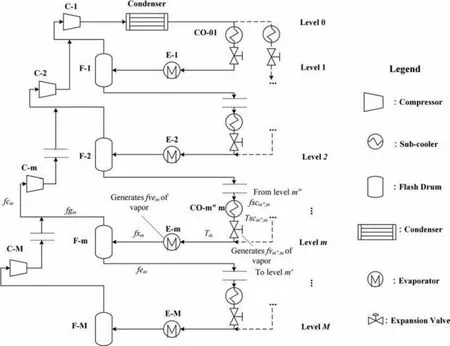
Fig.1.Superstructure of the RS.

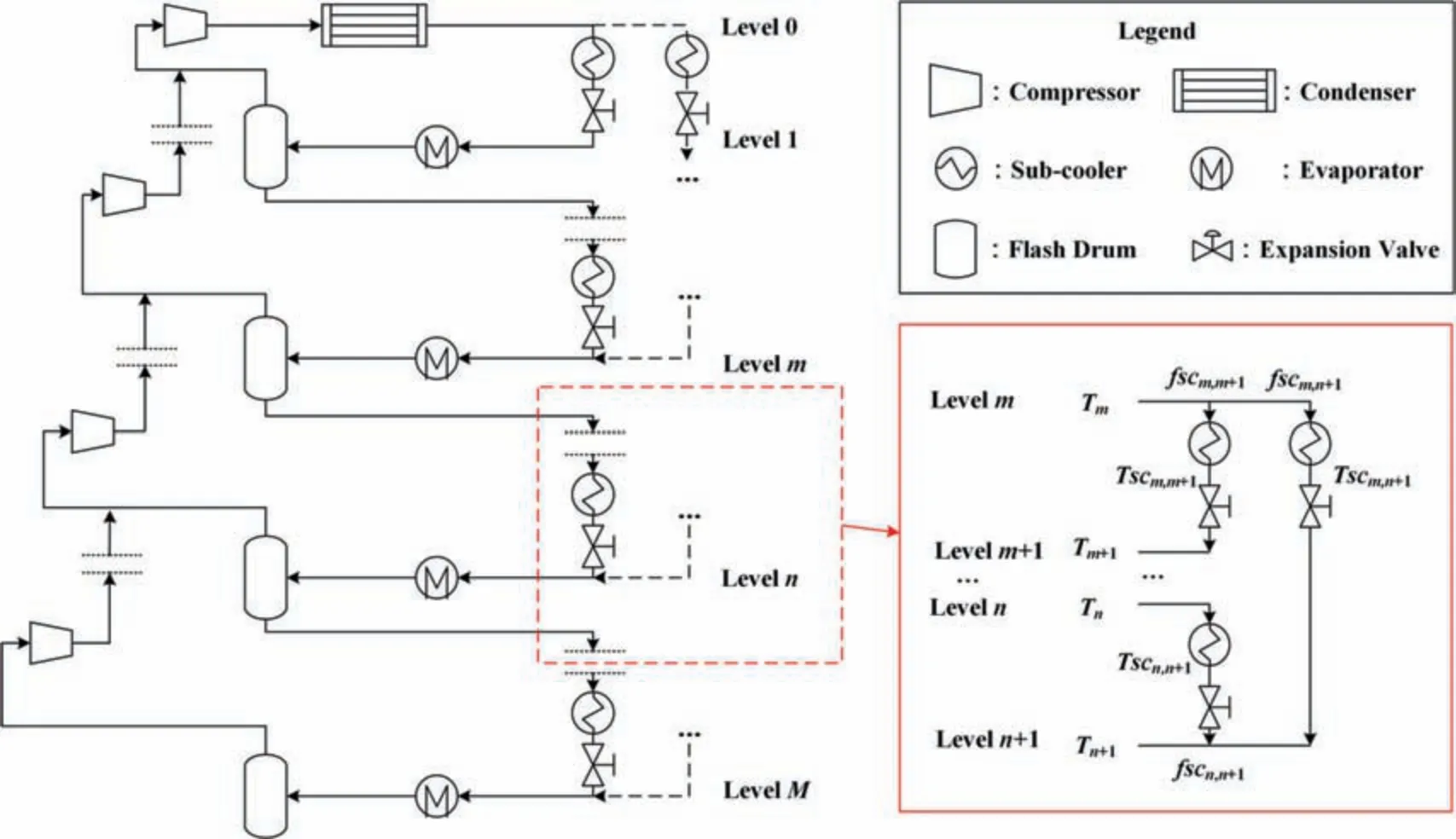
Fig.2.Diagram of a simple cross-level structure.

wherefgmis the mass flow rate of gas refrigerant from flash drum(levelm),femis the mass flow rate of liquid refrigerant from flash drum (levelm).

wherefvemis the amount of vaporization at the evaporator of levelm.

Compressor

The feed stream of the compressor at levelmconsists of two parts.One is the discharge stream of the compressor at the adjacent lower-pressure level (levelm+1).The other is the gas from the flash drum at levelm.Eq.(10) shows the mass balance of the compressor(levelm).In addition,the feed stream of the compressor at the highest-pressure level (levelM) only has one source,which is the vapor phase outflow of the flash drum (at levelM),as shown in Eq.(11).

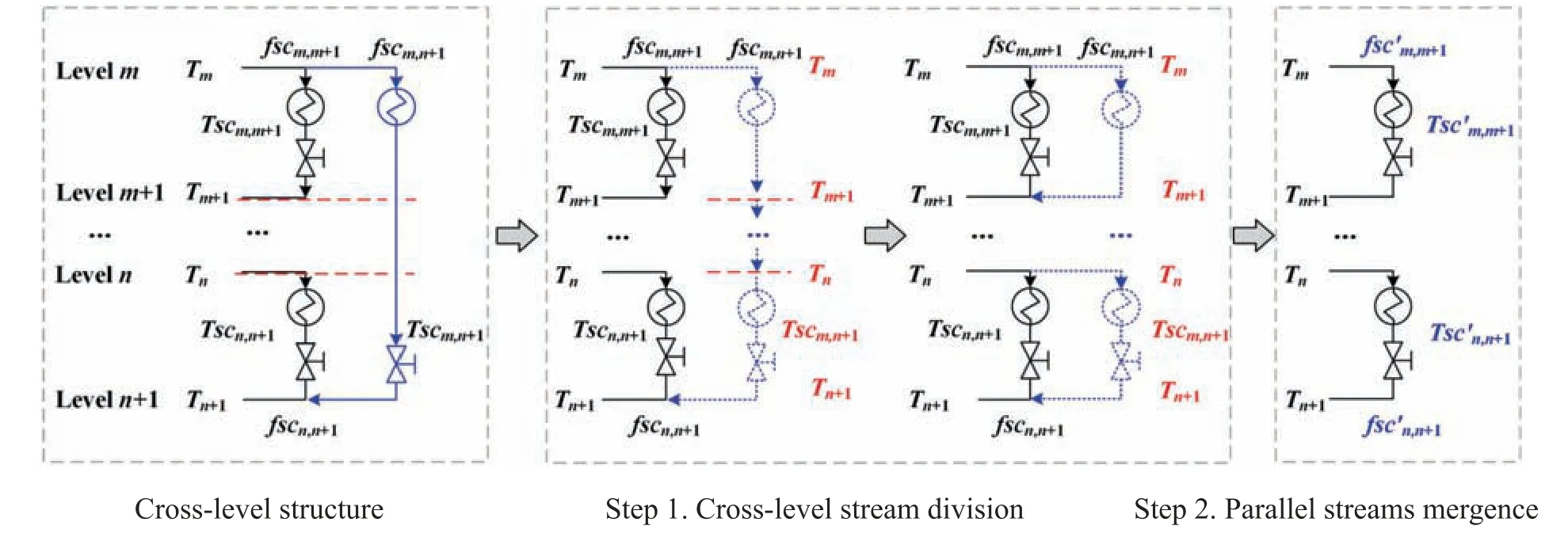
Fig.3.Diagram of the ‘‘two-step transformation method” for the cross-level structure.

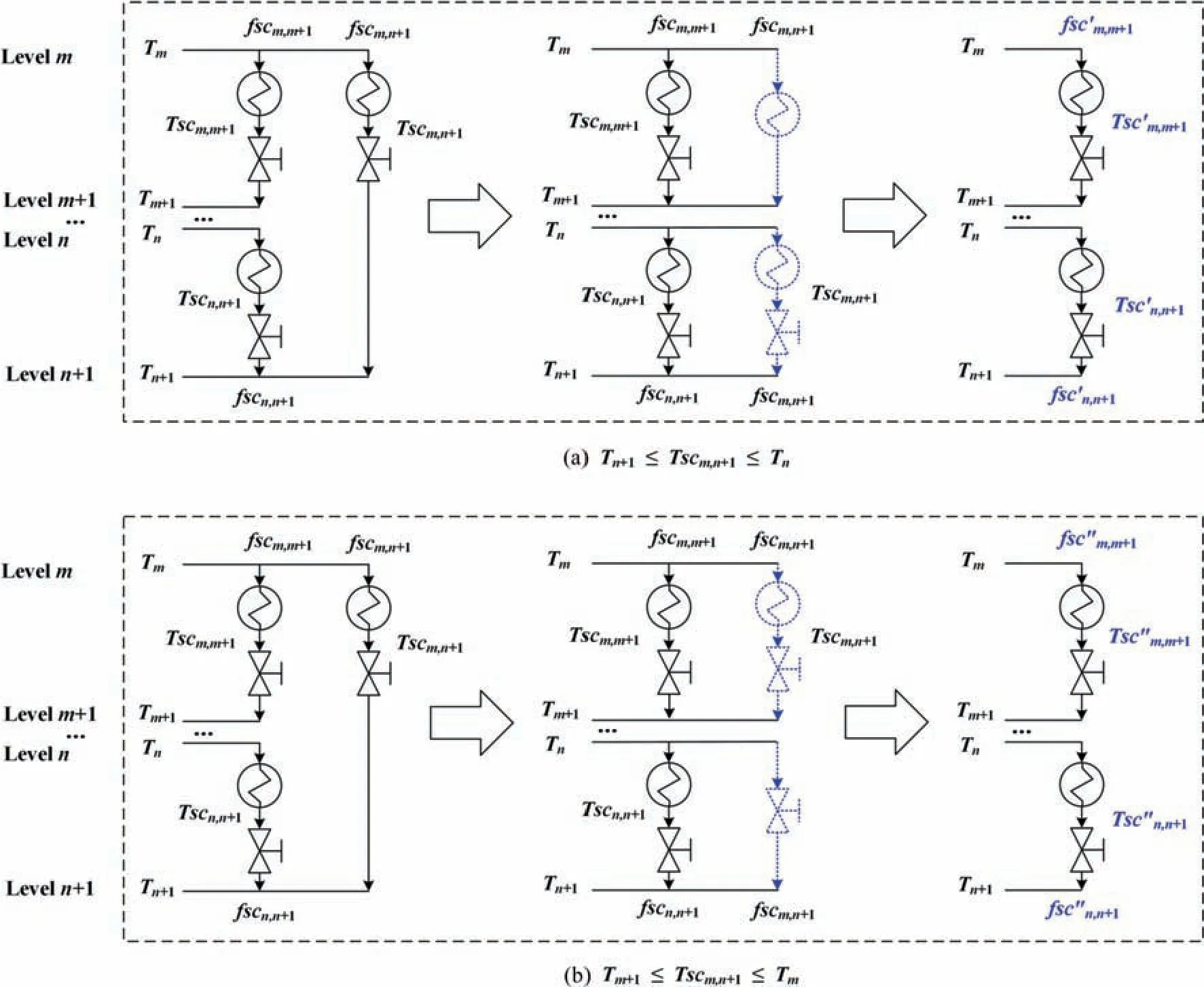
Fig.4.Two-step transformation method in two cases.

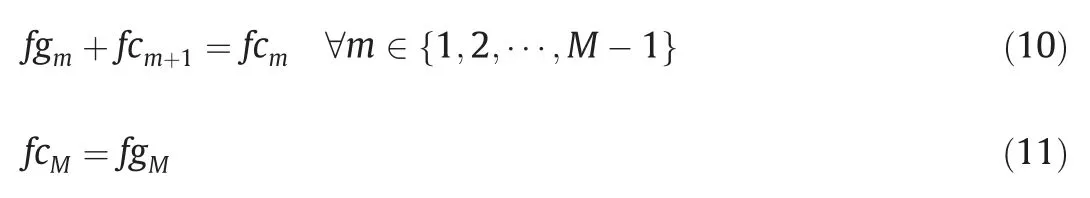
wherefcmis the mass flow rate of the compressor at levelm.

3.3.3.Energy balance

In this study,transshipment model[34]was used to express the heat balance of the system.The whole temperature range was divided into several temperature intervals according to the temperatures of the streams acting on the HEN,then the equation of heat balance was established in each interval.When setting the temperature intervals,all streams in the HEN were considered.Streams contain not only hot and cold streams,but also the refrigerant at sub-coolers and the refrigerant at evaporators in the system.Inlet temperatures and part of the outlet temperatures(which were above the maximum value or below the minimum value of the inlet temperatures) were listed as the potential temperature interval nodes.Then taking the temperatures of hot streams as the benchmark,adjusted all the temperatures,and ranked these temperatures in the descending order,then got the temperature intervals,calledST(ST={1,···,I}).Fig.5 shows the heat exchange in theithtemperature interval in HEN.This interval has three heat inlets,namely,heat from the hot process streams(QHi),heat generated by refrigerant at sub-coolers(UHi),and residual heat from the higher-temperature interval (Ri-1).It also has three heat outlets,namely,heat to the cold process streams (QCi),heat absorbed by refrigerant at evaporators(UCi),and residual heat to the lower-temperature interval (Ri).

Eq.(12) shows the heat balance expression in theithtemperature interval.

whereRiis the residual heat in theithtemperature interval,UHiis the heat provided by refrigerant in theithtemperature interval,UCiis the heat removed by refrigerant in theithtemperature interval,QHiis the heat provided by hot process streams in theithtemperature interval,QCiis the heat removed by cold process streams in theithtemperature interval.

Furtherly,the above heat balance (Eq.(12)) can be specifically expressed as Eq.(13).

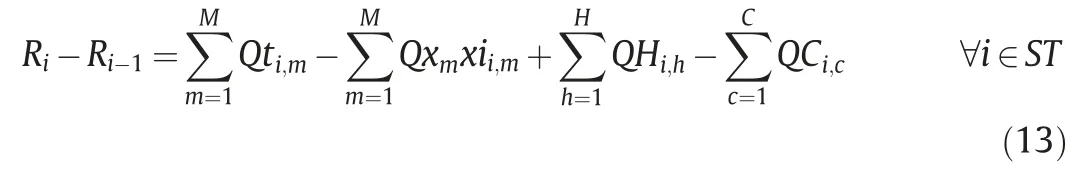
whereQti,mis the heat load of sub-coolers at levelmin theithtemperature interval,Qxi,mis the heat load of evaporators at levelmin theithtemperature interval,QHi,his the heat provided by thehthhot process stream in theithtemperature interval,QCi,cis the heat removed by thecthcold process stream in theithtemperature interval,xii,mis a binary variable,which is used to determine whether there is an evaporator in theithtemperature interval or not.

The heat duty of sub-coolers can be calculated by Eq.(14).

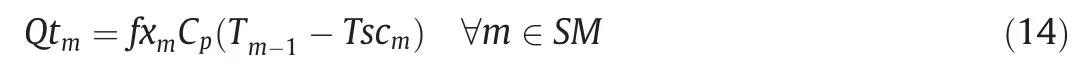
whereCpis the average heat capacity of the refrigerant,Tm-1is the temperature of levelm-1,Tscmis the outlet temperature of the subcooler at levelm.

Eq.(15) calculates the heat load of evaporators.

where Δhrmis the gasification latent heat of the refrigerant (levelm).

As confined by Eq.(16),all the residual heats should be nonnegative.In addition,the whole HEN is heat matched without external heat or cold supplement.Therefore,the net inlet and outlet heats of the HEN are 0,as shown in Eq.(17).

3.3.4.Other constraints

Except the above constraints,there are also some logical constraints in the optimal synthesis of the RS.Firstly,all the mass flow rate should be non-negative (Eq.(18)).Then,the outlet temperatures of the sub-coolers should be within the specified temperature range (Eq.(19)).Finally,as a closed system,the flash drum at the lowest-pressure level (levelM) has no liquid discharge (Eq.(20)).

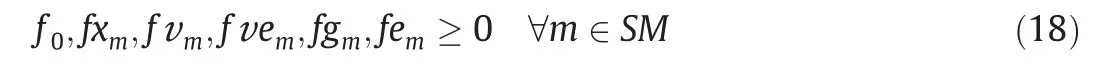
3.3.5.Summary of the MINLP model

The MINLP model for this study can be expressed as:minW=?m∈SM

s.t.Mass balance Eqs.(4)-(11).

Energy balance Eqs.(13)-(15).

Equality constraints Eqs.(17),(20).

Inequality constraints Eqs.(16),(18),(19).

There are some inequality constraints for this model.The whole model can be formulated as follows (Eq.(21)).minf（x）

Herein,x is a set of independent variables.Other dependent variables could be expressed by x according to the equality constraints,based on the reduced space algorithm [35].Note that the binary variablexii,m,which is used to determine whether the evaporator exists at a certain temperature interval in the transshipment model,is also related to x.This model could be reformulated as an unconstrained problem by exterior point method,see Eq.(22).

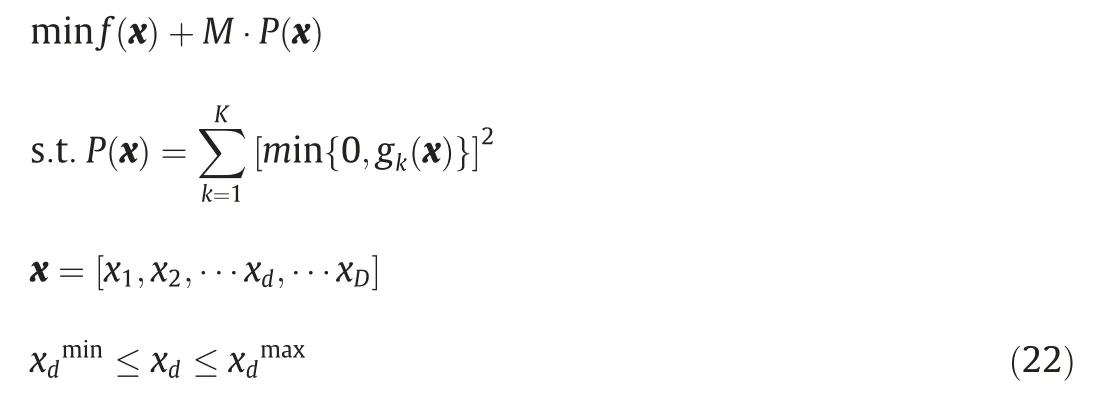
The MINLP model will be solved by PSO algorithm.

4.PSO Algorithm

PSO is a stochastic population-based optimization algorithm.Its structure is relatively simple.It is easy to be applied to various convex/nonconvex problems.The velocity update equation and position update equation of the standard PSO algorithm[21]are shown in Eqs.(23) and (24).

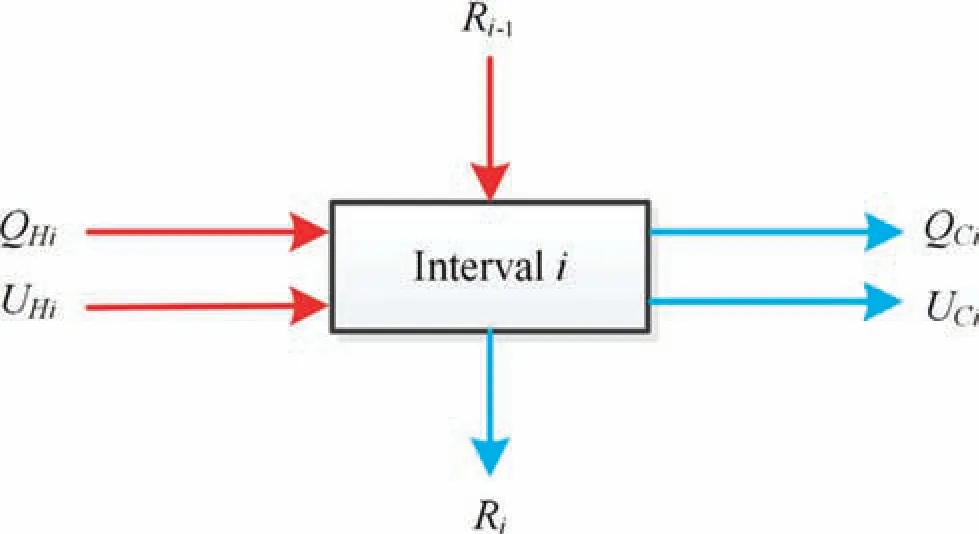
Fig.5.Schematic of the heat exchange in the ith temperature interval.

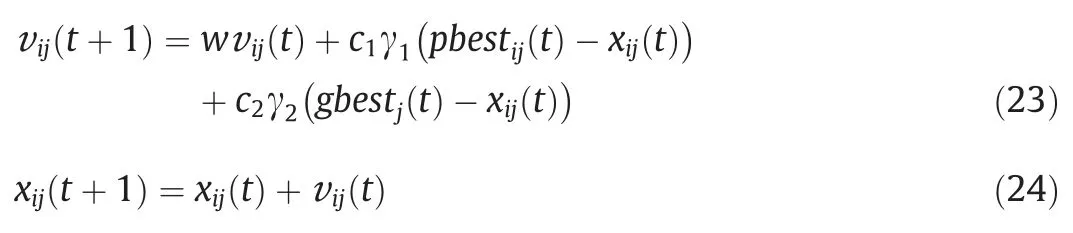
where v is the velocity of the particle,xis the position of the particle,tis the number of iterations,iis the number of the particles,jis the number of particle dimensions,wis the inertia weight,c1andc2are the acceleration constants,γ1and γ2are random numbers between 0 and 1,pbestij(t) is the best position searched by thei-th particle in thej-th dimension until thet-th iteration,gbestj(t)is the best position searched by all the particles in thej-th dimension until thet-th iteration.

Eq.(25) shows the equation of linear decreasing inertia weight(LDIW),which requires that the inertia weight linearly decreases with the increase of iteration times.Thus,the particle swarm can search extensively in the early stage of iteration,and converge as soon as possible in the later stage of iteration.

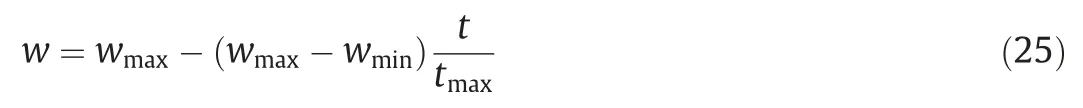
wherewmaxis the maximum inertia weight,wminis the minimum inertia weight,tmaxis the maximum number of iterations.

Fig.6 shows the optimization framework of PSO algorithm.For the large-scale MINLP problems in this study,the standard PSO has good performance.

5.Case Study

In this section,we conducted two case studies to verify the proposed model.One is an existing ethylene RS.The other is a propylene RS from the reported literature [10].For each case study,we constructed the cross-level model and non-cross-level model,respectively,and solved the two models by PSO algorithm.Then,we analyzed the optimal results.

5.1.Solution basis

The solution basis of the problem is summarized as follows:

(i) According to the industrial experience,the number of pressure/temperature levels (excluding the highest-pressure level) for the two case studies in our model were fixed as 3 for ethylene RS and 4 for propylene RS,respectively.

(ii) It is necessary to do the degree of freedom analysis to determine the number of independent variables,see Table 1.With respect to the Cross-level model,there are 3M2+13M+I+5 variables and 2M2+11M+I+5 equations,thus the degree of freedom of this model equals toM2+2M.With regard to the non-cross-level model,there are 14M+I+4 variables and 11M+I+4 equations,thus the degree of freedom of this model equals to 3M.Furthermore,the specific degree of freedom of the two models can be calculated when the number of levels (M) is determined.

(iii) When using the PSO algorithm,the population size was set as 10 times of the particle dimension (namely,the number of independent variables in the model).The inertia weight decreased linearly from 0.9 to 0.4.Two termination criterions worked together.The iteration of PSO algorithm would stop when it reached the maximum number of iterations(2000),or the fitness didn’t change (the gradient was less than 0.001%) over 100 epochs.Each model was tested for 100 times.For each test,it was considered to be successfully converged to the optimal result if the following relation holds good:

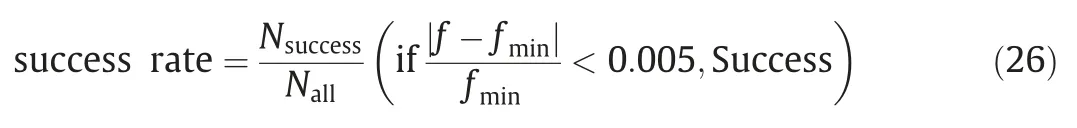
wherefis the solution obtained by the test,fminis the best solution in the 100 tests,Nsuccessis the number of successful tests,Nallis the number of tests.

In Table 1,f0is the total mass flow rate;fve1andfve2are the vapor produced by the evaporator at level 1 and 2,respectively;T0,T1,T2,T3,andT4are the temperature of the corresponding levels,respectively;Tsc0,1,Tsc0,2,Tsc0,3,Tsc0,4,Tsc1,2,Tsc1,3,Tsc1,4,Tsc2,3,Tsc2,4,Tsc3,4are the outlet temperatures of sub-coolers,respectively;x0,1,x0,2,x0,3,x1,2,x1,3,x2,3are the part of the flow fraction of the corresponding sub-cooler sections,respectively.

5.2.Case 1: retrofitting an ethylene RS in an ethylene plant

In this section,the existing ethylene RS was studied and applied to verify the proposed methodology and MINLP model.As shown in Fig.7,the studied system contains four pressure levels(16.45 bar,5.90 bar,2.16 bar and 0.13 bar,1 bar=0.1 MPa)and provides refrigerant at bubble point temperature of three lower pressures.The ethylene refrigerant at the highest-pressure level is condensed by propylene refrigerant(-39°C).This system provides cold duties for four hot streams (E-1 to E-4).In addition,this system also exchanges heat with three cold streams (CO-1 to CO-3).More details for the process streams can be seen inSupplementary Material(Table C-1).

We introduced two models to optimize the ethylene RS,i.e.,the cross-level model and the non-cross-level model,respectively.In each model,the independent variables were selected according to the degree of freedom,as shown in Table 1.Herein,the temperature at level 0(T0)was pre-fixed to-34°C,instead of being optimized.The temperature at level 3 (T3) was determined by the minimum outlet temperature of hot process streams,which was -98 °C.The minimum temperature approach in the HEN was set as 2°C,thusT3was-100°C.Both of the two models were solved by PSO algorithm.The structure of the optimal results is shown in Fig.8(a) and 8(b).

We have listed the optimal results of the ethylene case in Table 2.We have compared the total compressor shaft work (W)from the base case,the optimal result in our previous study [28]and the optimal results by PSO in this study.In our previous study[28],the MINLP model was solved by deterministic algorithm(BARON solver).Due to the difficulties in solving the large-scale non-convex problem by standard MINLP-solvers,a sequential optimization was performed,that could lead to the missing of the optimal solution.As listed in Table 2,the optimizedWobtained by PSO(cross-level 4493 kW,non-cross-level model 4487 kW)are smaller than that obtained by deterministic algorithm (4596 kW).Compared with the cross-level model,theWsaving by the non-crosslevel model is further increased (9.37%),with less CPU time(0.68 s) and greater success rate (approximately 100%).

5.3.Case 2: retrofitting a propylene RS in literature

As shown in the case study of Dinhet al.[10],the more complex propylene system contains five pressure levels (16.93 bar,10.81 bar,7.27 bar,3.73 bar and 1.43 bar)and provides refrigerant at bubble point temperature of four lower pressures.The propylene refrigerant at the highest-pressure level is condensed by cooling water.This system provides cold duties for twelve hot streams(E-1 to E-12).In addition,this system also exchanges heat with five cold streams (CO-1 to CO-5).More details for the process streams can be seen inSupplementary Material(Table C-1).

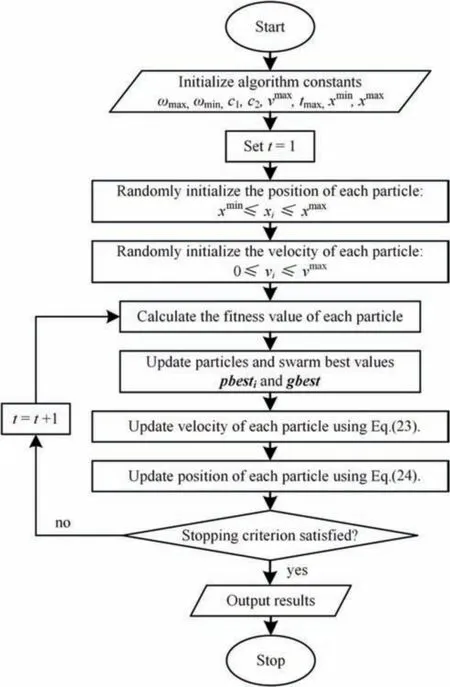
Fig.6.Optimization framework of PSO algorithm.

The propylene RS was optimized in this study by the cross-level model and the non-cross-level model separately,and we employed the same average heat capacity (Cp) as Dinhet al.[10] did to estimate the enthalpy changes.In each model,the independent variables were selected according to the degree of freedom,as shown in Table 1.Herein,the temperature at level 0 (T0) was pre-fixed to 40.9 °C,instead of being optimized.The temperature at level 4(T4)was determined by the minimum outlet temperature of hot process streams,with the minimum temperature approach in the HEN set as 2 °C.Both of the two models were solved by PSO algorithm.The structure of the optimal results is shown in Fig.9(a) and (b).

The optimal results of the propylene RS are summarized in Table 3.We have compared the total compressor shaft work (W)of the base case,the optimal result by Dinhet al.[10]and the optimal results by PSO in this study.In Dinhet al.[10],MILP model was established and solved by deterministic algorithm (BARON solver)based on a simplified model,which only considered parallel connection of sub-coolers and expansion valves,and discrete optimization of temperature levels.The result of isentropic compression from Dinhet al.[10]was transformed into polytropic compression in this case study,thus the specific shaft work was calculated by polytropic compression formula (Eq.(3)).As listed in Table 3,the optimizedWobtained by PSO (cross-level 6297 kW,non-cross-level model 6271 kW) are smaller than that obtained by deterministic algorithm in Dinhet al.[10](6403 kW).Compared with the cross-level model,theWsaving by the non-cross-level model is further increased (19.14%),with less CPU time (1.20 s) and greater success rate (80%).

5.4.Results and discussion

Analyzing the results in Case 1 (Table 2) and Case 2 (Table 3),discussions are summarized as follows:

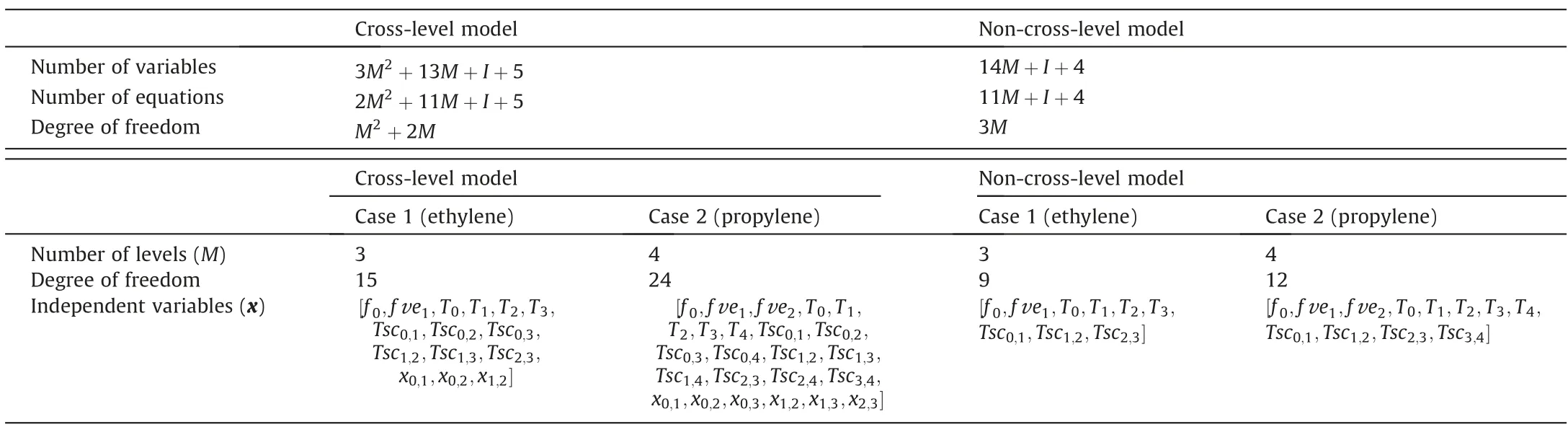
Table 1 Degree of freedom in the cross-level model and the non-cross-level model

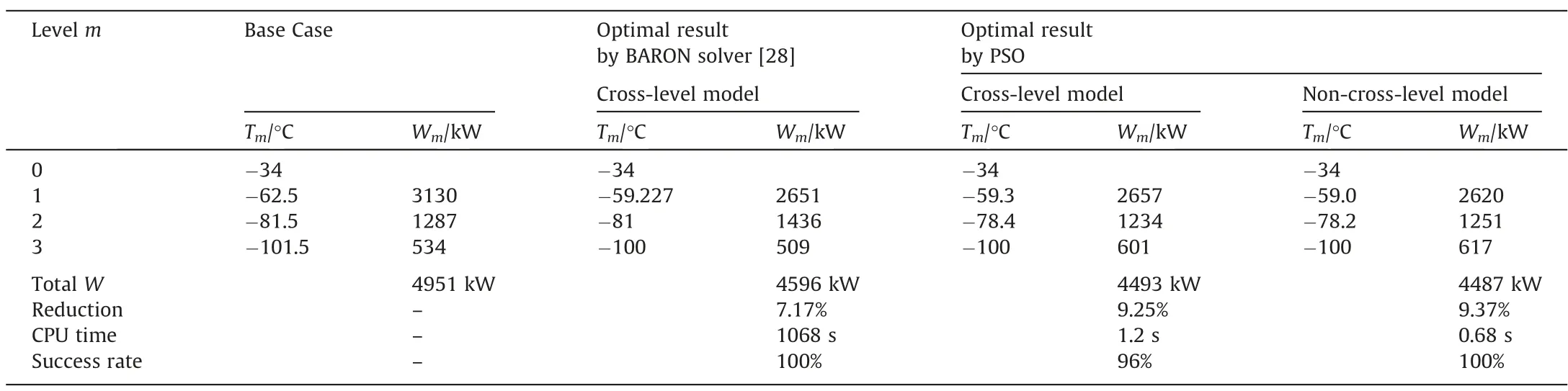
Table 2 Comparison between the base case and optimal results of the ethylene case study

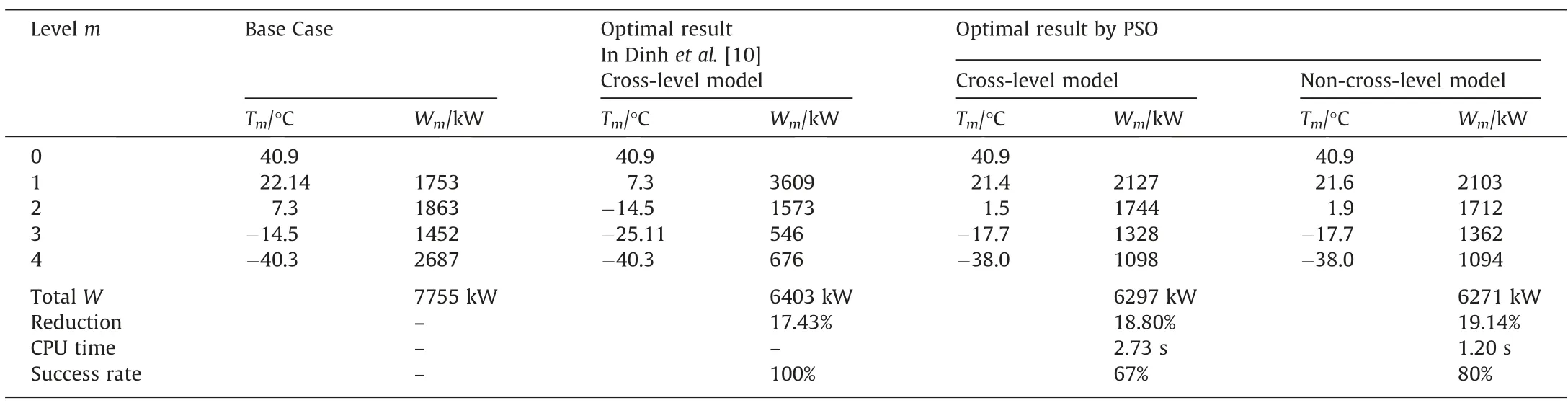
Table 3 Comparison between the base case and optimized results of the propylene case study

(i) The optimization study of the two example cases shows that the non-cross-level model (with redundancy removal) can get better results with less CPU time and greater success rate.Comparing the optimal results of the ethylene and the propylene RS,we can see that the advantage of the non-cross-level model is more obvious in the propylene case.Therefore,the more complex the problem is,the stronger the optimization effect will be brought by redundancy removal.

(ii) Comparing the results by deterministic algorithm and PSO in the two cases,we can see that PSO can effectively solve the comprehensive model and get better optimal results.Therefore,PSO algorithm is better at solving the large-scale nonconvex MINLP problem for the simultaneous optimization of the HEN and RS.

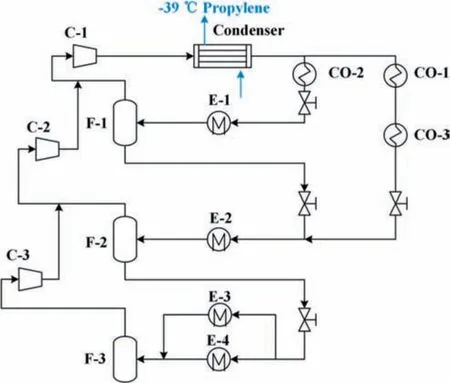
Fig.7.Structure diagram of the original ethylene RS.

(iii) Theoretically,the non-cross-level model is a special case of the cross-level model,the two kinds of models should get the same optimal results.The slightly different optimal results in case study are caused by the performance of the stochastic algorithm PSO.When using PSO to solve the complex large-scale non-convex MINLP model,it is possible to fall into locally optimal solutions.The more complex the model is,the more likely it is to fall into poor locally optimal solutions.Thus,the cross-level model (with larger dimension) is more likely to fall into locally optimal solutions.As for the non-cross-level model,after redundancy removal,the model complexity is greatly reduced(with less variables and equality constrains),thus reducing the solving difficulty and leading to a better result.

6.Conclusions

Synthesis of the RS is an essential contributor for reducing energy consumption.In this work,we have effectively solved the large-scale non-convex MINLP problem for the simultaneous optimization of a RS and its related HEN by developing a more comprehensive and compact model.We have revealed several insights as follows:

(1) The ‘‘two-step transformation method” is proved to be rational and effective for redundancy removal of the superstructure.

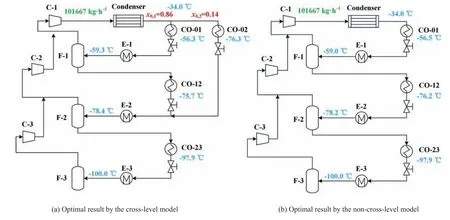
Fig.8.Structure diagram of the optimal ethylene RS by two models.

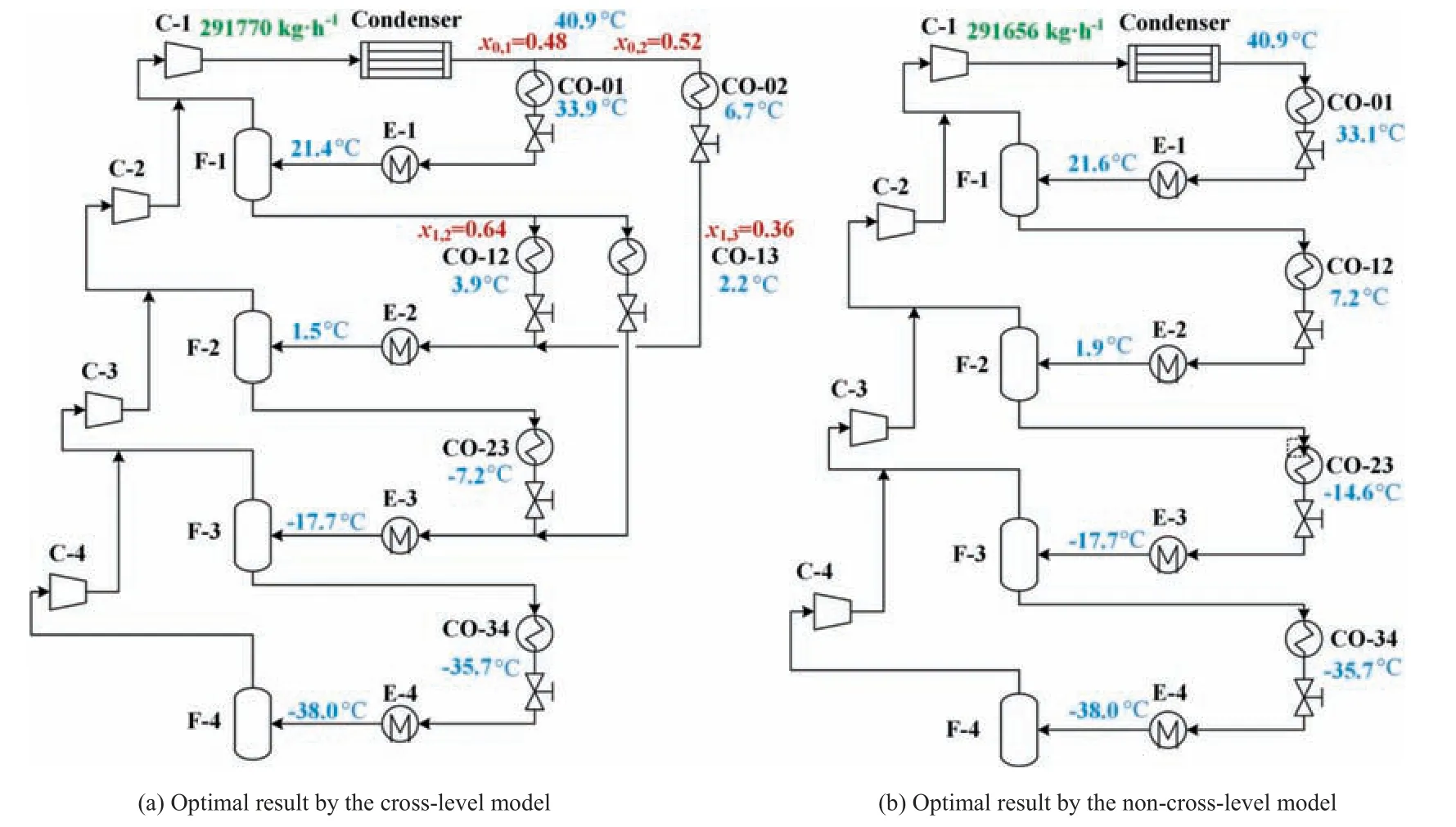
Fig.9.Structure diagram of the optimal propylene RS by two models.

(2) The established de-redundant model can greatly reduce the model scale and solving difficulty,with guaranteeing a relatively complete solution space.

(3) PSO algorithm can be used to solve this large-scale nonconvex MINLP problem.

(4) The methodology performs well in both of ethylene and propylene case studies with better optimal results and less CPU time.

In addition,this study offers insights on modelling redundant removal and stochastic algorithms application for future optimal synthesis of some relevant complex process systems.Due to the objective of minimizing total compressor shaft work in this study,we cannot optimize the number of pressure/temperature levels.In our future work,considering the optimization of the counts of pressure/temperature levels,we will realize the simultaneous optimization with the target of minimizing total annual cost(considering both energy consumption and capital cost).

Nomenclature

a1,a2,b,b1,b2fitting coefficients only related to refrigerant selection

Cpaverage heat capacity of the refrigerant,kJ·kg-1·℃-1

c1,c2acceleration constants in PSO

fsolution obtained by the PSO

fcmmass flow rate through the compressor from levelm,kg·h-1

femmass flow rate of the liquid discharge from the flash drum of levelm,kg·h-1

fgmmass flow rate of the vapor discharge from the flash drum of levelm,kg·h-1

fscm,m+1mass flow rate of sub-cooler from levelsmtom+1,in cross-level model,kg·h-1

fvemmass flow rate of vapor produced by the evaporator at levelm,kg·h-1

fvmmass flow rate of vapor produced by the expansion valve at levelm,kg·h-1

fvm,m+1mass flow rate of vapor produced by the expansion valve from levelsmtom+1,in cross-level model,kg·h-1

fxmmass flow rate through the sub-cooler at levelm,kg·h-1

f0mass flow rate through the condenser at level 0,kg·h-1

gbestjpast global best position of the swarm in PSO

HFm,m+1enthalpy of the inlet refrigerant at the expansion valve from levels m tom+1,kJ·kg-1

HLmenthalpy of the saturated liquid at levelm,kJ·kg-1

HVmenthalpy of the saturated vapor at levelm,kJ·kg-1

Δhrmgasification latent heat of the refrigerant at levelm,kJ·kg-1

Mrmolar mass of the refrigerant,g·mol-1

mTpolytropic index of compression of the refrigerant

Nallnumber of tests in PSO

Nsuccessnumber of successful tests in PSO

Pmpressure of levelm,kPa

pbestijpast best position of thei-th particle in PSO

QCiheat duty of cold process streams at intervaliin the HEN,GJ·h-1

QCi,cheat duty of thec-th cold process stream at intervaliin the HEN,GJ·h-1

QHiheat duty of hot process streams at intervaliin the HEN,GJ·h-1

QHi,hheat duty of theh-th hot process stream at intervaliin the HEN,GJ·h-1

Qti,mheat duty of the sub-cooler at levelm,within intervaliin the HEN,GJ·h-1

Qxmheat duty of the evaporator at levelm,GJ·h-1

Rmolar gas constant,which is 8.314 J·mol-1·K-1

Riresidual heat of intervaliin the HEN,GJ·h-1

SM={1,...,M} set of temperature levels

ST={1,...,I} set of temperature intervals in HEN

tnumber of iterations in PSO

Tmtemperature of levelm,℃

Tscmoutlet temperature of the sub-cooler at levelm,℃

Tscm,m+1outlet temperature of the sub-cooler from levelsmtom+1,in cross-level model,℃

UCiheat duty of cold utilities at intervaliin the HEN,GJ·h-1

UHiheat duty of hot utilities at intervaliin the HEN,GJ·h-1

vfmvapor fraction of the expansion valve at levelm

vfm,m+1vapor fraction at the expansion valve from levelsmtom+1,in cross-level model

vijvelocity of thei-th particle in thej-th dimension in PSO

winertia weight in PSO

Wtotal compressor shaft work,kW

wfmspecific shaft work of the compressor from levelm,kJ·kg-1

Wmshaft work of the compressor from levelm,kW

x set of independent variables

xii,mbinary variable,which equals 1 when them-th evaporator exists in intervali;otherwise,it equals 0

xijposition of thei-th particle in thej-th dimension in PSO

Zmaverage compressibility factor at levelm

γ1,γ2random numbers between 0 and 1,in PSO

ηmmechanical efficiency of compressor,which is 0.97

ηppolytropic efficiency of compressor,which is 0.72

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This research was supported by the National Natural Science Foundation of China (21978203) and the Natural Science Foundation of Tianjin (19JCYBJC20300).

Supplementary Material

Supplementary data to this article can be found online at https://doi.org/10.1016/j.cjche.2022.06.007.