Yubai Liu ,Zhiyuan Yu ,Thomas Pelster ,Ting-Tai Lee ,Yujun Wang, *,Guangsheng Luo

1 State Key Lab of Chemical Engineering,Department of Chemical Engineering,Tsinghua University,Beijing 100084,China

2 Evonik Operations GmbH,Brühler Stra?e 2,Wesseling 50389,Germany

3 Evonik Specialty Chemicals (Shanghai) Co.,Ltd.,Shanghai 201108,China

Keywords:Silica Nucleation Growth Mathematical modeling Mass transfer Surface reaction

ABSTRACT A mathematical model is developed for the calculation of the nucleation and growth process of silica nanostructured particles prepared by using the drop-by-drop method,and the calculation results of the proposed model is compared with the experimental value obtained from SAXS data.The model provides a non-ideal improvement in the supersaturation calculation and considers the impact of both mass transfer and surface reaction on the particle growth rate.The nucleation and growth rates are coupled depending on the change in monomer concentration over time,based on which the particle size and distribution are calculated.The growth curve of the silica particles from 3 nm to 20 nm and the change in particle number from 0 to over 1020 are calculated,which are consistent with the experimental values,establishing the reliability of the model.The calculations of the growth rate reveal that mass transfer controls the growth of silica particles before 10 min and the surface reaction is the rate-determining step after 10 min.The changes in the model parameters obtained by fitting with the SAXS data under different reaction conditions indicate the sensitivity of the corresponding process to different conditions.Moreover,the relationship between the particle growth rate and monomer concentration change is analyzed using the proposed model.

1.Introduction

Nanostructured silica is a high-performance powdered material that has wide applications in rubber,plastics,paint,medicine,adsorption separation,and heterogeneous catalysis [1-8].Various properties of silica are enhanced for specific applications.Hence,the process of producing silica nanostructured particles should be studied in detail.The precipitation process of silica by using sodium silicate and sulfuric acid is the most commonly used method for the production of nanostructured silica in the industry.Researchers have reported that silica nanostructured particles with various morphologies,pore structures,and surface properties can be obtained by adjusting the synthesis parameters during precipitation[9-12].However,the in-depth study,especially model study for the nucleation and growth mechanism behind the particle formation process is still insufficient.

The key to establishing a reliable nucleation and growth model is to obtain sufficient data of the particle formation from experiments.Consequently,many classical mechanisms related to the particle formation still have limitations in terms of the fitness with experimental data and the predictive ability,such as the classical nucleation theory [13,14],LaMer theory [15],Ostwald ripening mechanism [16],and four-step autocatalysis model [17],although they provide a certain description and explanation of the nucleation and growth of nanoparticles based on thermodynamics or reaction processes.The development of various characterization techniques and experimental equipment provides powerful solutions to performin situandex situmeasurements of nanoparticles.Small angle X-ray scattering(SAXS),dynamic light scattering(DLS),andin situtransmission electron microscopy(TEM)have facilitated the probing of particles in solutions to obtain their growth information instantaneously.This provides detailed information regarding the nucleation and growth processes of nanoparticles,resulting in advanced growth models [18,19].The calculations obtained from these models are more consistent with the experimental data,leading to a deeper understanding of the formation mechanism of nanoparticles.Based on that,the formation of silica nanostructured particles is also investigated by researchers [20-23].These studies provide great knowledge regarding the particle formation mechanism,and some models even provide good predictions.However,few studies have been conducted on the formation of precipitated silica nanostructured particles.Moreover,most of the aforementioned models can only provide the results of the final particle size under different synthesis conditions (such as concentration),but not show the change in particle size over time or provide information on the nucleation rate or the growth rate.Therefore,a systematized model-based study of silica precipitation is necessary.

It is worth noting that silica precipitate is unique compared with other common precipitation systems.The precipitation reactions in solutions are usually ionic reactions,such as those of barium sulfate and calcium carbonate.This type of reaction occurs owing to direct collisions between ions that do not need to cross a high-energy barrier,leading to a fast reaction rate.Therefore,the growth of such precipitated particles is mostly controlled by diffusion.However,the growth of silica particles depends on the condensation reaction between Si-OH groups on the surface of the particles,and the condensation reaction contains a series of intermediates and transition states.The energy barrier of the condensation reaction is higher than that of the ionic reaction.Therefore,this reaction is slower than the ionic reaction under the same conditions.In fact,precipitation reactions(for example,the precipitation reaction of barium sulfate)can occur at room temperature,whereas the precipitation reaction of silica in industry usually requires heating.Therefore,in a slow reaction process of silica,it should be considered whether the growth process will be controlled by the reaction,not just by the diffusion.Hence,a unique model explaining the growth of silica nanostructured particles is necessary.Our research group[24]used SAXS to follow the precipitation process of silica nanostructured particles with drop-bydrop method,and obtained the change in both particle size and relative particle number,which showed a three-stage growth mode of silica particles.Moreover,it was found that the second stage was controlled by the surface reaction of Si-OH group.Based on this research,a mathematical model for the calculation of nucleation and growth of precipitated silica particles can be developed to explore the mechanism of silica formation and verify the conclusions obtained from the SAXS experiments.

In this study,a mathematical model is proposed to explain the nucleation and growth processes of precipitated silica nanostructured particles,and the calculation results were compared with SAXS experimental data.In the calculation of the growth part,the impact of the mass transfer and surface reaction on the particle growth rate were both considered.The nucleation and growth rates were coupled through mass conservation,based on which the particle size and number over time were calculated.The model calculation results were found to be consistent with the experimental data.The estimated values of the adjustable parameters under different reaction conditions indicated the existence of different growth mechanisms.The proposed model exhibited good predictive ability and stability and provided an in-depth understanding of the formation mechanism of precipitated silica.

2.Model Description

2.1.Model structure

The proposed nucleation and growth model of silica nanostructured particles was established based on the drop-by-drop method described in detail in a previous study,in which 10%(mass)sulfuric acid is added as a constant dripping rate into 78 g 21.4%(mass)sodium silicate solution (which has been diluted with 200 ml water before acid dripping)[24].This is a simplified industrial production method that retains its reaction characteristics.Moreover,it facilitates an analysis of the condensation reaction by controlling the addition of H+.

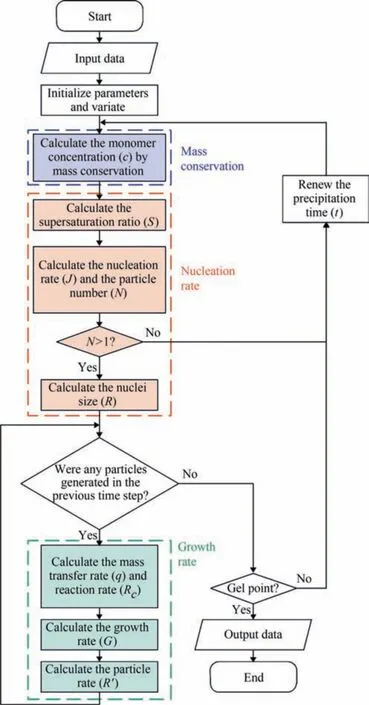
Fig.1.Flow chart of the mathematical model for the nucleation and growth of silica nanoparticles by using the drop-by-drop method.

A logical structural diagram of the model is shown in Fig.1.The formation process of silica nanostructured particles can be divided into two parts: nucleation and growth.Considering that both the nucleation and growth processes consume monomers,and the monomer concentration in a solution has an effect on the rates of these two processes.Hence,the calculation of the nucleation and growth rates is coupled by the mass conservation of the monomer.In this way,the three main parts of the model are represented by different colors in Fig.1.The basic physical parameters(such as the solubility of silica,diffusion coefficient of the monomer,and specific surface energy of the cluster/solution interface)and initial reaction conditions (such as the reaction temperature,initial volume of the solution,concentration,and dripping rate of the raw material) are defined.Subsequently,the variables that change based on the change in the reaction time,such as the nucleation rate,growth rate,particle size,and particle number,are initialized to 0.Moreover,parameters,such as the time step and total reaction time,are initialized as well.It is worth mentioning that the particle size will not only vary over time,but also be distinct among silica particles generated at different times.The monomer concentration in the solution is calculated based on material balance.Subsequently,the nucleation and growth rates can be obtained based on the monomer concentration,so the size of silica particles after nucleation and growth can be calculated.There are two details to be noted here.First,it is necessary to judge whether there is nucleation according to the particle number.Nucleation does not occur when the number of particles is extremely small.Hence,the monomer will be added to the solution to increase the supersaturation ratio.Besides,there are silica particles with different residence time in the solution,so their size must be calculated separately in each calculation cycle.Calculations are terminated when the calculation time reaches the gel point under reaction conditions.This is because the viscosity of the system increases considerably after the gel point,which changes the properties of the solution substantially and alters both the diffusion and reaction rates of the monomer,making the proposed model unsuitable for calculations.The specific calculation method for this model is described in the following sections.

2.2.Nucleation rate

Tobleret al.[22] demonstrated that the nucleation of precipitated silica nanostructured particles can be considered as an instantaneous process.Many researchers have proposed classic formulas for calculating the homogeneous nucleation rate based on the work done in particle nucleation and collision nucleation mechanisms,in which the frequencies of monomer attachment and detachment,including the monomer diffusion and reaction,have already been considered [25].

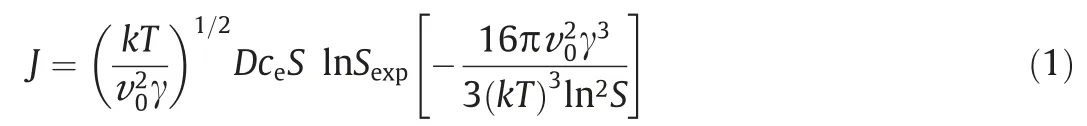
In this equation,J(m-3·s-1)is the nucleation rate,kis the Boltzmann constant,T(K) is the temperature,v0(m3) is the molecular volume of the monomer,which can be calculated from v0=M/(ρNA) [whereM(g·mol-1) is the molecular weight,ρ(g·m-3) is the density,NAis Avogadro’s number],γ(J·m-2)is the specific surface energy,D(m2·s-1)is the monomer diffusion coefficient,andce(m-3) is the solubility that can be calculated by applying the following equation [26]:

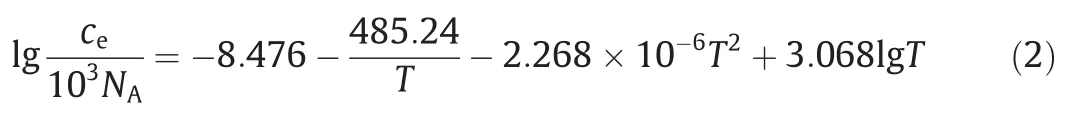
The key parameter in Eq.(1) is the supersaturation ratioSthat can be calculated by using the following equation:

wherec(m-3) is the molecular concentration.Moreover,a(m-3)andae(m-3) are the actual and equilibrium activities of the monomer in a solution,respectively.In the precipitation process,the nonideality of the solution must be considered when the monomer concentration in the solution becomes high.Therefore,the activity coefficient (γ±) is introduced to account for the non-ideality of the solution.The supersaturation ratio,S,appears three times in Eq.(1),representing increasing functions: therefore,the cumulative impact of the increase inSleads to a significant increase in the nucleation rate.The number of monomers in the formed nuclei is calculated by using the following equation:

Therefore,the number of monomers contained in the nuclei is small when the supersaturation ratio is large,and the size of the nuclei is small accordingly.The nuclei size is the same as the initial size of silica particles,obtained by applying the following equation:

Moreover,the number of particles can be obtained based on the nucleation rate as follows:

wheret(s) is the time.

2.3.Growth rate

The formation of silica nanostructured particles depends on the dehydration condensation reaction between the surface Si-OH groups.Hence,the growth is a series of processes,including mass transfer and surface reaction,as shown in Fig.2.The monomer molecules first diffuse to the surface of the particles and conduct the surface reaction.Therefore,the slower of the two processes is the rate-limiting step of the entire growth process.The calculation for the two processes was performed separately.

The drop-by-drop method was performed under mechanical stirring.The stirring Reynolds number (Re) of the process was calculated as follows:

whereDst(m) is the diameter of the stirring paddle,n(s-1) is the rotating speed,ρsol(kg·m-3) is the density of the solution,and μ(Pa·s)is the viscosity.The calculations demonstrated turbulent flow in the beaker.Hence,the actual mass transfer process was not only molecular diffusion.The stirring effect greatly enhanced the mass transfer,so the mass transfer resistance of the bulk phase can be ignored.All of the mass transfer resistance can be considered to be concentrated in the diffusion zone (δ) near the particles in a micron to sub-millimeter size range.The mass transfer process can be simplified to a diffusion mass transfer in a spherical coordinate system as shown in Fig.3.Therefore,the mass-transfer flux can be calculated as follows.

The boundary conditions are as follows:

whereNA(mol·m-2·s-1) is the mass transfer flux andJA(mol·m-2-·s-1) is the diffusion flux.Therefore,the mass transfer rate of the particle surface can be calculated by using Eq.(13):

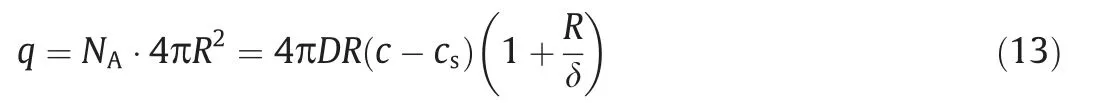
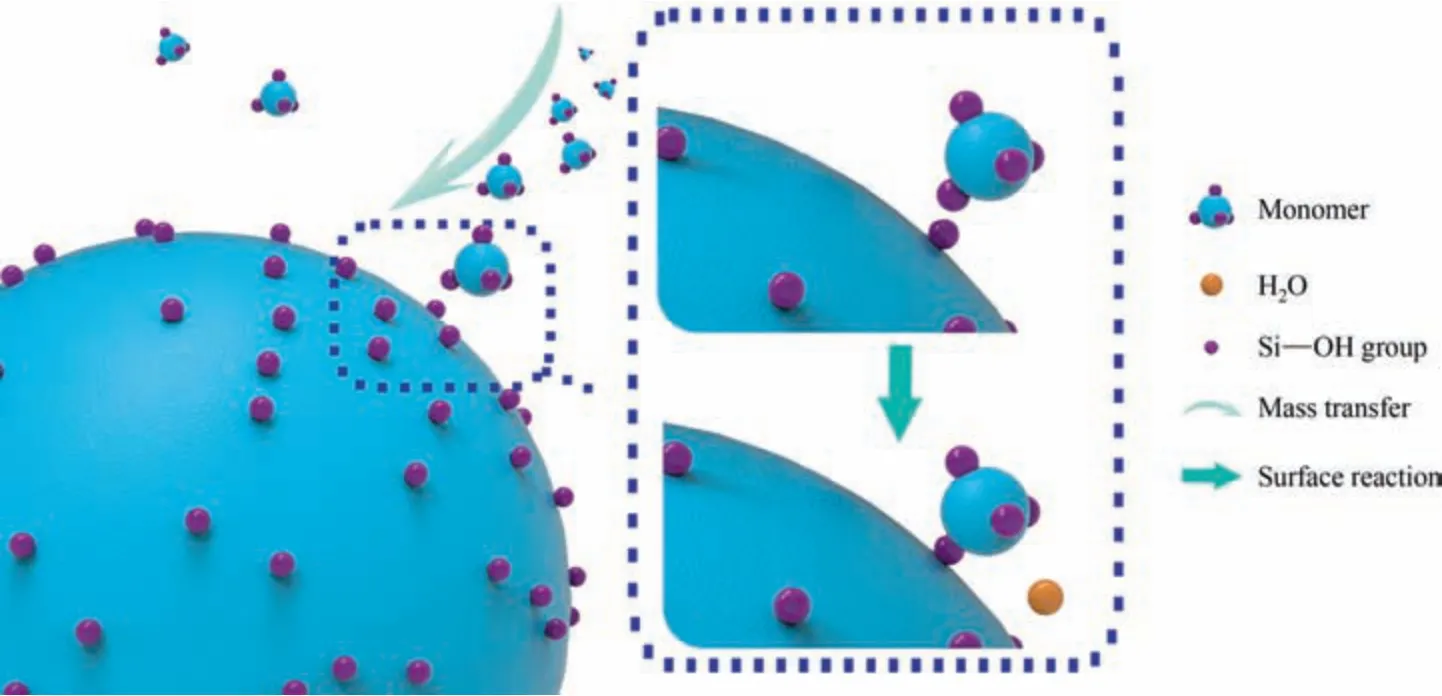
Fig.2.Schematic diagram of the tandem relationship between mass transfer and surface reaction during the growth of silica nanostructured particles.

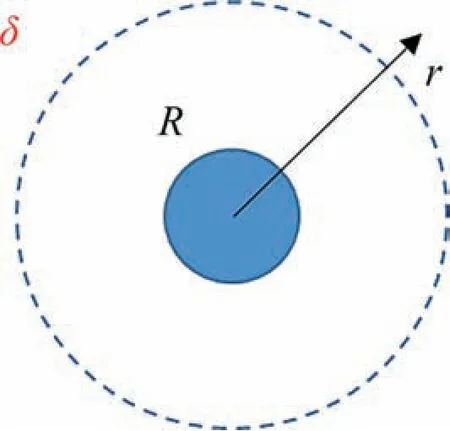
Fig.3.Schematic diagram of mass transfer rate calculation during the growth of silica nanostructured particles.

The silica particles are usually in the nanometer scale.Hence,δ is significantly larger thanR.Eq.(13) can be approximated as:

wherecs(m-3) is the monomer concentration at the surface of the silica nanostructured particles,calculated by using the Gibbs-Thomson equation [27,28] as follows:

Moreover,the effects of the temperature,viscosity,and electric double layer on the diffusion coefficient cannot be determined directly.Hence,a correction of the diffusion coefficient is introduced as follows:

The mass transfer rate can be obtained by using the initial particle size and monomer concentration.The particle size and monomer concentration in the bulk phase were small in the initial stage resulting in a large surface monomer concentration.Thus,the driving force behind mass transfer was small,and the mass transfer rate was slow.The monomer concentration increased when sulfuric acid was added to the solution.Meanwhile,the particle size increased with growth leading to a decrease in the surface monomer concentration.Thus,the driving force behind mass transfer increased and the mass transfer rate increased as well.However,the increase in the mass transfer rate slowed when the monomer concentration reached its peak and subsequently decreased.

The reaction path of the condensation of Si-OH was calculated using DFT,and the maximum free energy barrier of 73.9 kJ·mol-1was obtained for the condensation process under alkaline conditions in a past study[24].The reaction rate constant of the condensation reaction can be calculated based on this information.Thus,the rate of the surface condensation reaction can be directly calculated as follows:

For the actual particle growth process,it is also necessary to consider the change of the reaction site with the particle growth.The power law correction is usually applied as follows [29]:

whereLis a length value for dimensionless processing.It is set to 20 nm in the proposed model,which is in the same order of magnitude as the size of the silica nanostructured particles.According to Eq.(18),the reaction rate is not related to the particle size when exponentais zero.Moreover,it can be indicated that all monomers(or a fixed ratio of monomers) in the particle are potential reaction sites when the exponentais three.For the particle growth process,the surface reaction rate is proportional to the possible bonding sites on the particle surface.Therefore,awill be two for smooth particles and surface roughness will push it close to three.

After calculating the mass transfer rate and the reaction rate,the impact of the two on the particle growth rate needs to be considered.If the driving forces of the mass transfer and the surface reaction are respectively assumed to beAandB,the particle growth rate can be calculated from the following equation:

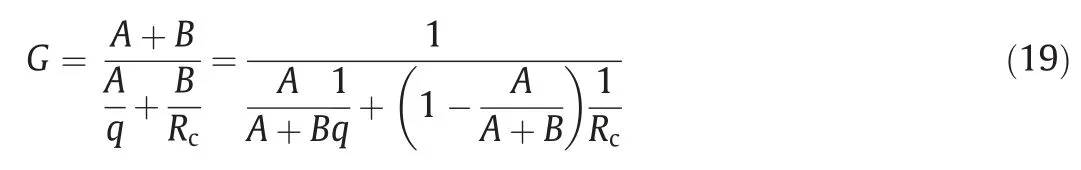
Ifzis demanded to be equal toA/(A+B),which represents the magnitude of the mass transfer driving force relative to the total driving force,Eq.(19) can be simplified as follows:

Subsequently,the particle size after growth can be calculated by using the following equation:

whereV(m3) is the volume of the solution.

2.4.Mass conservation

Monomer is consumed in both the nucleation and growth processes,and the addition of sulfuric acid provides new monomers.Hence,the mass conservation of monomers can be calculated after obtaining the nucleation and growth rates.The rate of change in the monomer concentration is equal to the rate of monomer generation minus the rate of monomer consumption:

The monomer generation rateNpro(m-3·s-1)is equivalent to the H+dripping rate owing to the excessive amount of sodium silicate.The addition of H+shifts the hydrolysis equilibrium to the right,which in turn changes the monomer generation rate and monomer concentration,indicating that the equilibrium state of the hydrolysis reaction affects the kinetic rate of the condensation reaction through the monomer concentration.The consumption rate of nucleation to the monomer is.

and the consumption rate of growth to monomer is given as follows:

So far,the establishment of the model has been completed.The monomer concentration in the solution after particle nucleation and growth is calculated based on the input of the temperature,concentration,and dripping rate using iterative time steps.Subsequently,the change in the particle size,particle number,nucleation rate,growth rate,and other information over time can be outputted.

3.Results and Discussion

3.1.Model validation

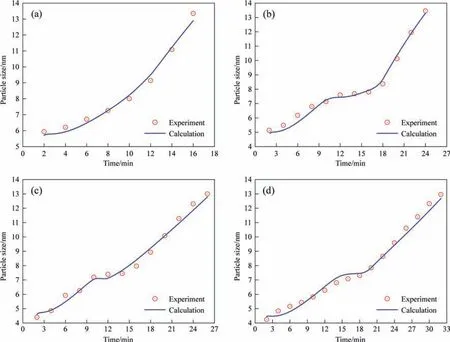
Fig.4.Comparison of calculated growth curve of silica nanostructured particles with experimental data at reaction temperatures of (a) 363 K,(b) 353 K,(c) 343 K and (d)333 K,respectively (Sulfuric acid dripping rate: 1.2 ml·min-1).

The three-stage growth of silica nanostructured particles during the drop-by-drop precipitation process was monitored using SAXS in a past study.Therefore,the operating parameters of the dropby-drop method were applied as input data to validate the proposed silica nucleation and growth model.The calculations obtained from the proposed model were compared with the experimental values obtained from SAXS analysis in the past study to validate the rationality of the proposed model.The experimental results showed that the particle size primarily changed in the first two stages,and the third stage involved the formation of a pore structure.Moreover,the viscosity of the entire system increased significantly in the third stage resulting in significant changes in physical properties,such as the diffusion coefficient,making it unviable for the proposed model analysis.Therefore,our model calculation included only the precipitation process of the first two stages before the gel point in the experiment.The physical properties of the silica precipitation system used in the proposed model are listed in Table 1.The simulation results of the change in silica particle size with time under different reaction temperatures and sulfuric acid dripping rates (same as the experimental conditions)was compared with the experimental data,as shown in Figs.4 and 5,respectively.The calculated values for various reaction conditions are in good agreement with the experiment results.The rate of change in the growth curves of the silica nanostructured particles at different reaction temperatures obtained using the proposed mathematical model can correspond to the monomer accumulation stage and the growth stage obtained in the experiments,as shown in Fig.4.The calculated growth curves in Fig.5 demonstrate that the monomer accumulation stage gradually disappears corresponding to an increase in the sulfuric acid dripping rate.This observation is consistent with the conclusion established in a past study.Moreover,the change in the particle size distribution over time was obtained from calculations as shown in Fig.6.The change in particle size distribution was consistent with the observations in the experiment.In the first stage,small particles with sizes less than 10 nm were generated.During the growth stage,the nucleation rate gradually decreased,resulting in a decrease in the number of newly generated small particles.Meanwhile,the particle size increased significantly,and the particle size distribution gradually became more narrow.In addition,the calculation results of the particle number were also compared with the relative particle number obtained in the experiment.Although there is a little difference in the time of the nucleation,their change trends have a good consistency,as shown in Fig.7.Thus,the proposed nucleation-growth model is reliable to be used for further research on the correlation between the nucleation rate,mass transfer rate and surface reaction rate,and the effects of the fitting parameters.

Table 1 Values of the parameters of physical properties used for the calculation of the nucleation and growth of silica nanostructured particles in aqueous solutions

3.2.Rate-determining step

The growth of silica nanostructured particles depends on the slower condensation reaction on the particle surface (compared to the fast ionic reaction).Therefore,analyzing whether the ratedetermining step in the growth of silica particles is diffusion or reaction is necessary.In the previous study,the Liftshitz-Slyozov-Wagner (LSW) model was used to fit the experimental data of the particle size change with time in the growth stage,the result of which suggested a surface reaction control mechanism in the 333-363 K range.The calculations in this research validate this conclusion.According to Eqs.(16)and(18),silica particles of different sizes have different growth rates.Therefore,the mass transfer rate and the reaction rate were averaged based on the particles size distribution.Fig.8 illustrates the time-dependent changes in both the mass transfer rate and the surface reaction rate over the calculated range (that is,the monomer accumulation stage and the growth stage in the experiment).It can be seen that the mass transfer process and the surface reaction process alternately controlled the particle growth.In the first 10 min of the precipitation process,which corresponds to the monomer accumulation stage in the experiment,the mass transfer rate of the monomer is significantly slower than the surface reaction rate,so the growth of silica particles is controlled by mass transfer at this time.During 10-11 min,the mass transfer rate is close to the reaction rate.Therefore,it is a transitional state then with no obvious ratedetermining step.After 10 min,which corresponds to the growth stage in the experiment,the increase in the surface reaction rate is not as large as that in the mass transfer rate.Thus,the slower surface reaction rate limits the growth of silica particles,suggesting that the particles in the solution are mainly controlled by the surface reaction at this time.

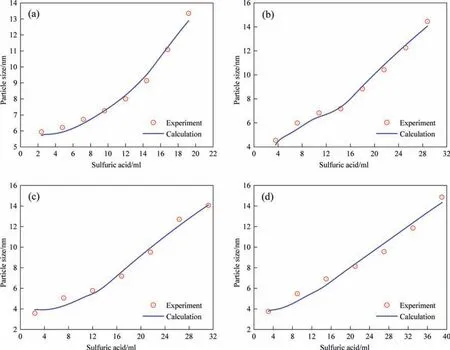
Fig.5.Comparison of calculated growth curve of silica nanostructured particles with experimental data with different sulfuric acid dripping rates of (a) 1.2,(b) 1.8,(c) 2.4,and (d) 3.0 ml·min-1,respectively.(Reaction temperature: 363 K).

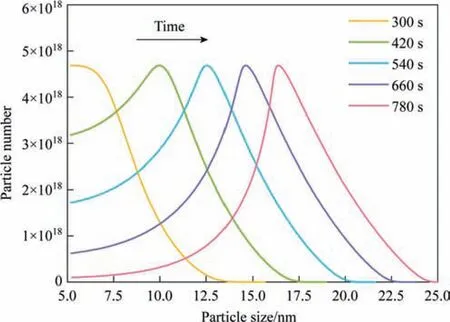
Fig.6.Calculated time evolution of the particle size distribution of silica nanostructured particles.(Reaction temperature: 363 K,Sulfuric acid dripping rate:3.0 ml·min-1).

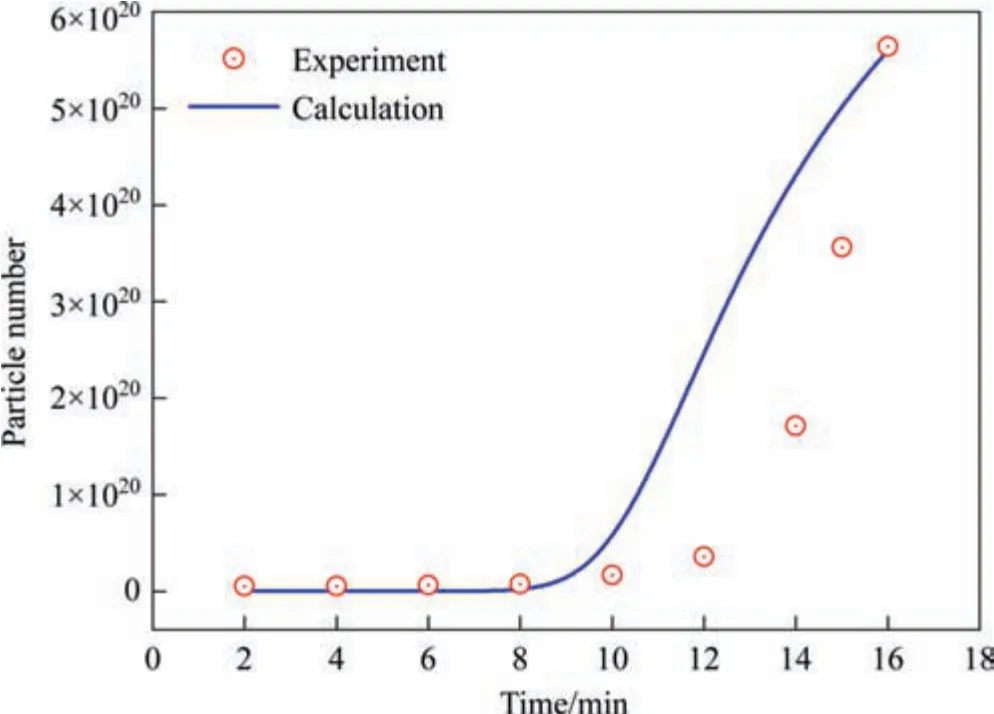
Fig.7.Change in the number of silica particles during the precipitation process.(Reaction temperature: 363 K,Sulfuric acid dripping rate: 1.2 ml·min-1).

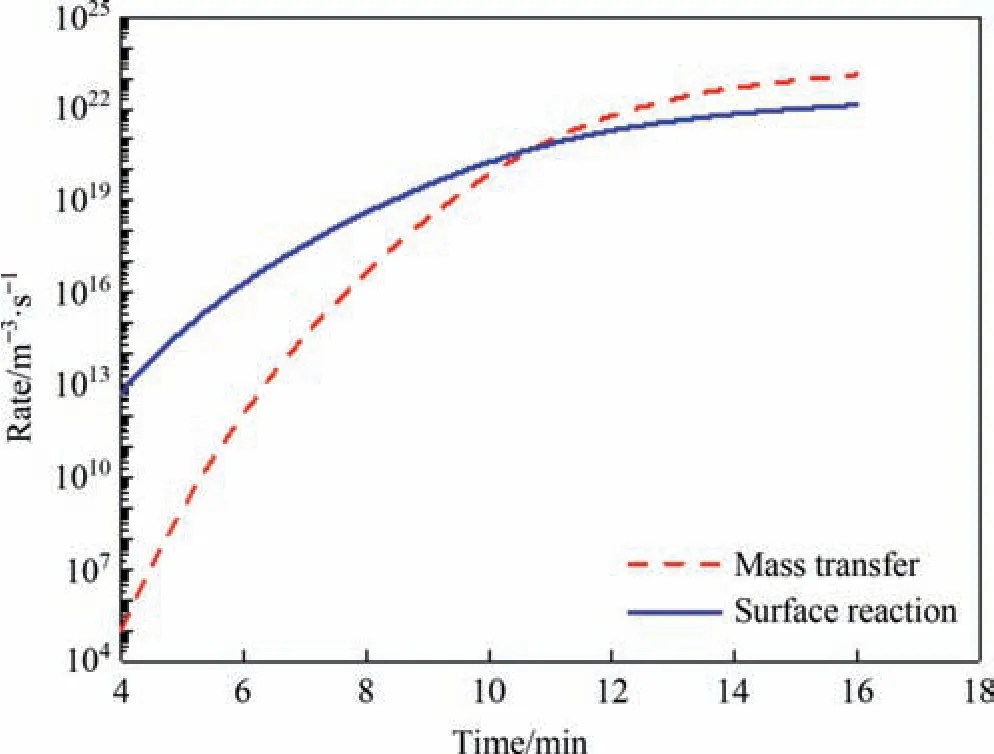
Fig.8.Changes in the mass transfer and surface reaction rates corresponding to time during silica particle growth.(Reaction temperature: 363 K,Sulfuric acid dripping rate: 1.2 ml·min-1).

The reason for the above phenomenon can be analyzed by calculation process.Particle size has an impact on both the mass transfer rate and the surface reaction rate based on Eqs.(15),(16),and(18).However,the silica nanostructured particles formed at different times had different initial sizes because of the constant change in supersaturation in the solution based on Eq.(5).Meanwhile,the relative rates of mass transfer and surface reaction are also dependent on monomer concentration.In the monomer accumulation stage,the low concentration of monomer led to a small mass transfer driving force and slow mass transfer rate.Hence,the particle growth was controlled by diffusion.As the driving force of the mass transfer increased with the accumulation of monomers in the solution,the mass transfer rate increased as well.This resulted in an increase in particle size and a decrease in the surface monomer concentration.This was detrimental to the increase in the surface reaction rate.Therefore,the surface reaction was the rate-determining step.However,the rapid growth of silica particles consumed large quantities of monomer.Moreover,the limited waterglass prevented the continuous generation of the monomer.The monomer concentration in the solution began to decline when the consumption rate of the monomer was greater than the supply rate,which had a significant impact on the mass transfer rate.Therefore,it is possible that the mass transfer rate is smaller than the reaction rate again.

The growth rate of silica nanostructured particles was calculated based on diffusion control exclusively as shown in Fig.9 to demonstrate the impact of surface reaction on the entire growth process.It can be seen that the particle size calculated without considering surface reaction is larger than the experimental value for the particle size especially in the second stage,which further supports the analysis above.Moreover,a mean-field theory was used to fit the experimental data as denoted by the green line in Fig.9.However,this model cannot fit the data of both stages simultaneously because the different control factors of the two stages cannot be calculated using the same equation.This indicates the need for considering the change in the rate-determining step in the proposed model.

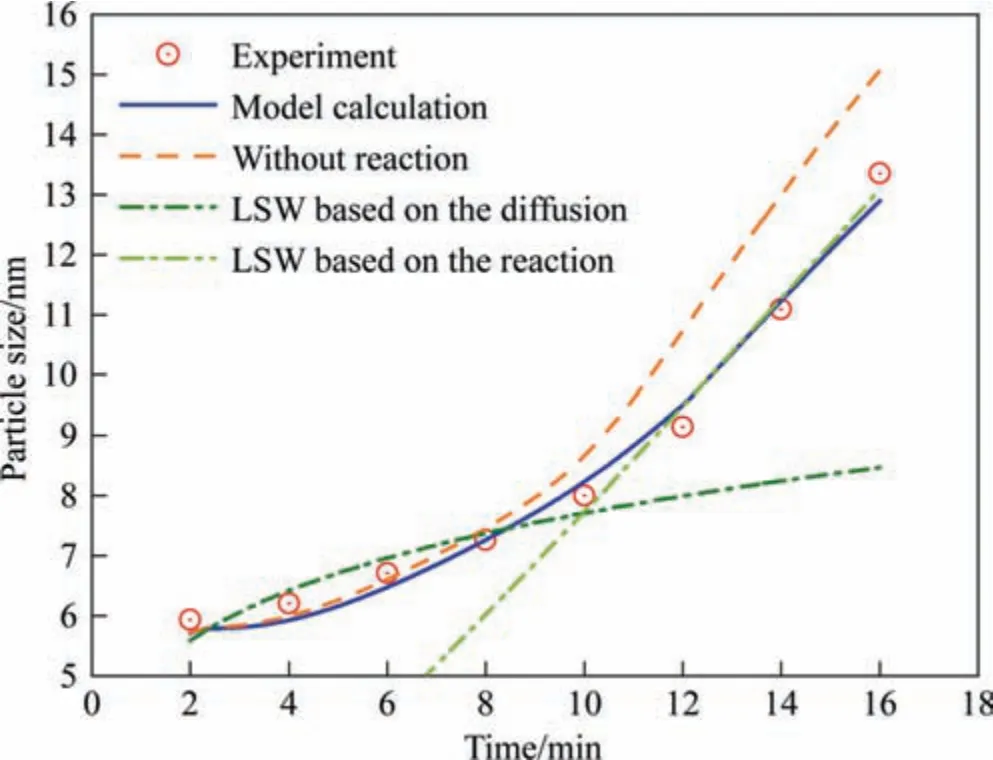
Fig.9.Comparison of calculated and experimental values for the growth process of silica particles through different models.(Reaction temperature: 363 K,Sulfuric acid dripping rate: 1.2 ml·min-1).

3.3.Fitting parameters

Three parameters cannot be directly obtained in the model as shown in Eqs.(3),(16),and (18).Therefore,the experimental data were fitted to obtain these parameters.It must be noted that every fitting parameter has its own physical meaning and is not used just to improve the fit of the experimental data.These parameters are helpful in understanding the entire process.The first parameter is the activity coefficient (as shown in Eq.(3)),representing the degree of deviation of the solution from the ideal state.This parameter depends on the temperature and ionic strength of the solution.The second parameter is the diffusion coefficient (as shown in Eq.(16)) whose exact value cannot be obtained.Hence,a correction based on temperature,monomer concentration,and the electric double layer near the particles is introduced.The third parameter is the exponentain the power correction (as shown in Eq.(18))used for calculating reaction rate to measure surface roughness.Moreover,the impact of different reaction conditions on the fitting parameters was analyzed.

The effect of temperature on fitting parameters was first investigated.The fitting results for the three parameters at different temperatures are listed in Table 2.Temperature is seen to have a significant effect on activity and diffusion coefficients.The intermolecular forces in the solution change corresponding to the changes in temperature,resulting in a change in the non-ideality of the solution.The fitting results in Table 2 reveal that the solution deviated more from the ideal state when the reaction temperature decreased.Moreover,the rate of molecular motion increases corresponding to increasing temperature leading to an increase in the diffusion coefficient.The fitting parameters obtained at 363 K,353 K,and 333 K were used to interpolate the fitting parameters at 343 K to test the reliability of the model.The outcome of this test is listed in Table 2.The interpolation parameters were used to per-form model calculations and the results are shown in Fig.10.The parameters values obtained by interpolation are almost the same as those obtained by fitting,and the results of model calculations using these interpolated parameters are also in good agreement with the experimental values.

Table 2 Values of parameters obtained by fitting and interpolating at reaction temperatures of 363 K,353 K,343 K,and 333 K,respectively.(Sulfuric acid dripping rate:1.2 ml·min-1)

The impact of acid dripping rate on the fitting parameters was analyzed in a similar manner.The fitting and extrapolation results of the three parameters with different acid dripping rates are listed in Table 3.Increasing the H+dripping rate alters the diffusion process significantly.The diffusion coefficient increased corresponding to an increase in the acid dripping rate.This is because the monomers in the solution can be generated rapidly by increasing acid dripping rate whereas an increase in H+dripping rate also changes the charge distribution in the solution leading to changes in the diffusion coefficient.Tables 2 and 3 reveal that the changes in the reaction temperature or acid dripping rate has no significant effect on the surface roughness of the particles.Similarly,extrapolation parameters were used for model calculations shown in Fig.11.The parameters obtained by extrapolation deviate from the fitting results.However,the calculated values are approximately equal to the values from experimental data,which demonstrates the reliability and predictive ability of the proposed model.

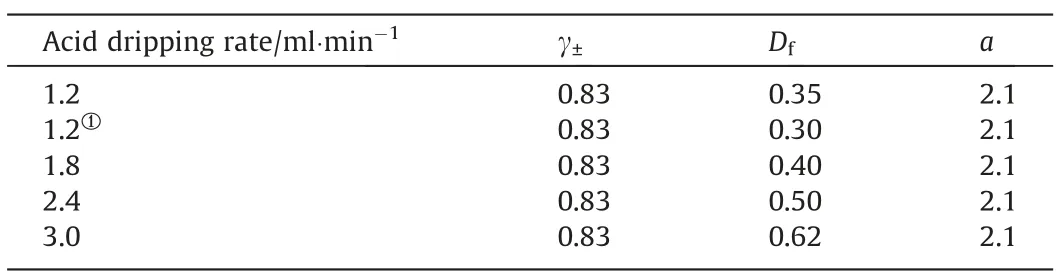
Table 3 Values of parameters obtained by fitting and extrapolating with the sulfuric acid dripping rates of 1.2,1.8,2.4,and 3.0 ml·min-1,respectively.(Reaction temperature:363 K)

The above analysis and discussion demonstrate the reliability of the proposed model,so a more in-depth analysis of the growth path based on the fitting parameters was conducted.The particle growth rate was varied by adjusting the fitting parameters to obtain different particle growth curves,as shown in Fig.12(a).The growth curve of the silica particles was based on the change in the monomer concentration.Therefore,the corresponding change in the monomer concentration with time is shown in Fig.12(b).It is obvious that monomer consumption increases corresponding to an increase in the particle growth rate.As analyzed in the previous section,the monomer concentration gradually increases with the addition of sulfuric acid,resulting in the increased nucleation rate.Meanwhile,the growth rate also increases due to the growing particles.These two factors together lead to increased consumption of monomers,while the rate of monomer generation remains unchanged.Therefore,when the consumption rate of the monomer is greater than the generation rate,the monomer concentration will decrease,resulting in a concentration peak,as shown by the blue line in Fig.12.It demonstrates that a change in monomer concentration changes the growth rate trend,and the growth rate also determines the monomer consumption rate.Thus,the growth rate and the monomer concentration exhibit a particular correlation.For the case of the purple curve,the monomer concentration continues to rise without a peak,indicating that the monomer consumption rate is less than the generation rate.This is because the solution deviates more from the ideal state when the monomer concentration is high,and the change of supersaturation is reduced,resulting in a stable nucleation rate.Thus,the consumption of monomer decreased.Therefore,the non-ideality of the solution is a key factor linking the monomer concentration to the nucleation and growth rate.If the monomer concentration has a flat peak,a corresponding flat growth phase can also be observed in the particle growth curve,as shown by the pink curve in Fig.12.This is due to changes in the driving force of mass transfer and reaction.In the initial stage,the driving force of mass transfer is relatively small,so the growth process is controlled by mass transfer.As the monomer consumption rate increases close to the monomer generation rate,a flat peak appears in the monomer concentration.However,the particles are still growing slowly,so the driving force for mass transfer increases according to Eq.(15),and the growth process enters a transitional state.Subsequently,the mass transfer driving force continues to increase,the reaction process becomes the ratedetermining step.At this time,the second inflection point appears in the particle growth curve.Therefore,the particle growth rate increases,and the monomer concentration begins to decrease.

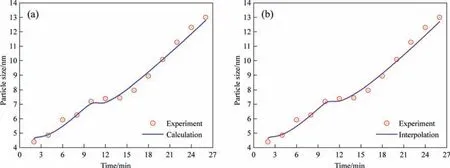
Fig.10.Comparison of calculated growth curve of silica nanostructured particles with experimental data at 343 K using (a) fitting parameters and (b) interpolation parameters.(Sulfuric acid dripping rate: 1.2 ml·min-1).

4.Conclusions

This work presented a mathematical model for the calculation of the nucleation and growth processes,including both mass transfer and surface reactions,of silica nanostructured particles prepared by using the drop-by-drop method.The proposed model showed a non-ideal improvement in the calculation of supersaturation in the existing nucleation-rate calculation method.The growth process of silica nanostructured particles was regarded as a series of monomer diffusion and surface reaction processes.The surface condensation reaction between Si-OH was slower than the general precipitation ion reaction.Hence,both diffusion and reaction may become the rate-determining step of the growth process.The mass transfer resistance was concentrated near the particles during the mass transfer process.The reaction rate constant was obtained from DFT calculations.Moreover,a power law correction was derived for the surface reaction sites.Furthermore,the nucleation and growth rates were coupled by the change in the monomer concentration over time based on the mass conservation of the monomer.

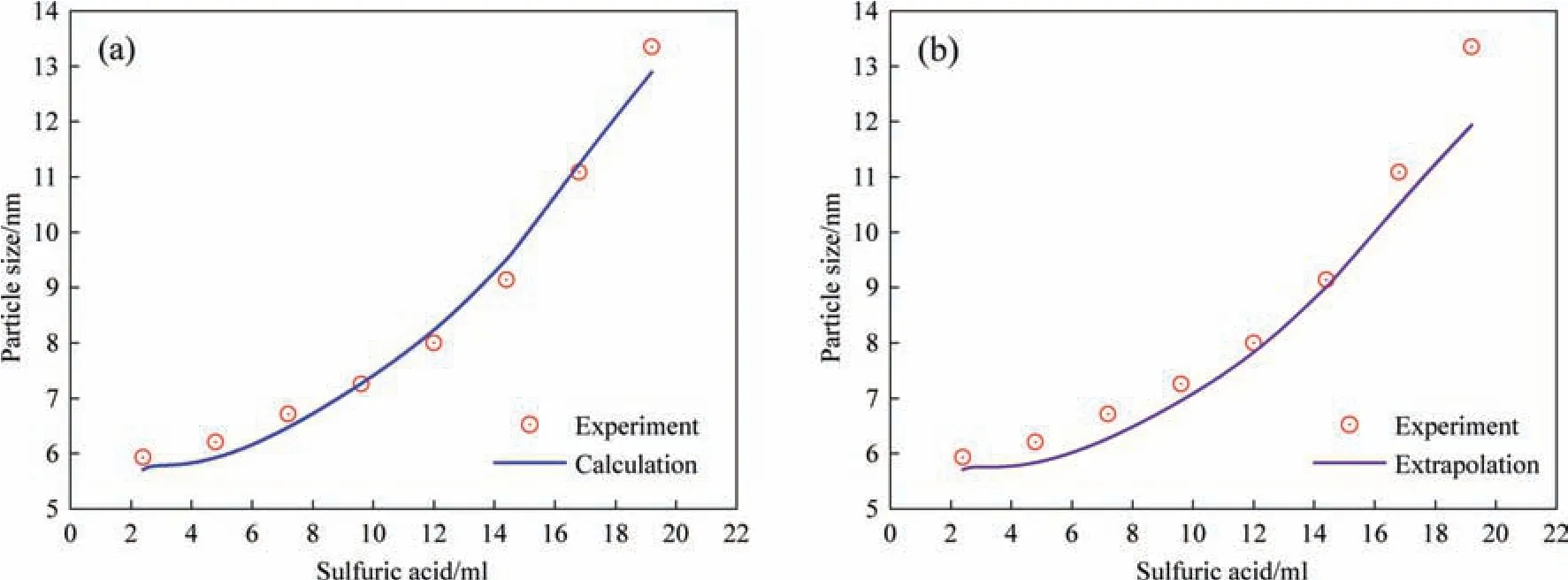
Fig.11.Comparison of calculated growth curve of silica nanostructured particles with experimental data for the sulfuric acid dripping rate of 1.2 ml·min-1 using (a)fitting parameters and (b) extrapolation parameters.(Reaction temperature: 363 K).

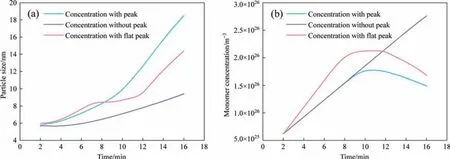
Fig.12.(a) Changes in particle growth rate with time and (b) the corresponding changes in monomer concentration.

The calculated values obtained from the proposed model were compared with the values obtained from experimental data.The simulations of the change in the particle size with time at different reaction temperatures and sulfuric acid dripping rates were in good agreement with the experimental data.The calculated growth curves corresponded with the two stages of the experiment.In addition,the particle formation process obtained by analyzing the change in the particle size distribution with time was also consistent with the experimental data.This indicated the reliability of the proposed nucleation-growth model.The proposed model was used to calculate the change in the mass transfer rate and surface reaction rate with time during the growth of silica nanostructured particles.The results revealed that the mass transfer process and surface reaction process alternately controlled the growth of the silica particles.The mass transfer is the ratedetermining step in the first stage,and the surface reaction controls the growth of silica particles in the second stage.The particle size calculated without considering the surface reaction was larger than the particle size obtained from experimental data.Moreover,three fitting parameters that cannot be obtained directly,namely,the activity coefficient,diffusion coefficient,and exponent in the power correction,were also investigated.Their physical implications and the effects of the temperature and sulfuric acid dripping rate on these three parameters were studied,respectively.The results show that the temperature had a significant effect on the activity coefficient and diffusion coefficient,and the diffusion coefficient increased with an increase in the acid dripping rate.However,the surface roughness of the particles did not change,irrespective of the reaction temperature or acid dripping rate.These three parameters were interpolated and extrapolated under different conditions,and the interpolated/extrapolated values were used to calculate the model.The calculated values were also close to the values obtained using experimental data.This revealed the reliability and the predictive ability of the proposed model.Finally,the relationship between the particle growth rate and the change in the monomer concentration was analyzed using the proposed model.The monomer concentration altered the growth rate by changing the nucleation and mass transfer rates.Moreover,the growth rate determined the monomer concentration by varying the monomer consumption.The non-ideality of the solution is a key factor linking the monomer concentration to the nucleation and growth rate.The proposed model provides a strong foundation for further research into the nucleation and growth process of precipitated silica nanostructured particles.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was financially supported by the National Natural Science Foundation of China (21878169,21991102),the National Key Research and Development Program of China(2019YFA0905100),and the Tsinghua University Initiative Scientific Research Program (2018Z05JZY010).