Dynamic polarizabilities of the clock states of Al+
Yuan-Fei Wei(魏遠飛) Zhi-Ming Tang(唐志明) Cheng-Bin Li(李承斌) Yang Yang(楊洋)Ya-Ming Zou(鄒亞明) Kai-Feng Cui(崔凱楓) and Xue-Ren Huang(黃學人)
1State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China
2Shanghai EBIT Laboratory,Key Laboratory of Nuclear Physics and Ion-Beam Application(MOE),Institute of Modern Physics,Fudan University,Shanghai 200433,China
3University of Chinese Academy of Sciences,Beijing 100049,China
4Key Laboratory of Atom Frequency Standards,Innovation Academy for Precision Measurement Science and Technology,Chinese Academy of Sciences,Wuhan 430071,China
Keywords: dynamic polarizability,Al+optical clock
1. Introduction
Optical frequency standards have important application prospects in local timekeeping,deep space satellite navigation and the test of the fundamental theory of physics.[1–4]In recent years,the optical frequency standards based on neutral atoms or trapped ions have made great development[5–9]and some of them have demonstrated fractional frequency uncertainties of a few parts in 10?18or even 10?19. Among them,the Al+optical clock based on the trapped Al+ion has been well developed in the past decades due to the application of the sympathetic cooling and quantum-logic technologies.[10]In 2010,NIST researchers realized the comparison of two aluminum ion optical clocks and the frequency uncertainty reached 8.6×10?18.[11]They improved their experimental setups in 2019 and achieved the systematic uncertainty of 9.4×10?19.[9]
The Al+optical clock is working on the highly forbidden 3s21S0–3s3p3Po0transition and the black-body radiation(BBR)shift of this transition is predicted to be very small.[12]Not only the intrinsic characters of Al+,which are insensitive to environmental perturbations,but also the delicate technologies of sympathetic cooling and quantum logic spectroscopy,make the Al+optical clock capable of achieving extreme precisions. To provide the reliable systematic uncertainty budget for the Al+optical clock, all the perturbations to the clock transition should be carefully considered, including the motional effects of the working ions, BBR shift of the clock transitions, frequency shifts due to the external electromagnetic fields,and so on. The BBR shift is generally associated with the differential static polarizabilities of the clock working states.[13]In the Al+clock,Mg+or Ca+is usually adopted for the sympathetic cooling of Al+.[9,11,14]The Doppler cooling laser beam of Mg+or Ca+maintains the Al+–Mg+or Al+–Ca+pair at a constant motional temperature during the clock interrogation pulse. Because it is also shed on the Al+ions,it causes an ac Stark shift to the clock transition,which is associated with the differential dynamic polarizabilities of the clock working states.
The polarizability of an atomic system describes the distortion in the charge distribution and gives a measure of the energy shift of the atomic system when it is exposed in an electromagnetic field.[12,15]Since precise measurement of polarizabilities is quite challenging,the reliable and accurate theoretical studies of atomic and ionic polarizabilities are of particular interest. In the case of Al+, the previous studies are mainly focused on the static polarizabilities[16–19]to evaluate the BBR contribution to the fractional frequency uncertainty of the clock transtion. Rosenbandet al.used an extrapolation expression to estimate the dynamic polarizabilities of the 3s21S0and 3s3p3Po0states of Al+at the wavelengthλ=1126 nm.[20]Although their results agreed with the later theoretical calculations using the configuration interaction plus core polarization (CICP) method[16]and the configuration interaction plus all-order(CI+all-order)method,[18]the wavelength of the electromagnetic radiation adopted in the extrapolation method is required to be far-detuned from all transitions connecting to either clock states. The study on the dynamic polarizabilities over large range of electromagnetic spectrum of Al+is still scarce. Such study would not only be useful in the potential experiments based on Al+, but also lead to the prediction and identification of the magic wavelengths of Al+clock transition. The magic wavelength for a transition is the wavelength at which the ac Stark shift of the transition energy is zero,[21]and it means that, for the upper and lower energy levels of the transition concerned, the difference of the dynamic polarizabilities is zero. A notable application of the magic wavelengths is the optical lattice clocks operated on the neutral atoms.[1]As for the atomic ions, the magic wavelengths for the 4s1/2–3d5/2transition in Ca+have been observed,and meanwhile the ratio of the matrix elements for the 4s1/2–4p1/2and 4s1/2–4p3/2has been determined.[22]The identification of magic wavelength for ion clock transition pave the milestone for establishing all-optical trapped ion clocks and the precision values of the transition matrix elements extracted from the magic wavelength measurement could be used to improve the precision of the estimation of the BBR shift.
For these motivations, we made calculations of the dynamic polarizabilities of the 3s21S0and 3s3p3Po0states in Al+based on sum-over-states (SOS) approach. The transition matrix elements were obtained using the method combining configuration interaction and the many-body perturbation theory(CI+MBPT),[23]and the multiconfiguration Dirac–Hartree–Fock (MCDHF) method.[24]A brief introduction of the theoretical methods and computational details is given in Section 2. The computation results of the energy levels,transition matrix elements,polarizabilities and magic wavelengths are given and discussed in Section 3.
2. Method of calculations
2.1. Polarizability
The dynamic electric dipole(E1)polarizability of a quantum stateνin an electromagnetic radiation generally consists of three contributions from scalar, vector and tensor polarizabilities.[25]Both contributions from vector and tensor polarizabilities are related with the magnetic angular momentum quantum numbers of the atomic state. In this work,3s21S0and 3s3p3Po0states in Al+will be considered,and total angular momentum quantum numbersJfor both states are zero. Thus, only the scalar polarizability will be taken into account,and it can be conveniently divided into three parts:

whereIis the laser intensity, andO(I2) represents the residual high-order Stark shift which is usually small and can be omitted under the weak intensity limit. The frequency shift of a certain transition caused by the electromagnetic field can be written as

where ?α(ω) is the differential dynamic polarizability of statesκandν. Thus, by ignoring all nonlinear Stark shifts,the magic wavelength can be theoretically given by the condition ?α(ω)=0.[1]
2.2. CI+MBPT calculations
In the present work, CI+MBPT calculations are performed to get the energy levels and RMEs for Al+using the program package developed by Kozlovet al.[23]The CI+MBPT method is based on a combination of a conventional configuration interaction (CI) method and many-body perturbation theory (MBPT). The former explicitly contains the interaction between valence electrons, while the latter includes core–core and core–valence correlations. The calculations start from the numerical solution of Hartree–Fock–Dirac(HFD)equations using finite difference method to get singleelectron HFD energies and wavefunctions for the core and valence electrons. Here, 1s–4s, 2p–4p, 3d–4d and 4f orbitals are taken into account in this step. The virtual orbitals are then constructed by an automatic generation subroutine which is embedded in the package. The maximal principal quantum numbernmaxand the maximal orbital quantum numberlmaxare set to be 30 and 4, respectively. The HFD orbitals and the auto-generated virtual orbitals form the basis set (or say,the orbital space)for the later CI and MBPT calculations.The electron configuration of Al+can be treated as a closeshell core [1s22s22p6] and two valence electrons outside the core. The effective Hamiltonian for two valence electrons in the CI+MBPT method can be written as

where ?h1and ?h2are the single-electron and two-electron interaction terms of the relativistic Hamiltonian, respectively.In the standard CI method, ?h1includes the kinetic energy of the electron, Coulomb interaction with the nucleus and the HFD potential of the close-shell atomic core. The CI space is formed by a set of configuration with all possible single(S)and double(D)excitations of the valence electrons in a given basis set. We first set the basis set of orbitals as{16s, 16p,16d,16f,16g},and then increase it up to{26s,26p,26d,26f,26g}and{29s, 29p, 29d, 29f, 29g}, which leads to the energy change with the expansion of the CI space lower than 0.01% and the matrix elements of the allowed E1 transitions change at most 0.03%. ?h2is the interaction between the valence electrons. In the CI+MBPT procedure,a single-electron operator which represents the correlation interaction of a particular valence electron with the atomic core is added into ?h1.A two-electron operator which represents the screening of the Coulomb interaction between the two valence electrons by the core electrons is added into ?h2. Both additional operators are treated in the second order of MBPT.
2.3. MCDHF calculations
To verify the hybrid CI+MBPT calculations,the MCDHF method is used in this work,as it is another form of CI method and based on the variational principle with both expansion coefficients and the orbitals to be variational parameters so that take into account correlations in a different way. The MCDHF calculations in this work are performed using the GRASP2018 package.[24]
In the MCDHF method, the calculation starts with the many-electron Dirac–Coulomb Hamiltonian

whereciis expansion(mixing)coefficient,γistands for the remaining quantum numbers of the CSFs. Each CSF is a linear combination of products of one-electron Dirac orbitals.Both mixing coefficients and orbitals are optimized in the selfconsistent field calculation. After a set of orbitals is obtained,the relativistic configuration interaction(RCI)calculations are used to capture more electron correlations. In addition to the Coulomb interactions, our RCI calculations also include the Breit interaction in the low-frequency approximation and the quantum electrodynamic(QED)corrections.
In the present MCDHF calculations, the CSF space of a specifiedPandJsymmetry is generated following the active set(AS)approach[27,28]by virtual excitations from the orbitals in multireference (MR) configurations to an active set of orbitals. By extending the AS systematically, the CSF space is increased and thereby approaches the complete representation of the ASF with Eq.(7). The ASFs of even and odd states are optimized separately and the MR configuration sets for even and odd parities include

Initial MCDHF calculations in the RSCF procedure are performed to determine simultaneously all the orbitals of the MR sets without any excitations. Subsequently,the CSFs expansions are obtained through single and double excitations from the orbitals in the MR sets of configurations up to an AS of orbitals withn ≤13,l ≤4. The AS is increased with layer by layer in 8 steps fromn=6 up to 13,i.e.,AS1–AS8,so that the basis set convergence in the calculations can be demonstrated.In each step,only the orbitals in newly added layer are optimized and the other orbitals are kept to be fixed. We treat the orbitals withn ≤2 as the core,and the other orbitals as the valence orbitals. We have allowed single and double excitations from the valence orbitals and single excitations from the core so that both the valence–valence(VV)and core–valence(CV) correlations have been taken into account in the RSCF procedure. In our test calculations,it was found that the contributions from 1s and 2s excitations are not important to the atomic parameters concerned, so these orbitals are kept to be fixed as an inactive core in the final calculational model. The differences between the energy levels obtained with the last two basis set, AS7and AS8, do not exceed 15 cm?1for any level.
Here we also include higher-order correlation effects with a further extended CSF space enlarged by allowing triple (T)excitations from the orbitals in the MR sets to an ASi(i ≤5)of orbitals obtained in the previous RSCF procedure. It is convenient to define the CSF space in each step of SD-excitations as sdASi(i ≤8) and in each step of SDT-excitations as sdAS8+triASi(i ≤5). The differences between the energy levels obtained with sdAS8+triAS4and sdAS8+triAS5do not exceed 10 cm?1for any level. Therefore, the ASFs for every atomic states concerned are finally expanded with the CSF space sdAS8+triAS5by Eq.(7).
Once the ASFs are obtained,the multipole-radiative transition matrix element from an initial stateΨ(γPJM)to a final stateΨ(γ′P′J′M′),〈Ψ(γPJM)‖?O(k)‖Ψ(γ′P′J′M′)〉can be obtained.
3. Results and discussion
3.1. Energy levels and E1 matrix elements
In the present work, the energy levels and the E1 transition matrix elements of Al+are calculated using CI+MBPT method and MCDHF method. The computational details of each method are described in Section 2. The results of the excitation energies from the ground 3s21S0state to the low-lying states of Al+obtained using CI+MBPT method with the basis set{29s,29p,29d,29f,29g},and using MCDHF method with sdAS8+triAS5are tabulated in Table 1. It includes 16 odd-parity states with 3s3p, 3s4p, 3s4f and 3s5p configurations, and 17 even-parity states with 3p2, 3s4s, 3s3d, 3s5s,and 3s4d configurations. The final results of both CI+MBPT and MCDHF methods show good agreement with the values listed in National Institute of Standards and Technology(NIST)database.[29]It is noted that the discrepancies between the results of CI+MBPT method and NIST data are below 124 cm?1and the relative deviation to NIST data is lower than 0.13%.The energies of CI+MBPT method using pure CI,CI+MBPT without and with Breit interaction procedures are presented. It shows that the combination of CI and MBPT improves the accuracy notably. Although the double excitations from core orbitals are neglected in our MCDHF calculations,the discrepancies between the calculated excitation energies and NIST data are below 400 cm?1and the relative deviation to NIST data is lower than 0.4%. This shows the importance of the VV and CV correlations in the MCDHF calculations on the transition properties of Al+.The contributions of the triple excitation,Breit interaction,self-energy and vacuum polarization to the final MCDHF results are also listed in the table.
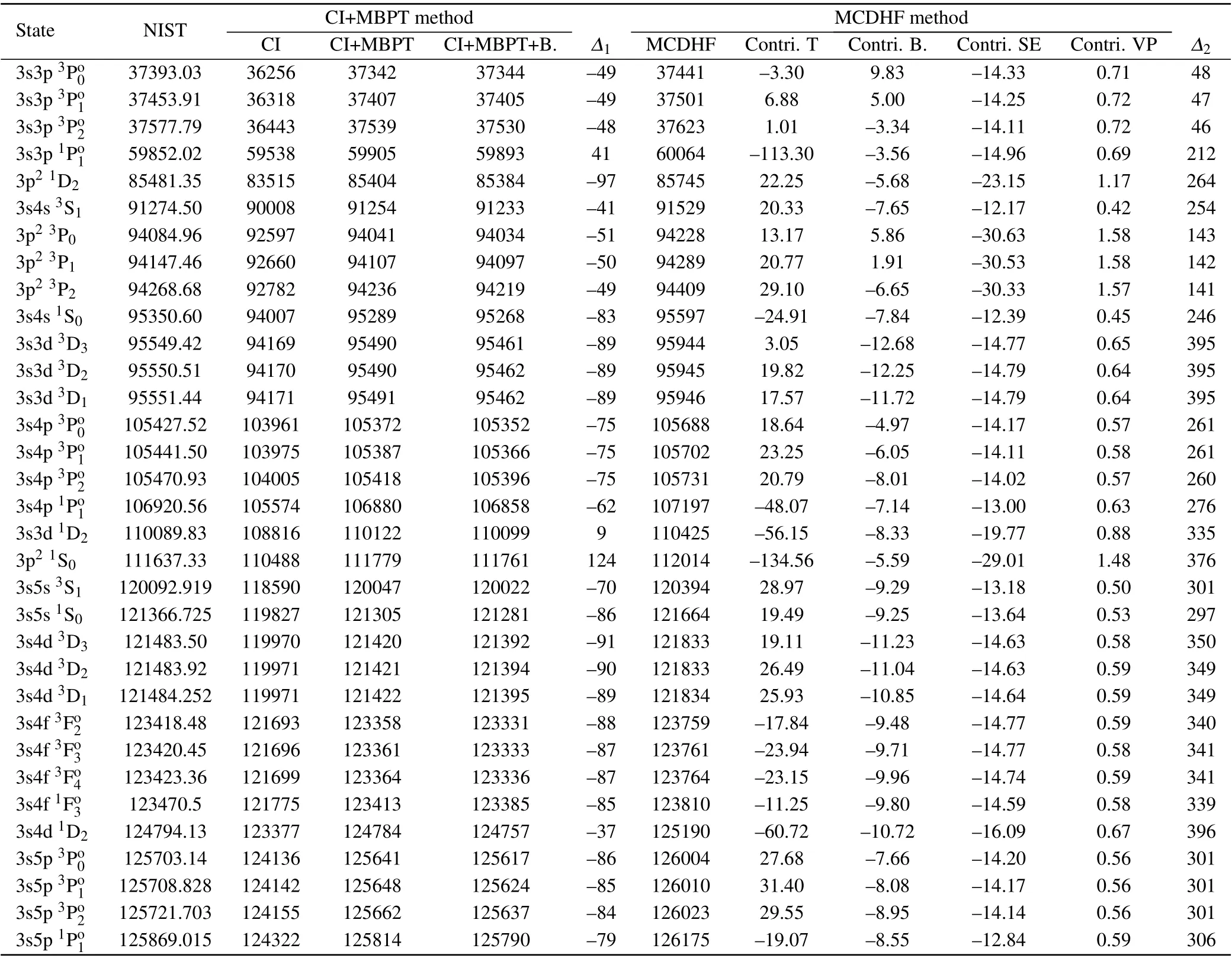
Table 1. The excitation energies(in cm?1)of the low-lying levels of Al+, obtained by using the CI+MBPT and MCDHF methods and compared with the available values listed in NIST database.[29]T,B.,SE and VP denote the triple excitation,Breit interaction,self-energy and vacuum polarization,respectively.?1 ≡ECI+MBPT+B.?ENIST and ?2 ≡EMCDHF ?ENIST.
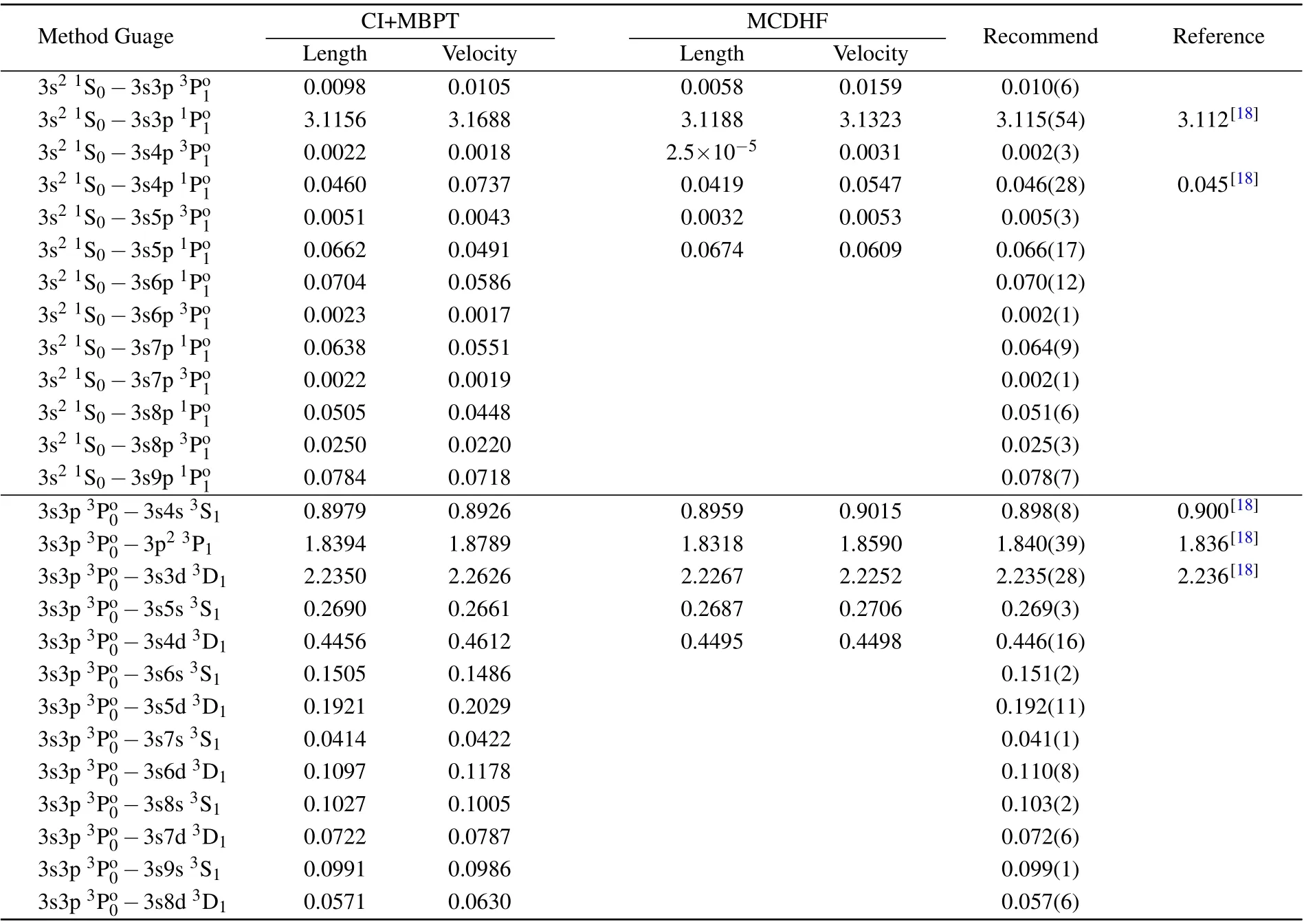
Table 2. The reduced matrix elements of E1 transition for the 3s21S0 and 3s3p3Po0 clock states of Al+,obtained by using the CI+MBPT and MCDHF methods.
The E1 RMEs involving the 3s21S0and 3s3p3Po0clock states of Al+obtained using CI+MBPT and MCDHF methods are presented in Table 2. The results in both length and velocity gauge are listed. The CI+MBPT results in the length gauge agree well with the counterparts obtained using CI+allorder method.[18]The E1 RMEs involving 3s3p3Po0state of CI+MBPT and MCDHF method in the same gauge have good agreement with each other,and the relative differences are below 2%. The agreement of the E1 RMEs involving 3s21S0state of both methods in the same gauge is not as good as the E1 RMEs involving 3s3p3Po0state and the relative differences span from 0.1% to over 50%. However, we would like to emphasize here that large discrepancies only occur for those RMEs involving weak transitions,which contribute fractionally to the polarizabilities discussed in this work. The discrepancy in the length and velocity gauge of E1 RMEs can be noted for the same theoretical method. Although it can be shown that the length and velocity form of the electric multipole transition operators yield the same line strength for an exact solution in the non-relativistic theory, it is not exactly same in the relativistic Dirac theory.[30,31]It is pointed out that the discrepancies in the length and velocity gauge of the calculated line strengths(SOνκ=|〈ν‖?O‖κ〉|2)for E1 transition is an important uncertainty indicator.[31,32]Thus, we also give the recommended values of E1 RMEs in Table 2, and the uncertainties are given following the above suggestion.
3.2. Polorizabilities
The static and dynamic E1 polarizabilities are calculated using Eqs.(1)and(2). The transition energies used in Eq.(2)are cited from NIST data. For the choice of the static polarizability of Al3+core,αcore, Mitroyet al.adopted the value of 0.268 a.u. which is the scaled result obtained from a perturbed HF calculations[16]and Safronovaet al.adopted 0.265 a.u.in their evaluation the BBR shift of the clock transition in Al+using CI+all-order method.[18]We apply the coupled-cluster method with single and double excitations (CCSD) which is implemented in Gaussian09 package[33]associated with a large basis set (aug-cc-pv6z basis set) and get 0.260 a.u. for the Al close-shell core. This result should capture sufficient correlation contribution, but the relativistic effect is absent.In the present work,αcore=0.265(5) a.u. is adopted. Corevalence contributions to the polarizability is usually small,and they are cited from Ref.[18]with a“safe”uncertainty of 50%.The dynamic corrections toαcoreandαcvfollow the extrapolation method used by Breweret al.[9]Static E1 polarizabilities for 3s21S0and 3s3p3Po0states are listed in Table 3. The SOS method is adopted for the polarizability calculations in this work. Our calculated values for the static polarizabilities agree with the results from other theoretical work. The uncertainties for the calculated static polarizabilities come from the uncertainties of the E1 RMEs,core and core-valence contributions. The present differential polarizability also agrees with the experimental result,[9]which is derived from the ac Stark shift measurement using an extrapolation method.
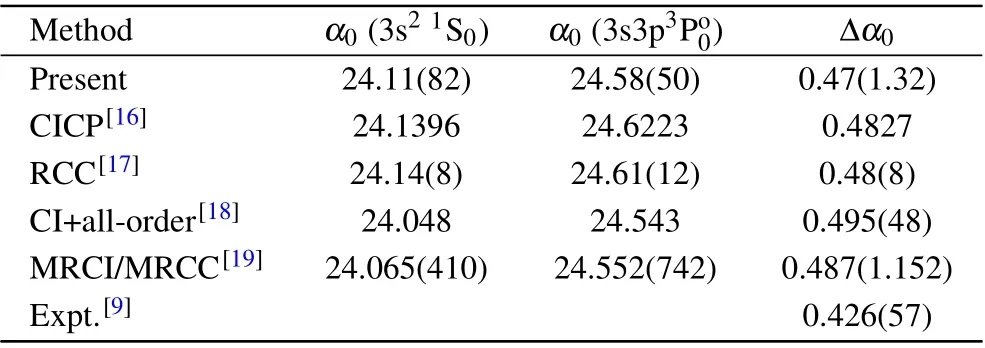
Table 3.The static E1 polarizabilities(in a.u.)of 3s21S0 and 3s3p3Po0 states in Al+,and the differential polarizabilities.
The dynamic polarizabilitiesα(ω) of the 3s21S0and 3s3p3Po0states in Al+are shown in Fig. 1. The photon energies of the electromagnetic radiation from 0 to 0.43 a.u.are taken into account, which is equivalent to the wavelength varying from ∞down to 106 nm. Five magic wavelengths of the Al+3s21S0–3s3p3Po0clock transition are identified, as 267.01(10) nm, 183.18(2) nm, 173.68(2) nm, 120.50(2) nm,and 113.33(48)nm. All magic wavelengths are located in the ultraviolet region. In the our numerical procedures,the magic wavelength is obtained when the dynamic differential polarizability ?α(ω)of 3s21S0and 3s3p3Po0states is zero. It can be noted that the core polarizability is same for both clock states and it will not affect the position of the magic wavelength.The uncertainty of the magic wavelength is evaluated by taking account of the uncertainties of the E1 RMEs in the magic wavelength identification procedure.
The contributions of individual transitions to the static and dynamical polarizabilities of the 3s21S0and 3s3p3Po0states at the magic wavelengths for the 3s21S0–3s3p3Po0clock transition in Al+are tabulated in Table 4. It is noted that the contribution of 3s21S0–3s3p1Po1transition solely dominates the static and the five dynamic polarizabilities of 3s21S0state at the magic wavelengths, and it contributes no less than 92%. For the static and dynamic polarizabilities of 3s3p3Po0state at three magic wavelengths (267.01 nm,183.18 nm and 173.68 nm), the contributions of three transitions, 3s3p3Po0–3s4s3S1, 3s3p3Po0–3p23P1, and 3s3p3Po0–3s3d3D1, are over 95%. Tanget al.suggested that the ratio of two oscillator strengths could be determined via the precision measurement of magic wavelength for Ca+,[34]and it was practiced successfully.[22]By taking similar procedure in Ref. [22] and taking into account the RME of the strongest E1 transition 3s21S0–3s3p1Po1, the measurement on the magic wavelengths of Al+clock transition at 267.01 nm, 183.18 nm, and 173.68 nm would be helpful to obtain three ratios of the E1 RMEs for the four transitions mentioned above, RME(3s21S0–3s3p1Po1):RME(3s3p3Po0–3s4s3S1), RME(3s21S0–3s3p1Po1):RME(3s3p3Po0–3p23P1),and RME(3s21S0–3s3p1Po1):RME(3s3p3Po0–3s3d3D1). It can act as a calibration with the experimental input to the calculated RMEs,and then improve the reliability and the precision of the estimate of the BBR shift for the clock transition.
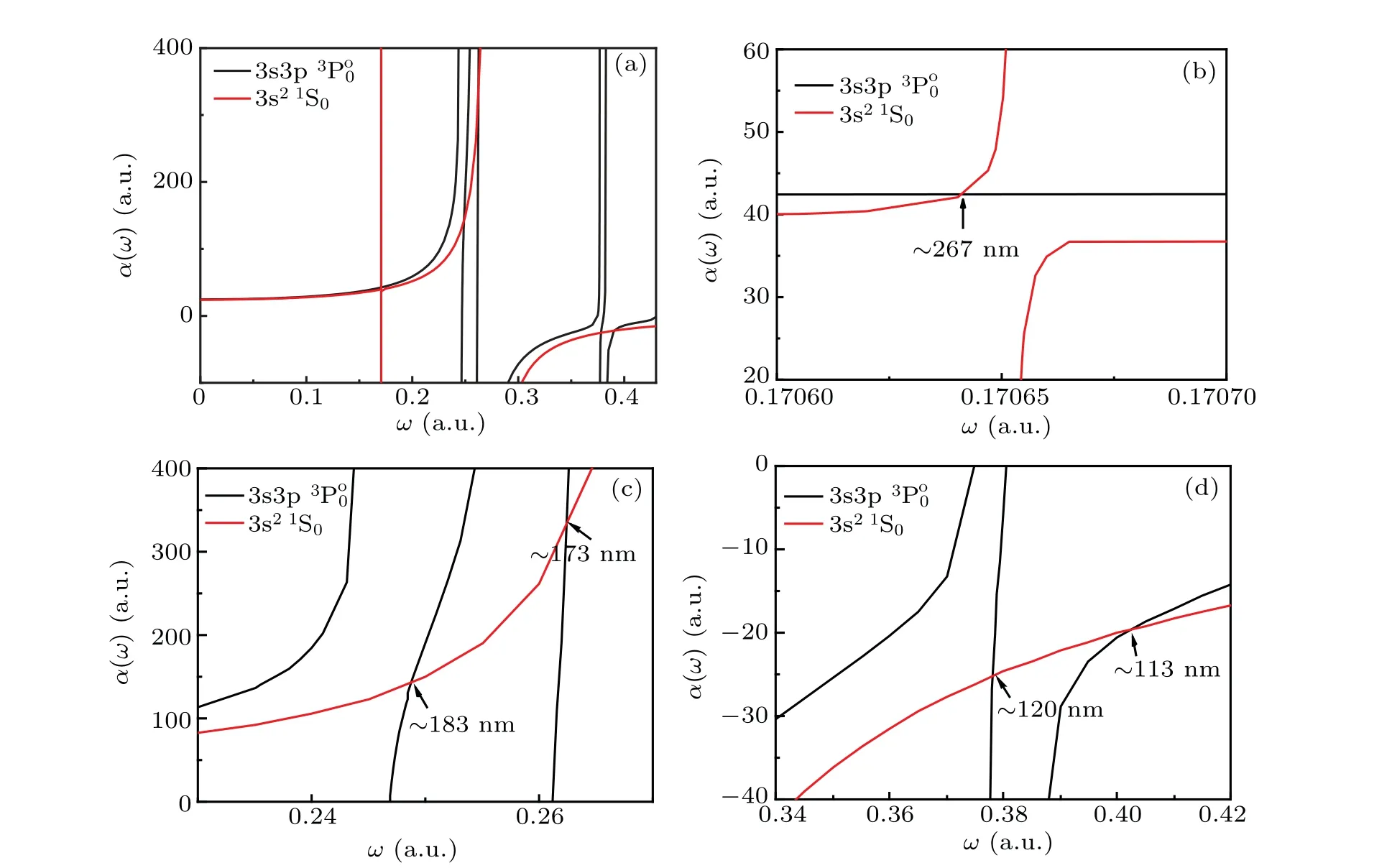
Fig.1. The dynamic polarizabilities α(ω)of the 3s21S0 and 3s3p3Po0 states in Al+,in a photon energy of the electromagnetic radiation from 0.0 to 0.43 a.u.,which is equivalent to the wavelength from ∞down to 106 nm. The magic wavelengths are identified by arrows in(b)–(d).
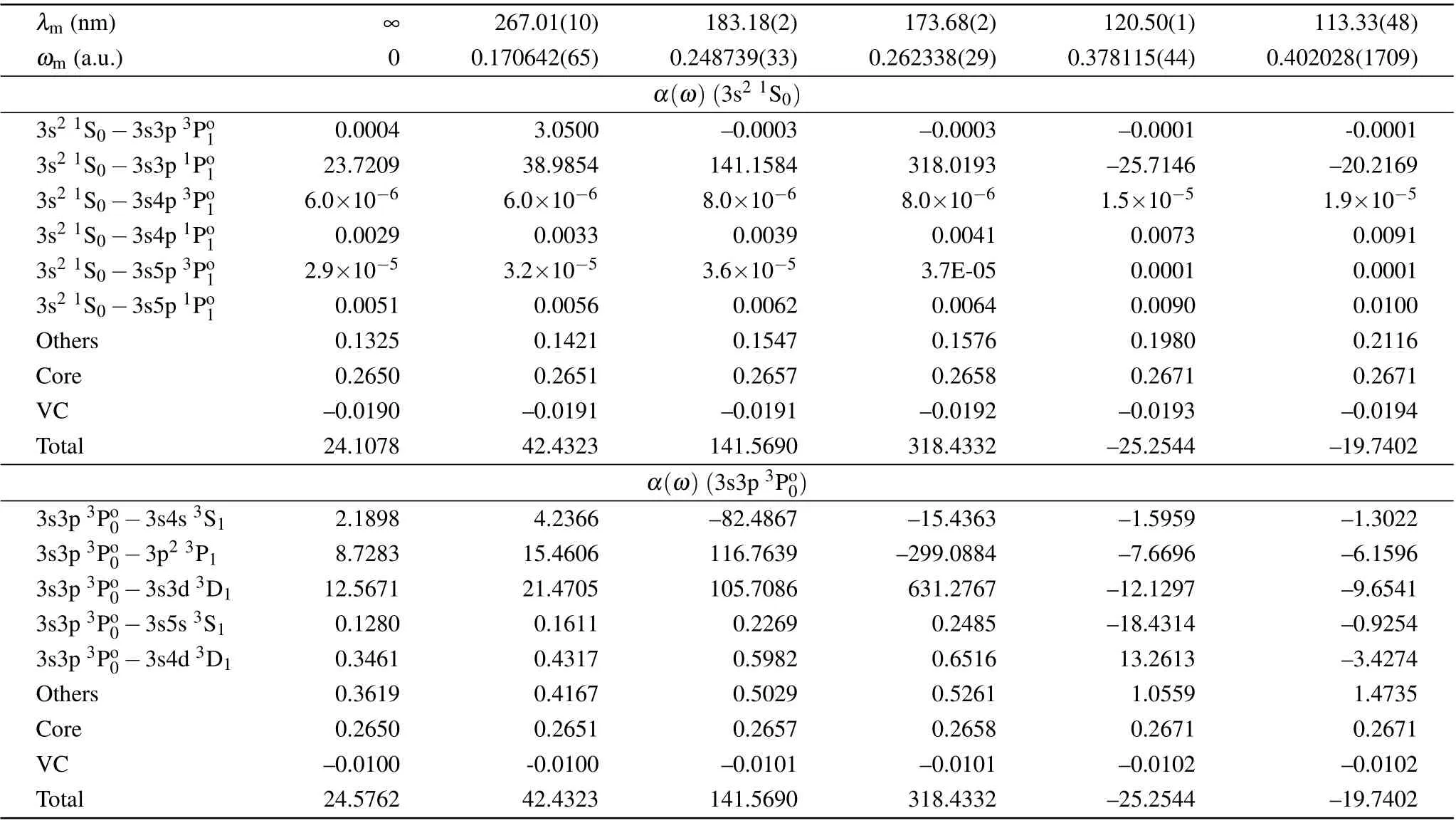
Table 4. The breakdown of the contributions of individual transitions to the static and dynamical polarizabilities of the 3s21S0 and 3s3p3Po0 states at the magic wavelengths for the 3s21S0–3s3p3Po0 clock transition in Al+. The numbers in parentheses are uncertainties in the digits calculated by adopting the recommended uncertainties of E1 RMEs in the present work.

Table 5. The differential dynamic polarizabilities(in a.u.) of the clock states in Al+.
The calculated dynamic polarizabilities can be used to evaluate the ac Stark shifts due to the clock interrogation,cooling,and repumping laser beams of the Al+optical clock.Based on the knowledge of the dynamic prolarizabilities obtained in this work, the calculated differential polarizabilities of the Al+clock transition at several specific wavelengths are given in Table 5. Rosenbandet al.measured the ac Stack shift of the Al+clock transition using an infrared light at 1126 nm[20]and obtained ?α(ω)=1.08(34)a.u.CI+all-order method gives this value as 0.549(55) a.u. and CICP method gives as 0.54(41)a.u. Our result agrees with theirs. Breweret al.obtained ?α(976 nm)=0.499(57)a.u.in their experiment and our result also agree with it. The wavelength of the clock interrogation beam is 267.4 nm. The cooling (397 nm) and repumping beams (866 nm) are kept on in same experiments to maintain a stable cooling.[35]According to the data in Table 5 and assuming all the laser beams to be Gaussian beams,the contributions of ac Stark shift to the fractional frequencey shift (?νac-Stark/νclock) of Al+clock transition at 267.4, 397 and 866 nm are (1.54±1.21)×10?20?I, (5.74±8.61)×10?20?I,and(2.98±7.28)×10?21?I,respectively,where the effective intensity ?I=P/r2,Pis the power of the laser in units of W andris the radius of beam waist in units of m.
4. Conclusions
In summary, the dynamic polarizabilities of 3s21S0and 3s3p3Po0states in Al+are calculated using CI+MBPT and MCDHF methods in this work. The magic wavelengths for the Al+clock transition 3s21S0–3s3p3Po0are identified. All the magic wavelengths predicted in this work are in the ultraviolet region. The potential precision measurement on these magic wavelengths of Al+near 267 nm,183 nm and 173 nm would be useful to extract the ratios of several certain transition matrix elements with high accuracy,and then to improve the precision of the estimate of the BBR shift for the Al+clock transition. The differential dynamic polarizabilities at certain wavelengths are evaluated using the knowledge of the calculated dynamic polarizabilities, which are useful to assess the ac Stark shift of the Al+clock transition frequency and helpful in the clock experiments to suppress the ac Stark shift of the clock transition as possible as it can.
Acknowledgements
The authors would like to thank Professor M. G. Kozlov and Dr. Y. M. Yu for the helpful assistance on the use of CI-MBPT package. This work was supported by the National Natural Science Foundation of China (Grant Nos. 11934014, 11904387, 11704076, and U1732140), the National Key Research and Development Program of China(Grant Nos. 2017YFA0304401 and 2017YFA0304402), and Technical Innovation Program of Hubei Province, China(Grant No.2018AAA045).
- Chinese Physics B的其它文章
- Magnetic properties of oxides and silicon single crystals
- Non-universal Fermi polaron in quasi two-dimensional quantum gases
- Purification in entanglement distribution with deep quantum neural network
- New insight into the mechanism of DNA polymerase I revealed by single-molecule FRET studies of Klenow fragment
- A 4×4 metal-semiconductor-metal rectangular deep-ultraviolet detector array of Ga2O3 photoconductor with high photo response
- Wake-up effect in Hf0.4Zr0.6O2 ferroelectric thin-film capacitors under a cycling electric field

