Jin Xu(徐瑾), Xiaoguang Chen(陳曉光), Rong Zhang(張蓉), and Hanwei Xiao(肖晗微)

Department of Communications Science and Engineering,Fudan University,Shanghai 200433,China

Keywords: purification,quantum neural network,entanglement distribution,quantum communication

1. Introduction

Entanglement distribution occupies an important role in quantum communication. It helps people to realize communication with the help of entanglement. In 1992,Bennett and Wiesner proposed dense coding to encode classical information into pre-shared entangled states to expand the channel capacity and protect the information from eavesdropper.[1]Mattle and his team experimentally realized it.[2]And this technology is widely used in quantum key distribution.[3]Entanglement is not only used to transfer classical bits in dense coding,but also helps to realize arbitrary quantum state transmission in teleportation. In 1993,Bennett proposed the first teleportation protocol based on Einstein–Podolsky–Rosen(EPR)states after entanglement distribution.[4]Bouwmeester proved it in the practical experiment.[5]

In recent years, scientists tried to realize long-distance entanglement distribution.[6,7]Finding the way to overcome noise in channel is still the focus in quantum communication.Ecker and his team showed the challenges and benefits of using high-dimensional states in their experiment.[8]High dimension can increase the noise resistance of entanglement,but also bring extra noise. To solve the noise in entanglement distribution, two commonly used technologies in quantum communication are entanglement purification and quantum error correction coding.[9]Purification works as a fast quantum state screening mechanism, while error correction coding attempts to consume amounts of basic states to encode one quantum state and protect it. Since there is no valuable information transferred in entanglement distribution, purification is more appropriate in this scenario for its lower computational complexity. Thus, purification has been widely applied on entanglement distribution with low dimension.[10,11]D¨ur and his team keep working in this field to find the better purification protocol.[12–14]They tried to control the purification strategy based on the known channel environment to improve the fidelity. Besides, they also used high-dimensional entangled states to improve the fidelity of state with lower dimension.However, channel environment is hard to accurately predict.And entangled states with high dimension consume huge number of basic states. What is more, they also bring more noise because of the higher dimension.

In 2020,Kerstin and his team tried training deep quantum neural networks.[15]They proposed a true quantum analogue of classical neurons,which forms quantum feed forward neural network. In their method, the number of required qubits scales with only the width, which allows deep-network optimization. People can use this quantum neural network to train the model of unitary operator overcoming noise in the environment.

In this paper,fidelity of entangled states is calculated under different quantum noises. We use depolarizing noise to represent unitary noise,and amplitude damping noise to represent non-unitary noise in channel.We find that purification can improve the fidelity in a larger domain with the help of QNN.To verify it in true environment, we finish the simulation on Cirq. The mixed scheme can surely bring higher fidelity without consuming more entangled states. Besides,it also helps to get fidelity gain from increasing dimension under non-unitary noise. Thus,it is of great value in the future commercial use.

The paper is outlined as follows. In Section 2, review the entangled states, quantum noise, fidelity, and general purification in entanglement distribution. In Section 3,combine purification and QNN during entanglement distribution under quantum noise. In Section 4, simulate the mixed scheme and analyze it in true environment on Cirq. Finally,conclusion is given in Section 5.

2. Preliminary

2.1. Entangled state

wherenis the dimension of state.|ψ〉is Bell state whenn=2,and isn-qubit GHZ state whenn>2.

An entangled state consists of amounts of qubits, which are entangled with each other.Different entangled states in the same dimension are mutual orthogonal. But in this paper,we only choose|ψ〉to realize entanglement distribution. Thus,we do not list forms of other entangled states.

2.2. Fidelity of state

Quantum state we finally get is usually different from the theoretical one. Fidelity is used to measure this deviation,defined in Ref.[16]

2.3. Noise in channel

During entanglement distribution,quantum noise can affect and even destroy the entanglement.[16]In this paper, we divide noise into unitary noise and non-unitary noise. When the noise is unitary,entangled states change but still keep entangled. When the noise is non-unitary, states do not keep entangled.

The most commonly used unitary noises are bit-flip noise,phase-flip noise,and depolarizing noise. We select depolarizing noise to represent unitary noise,because it is the mixed of different flip noises. Channel with depolarizing noise is

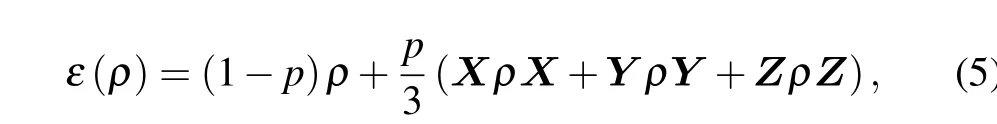
2.4. Purification in entanglement distribution

Assume the source node could generate entangled states with the fidelity of 1. Only part of states in an entangled group need to be transferred to the destination node in entanglement distribution. And the other part is held by the source node.Purification based on Bell state in entanglement distribution is shown in Fig. 1, which is studied in detail in our another work.[17]For an arbitrary quantum state,both waiting and being transferred in channel can be affected by noise.

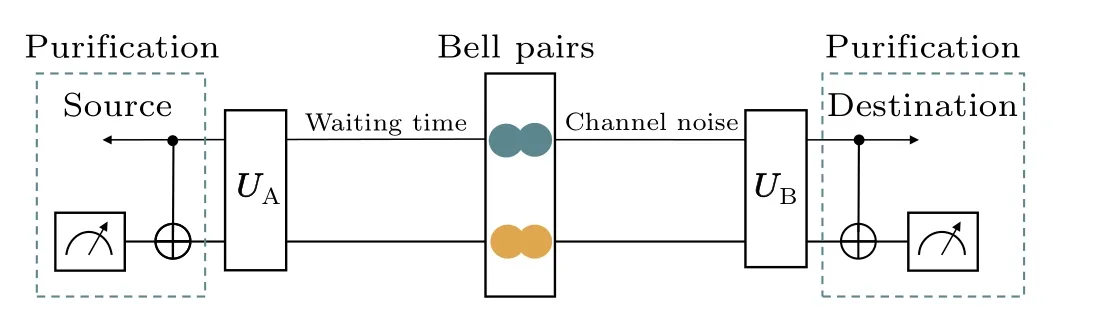
Fig. 1. Purification circuit based on Bell state in entanglement distribution.UA and UB are rotation operators. Blue color represents the control group,while yellow color represents the target group.

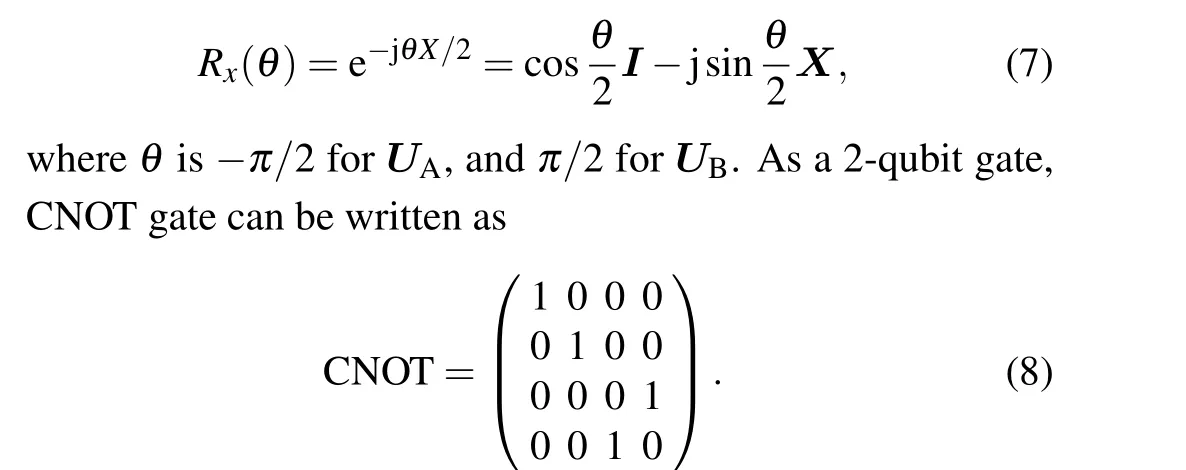
Purification circuit consists of rotation operators, CNOT gate and measurement device after entanglement distribution. Purification scheme with rotation operators comes from Deutsch’s work in 1996,which is called quantum privacy amplification(QPA)and used to solve both bit-flip and phase-flip noise in channel.[18]Rotation operators here can be written as For the CNOT gate,if the control qubit is|0〉,the target qubit remains unchanged. If the control qubit is|1〉,the target qubit will be bit flipped. Thus, in the purification circuit we divide entangled states into control group and target group. If the measurement results of qubits in target group equal to each other,the purification succeeds,and the control group will be stored in the device. Otherwise,the purification fails,and the control group will be discarded.

3. Purification with quantum neural network

Purification works in pumping manner[9]in the most time. Purification circuit with n dimension is shown in Fig.2,which can iterate on demand. Here we do not add rotation operators, because for entangled states with different dimensions,calculation shows that proper rotation operators not always exist.[17]The control group and the target group have been distributed under noise before purification. Only when measurement result of state in target group equals to each other, do we consider the purification to be successful and store the control group for the following communication task.Otherwise, we will discard the control group. Thus, purification works as a screening strategy for the state we want.

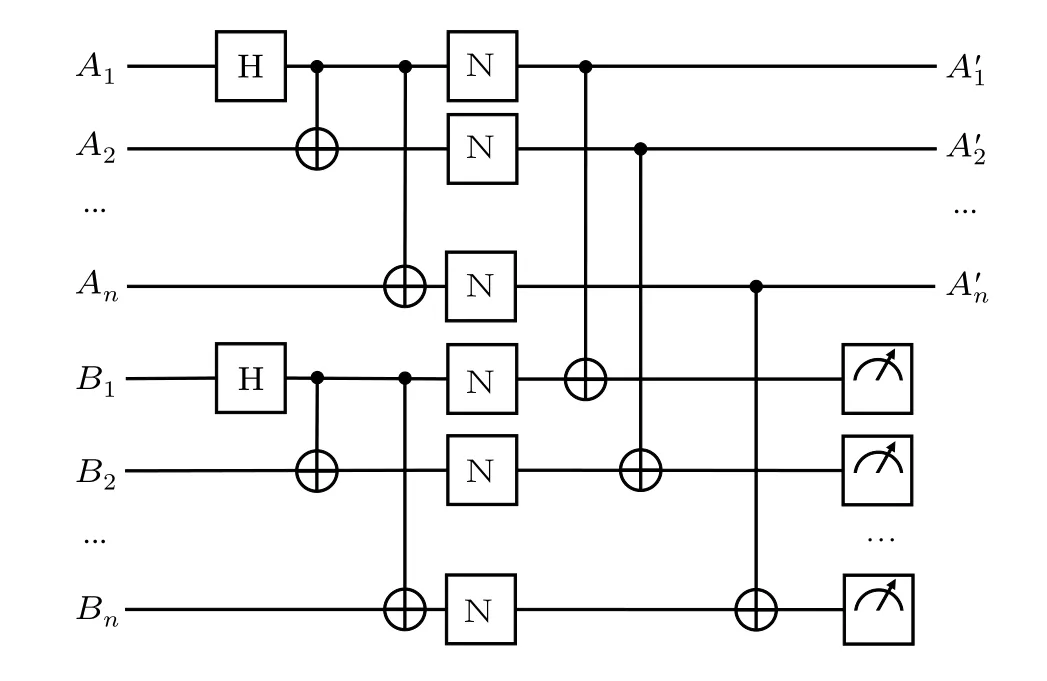
Fig. 2. Purification circuit with n dimension. A is the control group, while B is the target group. N is the noise. People can decide to store or discard A based on the measurement results of B.

Pumping manner helps purification to get higher fidelity by improving times of purification for one control group. But it consumes huge amounts of entangled states, especially purification does not always succeed. Finding a way to improve the fidelity without huge consumption is valuable. Thanks to Kerstin’s team, deep QNN can help to train unitary operators against noise,[15]if we have known the final desired output.

The smallest building block of QNN is the quantum perceptron, which is an arbitrary unitary operator at the beginning. We can train the network to obtain the proper unitary operator for the target state in an iterative way. Thus,QNN is a quantum circuit of unitary operators organized intoLhidden layers. It acts on the stateρinand produce the stateρout.

whereU=UoutULUL?1···U1is the circuit of quantum network we need to train.Ulis the layer unitary,which consists of the product of perceptrons in layerslandl ?1. Since perceptrons do not communicate in the network,the order of them is important as shown in Fig. 3. Layer unitary can be calculated layer-by-layer. So, we just need to calculate two layers at one time. This reduces algorithm complexity.

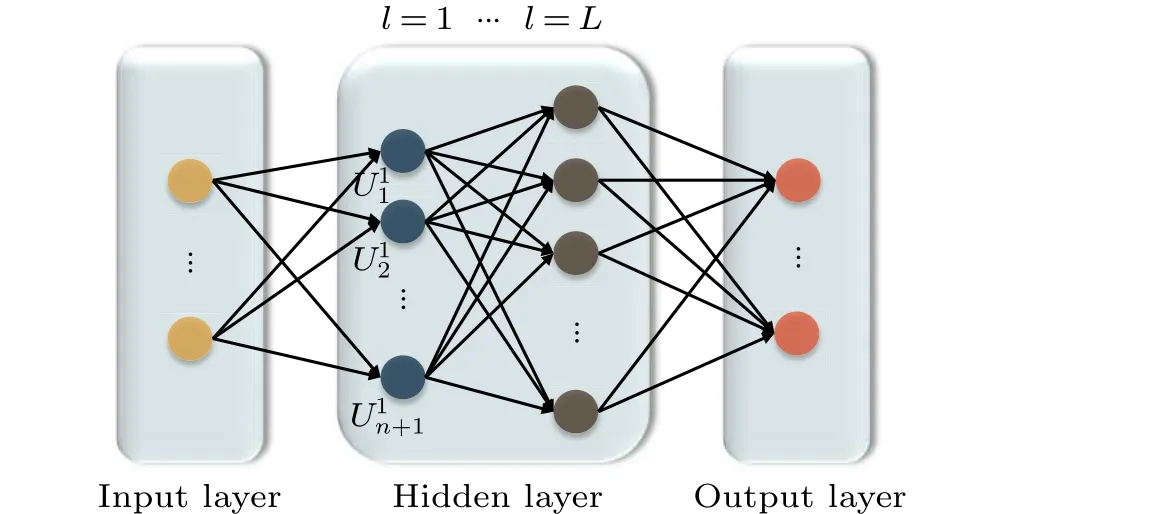
Fig.3. The architecture of quantum neural network. It has an input,output,and L hidden layers. Perceptron is applied from top to bottom in the layer.Assume the dimension of input layer is n.Thus,when l=1,the layer unitary U1=U1n+1···U12 U11.

The algorithm of training QNN is described in Ref.[15].Here we need to point out that the training mode of QNN network is different under different noise.Flip mode is chosen for unitary noise, while rotation mode is chosen for non-unitary noise. To measure the performance of QNN, cost function is given as

4. Simulation and analysis

To measure the performance of the mixed scheme, we simulate the quantum circuit on Cirq under true environment.Results are shown in Fig. 4. Compared with the initial entanglement distribution without optimization,both purification and QNN can improve the fidelity of entangled states. But their effective domains are different. Purification is effective for a good channel with little noise,while QNN is effective under heavy noise. The mixed scheme helps us to get the fidelity gain from both of them. But this combination is not simply splicing two independent performance curves of purification and QNN.Around the intersection of two performance curves,fidelity of the mixed purification scheme based on QNN circuit is improved to be the highest one. The reason is that this range lies in the effective domain of both two techniques, and thus appears as a superposition of different fidelity gains.

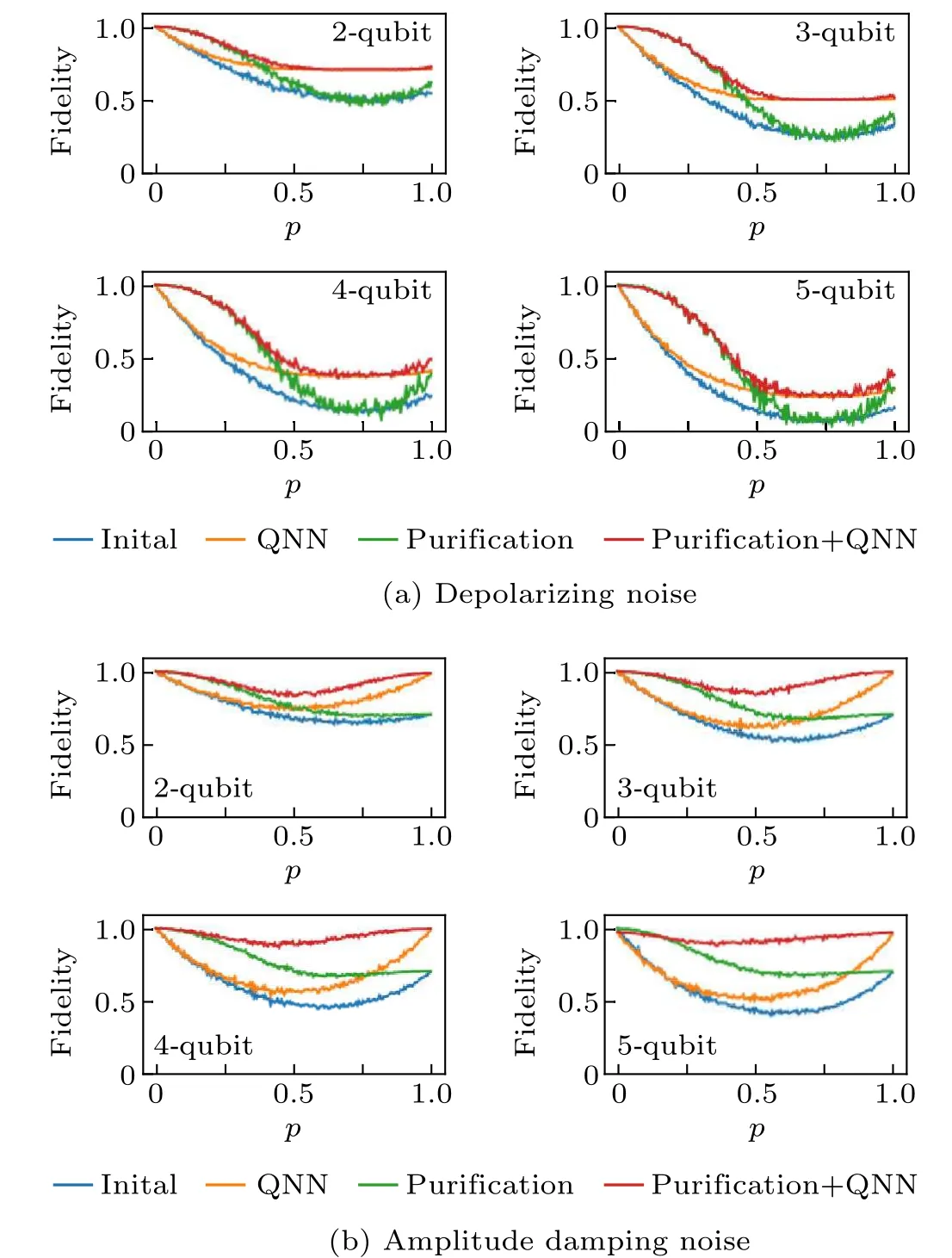
Fig.4. Fidelity of entanglement distribution. Here give four different dimensions in simulation under depolarizing and amplitude damping noise. p is the error probability of the channel noise.

To clarify the impact of dimension on entanglement distribution, we list the output of mixed scheme in Fig. 5. In the effective domain of purification,fidelity keeps in a similar high level for different dimension. In the effective domain of QNN, an interesting phenomenon appears. With the increasingp, fidelity decreases under depolarization noise, but under amplitude damping noise it decreases at the beginning and subsequently increases. And when the noise parameterpis close to 1, the rising fidelity almost can reach the ideal value of 1 under amplitude damping noise. Fidelity decreases under depolarizing noise and increases under amplitude damping noise with the increasing ofn. It is recognized that highdimensional entangled states have higher robustness towards noise. But it also brings extra noise because of more qubits.That is why the fidelity without purification or QNN decreases with the increasing ofn. However,combining purification and QNN can surely eliminate this additional noise under amplitude damping noise. Fortunately,amplitude damping noise is always considered to be the true channel noise for communication.

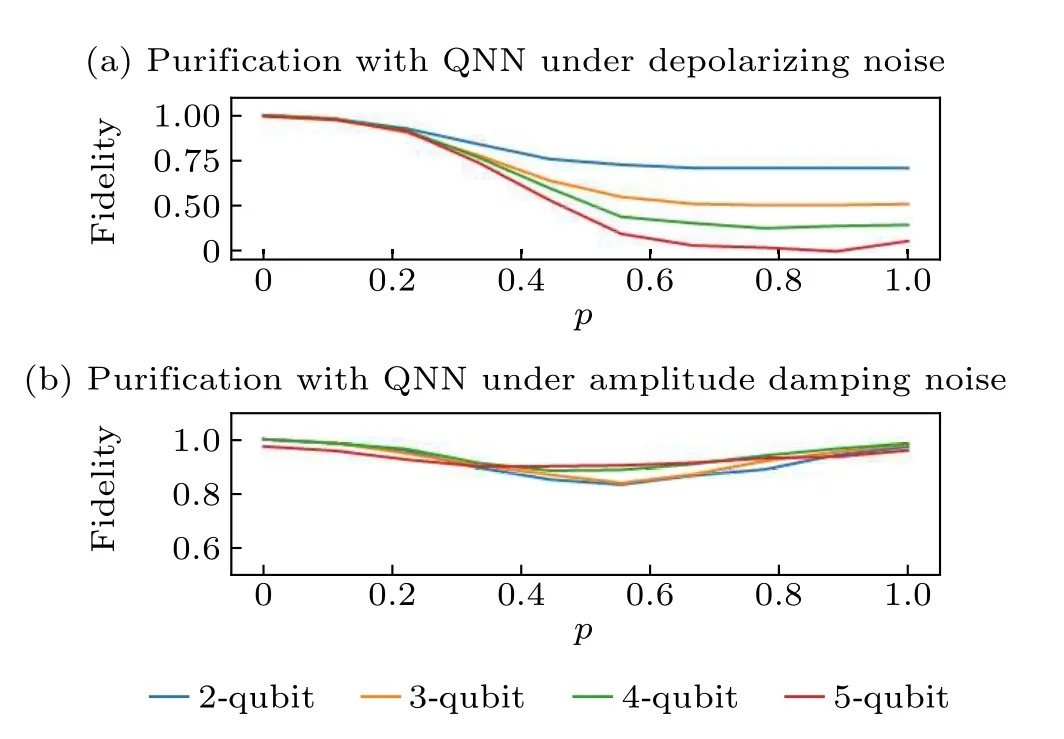
Fig. 5. Fidelity of different dimensions. The mixed scheme consists of purification and QNN.

We should point out that whenn ≥5,gradient explosion often occurs in the QNN under rotation mode. Besides, the cost function easily converges at 0.5. Both of them can lead to a failure in the QNN network training under amplitude damping noise. Instead of bringing improvement in fidelity, this failure leads to a significant reduction. With the increasing dimensionn,the training time will also increase,which is shown in Table 1 as well as the final cost value.

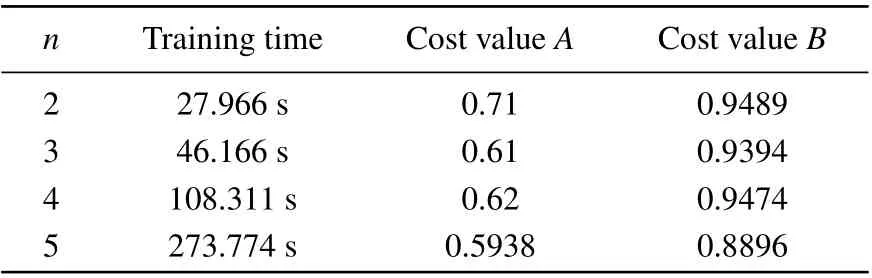
Table 1. Training time and cost value in QNN.

Whenn= 5, cost function under amplitude damping noise cannot always converge stably and keep at a high level.Thus,the fidelity of 5-qubit state decreases in the effective domain of purification. The cost in the QNN training is shown in Fig. 6. Convergence value of the cost under depolarizing noise is lower than that under amplitude damping noise. With the increasingn, convergence rate becomes slower. The fidelity under depolarization noise can rarely reach 0.8, while the fidelity under amplitude damping noise can exceed 0.9 in a wide range. Thus, our mixed scheme is more effective to non-unitary noise than unitary noise.

Combining purification and QNN expands the range of domain with high fidelity,especially towards amplitude damping noise. It can even reduce the influence of extra noise brought by dimension. Besides,the use of QNN does not consume extra entangled states. The network has been trained before entanglement distribution. Thus,only purification consumes qubits during the distribution. The team of D¨ur works a lot on the fidelity improvement of purification. But adjusting purification strategy in Ref.[12]cannot get higher fidelity under amplitude damping noise. The available domain with high fidelity is also small. Purification in Refs. [13,14] uses entangled states with higher dimension to purify states we want. The distribution of entanglement with high dimension is a thorny issue, which also leads to the waste of entangled states. Our scheme shows better comprehensive performance.

In brief, applying QNN on purification is a good choice for entanglement distribution. It improves the fidelity in a larger scale without consuming more entangled states. It also maximizes the fidelity gain brought by high dimension under non-unitary noise. Thus, it gives hope to the commercial application of quantum communication.

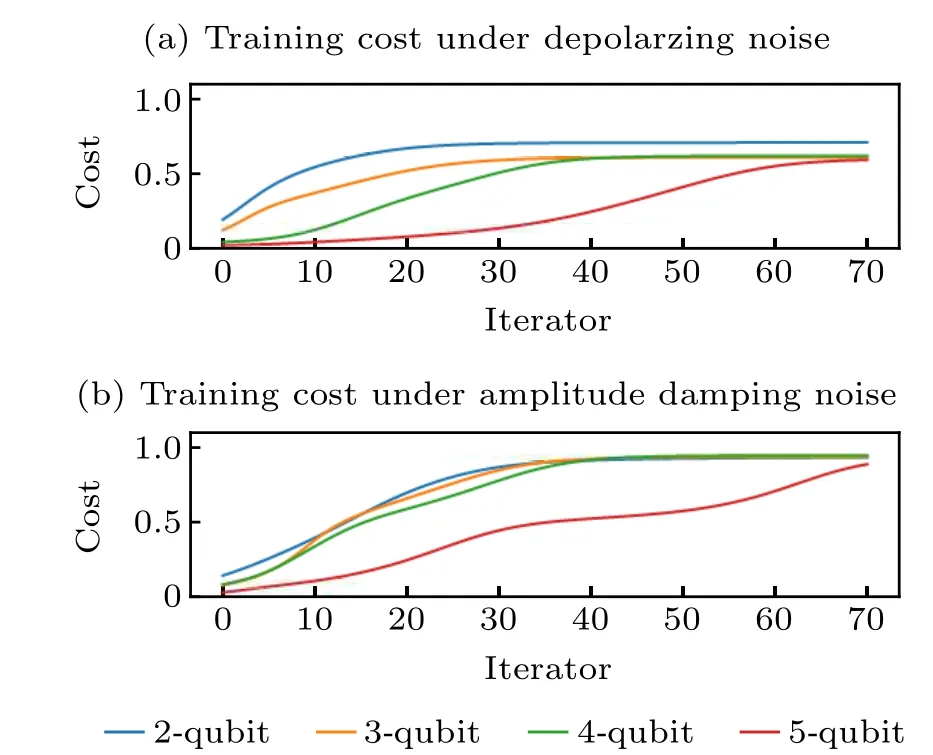
Fig.6. Cost function of training QNN under different noises.

5. Conclusion

In this paper, we have calculated the theoretical purification results under different noises and verify them on Cirq.Different from the previous purification protocol through adjusting quantum circuit, we introduced the use of QNN after purification. Clearly,combining purification and QNN can bring higher fidelity in the whole domain of error probability. It has better performance under amplitude damping noise,and brings additive fidelity gain with increasing dimension in the effective domain of QNN. It also brings an improvement in performance under depolarizing noise,but not so obvious. However, amplitude damping noise is always treated as the true channel noise in communication. Besides,the use of QNN during entanglement distribution does not consume extra entangled states. Thus, the mixed scheme we proposed has a good application prospect in entanglement distribution because of the high performance and low consumption.

There are still many issues need to be solved.Firstly,with the increasing number of input dimension,gradient explosion easily occurs in the network training. This can lead to the extremely low fidelity in the whole domain, even worse than the state without purification. Secondly, the simulation result under depolarizing noise appears not so ideal. Maybe there is some way to adjust the architecture of QNN to improve results higher under unitary noise.