王淑一, 孟凡偉

(曲阜師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,273165,山東省曲阜市)

0 引 言

2019年,Zada[1]證明了下列高階時(shí)滯微分方程的 Ulam 穩(wěn)定性

(1)

1990年,Meng[3]證明了下列高階方程解的漸近性

Lnu+g(s,u)=r(s),

受以上啟發(fā),我們利用自共軛微分算子研究高階時(shí)滯微分方程的 Ulam 穩(wěn)定性.

考慮自共軛微分算子形式下的高階微分方程

(2)

當(dāng)wj(s)=1,j=1,…,n時(shí),此時(shí)即是文獻(xiàn)[1]中的方程.

本文的主要目的是利用自共軛微分算子得到高階時(shí)滯微分方程 (2) 的 Ulam 穩(wěn)定性,推廣了文獻(xiàn)[1]中的結(jié)果.

1 預(yù)備知識(shí)及引理

令J1=[s0-ζ,s0+η],J2=[s0,s0+η],J3=[s0-ζ,s0],C(J1,) 表示從J1到的連續(xù)函數(shù)全體構(gòu)成的巴拿赫空間,且其范數(shù)為

根據(jù)文獻(xiàn)[3]中的結(jié)果,我們給出方程 (2) 的形式解.

定義1.1 若u(s) 是下列方程的解

則u(s) 滿足

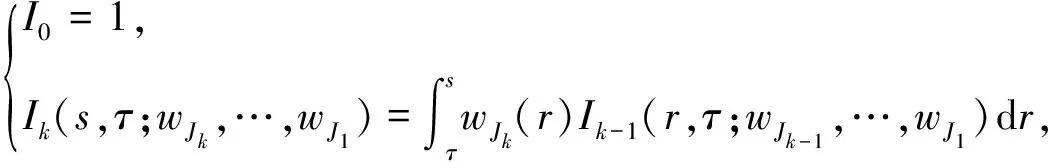
定義1.2 若v(s) 是下列微分不等式的解

其中θ>0,且存在 (2) 的解u(s) 和常數(shù)K>0 使得 |u(s)-v(s)|≤K·θ,s∈J1,則方程 (2) 具有 Hyers-Ulam 穩(wěn)定性.

定義1.3 若v(s) 是下列微分不等式的解

其中σ(s)≥0,且存在 (2) 的解u(s) 和常數(shù)Kg,σ>0 使得 |u(s)-v(s)|≤Kg,σ·σ(s),?s∈J1,則方程 (2) 具有 Hyers-Ulam-Rassias 穩(wěn)定性.

引理1.4[1]設(shè) (Y,d) 是度量空間,算子ψ:Y→Y.若?n∈,使得ψn在Y上是嚴(yán)格壓縮算子,則ψn和ψ在Y上具有相同的不動(dòng)點(diǎn).

引理1.5(Gronwall 引理) 令u(s),b(s)∈C([a,+∞],[0,+∞)),T≥0 是常數(shù).若u(s) 滿足

引理1.7[2]假設(shè)w(s),d(s),l(s),m(s),n(s) 是 [0,+∞) 到 [0,+∞) 上的連續(xù)函數(shù).若d(s) 和l(s) 在 [0,+∞)上是不減函數(shù),且w(s) 滿足

以及初始條件

w(s)=r(s),s∈[β,0],

其中

2 主要結(jié)果

在陳述主要定理之前,我們給出下列假設(shè).

(S1):

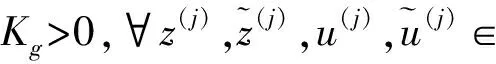
(S2):

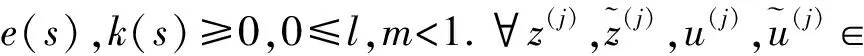
(S3):

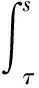
接下來(lái),給出方程 (2) 解的存在唯一性定理.

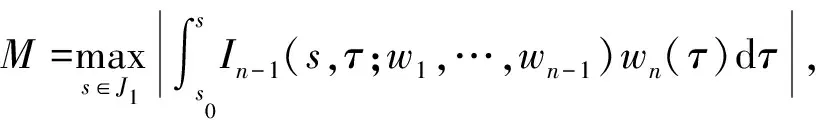
證明(ⅰ) 定義算子 Λ 如下:

首先證明 ?m∈+,使得 Λm是壓縮映射.令u1,u2∈C(J1,)∩Cn(J2,).

當(dāng)s∈J3時(shí),|(Λu1)(s)-(Λu2)(s)|=0,則 |(Λmu1)(s)-(Λmu2)(s)|=0.

當(dāng)s∈J2時(shí),

|(Λu1)(s)-(Λu2)(s)|=

g(τ,L0u2,…,Ln-1u2,L0u2(λ),…,Ln-1u2(λ))]dτ|≤

因此,可得 |(Λu1)(s)-(Λu2)(s)|≤2nKgM‖u1-u2‖.通過(guò)簡(jiǎn)單計(jì)算,可得|(Λmu1)(s)-(Λmu2)(s)|

≤(2nKgM)m‖u1-u2‖.根據(jù)定理?xiàng)l件,(2nKgM)m<1,則 Λm是壓縮映射.由引理 1.4 知,Λ 有唯一不動(dòng)點(diǎn)u,即方程 (2) 的唯一解.

(ⅱ)由定理?xiàng)l件知u(s)∈C(J1,)∩Cn(J2,) 是下列方程的解

因此,可得

若v(s) 滿足

那么

…,Ln-1v(λ))dτ|≤ηnθ.

當(dāng)s∈J3時(shí),|v(s)-u(s)|=0.

當(dāng)s∈J2時(shí),

g(τ,L0u,…,Ln-1u,L0u(λ),…,Ln-1u(λ))dτ|≤

對(duì)于上式,我們考慮算子A:C(J1,[0,+∞))→C(J1,[0,+∞)),定義如下

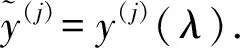
首先證明A是壓縮映射.

當(dāng)s∈J2時(shí),

|(Ay(j))(s)-(Ax(j))(s)|≤

因?yàn)?2nKgM<1,則A是壓縮映射.由壓縮映射原理,算子A是 Picard 算子,FA={ω(j)},則

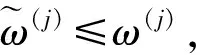
由 Gronwall-Bellman 不等式,可得

因?yàn)?|v(s)-u(s)|≤Ay(j)(s),則 |v(s)-u(s)|≤Aw(j)(s)=w(j)(s)≤Kε,即方程 (2) 具有 Hyers-Ulam 穩(wěn)定性.

定理2.2 假設(shè) (S2) 和 (S3) 成立.若v(s)∈C(J1,)∩Cn(J2,) 滿足

則存在方程 (2) 的解u(s) 滿足 |v(s)-u(s)|≤Kg,σ·σ(s),即方程 (2) 具有 Hyers-Ulam-Rassias 穩(wěn)定性,其中

V1(s)=lHlIn-1(s,τ;w1,…,wn-1)wn(s)e(s)+mHmIn-1(s,τ;w1,…,wn-1)wn(s)k(s).

證明因?yàn)閡(s) 是方程 (2) 的解,所以

由v(s) 所滿足的條件以及 (S3),可以簡(jiǎn)單計(jì)算出

當(dāng)s∈J3時(shí),|v(s)-u(s)|≤σ(s).

當(dāng)s∈J2時(shí),

g(τ,L0u,…,Ln-1u,L0u(λ),…,Ln-1u(λ))dτ|≤

g(τ,L0u,…,Ln-1u,L0u(λ),…,Ln-1u(λ))dτ|≤

[e(τ)|L0v-L0u|l+k(τ)|L0v(λ)-L0u(λ)|m]dτ|.

因此

因此

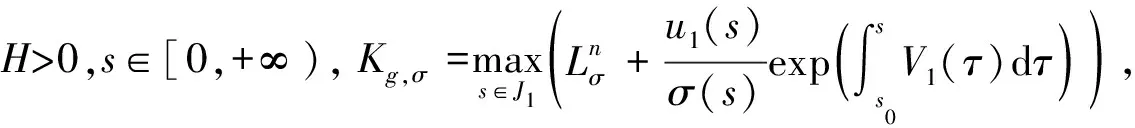
V1(s)=lHlIn-1(s,τ;w1,…,wn-1)wn(s)e(s)+mHmIn-1(s,τ;w1,…,wn-1)wn(s)k(s).

因此方程 (2) 具有 Hyers-Ulam-Rassias 穩(wěn)定性.

定理2.3 假設(shè) (S2) 成立,且v(s) 滿足

則存在方程 (2) 的解u(s) 滿足 |v(s)-u(s)|≤K·θ,即方程 (2) 具有 Hyers-Ulam 穩(wěn)定性,其中

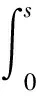
In-1(s,τ;w1,…,wn-1)wn(τ)k(τ)((1-m)Hm+mH1-mθηn)]dτ,

V1(s)=lHlIn-1(s,τ;w1,…,wn-1)wn(s)e(s)+mHmIn-1(s,τ;w1,…,wn-1)wn(s)k(s).

證明根據(jù)定理 2.2 的證明可得,當(dāng)s∈J3時(shí),|v(s)-u(s)|≤θ.

當(dāng)s∈J2時(shí),|v(s)-u(s)| ≤

根據(jù)引理1.7,令h=1,a=l,b=m,w(s)=|v(s)-u(s)|,d(s)=θηn,m(τ)=In-1(s,τ;w1,…,wn-1)wn(τ)e(τ),n(τ)=In-1(s,τ;w1,…,wn-1)wn(τ)k(τ),σ(τ)=λ(τ),l(s)=1,得

因此

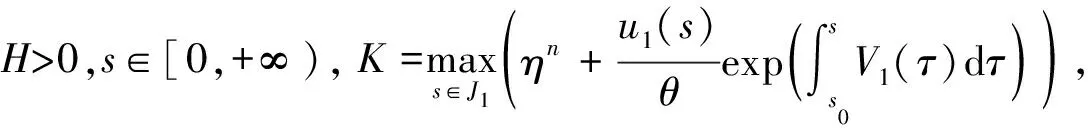
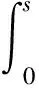
In-1(s,τ;w1,…,wn-1)wn(τ)k(τ)((1-m)Hm+mH1-mθηn)]dτ,

V1(s)=lHlIn-1(s,τ;w1,…,wn-1)wn(s)e(s)+mHmIn-1(s,τ;w1,…,wn-1)wn(s)k(s).

因此方程 (2) 具有 Hyers-Ulam 穩(wěn)定性.