許佳玲 賈利云? 劉超 吳佺 趙領(lǐng)軍 馬麗 侯登錄

1) (河北建筑工程學(xué)院數(shù)理系, 張家口 075000)

2) (河北師范大學(xué)物理學(xué)院, 石家莊 050016)

1 引 言

拓撲絕緣體HgTe 的發(fā)現(xiàn)引發(fā)了世界的轟動,尤其是最近我國在拓撲絕緣體領(lǐng)域取得了重大發(fā)現(xiàn), 預(yù)測了上千種可能的新型拓撲絕緣體材料, 這就使得對這一領(lǐng)域的研究方向由材料的探索轉(zhuǎn)變?yōu)椴牧闲再|(zhì)的研究[1,2].半Heusler 化合物與閃鋅礦結(jié)構(gòu)的相似性注定了其非凡的使命, 大量的研究致力于在Heusler 材料家族中尋找非平庸拓撲絕緣體材料[3?5].具有18 個電子的三元半Heusler 合金可以通過合適的應(yīng)力作用打開帶隙, 由此開啟了一個三維拓撲絕緣體的新系列[6?8].由于第一原理計算已證實此結(jié)構(gòu)體系拓撲Z2不變量沒有反對稱性的量子本質(zhì), 加上這個系列材料如磁性和超導(dǎo)性等其他有趣的物理性質(zhì), 于是基于密度泛函理論的第一性原理計算方法將三元半Heusler 化合物轉(zhuǎn)變?yōu)槿S拓撲絕緣體成為研究熱點[9,10].對于三維拓撲絕緣體半Heusler 化合物的研究, 結(jié)合這些材料的磁性和超導(dǎo)性質(zhì), 在實驗方面也成為了一個有巨大價值的研究平臺[11,12].

目前通過第一原理計算, 大量的半Heusler 三元化合物已經(jīng)被發(fā)現(xiàn)具有反帶結(jié)構(gòu), 例如LuPtSb,ScPtBi, YPdBi, ThPtPb, 都可以通過單軸應(yīng)力成為三維拓撲絕緣體的備選材料[13].通常, 對于具有小帶隙的半Heusler 化合物, 可以通過施加靜壓應(yīng)力改變帶序, 以及利用單軸應(yīng)力打開能隙的綜合方法實現(xiàn)拓撲絕緣體相[3].姚裕貴研究組[10]發(fā)現(xiàn):LaPtBi 在單軸應(yīng)力下可以實現(xiàn)拓撲絕緣體相, 未形變的的LaPtBi 的電子結(jié)構(gòu)作為原型系統(tǒng)顯示出明顯的能帶翻轉(zhuǎn)特征.通過施加[001]方向的單軸應(yīng)變可以實現(xiàn)三維拓撲絕緣體, 在保留翻轉(zhuǎn)帶序的同時可以打開帶隙, 并且通過計算不具有反對稱性的系統(tǒng)中的拓撲不變量Z2證明LaPtBi 是三維拓撲絕緣體.張小明等[14]又模擬了LaPtBi 在等體積下施加不同單軸拉壓應(yīng)力來破壞立方對稱性, 并實現(xiàn)了能帶的調(diào)控, 還對未形變體積下的單軸應(yīng)力也進行了詳細的研究.關(guān)于半Heusler 型化合物的能帶翻轉(zhuǎn)機制在參考文獻[15]中有較為詳細的論述,而且給出了一些設(shè)計的規(guī)則, 另外文中將HgTe 一類反轉(zhuǎn)帶序稱為β 型填充四面體結(jié)構(gòu)的拓撲半金屬, 這一類結(jié)構(gòu)已經(jīng)有人進行了大量的理論和實驗研究; 還有具有另一類反轉(zhuǎn)帶序的Heusler 體系拓撲絕緣體被稱為α 型填充四面體結(jié)構(gòu), 此類結(jié)構(gòu)的材料預(yù)測目前研究較少, 實驗研究幾乎還沒有開展.

Heusler 化合物研究始于由4 個面心立方子晶格組成的L21結(jié)構(gòu), 基于相似的面心晶格, 4 個Wyckoff 坐標分別為4a (0, 0, 0), 4b (1/2, 1/2, 1/2),4c (1/4, 1/4, 1/4) 和4d (3/4, 3/4, 3/4).4 個子晶格之中有一個沒有被填充, 就是C1b結(jié)構(gòu), 這種結(jié)構(gòu)通常也稱為半Heusler 結(jié)構(gòu).半Heusler 化合物的化學(xué)式一般寫為XYZ, 空間群為216如果用A, B, C 和D 表示4 個坐標位置, 可以把4 個面心立方子晶格看成4 個等效晶位, 用晶胞對角線連接起來, 半Heusler 結(jié)構(gòu)C 位沒有填充.由于目前的Heusler 化合物的組合方法一般是X 和Y 元素屬于在化學(xué)元素周期表中的過渡金屬元素,但是, 隨著材料模擬領(lǐng)域的發(fā)展以及實驗技術(shù)的進步, 其他元素如堿金屬等也被用于Heusler 化合物的研究.于是這就大大的擴展了Heusler 化合物的種類, 也極大地增大了各種Heusler 化合物的研究潛能.2015 年林詩源等[16]采用贗勢高通量方法計算了2295 種半Heusler 化合物, 并統(tǒng)計了 779 種拓撲絕緣體材料的能帶反轉(zhuǎn)強度和體結(jié)構(gòu)帶隙, 發(fā)現(xiàn)LiAuS 和 NaAuS 體系是非常優(yōu)異的拓撲絕緣體材料, 本部分工作主要參考采用贗勢的VASP軟件高通量計算結(jié)果, 根據(jù)擴展的元素種類用全勢方法研究α 型填充四面體結(jié)構(gòu)的拓撲絕緣體材料,計算Li(Na)AuS 體系拓撲絕緣體材料的能帶結(jié)構(gòu),由于Heusler 化合物研究很少有人利用S 放在主族元素所占的Z 位置上, 用S 作為主族元素, 采用貴金屬Au 占據(jù)A 位, 為保證18 個價電子, X 元素用比較活潑的堿金屬進行替代, 研究此類拓撲絕緣體的特點, 對拓撲絕緣體的理論和實驗研究具有參考價值.

2 計算方法

本工作中能帶結(jié)構(gòu)的計算是利用全勢線性綴加平面波方法的WIEN2k 來進行的.交換關(guān)聯(lián)泛函主要是采用了傳統(tǒng)的局域自旋密度近似(LSDA)和修正的Becke-Johnson 交換勢 (MBJ).在計算中均對重金屬元素考慮了自旋軌道耦合的效果.軟件利用四面體網(wǎng)格法對于波矢進行積分, 選取5000 個k 點.截斷參數(shù)選取Rmt× Kmax= 9.為了驗證計算結(jié)果的可靠性, 采用LSDA 和MBJ 驗算了拓撲絕緣體材料LiAuS 的能帶結(jié)構(gòu), 對比文獻中的采用廣義梯度近似(GGA)和雜化泛函(HSE)的計算結(jié)果.

3 結(jié)果和討論

3.1 不同關(guān)聯(lián)泛函LiAuS 能帶結(jié)構(gòu)

通過計算發(fā)現(xiàn)LiAuS 和NaAuS 具有反帶結(jié)構(gòu), 這個結(jié)論和文獻[15]中采用GW 近似方法得到的結(jié)果一致; 另外, 對于反帶結(jié)構(gòu)和反轉(zhuǎn)強度的討論, 文獻[16]中進行了細致的討論, 不再作為本文討論的重點.利用GGA, LSDA 和MBJ 三種關(guān)聯(lián)泛函計算了LiAuS.各個化合物的平衡晶格常數(shù)都是通過能量優(yōu)化得到的.通過比較能量優(yōu)化得到的晶格常數(shù), 發(fā)現(xiàn)采用全勢GGA 泛函得到的平衡晶格常數(shù)為0.602 nm, 稍大于VASP 贗勢軟件GGA計算值的0.599 nm, 而采用LSDA 泛函優(yōu)化得到的平衡晶格常數(shù)為0.586 nm, 可見局域密度泛函得到的平衡晶格常數(shù)為最小.通過各自平衡晶格常數(shù)計算得到的能帶圖結(jié)構(gòu)均為具有反帶結(jié)構(gòu)的拓撲絕緣體結(jié)構(gòu), 且均打開了自然帶隙, 結(jié)果和文獻一致, 但是在帶隙數(shù)值上MBJ 并沒有顯現(xiàn)出優(yōu)勢.對于LaPtBi 材料一般在平衡狀態(tài)為反帶結(jié)構(gòu), 但是并沒有帶隙, 普遍認為具有此類反帶結(jié)構(gòu)的立方半Heusler 化合物要想打開體能隙, 常用的方法就是施加等體積單軸應(yīng)力, 施加拉應(yīng)力可以增大帶隙, 從而得到真正意義上的拓撲絕緣體材料, 這種方法的實質(zhì)是通過破壞立方對稱性的保護而打開帶隙[17,18].圖1 表示對LiAuS 在保證體積不變的基礎(chǔ)上對c 軸施加單軸應(yīng)力得到的能量優(yōu)化曲線,由于施加拉應(yīng)力可以增大帶隙, 所以應(yīng)力施加是以拉應(yīng)力為主, 圖中橫坐標的–10 表示施加10%的單軸壓應(yīng)力, 而橫坐標的正值均表示拉應(yīng)力.由圖中可知, 當單軸拉力施加到約41%處能量最低, 此時破壞了立方對稱性之后成為四方結(jié)構(gòu)后空間群為且平衡晶格常數(shù)為a = 0.52477 nm,c/a = 1.41 時系統(tǒng)又趨于平衡狀態(tài).

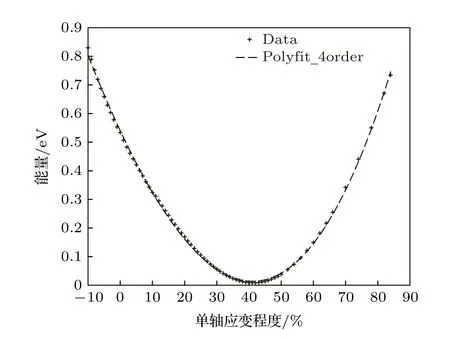
圖1 對LiAuS 在保證體積不變的基礎(chǔ)上對c 軸施加單軸應(yīng)力得到的能量優(yōu)化曲線, c/a = 1.41 時得到平衡晶格常數(shù)為a = 0.52477 nmFig.1.Calculated total energies as functions of the uniaxial strain along [001] direction with constant volume for LiAuS,the equilibrium lattice constant is a = 0.52477 nm and c/a= 1.41.

研究認為有必要對堿金屬系列半Heusler 化合物的拓撲絕緣體進行計算和分析, 另外由于全勢的WIEN2k 軟件包的MBJ 是原生的, 因此采用LSDA 和MBJ 兩種關(guān)聯(lián)泛函計算此系列的能帶進行比較.圖2 給出了利用WIEN2k 軟件分別采用LSDA 和MBJ 兩種關(guān)聯(lián)泛函計算得到的對LiAuS施加1%的單軸拉力得到的能帶結(jié)構(gòu)圖, 可以發(fā)現(xiàn)較小的單軸應(yīng)力破壞立方結(jié)構(gòu)后也破壞了此類拓撲絕緣體的自然帶隙, 通過計算得到施加較小的拉力和壓力均會使系統(tǒng)由拓撲絕緣體轉(zhuǎn)變?yōu)橥負浣饘?

圖3 給出了單軸應(yīng)力下平衡狀態(tài)下采用LSDA和MBJ 兩種關(guān)聯(lián)泛函計算得到的LiAuS 的能帶結(jié)構(gòu)圖.從圖3 可以看出, 通過施加單軸拉應(yīng)力直到四方結(jié)構(gòu)的平衡位置時, 系統(tǒng)帶隙的值為0.2 eV 左右, 這與立方結(jié)構(gòu)平衡位置得到的帶隙結(jié)果一致.一般情況下, 計算半導(dǎo)體和絕緣體材料,利用GGA 方法計算得到的能帶帶隙要比MBJ 的要小, 也就是通常所說的GGA 會低估帶隙, 發(fā)現(xiàn)在此系列的拓撲絕緣體帶隙計算中, 每種關(guān)聯(lián)泛函得到的帶隙是一致的, 所以證實這是材料本身的屬性.但是, 在結(jié)果中通過MBJ 泛函計算得到的能帶圖中, 費米能級明顯穿過了價帶.通過計算發(fā)現(xiàn),在此體系的半Heusler 化合物中, MBJ 泛函在拓撲絕緣體的計算中并沒有明顯優(yōu)勢.而在LSDA計算得到的能帶圖中, 在拉力作用下, Au 的部分s 軌道明顯能量下降, 在局域密度近似當中尤其明顯, 拉力為84%嚴重破壞立方對稱性時, 帶隙值仍然約為0.2 eV.

3.2 Li(Na)AuS 體系的化學(xué)替代

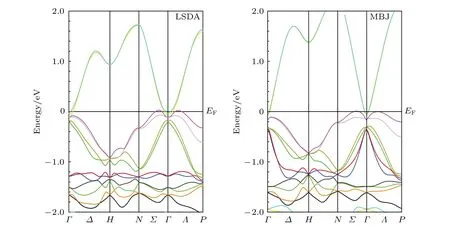
圖2 施加1%拉應(yīng)力后破壞立方結(jié)構(gòu)的能帶結(jié)構(gòu), 左圖為LSDA 計算能帶圖, 右圖為MBJ 計算得到的能帶圖Fig.2.Band structure of the LiAuS compound with 1% uniaxial tensile stress, on the left with LSDA, and on the right with MBJ.

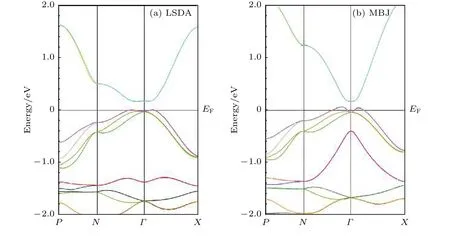
圖3 四方結(jié)構(gòu)平衡晶格常數(shù)(a = 0.52477 nm, c/a = 1.41)下的能帶結(jié)構(gòu) (a) LSDA 計算能帶圖; (b) MBJ 計算得到的能帶圖Fig.3.Band structure of the tetragonal structure LiAuS compound with the equilibrium lattice constant (a = 0.52477 nm and c/a =1.41): (a) LSDA; (b) MBJ.

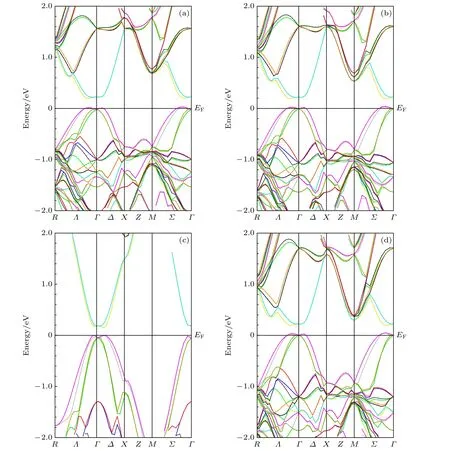
圖4 摻雜結(jié)構(gòu)在各自平衡晶格常數(shù)下的能帶結(jié)構(gòu) (a) Li0.125Na0.875AuS; (b) Li0.375Na0.625AuS; (c) Li0.5Na0.5AuS; (d) Li0.875Na0.125AuSFig.4.Band structure of the LixNa1 – xAuS compound with the equilibrium lattice constant: (a) Li0.125Na0.875AuS; (b) Li0.375 Na0.625AuS; (c) Li0.5Na0.5AuS; (d) Li0.875Na0.125AuS.

從前面的計算中可以看出, 等體積的單軸拉應(yīng)力作用下破壞了立方對稱性從而打開了拓撲絕緣體的能隙, 但是在實際材料的制備過程中, 等體積的單軸拉應(yīng)力的實現(xiàn)存在困難.對于Heusler 化合物體系, 在實驗上通過對某個原子同族的元素替換進行摻雜是比較常用的手段, 在保證價電子濃度不變的前提下, 通過摻雜可以改變晶格常數(shù)、電負性,甚至實現(xiàn)半金屬性, 還可以找到具有相變的新材料[19].實驗上采用化學(xué)摻雜在Heusler 化合物中獲得成功的例子數(shù)不勝數(shù), 由于化學(xué)摻雜也是對體系立方對稱性的破壞, 因此運用同族元素替代的手段, 期望在保證材料拓撲絕緣體性質(zhì)的同時, 不改變立方結(jié)構(gòu), 在體系的平衡晶格常數(shù)下使得材料的帶隙打開, 從而提高實驗合成拓撲絕緣體材料的可行性[20?22].

選取上文論述中兩種本身都具有反帶結(jié)構(gòu)的材料, 觀察Li 和Na 相互取代過程中是否能夠打開帶隙, 依次采用LSDA 計算了相互替代比例為12.5%, 25.0%, 37.5%, 50.0%, 62.5%, 75.0%和87.5%的超胞結(jié)構(gòu)的能帶.首先進行擴胞形成2 × 2 × 1超胞結(jié)構(gòu), 原子替換依據(jù)原有的套嵌結(jié)構(gòu)由外側(cè)立方頂角位置開始依次更換, 對于不同替代比例相應(yīng)的超胞結(jié)構(gòu)首先進行能量優(yōu)化獲得平衡晶格常數(shù),然后利用各自的平衡體積進行能帶計算, 并且考慮自旋軌道耦合, 其他計算參數(shù)與前面的計算一致.相互替代時沒有考慮無序狀態(tài), 只研究由于摻雜引起體系立方對稱性的破壞對能隙穩(wěn)定性的影響.如圖4 所示, 結(jié)果發(fā)現(xiàn)Li0.125Na0.875AuS,Li0.375Na0.625AuS, Li0.5Na0.5AuS, Li0.625Na0.375AuS,Li0.875Na0.125AuS 都可以在平衡位置打開能隙,而且在費米面位置處導(dǎo)帶底和價帶頂?shù)哪軒址€(wěn)定, 均為直接帶隙, 帶隙值約為0.2 eV 左右.進行替換后, 化合物材料的空間群由原來的216變?yōu)閷ΨQ性稍有下降; 而替換50%時生成結(jié)構(gòu)的空間群為立方對稱性遭到破壞的程度較為強烈, 不同比例下由于進行元素替代導(dǎo)致的對稱性變化引起了能帶圖沿著高對稱線能帶的簡并度的不同, 另外由于樣品對應(yīng)的平衡晶格常數(shù)不同, 也使能帶圖出現(xiàn)微小變化.本文得到的大量研究結(jié)果可以對半Heusler 合金結(jié)構(gòu)拓撲絕緣體的進一步理論研究和實驗研究提供依據(jù).

4 結(jié) 論

通過全勢線性綴加平面波方法計算Li(Na)AuS體系拓撲絕緣體材料的能帶結(jié)構(gòu), 通過比較能量優(yōu)化得到的晶格常數(shù), 發(fā)現(xiàn)采用全勢GGA 泛函得到的平衡晶格常數(shù)大于贗勢計算值, 局域自旋密度LSDA 泛函得到的平衡晶格常數(shù)為最小.通過各自平衡晶格常數(shù)計算得到的能帶圖結(jié)構(gòu)均為具有反帶結(jié)構(gòu)的拓撲絕緣體結(jié)構(gòu), 而且均打開了自然帶隙, 但是在帶隙數(shù)值上MBJ 并沒有顯現(xiàn)出優(yōu)勢.較小的單軸應(yīng)力破壞立方結(jié)構(gòu)后也破壞了此類拓撲絕緣體的自然帶隙, 通過施加單軸拉應(yīng)力直到四方結(jié)構(gòu)的平衡位置時, 系統(tǒng)帶隙值約為0.2 eV,這與立方結(jié)構(gòu)平衡位置得到的帶隙結(jié)果一致.由于化學(xué)摻雜也是對體系立方對稱性的破壞, 運用同族元素替代的手段, 實現(xiàn)了在保證材料拓撲絕緣體性質(zhì)的同時, 不改變立方結(jié)構(gòu), 在體系的平衡晶格常數(shù)下使得材料的帶隙打開.

感謝河北工業(yè)大學(xué)材料科學(xué)與工程學(xué)院張小明老師的指導(dǎo)和幫助.