一類(lèi)熱傳導(dǎo)系數(shù)跳躍的非Fourier溫度場(chǎng)分布的奇攝動(dòng)雙參數(shù)解
包立平,李文彥,吳立群
(1.杭州電子科技大學(xué)理學(xué)院,浙江杭州310018;2.杭州電子科技大學(xué)機(jī)械工程學(xué)院,浙江杭州310018)
§1 引 言
隨著超短脈沖激光加熱,金屬快速凝固等現(xiàn)代高新技術(shù)的發(fā)展,熱作用的周期時(shí)間短到皮秒以至飛秒量級(jí)的超急速,超常規(guī)熱傳導(dǎo)規(guī)律的研究越來(lái)越引起人們的重視.
在許多實(shí)際物理問(wèn)題中,會(huì)遇到含有間斷系數(shù)的擴(kuò)散問(wèn)題,例如,熱傳導(dǎo)過(guò)程中在不同溫度下,熱傳導(dǎo)系數(shù)會(huì)出現(xiàn)間斷[1],從而這些物理問(wèn)題的數(shù)學(xué)模型就歸結(jié)于間斷系數(shù)問(wèn)題.如何有效和準(zhǔn)確地求解它們?nèi)匀皇且粋€(gè)很大的挑戰(zhàn).雖然許多學(xué)者針對(duì)這類(lèi)問(wèn)題的數(shù)值求解作了大量的研究工作,但是使用經(jīng)典的有限元方法求解很難獲得高精度的數(shù)值解.關(guān)建飛,沈中華[1-2]等人用Fourier熱傳導(dǎo)定律描述了板狀金屬材料中脈沖激光激發(fā)的超聲波,并用有限元方法進(jìn)行了數(shù)值模擬.對(duì)于常規(guī)條件下的非穩(wěn)態(tài)熱傳導(dǎo)問(wèn)題,人們常常采用Fourier熱傳導(dǎo)定律來(lái)描述熱流密度與溫度梯度之間的關(guān)系,也足夠精確,但是延伸到溫度急劇變化的場(chǎng)合,用Fourier熱傳導(dǎo)定律來(lái)描述將存在問(wèn)題,因此使用非Fourier熱傳導(dǎo)定律更合適.李金娥[3]建立了一個(gè)雙層材料層合板瞬態(tài)加熱情況下的非Fourier熱傳導(dǎo)分析模型,用向后差分法得到了溫度場(chǎng)的數(shù)值解.張浙[4]對(duì)非Fourier熱傳導(dǎo)的性質(zhì),模型,模型的求解及應(yīng)用與實(shí)驗(yàn)等幾個(gè)方面的研究進(jìn)展做了一個(gè)較詳盡的概括與評(píng)述,并指出了今后需要著重研究的方向,采用非Fourier熱傳導(dǎo)定律來(lái)構(gòu)建模型,考慮由于溫度急劇變化熱傳導(dǎo)系數(shù)出現(xiàn)跳躍的情況,得到了非線性的具有間斷系數(shù)的奇攝動(dòng)雙曲方程.劉法貴,葛云飛,李才中[5]考慮具間斷系數(shù)線性雙曲型方程組Riemann問(wèn)題,利用分析的方法證明了該問(wèn)題包含波解的存在性.張志娟,蔚喜軍[6]討論了一維,二維具有間斷系數(shù)拋物方程的LDG方法,進(jìn)行了穩(wěn)定性分析,并給出了解的誤差估計(jì),但獲得該結(jié)果對(duì)真解的光滑性要求比較高.張榮培,蔚喜軍和崔霞應(yīng)[7]用間斷方法求解帶有間斷系數(shù)的二維橢圓方程針對(duì)擴(kuò)散系數(shù)間斷的特點(diǎn),構(gòu)造了一種新的加權(quán)對(duì)稱(chēng)內(nèi)懲罰方法證明了相應(yīng)雙線性形式的連續(xù)性和強(qiáng)制性,并給出收斂性證明數(shù)值算例表明該方法對(duì)于求解強(qiáng)間斷系數(shù)問(wèn)題是有效的.常洛[8]考慮了間斷系數(shù)拋物方程的顯隱格式區(qū)域分裂有限元方法,在子區(qū)域內(nèi)部應(yīng)用隱式方法,子區(qū)域相鄰內(nèi)邊界條件值由一個(gè)函數(shù)在前層的值給出,從而實(shí)現(xiàn)了并行計(jì)算.該方法在子區(qū)域內(nèi)部和跨越內(nèi)邊界時(shí)都保證了問(wèn)題的守恒性,經(jīng)過(guò)理論分析得到了誤差估計(jì)并給出了數(shù)值算例.Rauf Amirov[9]構(gòu)造了新的積分來(lái)表示具有分段常導(dǎo)系數(shù)和間斷條件的Sturm-Liouville方程的基本解,并且研究了邊值問(wèn)題的重要譜性質(zhì).上述文獻(xiàn)都是通過(guò)數(shù)值模擬的方法得到相關(guān)結(jié)果.
本文考慮脈沖激光作用于材料表面基于熱彈機(jī)制產(chǎn)生的溫度場(chǎng),過(guò)去通常用Fourier熱傳導(dǎo)定律描述由激光激發(fā)的溫度場(chǎng),但在瞬態(tài)熱傳導(dǎo)過(guò)程中(特別是某些極端情況,如激光加熱等),熱量傳遞具有和經(jīng)典熱傳導(dǎo)理論所認(rèn)為的擴(kuò)散行為完全不同的物理機(jī)制,物理機(jī)制的差異反映在描述物理行為的數(shù)學(xué)表達(dá)式上,就是說(shuō)以經(jīng)典的Fourier定律為基礎(chǔ)建立起來(lái)的熱傳導(dǎo)理論,已不能對(duì)這種情況下的熱量傳遞規(guī)律做出合理的解釋,因此采用非Fourier熱傳導(dǎo)定律構(gòu)造模型,克服了這一問(wèn)題.由于熱松弛時(shí)間特別小,因此可以將該問(wèn)題視為奇攝動(dòng)雙曲方程問(wèn)題.通過(guò)建立模型.應(yīng)用奇攝動(dòng)方法來(lái)求解.康連城[10]研究了一類(lèi)具有非線性初邊值條件的奇攝動(dòng)問(wèn)題的n維擬線性雙曲拋物型方程,給出了該攝動(dòng)問(wèn)題光滑解具有一致有效的一階漸近展開(kāi)式的存在性.文獻(xiàn)[11]研究了一類(lèi)具有變動(dòng)邊界的初邊值問(wèn)題的奇攝動(dòng)的擬線性雙曲拋物型方程,給出了此問(wèn)題的解具有以退化問(wèn)題充分光滑解為首項(xiàng)的廣義漸近展開(kāi)式的存在性.但文獻(xiàn)[10-11]的模型并未出現(xiàn)系數(shù)間斷的情況,宋明玲[12]研究了多維空間上具有間斷系數(shù)的半線性雙曲型方程柯西問(wèn)題局部解的存在性和唯一性,文獻(xiàn)[13]研究了一類(lèi)具有連續(xù)勢(shì)壘和不連續(xù)(左或右連續(xù))發(fā)生器的一維反射后向雙隨機(jī)微分方程,得到了該隨機(jī)微分方程解的存在性定理和比較定理.文獻(xiàn)[14]介紹了一類(lèi)非光滑系統(tǒng)的幾何理論,將理論引入到綜合數(shù)學(xué)中的幾何學(xué)與拓?fù)鋵W(xué)中.但只是研究了解的存在唯一性,并沒(méi)有確定位置關(guān)系,文獻(xiàn)[15]研究了一類(lèi)漂移和擴(kuò)散系數(shù)都可能不連續(xù)的一類(lèi)隨機(jī)微分方程的Euler-MuluyAMa逼近的強(qiáng)收斂性.文獻(xiàn)[16]研究了一類(lèi)非光滑的奇攝動(dòng)動(dòng)力系統(tǒng),在系數(shù)出現(xiàn)間斷時(shí),利用爆破技術(shù)對(duì)非光滑動(dòng)力系統(tǒng)進(jìn)行正則化.文獻(xiàn)[17]研究了具有間斷源項(xiàng)的半線性微分方程奇攝動(dòng)問(wèn)題,針對(duì)這些問(wèn)題,構(gòu)造了一個(gè)適當(dāng)?shù)姆侄尉鶆蚓W(wǎng)格的數(shù)值方法,該方法對(duì)于奇異攝動(dòng)參數(shù)是一致收斂的,數(shù)值結(jié)果驗(yàn)證了理論結(jié)果.文獻(xiàn)[1-2]提到了熱傳導(dǎo)系數(shù)出現(xiàn)間斷的情況,但只是用有限元方法數(shù)值模擬計(jì)算的.目前來(lái)說(shuō),尚未見(jiàn)到關(guān)于具有間斷系數(shù)的奇攝動(dòng)雙曲方程的研究的報(bào)導(dǎo),特別是間斷位置未定的情形未見(jiàn)研究結(jié)果.
本文用非Fourier熱傳導(dǎo)定律來(lái)描述脈沖激光作用于材料表面基于熱彈機(jī)制產(chǎn)生的溫度場(chǎng),考慮由于溫度急劇變化熱傳導(dǎo)系數(shù)出現(xiàn)跳躍的情況,得到了非線性的具有間斷系數(shù)的奇攝動(dòng)雙曲方程.應(yīng)用奇攝動(dòng)雙參數(shù)展開(kāi)法得到該問(wèn)題的展開(kāi)式,并且得到了內(nèi)外解的存在唯一性,進(jìn)而確定了熱傳導(dǎo)系數(shù)跳躍的位置關(guān)系.并用縫接法將熱傳導(dǎo)系數(shù)發(fā)生跳躍的位置兩邊的解縫接起來(lái),從而得到了解的形式漸近展開(kāi)式.其次通過(guò)余項(xiàng)估計(jì),得到了漸近解的一致有效性,從而得到了完整溫度場(chǎng)的分布,為非Fourier熱傳導(dǎo)在非均勻材料領(lǐng)域中的應(yīng)用研究提供參考依據(jù).
§2 模型建立
現(xiàn)在作如下的假設(shè):
[H1]φ(t),λ(x)是已知的任意階連續(xù)可微函數(shù),且φ(0)=0,φ0(t)≥0.
[H2]熱傳導(dǎo)系數(shù)
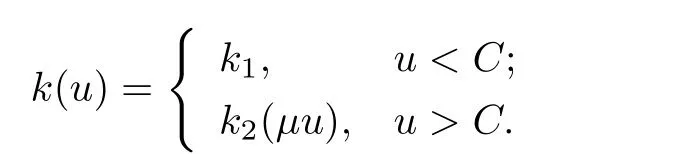
其中k1和C為正常數(shù),k2的導(dǎo)函數(shù)連續(xù),μ是小參數(shù).假設(shè)熱傳導(dǎo)系數(shù)在u=C處發(fā)生跳躍的位置為x=?(t,ε),t? x=?(t,ε)待定. 由文獻(xiàn)[4],可得非Fourier熱傳導(dǎo)的單相延遲熱傳導(dǎo)模型,考慮熱流矢量的傳播和溫度梯度的關(guān)系 其中ε為相位延遲,k(u)為熱傳導(dǎo)系數(shù).能量方程為 因此 所以 由文獻(xiàn)[1-2]可知,在多種材料中會(huì)出現(xiàn)熱傳導(dǎo)系數(shù)間斷的情形.因此本文討論的(1)中的熱傳導(dǎo)系數(shù)滿(mǎn)足假設(shè)[H1]的假定,即熱傳導(dǎo)系數(shù)跳躍的非Fourier溫度場(chǎng)問(wèn)題 初始條件和邊界條件分別為 由假設(shè)[H2],k(u)是不連續(xù)的,在u=C存在一跳躍間斷點(diǎn),且在u=C處,x=?(t,ε),t? 令?1={(x,t)∈[0,L]×[0,T]|u(x,t) 因此問(wèn)題(1)-(2)可改寫(xiě)為 其中?1的邊界??1={(x,t)|0≤t≤t?,x=L}∪{(x,t)|t=0,0≤x≤L}∪{(x,t)|0≤t≤t?,x=0}∪{(x,t)|t?≤t≤T,x=?(t,ε)},?2的邊界??2={(x,t)|t?≤t≤T,x=?(t,ε)}∪{(x,t)|t?≤t≤T,x=0}. 分別對(duì)(3),(4)構(gòu)造形式漸近解,首先給出(3)的合成展開(kāi)式 其中 將(6)代入到(3)中,比較ε的同次冪系數(shù),可得: 比較εμ的同次冪系數(shù),可得: 在有界域上,根據(jù)線性?huà)佄锓匠汤碚?可得到(7)-(10)和(15)-(16)的存在唯一性. 定理1(1)中的熱傳導(dǎo)系數(shù)k(u)在u=C處發(fā)生跳躍的位置為 證令δ為充分小的正常數(shù),kδ(u)∈C∞(R),滿(mǎn)足 現(xiàn)考慮問(wèn)題 邊界條件和初始條件為 令 則ω1t(x,t)=?φ0(t)+(kδ(u)ω1x)x,ω1(0,t)=0,ω1(x,0)=0,ω1(L,t)=?φ(t)≤0. 應(yīng)用De Giorgi迭代技術(shù),由極值原理可得ω1≤0. 因此uδ(x,t)≤φ(t).令ω2(x,t)=uδx(x,t),可得 本文采用非Fourier熱傳導(dǎo)定律來(lái)構(gòu)造溫度場(chǎng)模型,考慮由于溫度急劇變化導(dǎo)致熱傳導(dǎo)系數(shù)出現(xiàn)跳躍的情況,得到了非線性的具有間斷系數(shù)的奇攝動(dòng)雙曲方程.應(yīng)用奇攝動(dòng)雙參數(shù)展開(kāi)法得到該問(wèn)題的展開(kāi)式,并且得到了內(nèi)外解的存在唯一性,進(jìn)而確定了熱傳導(dǎo)系數(shù)出現(xiàn)跳躍的位置關(guān)系.并用縫接法將熱傳導(dǎo)系數(shù)發(fā)生跳躍的位置兩邊的解縫接起來(lái),從而得到了解的形式漸近展開(kāi)式.其次,通過(guò)余項(xiàng)估計(jì),得到了漸近解的一致有效性,從而得到了熱傳導(dǎo)系數(shù)跳躍的非Fourier溫度場(chǎng)的完整分布.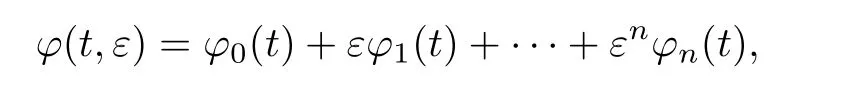
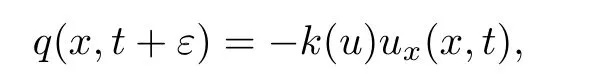
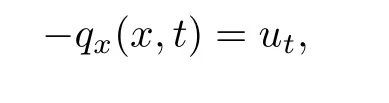
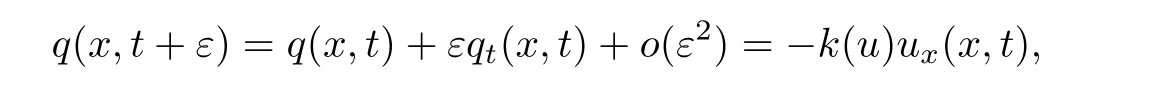
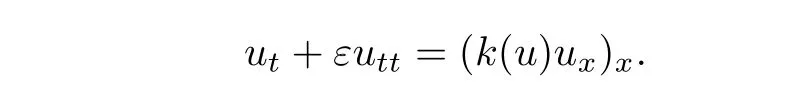
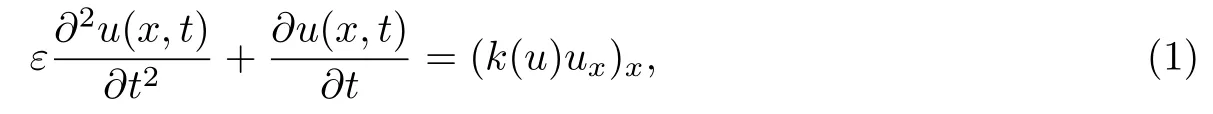
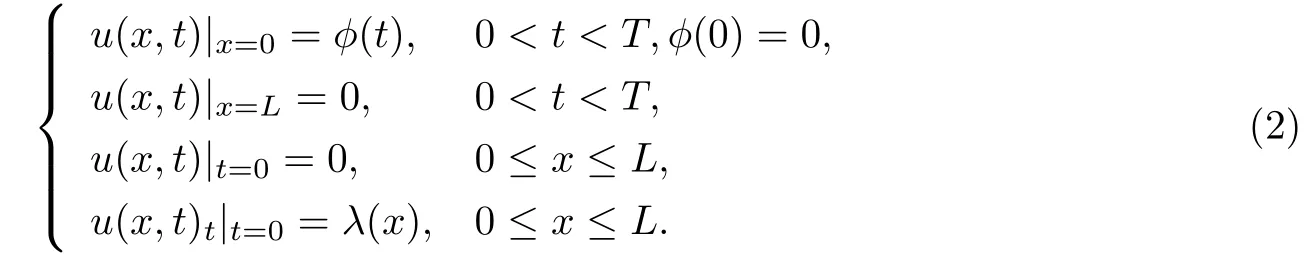
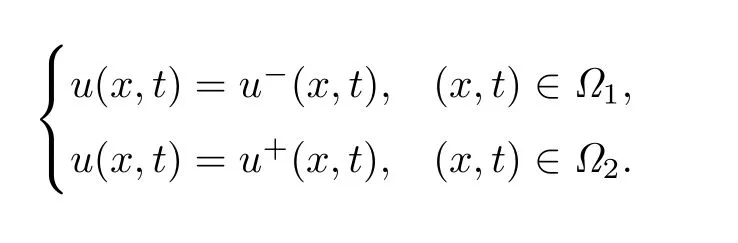
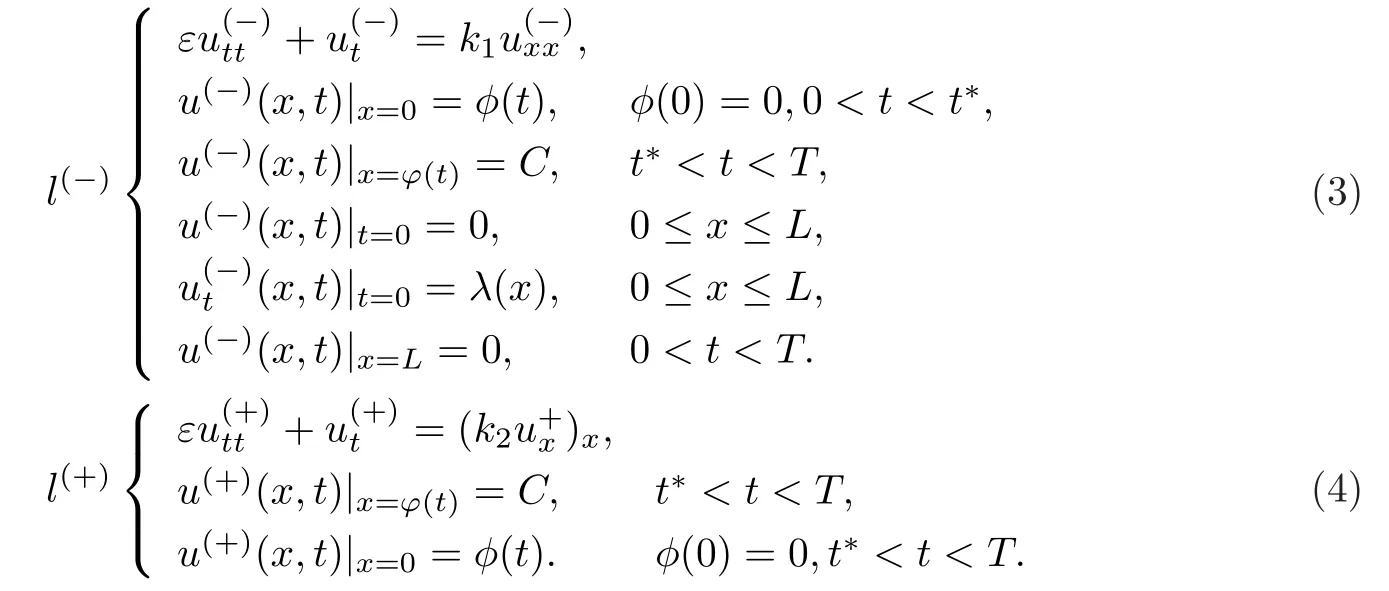
§3 形式展開(kāi)
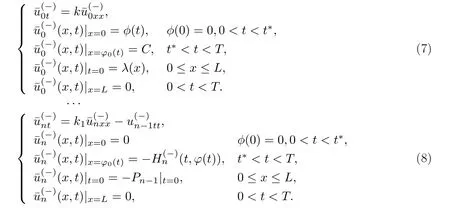


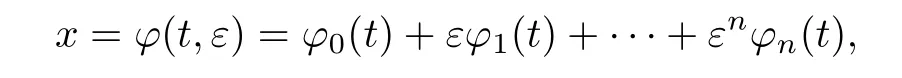
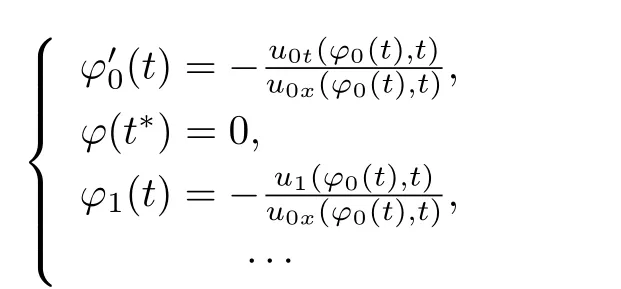
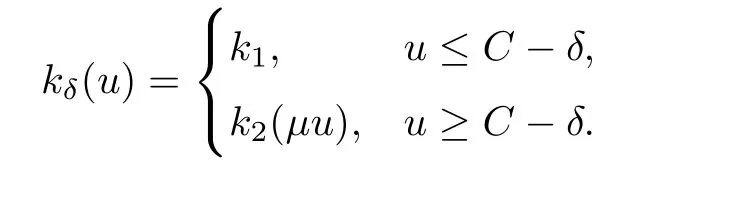

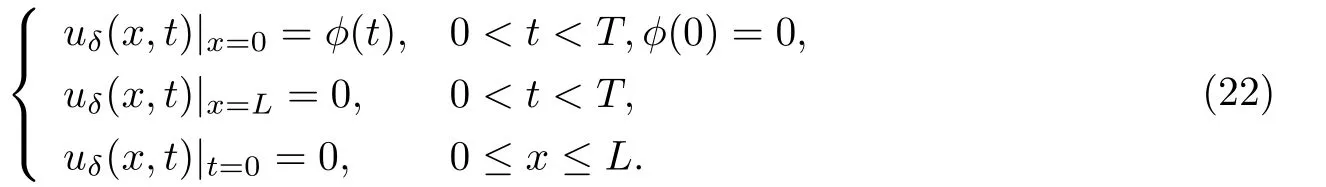
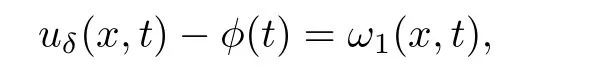


§4 余項(xiàng)估計(jì)



§5 結(jié)束語(yǔ)

