吳秀峰, 黃俊杰

(1.內(nèi)蒙古師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,內(nèi)蒙古呼和浩特010022;2.內(nèi)蒙古大學(xué)數(shù)學(xué)科學(xué)學(xué)院,內(nèi)蒙古呼和浩特010021)

§1 引 言

缺少了某些元素的算子矩陣稱為缺項(xiàng)算子矩陣.算子矩陣的譜補(bǔ)問(wèn)題旨在討論缺項(xiàng)算子矩陣中所缺的元素對(duì)整個(gè)算子矩陣譜的影響,在插值理論,換位提升理論,以及系統(tǒng)控制理論中具有重要應(yīng)用.缺項(xiàng)算子矩陣的譜補(bǔ)問(wèn)題有兩個(gè)基本內(nèi)容:一是缺項(xiàng)算子矩陣的譜擾動(dòng),即當(dāng)所缺的元素跑遍特定集合時(shí)所得算子矩陣的譜的交集,它是整個(gè)算子矩陣譜的穩(wěn)定的組成部分;二是缺項(xiàng)算子矩陣的可能譜,即當(dāng)所缺的元素屬于特定集合時(shí)所得算子矩陣的譜的并集,它反映了整個(gè)算子矩陣的譜的分布范圍.

設(shè)H1,H2,H3,H均為無(wú)窮維復(fù)可分Hilbert空間.以B(Hi,Hj)表示從Hi到Hj的所有有界線性算子構(gòu)成的集合,特別地,B(Hi)表示Hi上的所有有界線性算子構(gòu)成的集合,其中

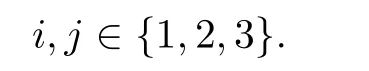
給定算子A∈B(H1),B∈B(H2),C∈B(H3),記

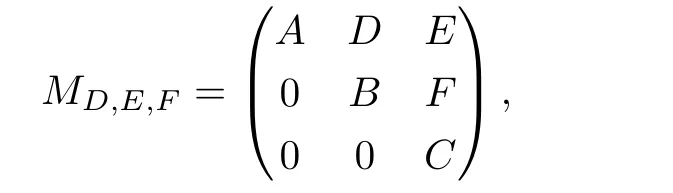
其中D∈B(H2,H1),E∈B(H3,H1),F∈B(H3,H2)為缺項(xiàng)的算子,則稱MD,E,F為H1⊕H2⊕H3上的3×3階缺項(xiàng)上三角算子矩陣.類似可有對(duì)給定算子A∈B(H1),B∈B(H2),記2×2階缺項(xiàng)上三角算子矩陣

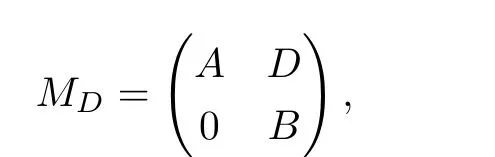
其中D∈B(H2,H1)為缺項(xiàng)的算子.

經(jīng)過(guò)近二十年的積累,2×2階上三角算子矩陣的譜補(bǔ)問(wèn)題研究已日臻完善,涌現(xiàn)出諸如譜,近似點(diǎn)譜,虧譜,本質(zhì)譜,Weyl譜,Browder譜,點(diǎn)譜,剩余譜以及連續(xù)譜等的補(bǔ)問(wèn)題結(jié)果[1-9].對(duì)于缺項(xiàng)3×3階上三角算子矩陣,文[10]描述了左(右)Fredholm譜擾動(dòng)以及Weyl型定理;文[11]研究了Moore-Penrose譜擾動(dòng);文[12]和[13]分別給出了點(diǎn)譜,剩余譜和連續(xù)譜的可能譜和擾動(dòng)的描述.文[14]研究了譜擾動(dòng)以及填洞問(wèn)題.此外,文[15]研究了四類點(diǎn)譜的擾動(dòng),文[16]研究了1,2類點(diǎn)譜和1,2類剩余譜的可能譜.本文繼續(xù)研究缺項(xiàng)3×3階上三角算子矩陣的譜補(bǔ)問(wèn)題,得到四類點(diǎn)譜的可能譜.需要指出的是:缺項(xiàng)3×3階算子矩陣的某些結(jié)論不能由2×2階情形直接推出,不是其簡(jiǎn)單推廣;文中對(duì)于點(diǎn)譜的分劃可參見(jiàn)[17],譜的這種細(xì)分劃對(duì)于討論算子矩陣的半群生成定理,譜包含性質(zhì)等具有一定的作用[18-19].

下面給出一些基本概念和輔助引理.對(duì)于算子T,分別以T?,N(T),R(T)表示T的共軛算子,零空間和值域,記n(T)=dimN(T),d(T)=dimN(T?).

定義1.1設(shè)X為Banach空間,T是X中的有界線性算子.稱集合

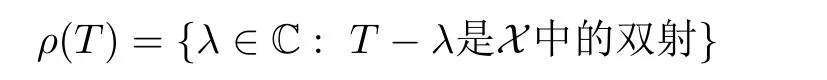
為T的預(yù)解集,預(yù)解集ρ(T)中的元素λ稱為T的正則值.稱集合σ(T)=Cρ(T)為T的譜.易知,T的譜σ(T)可分成互不相交的3個(gè)組成部分:

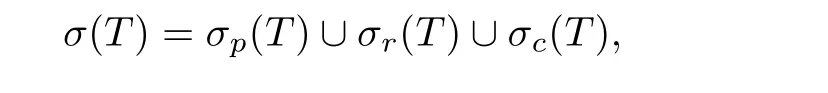
其中集合

分別為T的點(diǎn)譜,剩余譜和連續(xù)譜.此外,稱集合

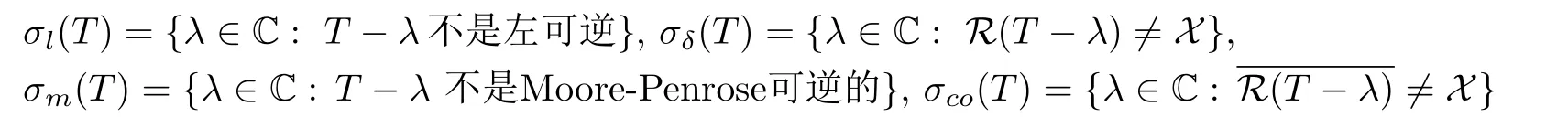
分別為T的左譜,右譜,Moore-Penrose譜,壓縮譜,并且為敘述方便記記ρin(T)=Cσp(T),ρ?(T)=Cσ?(T),其中σ?(T)∈{σl,σδ,σm,σco},ρ?(T)∈{ρl,ρδ,ρm,ρco}. 如所熟知,λ∈σm(T)當(dāng)且僅當(dāng)R(T?λ)不閉;λ∈ρl(T)當(dāng)且僅當(dāng)T?λ為具有閉值域的單射.類似于文[17],對(duì)點(diǎn)譜進(jìn)一步細(xì)分為

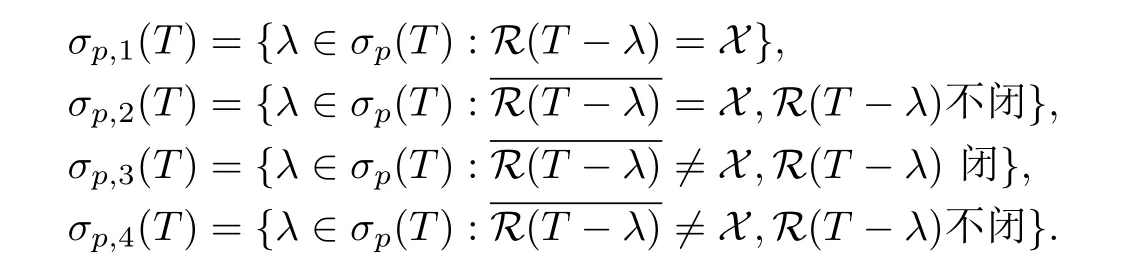
定義1.2設(shè)A∈B(H1),B∈B(H2),C∈B(H3)為給定算子,稱

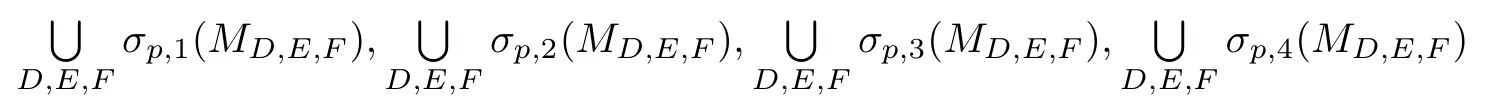
分別為缺項(xiàng)算子矩陣MD,E,F的1類可能點(diǎn)譜,2類可能點(diǎn)譜,3類可能點(diǎn)譜,4類可能點(diǎn)譜.

§2 主要結(jié)果及證明

不難看出λ∈σp,2(MD,E,F).若λ∈?43,則定義E=0且F形如(1),

易得λ∈σp,2(MD,E,F).

情形1λ∈σco(C)∪(ρin(A)∩ρin(B)∩ρin(C)).此時(shí)顯然任給D,E,F均有λ∈σco(MD,E,F)或者λ∈ρin(MD,E,F),從而λ/∈?.

情形2λ∈ρδ(C)且d(B?λ)>n(C?λ).此時(shí)對(duì)任意D,E,F算子矩陣MD,E,F?λ均有形如(3)的分塊形式,其中(C?λ)1為為可逆算子.注意到d(B?λ)>n(C?λ),易知無(wú)論如何選取算子D,E,F均有R(F22)不稠密,從而λ∈σco(MD,E,F).因此λ/∈?.

情形3λ∈ρδ(C)∩ρm(B)且d(A?λ)+d(B?λ)>n(B?λ)+n(C?λ).此時(shí)由定理2.1的情形5可知,對(duì)任意D,E,F均有λ∈σco(MD,E,F).因此λ/∈?.

情形4λ ∈ ρm(A)∩ρm(B)∩ρδ(C)且min{n(B?λ),d(A?λ)}<∞,min{n(C?λ),d(A?λ)}<∞且min{n(C?λ),d(B?λ)}<∞.此時(shí)任給D,E,F算子矩陣MD,E,F?λ均有如下分塊表示

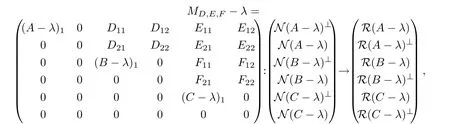
其中(A?λ)1,(B?λ)1,(C?λ)1均為可逆算子.因此,存在可逆算子U和V使得

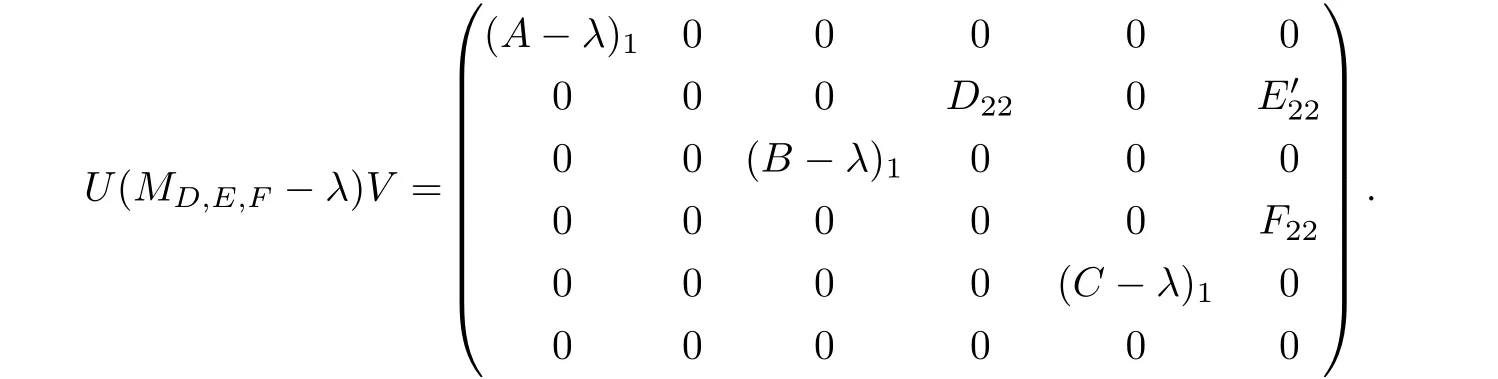
定理2.3設(shè)A∈B(H1),B∈B(H2),C∈B(H3)為給定算子,則

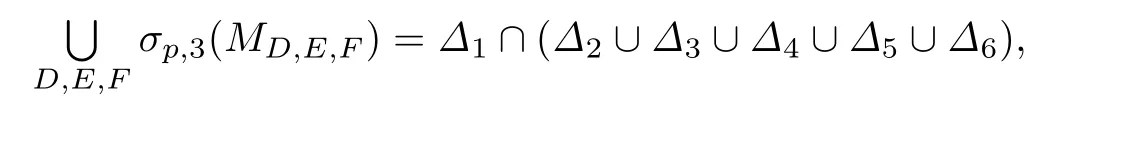
其中

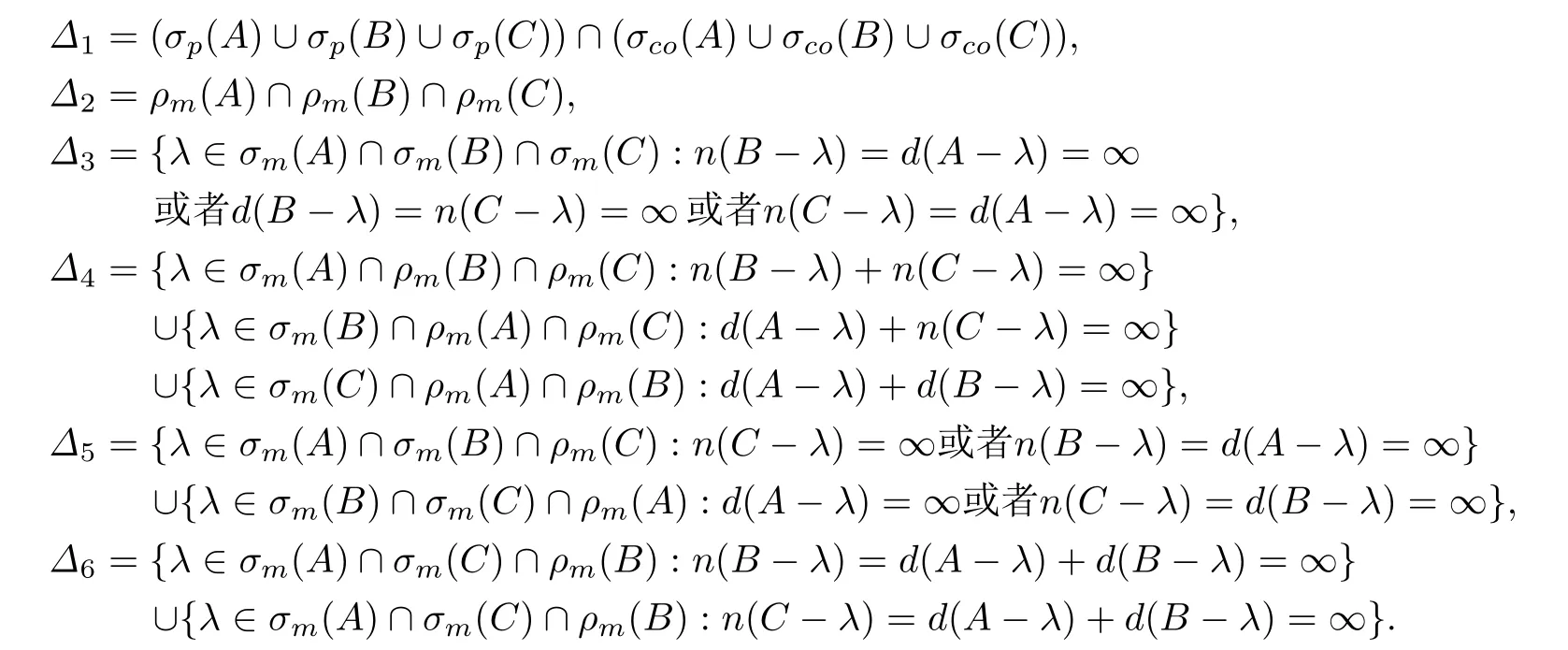
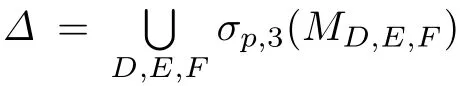
(1)設(shè)λ∈?1∩?2.定義算子D=0,E=0,F=0便得λ∈σp,3(MD,E,F).

(2)設(shè)λ∈?1∩?3.因?yàn)棣恕师襪(A)∩σm(B)∩σm(C),所以dimN(A?λ)⊥=dimN(B?λ)⊥=dimN(C?λ)⊥=∞.若n(B?λ)=d(A?λ)=∞,則定義E=0且

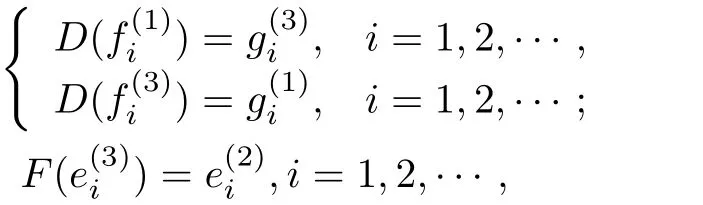
容易驗(yàn)證λ∈σp,3(MD,E,F).類似地可以證明當(dāng)d(B?λ)=n(C?λ)=∞或者n(C?λ)=d(A?λ)=∞時(shí),存在D,E,F使得λ∈σp,3(MD,E,F).

(3)設(shè)λ∈?1∩?4.現(xiàn)設(shè)λ∈?41.若n(B?λ)=∞,則定義E=0,F=0且

易得λ∈σp,3(MD,E,F).類似地可以證明當(dāng)λ∈?42∪?43時(shí),存在D,E,F使得λ∈σp,3(MD,E,F).

(4)設(shè)λ∈?1∩?5.現(xiàn)設(shè)λ∈?51.若n(C?λ)=∞,則定義D=0且

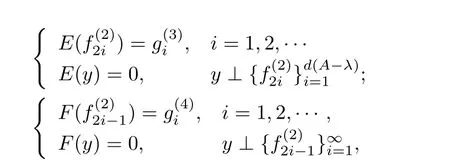
容易驗(yàn)證λ∈σp,3(MD,E,F).若n(B?λ)=d(A?λ)=∞,則取(2)中的D,E,F,從而λ∈σp,3(MD,E,F).類似地可以證明當(dāng)λ∈?52時(shí),存在D,E,F使得λ∈σp,3(MD,E,F).