Influence of toroidal rotation on the tearing mode in tokamak plasmas
Zhenghao REN (任政豪) , Jinyuan LIU (劉金遠), Feng WANG (王豐),4,Huishan CAI(蔡輝山),Zhengxiong WANG(王正洶) and Wei SHEN(申偉)
1 Key Laboratory of Materials Modification by Laser, Ion and Electron Beams (Ministry of Education),School of Physics, Dalian University of Technology, Dalian 116024, People’s Republic of China
2 Department of Engineering and Applied Physics, CAS Key Laboratory of Geospace Environment,University of Science and Technology of China, Hefei 230026, People’s Republic of China
3 Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, People’s Republic of China
Abstract The stabilizing mechanism of toroidal rotation on the tearing mode is studied using the 3D toroidal resistive magnetohydrodynamic code M3D.It is found that the dominating mechanism,either the centrifugal effect or the Coriolis effect,depends on the specific pressure β and rotation frequency Ω.On the premise that Ω is sufficiently large,when β is greater than a critical value,the effect of the centrifugal force is dominant, and the stabilizing effect mainly comes from the modification of equilibrium induced by the centrifugal force;when β is less than a critical value,the stabilizing effect from the Coriolis force overcomes that from the centrifugal force.However,if Ω is small, then the effect of equilibrium modification due to the centrifugal force is not significant even if β is large. Finally, the results showed that toroidal rotation shear enhances the stabilizing effect.
Keywords: tearing mode, toroidal rotation, resistive MHD(Some figures may appear in colour only in the online journal)
1. Introduction
The tearing mode (TM) is one of the most dangerous magnetohydrodynamic (MHD) instabilities, and can change the topology of the magnetic field, create magnetic islands, and increase local radial transport.Furthermore,the TM can produce a seed island, which triggers the neoclassical tearing mode(NTM).The NTM seriously influences plasma pressure and may cause disruption. Thus, suppressing the TM and understanding the mechanism are important for tokamak physics.
Neutral beam injection (NBI), as a primary auxiliary heating system in tokamaks, injects toroidal momentum and generates strong toroidal plasma rotation (in the following context,we use the shortened term ‘rotation’ to mean toroidal plasma rotation). It has been proven in experiments that rotation can affect MHD instabilities,including the TM[1,2].Experimental results of ASDEX Upgrade (the ‘Axially Symmetric Divertor Experiment’) showed that the onset threshold of the NTM increases with co- and counter-current direction rotation and with positive and negative rotation gradients [1]. However, in DIII-D, the experiments found that the effect of rotation on the NTM depends on the direction of the rotation [2]. Co-current rotation increases the 2/1 NTM onset threshold,while countercurrent rotation does not have a significant effect on the NTM.
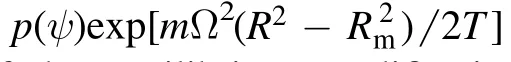




Figure 9. Magnitude of forces with Mq=2=0.27 when equilibrium modification is not considered: (a) perturbed centrifugal force and(b) perturbed Coriolis force.
β also affects the equilibrium and thus impacts the TM,so the stabilizing mechanism with different β is studied. To investigate the influence of β on the stabilizing mechanism,the rotation frequency Ω is kept fixed, and the results are shown in figure 10.
[γ(Ω=0.015, β)?γ(Ω=0, β)]/γ0reflects the effect of rotation, where γ(Ω=0.015, β) is the growth rate for Ω=0.015 rotation with β and γ(Ω=0,β)is the growth rate in the absence of rotation with the same β; a larger absolute value of [γ(Ω=0.015, β)?γ(Ω=0, β)]/γ0means a greater stabilizing effect. The blue diamonds represent the effect of the perturbed Coriolis on the TM.The red diamonds reflect the stabilizing effect from the perturbed Coriolis and centrifugal forces. The black diamonds include the perturbed Coriolis, perturbed centrifugal and equilibrium modification effects. By comparing the three lines in figure 10, when β is small (β=0.1%) the Coriolis effect has a greater stabilizing effect than the centrifugal force. When β?0.3%, the centrifugal effect including equilibrium modification is comparable with the Coriolis effect. Furthermore, as β increases,the effect of equilibrium modification becomes significant, and it is greater than the Coriolis effect when β is greater than the critical value. Based on both figures 10 and 8, it is necessary to note that the effect of equilibrium modification is related to β and Ω.On the premise that the rotation is sufficiently large,an increase in β will enhance the stabilizing effect of the equilibrium modification, and this effect can overcome the Coriolis effect when β is sufficiently large.However,when Ω is small, even if β is large, the effect of equilibrium modification is still not significant. The stabilizing effect of rotation is produced by the pressure–curvature term in addition to the toroidal coupling [29]. When β and Ω are large, the modification of equilibrium, particularly the pressure profile,produces a greater stabilizing effect on the TM.

Figure 10.Growth rate ratio [γ(Ω=0.015, β)?γ(Ω=0, β)]/γ0 versus β.
The results clarify the mechanism of rotation stabilizing the TM.The specific pressure β and rotation frequency Ω are two key parameters in the mechanism, which cause the different physical interpretations of the previous two simulation results in [4] and [5].
4. Conclusion
A global resistive MHD code (M3D) is used to study the influence of rotation on the m/n=2/1 TM. The simulation results show that the TM mode structure is changed by sheared rotation,and strong sheared rotation(Mq=2>0.3)significantly twists and broadens the classical TM structure. Rotation can stabilize the TM regardless of whether the rotation has shear; meanwhile,shear enhances the rotation’s stabilizing effect. The coupling of the centrifugal and Coriolis forces with the magnetic curvature contributes to the stabilizing effect of rotation. In addition, the centrifugal force can induce poloidal asymmetry of the equilibrium profile, which changes the tearing mode instability. This work clarifies the stabilizing mechanism of rotation on the TM.The results show that the effect of equilibrium modification induced by the centrifugal force depends on β and the rotation frequency Ω. If Ω is sufficiently large, then increasing β will enhance the stabilizing effect of equilibrium modification.
(1) When β is greater than a critical value, the effect of the centrifugal force is dominant, and the stabilizing effect comes mainly from the equilibrium modification induced by the centrifugal force,although the equilibrium modification is small.
(2)When β is less than a critical value,the Coriolis force has a greater stabilizing effect than the centrifugal force.
However, if Ω is not sufficiently large, then the effect of equilibrium modification is not significant even if β is large.
Acknowledgments
This work was supported by National Natural Science Foundation of China(Grant Nos.11975068 and 11605021),the National Key R&D Program of China(Grant No.2017YFE0301900),the Key Research Program of Frontier Science of Chinese Academy of Sciences (Grant No. QYZDJSSW-SYS016), and the Youth Innovation Promotion Association of CAS and the Fundamental Research Funds for the Central Universities (Grant No.DUT18ZD101).
ORCID iDs
Zhenghao REN (任政豪) https://orcid.org/0000-0002-9630-0395
 Plasma Science and Technology2020年6期
Plasma Science and Technology2020年6期
- Plasma Science and Technology的其它文章
- First-principles study on the mechanical properties and thermodynamic properties of Mo–Ta alloys
- Formation mechanism of Al2O3/MoS2 nanocomposite coating by plasma electrolytic oxidation (PEO)
- Estimation of the sheath power dissipation induced by ion cyclotron resonance heating
- Conversion between Vickers hardness and nanohardness by correcting projected area with sink-in and pile-up effects
- In-port-plug transmission line design of the ITER plasma position reflectometer
- Effects of the critical breakdown path on the ignition performance in heaterless hollow cathodes
