Xiaolong ZHU(朱霄龍),Feng WANG(王豐),Wei CHEN(陳偉),2 and Zhengxiong WANG(王正洶)

1 Key Laboratory of Materials Modification by Laser,Ion and Electron Beams(Ministry of Eduction),School of Physics,Dalian University of Technology,Dalian 116024,People’s Republic of China

2 Joint Laboratory for Fusion Product and Energetic Particles,Southwestern Institute of Physics,Chengdu 610041,People’s Republic of China

Abstract Based on the conventional tokamak HL-2A-like parameters and profiles,the linear properties and the nonlinear dynamics of non-resonant kink mode(NRK)and non-resonant fishbone instability(NRFB)in reversed shear tokamak plasmas are investigated by using the global hybrid kinetic-magnetohydrodynamic nonlinear code M3D-K.This work mainly focuses on the effect of passing energetic-ions on the NRK and NRFB instabilities,which is different from the previous works.It is demonstrated that the NRFB can be destabilized by the passing energeticions when the energetic-ion beta βh exceeds a critical value.The transition from NRK to NRFB occurs when the energetic-ion beta βh increases to above a critical value.The resonance condition responsible for the excitation of NRFB is interestingly found to be satisfied at ωt+ωp ≈ω,where ωt is the toroidal motion frequency,ωp is the poloidal motion frequency and ω is the mode frequency.The nonlinear evolutions of NRFB’s mode structures and Poincaré plots are also analyzed in this work and it is found that the NRFB can induce evident energeticion loss/redistribution,which can degrade the performance of the plasmas.These findings are conducive to understanding the mechanisms of NRFB induced energetic-ion loss/redistribution through nonlinear wave-particle interaction.

Keywords:energetic-ions,non-resonant fishbone,weak shear,loss/redistribution

1.Introduction

Achieving a steady state and long pulse operation of tokamak discharge has always been an important issue in the magnetically confined fusion study.The reversed magnetic shear(RMS)configuration,a key candidate of advanced scenario for International Thermonuclear Experimental Reactor(ITER),is really believed to be a promising scenario to realize this goal since that the internal transport barriers[1]might be triggered near the location of minimum of safety factorqmin,where the turblence transport is suppressed significantly and the high-performance plasmas can be obtained in the core regions[2-5].The recent experimental results obtained on different tokamaks in advanced scenarios with improved confinement and performance can be categorized according to theq-profile used for the regime as three categories[6]:(i)the first one includes scenarios with moderate reversed shear,i.e.with the difference betweenqminandq0,qon axis,less than ～2;(ii)the second category deals with high bootstrap fraction plasmas including strongly reversed shear plasmas;(iii)the third category refers to an advanced scenario with zero or low magnetic shear in the centre and safety factorqabove or near unity.

Usually,plasma configurations with shear reversal are prone to the excitation of reversed shear Alfvén eigenmode(RSAE)by energetic particles[7].However,the energetic particle mode,such as fishbone[8,9]and long-live mode[10,11],also can be excited in the RMS configuration.Both gap modes(such as RSAE)and continuum modes(such as fishbone)could result in significant energetic particle loss/redistribution thus affecting the first wall and the achievement of a high gainQfusin fusion plasmas[12].Fishbone,originated from its characteristic shape of the Mirnov magnetic signal,was first discovered in the poloidal divertor experiment(PDX)in 1980[13].To explain the experimental observation,several excited mechanisms were proposed in the past years.The first mechanism was proposed by Chenet althat the fishbone in PDX is excited by energetic trapped ions via precessional drift resonance[14].The second one was raised by Coppiet althat the mode frequency of fishbone,ω,is on the order of the thermal ion’s diamagnetic drift frequency ω*i[15].The third one was put forward by Fredricksonet althat the fishbone instability can be driven by the bounce motion of trapped energetic-ions[16].The fourth one was that the passing energetic particles can also drive such mode[17].Namely,the fishbones can be destabilized via wave-particle resonance interaction by energetic-ions produced from tangential[18]and perpendicular[13]neutral beam injection,including trapped[19]and passing[20]beam ions.In 2006,Fuet alused a fully self-consistent model including both particle and fluid nonlinearities to investigate the nonlinear dynamics of internal kink and fishbone instabilities and found that the nonlinear dynamics is mainly determined by the particle nonlinearity and the mode saturation is due to flattening of the particle distribution in the resonance region[21].Also,MEGA simulations showed that the fishbone on experimental advanced superconducting tokamak(EAST)can be simultaneously in resonance with the bounce motion of trapped particles and the transit motion of the passing particles[22].The low frequency fishbone instability can transit to a beta-induced Alfvén eigenmode when the energeticion beta increases to some critical threshold value[23].

In future burning plasmas,resonant fishbone losses are thought to be a concern because it is predicted that the alpha particles at relatively low energy(typical of few hundred keV)are able to be in resonance with fishbone(the characteristic frequencies are associated with the alpha particle’s energy and at high energy the alpha particle is difficult to enter resonance with a low frequency mode)[24].Except for resonant loss,the nonresonant losses of energetic-ions and fusion products induced by fishbones are found to be a pivotal issue as they can affect the higher energy population of fast alpha particles[25-27].Recently,the fishbone-induced transport of alpha particles has been investigated by Brochardet alvia the code XTOR-K under the two limits:the weak kinetic drive limit and strong kinetic drive limit,and it is found that the overall transport of alpha particles through theq=1 surface is of order 2%-5% of the initial population between the two kinds of simulations[28].

Fishbone has the features of strong bursting amplitude and rapid chirping-down frequency,and usually can lead to strong loss/redistribution of energetic-ions[18].The name of non-resonant internal kink mode(NRK)originates from its absence ofq=1 resonance surface of the safety factor profile.The NRK features saturated amplitude and slow frequency sweeping and has been observed experimentally on many tokamak devices,such as MAST[11],NSTX[29],HL-2A[30]and EAST[31].In Alcator C-Mod tokamak[32],it is demonstrated that NRK also can be destabilized by the nonresonant suprathermal electron pressure rather than by waveparticle resonance[33].In HL-2A,Yuet alfirst discovered that the NRK can be excited by energetic electrons with the reversed shearq-profiles formed and the value ofqmina bit larger than unity[30].Theoretically,the effects of toroidal rotation on NRK instability in NSTX plasmas were investigated using the extended MHD code M3D[34]by Wanget aland it is found that the plasma rotation at the experimental level has little effect on either equilibrium or linear stability but toroidal rotation can significantly influence the nonlinear dynamics of NRK and even can induce the(2,1)magnetic island[35].The nonlinear properties of NRFB instabilities excited by energetic ions are analyzed for weakly reversed shear tokamak plasmas and it is interestingly found that the radial displacement of NRFB weakly depends on the energetic-ion pressure and growth rate of the mode when theqprofile is flattened[36].From the dispersion relation of NRFB mode,the scaling law between the growth rate γ of the mode and energetic-ion beta βhunder the general reversed shear scenario is found to be satisfied atwhich is different from the scaling law γ ～βhunder the conventional positive magnetic shear scenario[37].However,it should be noted that these above results about the NRFB and NRK are mainly related with the non-conventional tokamaks.Few simulation studies of NRFB and NRK focused on the conventional tokamaks have been reported so far.This physical process of NRFB and NRK sometimes can induce sawtooth crash,causing significant energetic-ionloss/redistribution,and plays a key role in thermal plasma confinement,heliumash removal,α-particle heating and α-particle channeling[38,39]in future conventional tokamak burning plasma such as ITER.Therefore,based on the parameters and profiles in the conventional tokamak HL-2A,we perform the nonlinear global kinetic-hybrid simulations about the NRK and NRFB instabilities under the weakly RMS profiles in this work.

The remainder of this paper is organized as follows.Section 2 describes the global nonlinear kinetic-MHD model of M3D-K used in this work,the parameters and equilibrium profiles of our simulations.Section 3 gives the simulation results,including linear and nonlinear dynamics of NRK and NRFB,as well as the characteristics of loss/redistribution induced by NRK and NRFB instabilities.Section 4 presents the conclusion and discussion of this paper.

2.M3D-K model,equilibrium profiles and parameters setup

In this work,the nonlinear global hybrid kinetic-MHD simulation code M3D-K[21,34]is employed to self-consistently study the NRK and NRFB instabilities in conventional tokamak plasmas.The model in M3D-K is a fully nonlinear one with both the MHD nonlinearity and particle nonlinearity considered.In this kinetic-hybrid model,the bulk plasma is described by the resistive MHD equations and the energetic beam species are treated via drift-kinetic equations.The MHD equations are solved via finite element method poloidally and finite difference method toroidally.The energetic particle effect enters the MHD equation via pressure coupling and is calculated in a non-perturbative way.M3D-K code is a relatively mature and powerful simulation tool in the study of energetic particle physics of tokamak plasmas.The code so far has been effectively used to simulate toroidal Alfvén eigenmode(TAE),FB,RSAE,the resonant interaction between energetic particle and tearing modes,NRK on spherical tokamak and resistive internal kink mode[40-47].The multi-scale interaction between TAE and micro-turbulence was also studied using M3D-K code by Langet al[48].

The equilibrium profiles and physical parameters are chosen according to the conventional tokamak HL-2A in the work.Figure 1 shows the profiles of total pressurepand safety factorq.The main parameters used in the simulation are as follows:circular cross-section,aspect ratio?-1=R0/a=4.125,toroidal magnetic fieldB0=1.25 T,central plasma number densityn0=1.0×1019m-3,Alfvén speedAlfvén time τA=R/?vAand Alfvén frequency ωA=?vA/R0.The beam ion injection speed isvh=0.7vAin this simulation.The maximum gyro-radius of beam ions is ρh=0.07aforvh=0.7vA.The beam ion distribution function is chosen to be slowing down in energy and peaked in pitch angle Λ,where Λ is defined as Λ=μB/E,μ is the magnetic moment,Bis the magnitude of magnetic field at magnetic axis andEis the energy of beam ions.In the beam ion distribution,the central pitch angle is chosen to be Λ0=0.0,the width of pitch angle is set to be ΔΛ=0.3,the radial width isΔψ=0.3(ψmax-ψmin),and the critical velocity isvc=0.38vA.The detailed expression for distribution function can be referenced in these works[45,46,48].The plasma density profile is uniform in the simulations.It should be pointed out that this work is mainly concentrated on the passing energetic-ions driven NRFB and the effect of passing energetic-ions on the NRK.

Figure 1.Equilibrium profiles utilized in this work including the safety factor q profile(a)with the minimum value 1.014 at ψ=0.2506 and the total pressure profile p including the energeticion pressure pep and the bulk plasma pressure pb(b).It should be noted that the horizontal axis is the normalized poloidal flux ψ with ψ=0 corresponding to the magnetic axis and ψ=1 corresponding to the plasma edge.The pressure profile p is normalized by its value at the magnetic axis.

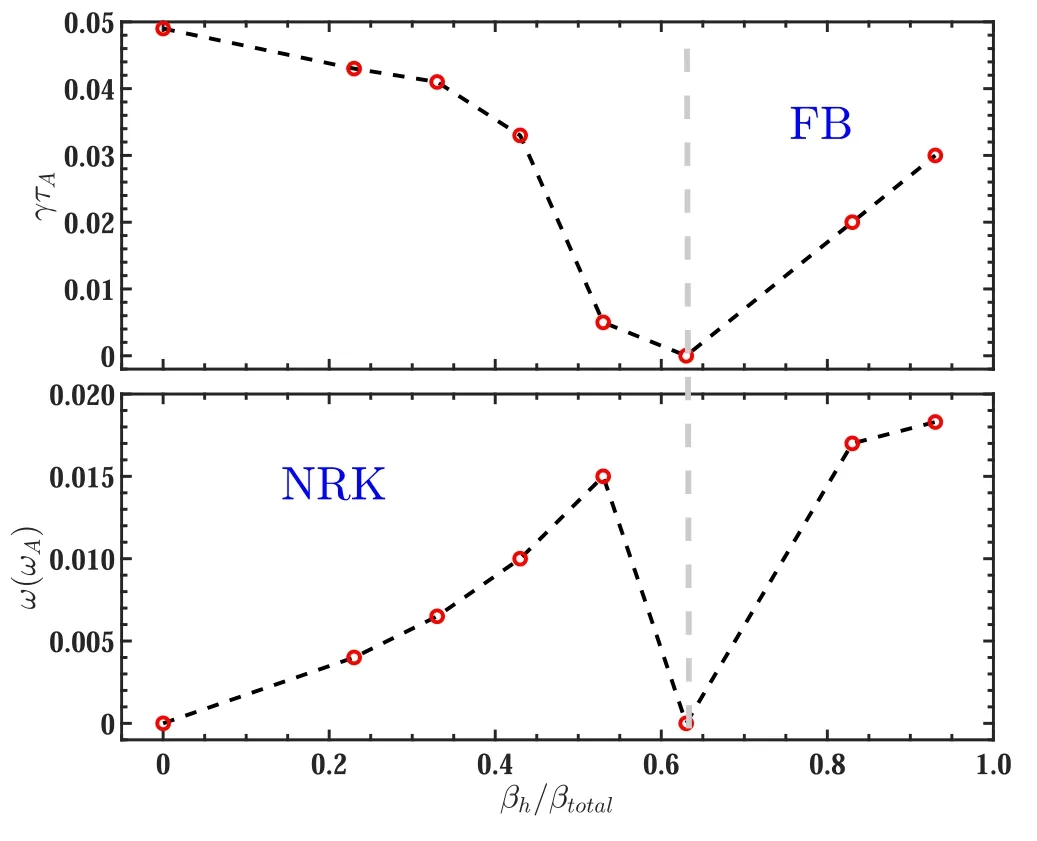
Figure 2.With respect to the NRK modes and fishbone instabilities,linear growth rate and mode frequency as a function of βh/βtotal,with qmin=1.014.The total pressure,including energetic-ion pressure and bulk plasma pressure,is fixed at βtotal=3.7%.The transition from NBK modes to NRFB instabilities is clearly observed in the simulation during the scan of βh/βtotal.

Figure 3.The mode structure U,velocity steam function,without energetic-ions(a)and with energetic-ions(b).The circles in the two figures(a)and(b)respectively denote the locations of the q=1.014 resonant surfaces.The energetic-ion beta in figure(b)is chosen as to be βh=3.37%.The horizontal axis R and vertical axis Z are both normalized by minor radius a.The mode structures of NRK and NRFB are ploted at the same toroidal angle φ=0.It is observed that the two mode structures are both located in the core region and are dominated by the(1,1)harmonic.

Figure 4.Linear growth rate and mode frequency as a function of the minimum value of safety factor qmin.It should be noted that during the scan of qmin,the q profile is only shifted up and down but the shape of q profile is kept fixed.The energetic-ion pressure fraction is fixed as βh/βtotal=0.43,and the total pressure is βtotal=3.7%.

Figure 5.The perturbed distribution function(δE)around the magnetic moment μ=0.254 in the phase space Pφ-E,where Pφ denotes the toroidal canonical momentum and E is the energetic-ion energy.Here,the mode frequency of NRFB ω is 0.019 89ωA.

3.Simulation results

3.1.Linear simulation results

In this section,the linear simulation results of then=1 mode with the above equilibrium profiles are presented.In order to obtain an unstable ideal NRK mode,we firstly perform the pure MHD simulation without energetic-ion effect.The growth rate and mode frequency are exhibited in figure 2.We can find that the NRK mode has a zero real frequency and relatively bigger growth rate at βh=0.The mode structure is demonstrated in figure 3(a)and the up-down symmetric structure located nearq=1.014 resonance surface corresponding to the minimum safety factorqminis clearly observed.Secondly,the energetic-ion effects on the NRK instabilities are studied via altering the energetic-ion pressure fraction βh/βtotalat fixed energetic-ion pressure βtotal=3.7% and the results are also shown in figure 2.It is found that with the increment of energetic-ion pressure fraction βh/βtotal,the growth rate of NRK mode gradually decreases while the mode frequency gradually increases.It is mainly due to the fact that the NRK mode is stabilized by the energetic-ion kinetic effect[49]and the energetic-ion kinetic effect becomes stronger with the increment of energetic-ion pressure fraction βh/βtotal.It should be noted that we mainly focus on the effect of passing energetic-ion effect on the NRK mode,which is different from the previous works[8,37,50].When the energetic-ion pressure fraction βh/βtotalincreases to a critical value,it is interestingly found that a mode transition from NRK mode to NRFB mode appears in the simulation,which has been clearly shown in figure 2.When we continue to increase the energetic-ion pressure fraction βh/βtotal,both growth rate and mode frequency of the NRFB mode increase.It can be attributed to the fact that the NRFB is intrinsically energetic-particle driven mode,whose drive is determined by the energetic-ion pressure gradient or distribution function gradient.The mode structureUof NRFB is shown in figure 3(b).Here,Uis the velocity stream function and related to the incompressible part of the plasma velocity by the expression:v=R2??⊥U×?φ+?χ+vφ?φ,whereRis major radius,?is the inverse aspect ratio,φ is toroidal angle,χ is the incompressible effect andvφis the toroidal velocity of plasmas.Compared to the ideal NRK mode,the NRFB mode structure becomes lightly twisted accompanied with a finite mode frequency.The extent of twist is connected with the intensity of energetic-ion effect.The two mode structures are demonstrated at the same toroidal angle φ=0.Thus,compared with the mode structure without energetic-ions as shown in figure 3(a),the finite rotation of mode structure for NRFB is triggered by the energetic-ion injection,which is clearly seen in figure 3(b).

In order to study the effect of minimum value of safety factor,qmin,on the NRK mode,we chose a case located on the region of NRK in the figure 2,where the energetic-ion pressure fraction is chosen as to be βh/βtotal=0.43 and the total pressure is fixed as βtotal=3.7%.It is found that the NRK mode’s stability is significantly sensitive to the minimum of safety factorqmin,which can be clearly seen in the figure 4.The growth rate γτAand mode frequency ω both decrease with the increment ofqmin.Whenqminincreases to 1.05,the NRK mode becomes stable.The NRK mode has a finite growth rate for the change of safety factor up to Δq=0.04,which means that there is still finite scope for an ideal internal mode to be driven unstable,even with the safety factorq＞1.These results related to the linear properties of NRK mode are consistent with the previous theoretical,experimental and numerical results[10,29,51].

The energetic-particle driven instabilities,such as fishbone modes,are generally excited by the free energy associated with the radial gradient of distribution function of energetic-ions via wave-particle resonance interaction.The resonance interaction is described as the expression:nωt+pωp=ω[52,53],wherenis the toroidal mode number of the perturbation,ωt=Δφ/Δt,ωp=Δθ/Δt,and Δtis the period time in poloidal space.For passing energetic-ions,the ωtis toroidal transit frequency,and ωpis poloidal transit frequency.Figure 5 shows the perturbed distribution function(δE)of energetic-ions around the magnetic moment μ=0.254 in the phase spacePφ-E,wherePφdenotes the toroidal canonical momentum andEis the energetic-ion energy.We choose μ=0.254 because the absolute value of δEis large.The blue and red regions shown in figure 5 represent δE＜0 and δE＞0,respectively.It is clearly observed that the waveparticle resonance interaction condition responsible for the excitation of the NRFB mode discussed here is ωt+ωp≈ω for co-passing energetic-ions and the main resonance condition is located near the region in phase space where the change of energetic-ion distribution function δEis significant.Interestingly,there are two resonance lines in the phase space responsible for the excitation of such NRFB mode,which have the same mathematical expression.The double resonance lines with the same resonance condition can be attributed to the reversed shearq-profile.Since the toroidal canonical momentumPφ,associated with the poloidal flux ψ,can be regarded as a radial variable,it can be clearly seen from figure 5 that the energetic-ions resonant with the NRFB mode are mainly located in the core,corresponding to the regions of smallPφ.

Figure 6.Time nonlinear evolution of kinetic energy and mode structures for n=1 NRFB mode.(a)Kinetic energy evolution,(b)t=263τA,in the early nonlinear phase and(c)t=563τA,in the late nonlinear phase.The red circles denote the q=qmin resonance surfaces,respectively.Notice that the case discussed here employs the same parameters as the figure 3(b).The linear eigenmode structure has been shown in the figure 3(b), t=183τA.

3.2.Nonlinear simulation results

In this section,the nonlinear evolutions of then=1 NRFB excited by co-passing energetic-ions with Λ0=0.0 are studied.Since numerical and theoretical works reported that the time evolutions ofn=1 NRFB mode in the absence and presence of MHD nonlinearity(namely mode-mode coupling)are similar,the simulations ofn=1 NRFB mode in this work are performed by forcing the MHD fluid response from bulk plasmas to be linear by only retaining then=1 toroidal perturbation in the initial run.Figure 6(a)shows the kinetic energy evolution of then=1 NRFB instability.Then=1 NRFB is first saturated att=263τA.Compared with the linear eigenmode structure shown in figure 3(b),the mode structure at the first saturated phase becomes more twisted and is located near theq=qminresonant surface represented by the red circle.In the late nonlinear phase,such ast=563τA,the mode structure is still twisted but becomes more broadened in radial direction.The broadened mode structure radially is close to the loss/redistribution of energetic-ions and this discussion will be performed in the next section.Furthermore,in comparison with the mode structure in early nonlinear phase,the mode structure inner theq=qminresonance surface shrinks at the late nonlinear phase,which can be clearly seen in figure 6(c).These results may be due to the two facts that:(1)theq-profile has evolved,which leads to the location of resonance surfaceq=qminto shift inwards;(2)the nonlinear effects of energetic-ions become significantly important in the late nonlinear phase.The energeticparticle driven instabilities are saturated via particle trapping in the nonlinear phase.Figure 7 shows the evolutions of Poincaré contours of magnetic field lines at the toroidal angle φ=0 plane.As we expected,the magnetic field lines exhibit regular state in the linear phase shown in the figure 7(a).When then=1 NRFB first saturates,the magnetic field lines become stochastic,especially in the central regions accompanied with the presence of chaos,which is demonstrated in the figure 7(b).Unfortunately,in the late nonlinear phase,the stochastic regions in the core furthermore extend radially.Stochasticity of magnetic field line is sufficiently large that the energetic-ion trajectories become stochastic and the confinement performance of energetic-ions then decreases.This may be the potential physical cause of the loss and redistribution of energetic-ions induced by then=1 NRFB discussed in this work.The transport,loss and redistribution of energetic-ions are of significant importance in the future magnetic confinement fusion reactor scale tokamaks.It is necessary to ascertain the underlying physics of NRFB induced energetic-ion loss/redistribution and then find out the measures to control and mitigate the destructive impacts on the fusion devices.Thus,in the next section,we analyze the loss/redistribution of energetic-ions induced by the nonlinear evolution of no-resonantn=1 fishbone instability.

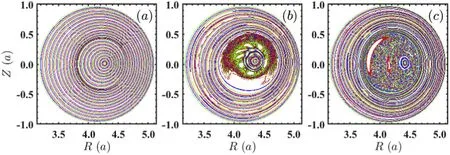
Figure 7.The Poincaré contours of magnetic surfaces at the toroidal angle φ=0 plane.(a)t=183τA,in the linear phase,(b)t=263τA,in the early nonlinear phase and(c) t=563τA,in the late nonlinear phase.

3.3.The redistribution and losses induced by NRFB

In this section,we analyze the loss/redistribution of energetic-ions induced by then=1 NRFB instability.Figure 8 shows the distribution functionfof energetic-ions around the magnetic moment μ=0.254.Figure 8(a)shows the initial distribution function of energetic-ions when we load the sample particles into the system.It can be clearly seen that the most energetic-ions are located at -0.3 ＜Pφ＜-0.22,0.2 ＜E＜0.32,near the innermost core.When the perturbation is relatively weak,the migration of the energetic-ions in phase space seems to be less massive,which usually can be seen in the linear phase.For a single mode,the motion of a particle in the phase space can be described as the formula dPφ/dt=-(ω/n)dE/dt,where ω is the mode frequency andnis the toroidal mode number of the perturbation.The loss/redistribution of energetic-ions induced by nonlinear evolution of then=1 NRFB mode are shown in the figures 8(b)and(c).Figure 8(b)shows the distribution function when the mode first saturates att=263τA.Figure 8(c)shows the distribution function in the late nonlinear phase,att=400τA.For the sake of convenience in comparison,we draw a vertical black dotted line atPφ=-0.24 in the panels(a)-(c).It should be noted that the same color bar is used in panels(a)-(c)so that we can easily compare the loss/redistribution induced by then=1 NRFB mode.It is found that by comparison the significant migration of energetic-ions from the core of the plasma to the edge of the plasma is clearly observed in the first saturated phase,and when then=1 NRFB mode arrives in the late nonlinear phase,att=400τA,the level of loss/redistribution further enhanced.In addition,the significant transport of energetic-ions in particle energyEdirection can be observed clearly during the nonlinear evolution of NRFB.Thus,the migration of energetic-ions in the phase space is very complicated.

Figure 8.Time evolution of energetic-ion distribution function f in Pφ-E space around the magnetic moment μ=0.254 at(a) t=0,(b) t=263τA,(c) t=400τA.The distribution functions around the energy E=0.31 shown by the horizontal black dotted line in panels(a)-(c)are compared in figure 9.In order to compare the loss/redistribution more clearly,the vertical black dotted line in panels(a)-(c)at Pφ=-0.24 is plotted.Here,the Pφ can be regarded as a radial variable.The larger Pφ corresponds to the edge of plasmas,which is labelled as EDGE.The smaller Pφ corresponds to the core of plasmas,which is labelled as CORE.Notice that we employ the same color bar in these panels in order to compare the level of loss/redistribution in the different phases of nonlinear evolution.

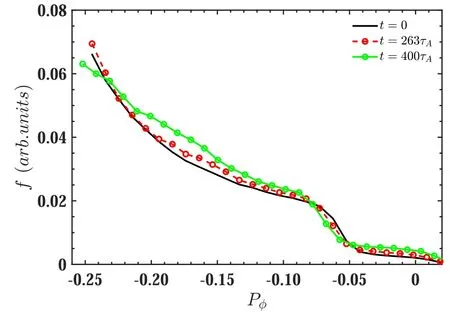
Figure 9.Time evolution of 1D distribution function around the magnetic moment μ=0.254 and the energy E=0.31 at t=0,t=263τA and t=400τA.

Figure 10.The frequency chirping phenomenon in the nonlinear simulation.

In figure 9,we compare the 1D energetic-ion distribution functionf(Pφ)around a constantE=0.254 along the horizontal dotted line drawn in the figures 8(a)-(c).On the slice ofE=0.254 we choose,the 1D distribution function variations between the initial phase and the first saturated phase are relatively small.It may be related with the specific energy slice we choose.However,in the late nonlinear phase att=400τA,the distribution functionfin the core corresponding to the smallerPφdecreases but the distribution functionfnear the edge corresponding to the largerPφis enhanced,for example in the regions of -0.2 ＜Pφ＜-0.1,-0.05 ＜Pφ＜0.It implies that the significant loss/redistribution can be induced by then=1 NRFB mode,especially in the late nonlinear phase since the saturated amplitude has the relatively large level.The overall loss fraction of energetic-ions induced by then=1 NRFB mode is calculated as a few percentage according to the simulation results.Much less data exists for lost particles in present HL-2A experiments,which limits the capacity of direct comparison between the numerical and experimental results.

The loss/redistribution of energetic-ion is a very important issue in the magnetic confinement fusion plasmas[54-57].Though in the case the loss fraction of energetic-ions is relatively small,only a few percentage,the mode-mode coupling between then=1 low frequency NRFB and the other MHD modes can trigger the energetic-ion avalanche transport and loss,which has been reported in the present experimental and theoretical studies.Thus,understanding then=1 low frequency NRFB induced energetic-ion loss/redistribution is of vital importance for the steady state operation of future fusion reactors,such as ITER.

In our nonlinear simulation,the frequency chirping phenomenon exists,which can be seen clearly in the figure 10.Frequency chirping is an evidence of resonant interaction between wave and energetic-ions.Also,frequency chirping can induce the resonance island shift in the phase space,which can partly explain the resonant energetic-ion losses in the single-n mode.The NRFB studied in this paper is a typical energetic-particle mode,of which the chirping rate is usually fast and the frequency chirps deeply into the continuum.Thus,these modes suffer the relatively large continuum damping and the sufficiently strong energetic-ion drive is needed.

4.Conclusion and discussion

In conclusion,based on the parameters and profiles in the conventional tokamak HL-2A,the global nonlinear kinetichybrid simulation code M3D-K has been employed to study the NRK andn=1 low frequency NRFB mode in the reversed shear tokamak plasmas.This work mainly focuses on the passing energetic-ions driven NRFB and the effect of passing energetic-ions on the NRK.The NRK mode is firstly obtained and the up-down symmetric mode structure located nearqmin=1.014resonance surface is clearly observed,which proves that the mode we obtain here is really NRK mode.Secondly,we study the energetic-ion effects on the NRK instabilities by altering the energetic-ion pressure fraction βh/βtotalat fixed energetic-ion pressure βtotal=3.7%.A mode transition from NRK mode to NRFB mode is interestingly observed when the energetic-ion pressure fraction βh/βtotalincreases to a critical value.Compared to the ideal NRK mode,the linear eigenmode structure of NRFB mode becomes lightly twisted accompanied with a finite mode frequency.The NRK mode’s stability is significantly sensitive to the minimum of safety factorqmin.These results related to the linear properties of NRK mode are consistent with the previous theoretical,experimental and numerical results.The wave-particle resonance interaction condition responsible for the excitation of then=1 low frequency NRFB mode is ωt+ωp≈ω for co-passing energetic-ions.Interestingly,there are two resonance lines in the phase space responsible for the excitation of such NRFB mode,which have the same mathematical expression.The nonlinear simulation results reveal that the mode structure at the first saturated phase becomes more twisted and is located near theq=qminresonant surface and in the late nonlinear phase,the mode structure becomes more broadened in radial direction.The evolutions of Poincaré contours of magnetic field lines at the toroidal angle φ=0 plane are analyzed.When then=1 NRFB first saturates,the magnetic field lines become stochastic,especially in the central regions accompanied with the presence of chaos.Furthermore,in the late nonlinear phase,the stochastic regions in the core furthermore extend radially.The loss/redistribution of energetic-ions induced by then=1 NRFB instability are also analyzed.It is found that by comparison the significant migration of energetic-ions from the core of the plasma to the edge of the plasma is clearly observed in the first saturated phase,and when then=1 NRFB mode arrives in the late nonlinear phase,att=400τA,the level of loss/redistribution further enhanced.We also compare the 1D energetic-ion distribution functionf(Pφ)around a constantE=0.254 and find that the significant loss/redistribution can be induced by then=1 NRFB mode,especially in the late nonlinear phase since the saturated amplitude has the relatively large level.The overall loss fraction of energetic-ions induced by then=1 NRFB mode is calculated as a few percentage according to the simulation results.Much less data exists for lost particles in present HL-2A experiments,which limits the capacity of direct comparison between the numerical and experimental results.Though in the case the loss fraction of energetic-ions is relatively small,only a few percentage,the mode-mode coupling between then=1 low frequency NRFB and the other MHD modes can trigger the energetic-ion avalanche transport and loss,which has been reported in the present experimental and theoretical studies.Thus,understanding then=1 low frequency NRFB induced energetic-ion loss/redistribution is of vital importance for the steady state operation of future fusion reactors,such as ITER.

Acknowledgments

We acknowledge HL-2A team measurements for their support of these experiments and the Supercomputer Center of Dalian University of Technology for providing computing resources.This work was supported by National Natural Science Foundation of China(Nos.11 925 501,11 975 068 and 11 835 010),China Postdoctoral Science Foundation(No.2021M700674)and the Fundament Research Funds for the Central Universities(No.DUT21GJ205).