章月紅,劉 偉,蔣望東

(紹興文理學(xué)院元培學(xué)院數(shù)學(xué)教研部,浙江紹興312000)

§1 引 言

從數(shù)學(xué)和物理學(xué)的角度分析,無慣性神經(jīng)網(wǎng)絡(luò)系統(tǒng)可理解為超阻尼(阻尼趨向無窮大)的模型,當(dāng)阻尼超過臨界值時(shí)其每個(gè)神經(jīng)元狀態(tài)的動力性質(zhì)也將改變.因此在實(shí)際問題中也要考慮有阻尼(弱阻尼)情況下神經(jīng)網(wǎng)絡(luò)的動力性質(zhì).于是慣性神經(jīng)網(wǎng)絡(luò)日趨受到廣大學(xué)者的認(rèn)同,其動力學(xué)行為的研究頗受關(guān)注.如:文[1-3]分別研究了單個(gè)慣性時(shí)滯神經(jīng)元網(wǎng)絡(luò)的分岔,混沌和周期解的穩(wěn)定性.文[4]研究慣性時(shí)滯兩神經(jīng)元系統(tǒng)的動力.[5]研究了具有時(shí)滯的慣性神經(jīng)網(wǎng)絡(luò)的反周期解的穩(wěn)定性.[6-7]分別研究具有變時(shí)滯脈沖慣性神經(jīng)網(wǎng)絡(luò)和復(fù)雜神經(jīng)網(wǎng)絡(luò)的全局收斂性問題.[8-9]對于具有變時(shí)滯慣性神經(jīng)網(wǎng)絡(luò)在拉格朗日意義上的全局指數(shù)穩(wěn)定和指數(shù)穩(wěn)定分別得到研究.在[10-11]中,對于慣性Cohen-Grossberg型神經(jīng)網(wǎng)絡(luò)分別研究其平衡點(diǎn)穩(wěn)定性和周期解指數(shù)穩(wěn)定.[12]對于一類具有Leakage時(shí)滯慣性Cohen-Grossberg神經(jīng)網(wǎng)絡(luò)的全局指數(shù)穩(wěn)定性和的Hopf分支給出了判定條件.[13]研究了馬爾可夫跳躍參數(shù)慣性Cohen-Grossberg神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性.對于慣性BAM神經(jīng)網(wǎng)絡(luò)動力行為的研究也有不少結(jié)果如文獻(xiàn)[14-19].在[20-21]利用非降階方法分別得到慣性神經(jīng)網(wǎng)絡(luò)周期新的結(jié)果和動力學(xué)分析新的研究.在實(shí)際中,系統(tǒng)除了受到阻尼(慣性)因素干擾外,還會受到隨機(jī)因素的干擾,而對隨機(jī)神經(jīng)網(wǎng)絡(luò)各種類型動力行為的研究較為成熟,已有不少成果.如參考文獻(xiàn)[22-23]對隨機(jī)細(xì)胞神經(jīng)網(wǎng)絡(luò)穩(wěn)定性分別進(jìn)行了討論,[24-25]對隨機(jī)Hop field神經(jīng)網(wǎng)絡(luò)分別給出均方指數(shù)穩(wěn)定和周期解,[26-29]對隨機(jī)神經(jīng)網(wǎng)絡(luò)分別給出了穩(wěn)定性結(jié)果,[30]討論了隨機(jī)時(shí)滯遞歸神經(jīng)網(wǎng)絡(luò)穩(wěn)定問題,在文[31]中,討論了隨機(jī)擴(kuò)散Cohen-Grossberg型BAM神經(jīng)網(wǎng)絡(luò)周期解穩(wěn)定性,[32-33]分別討論了隨機(jī)Cohen-Grossberg神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性和指數(shù)同步,[34]研究隨機(jī)擾動神經(jīng)網(wǎng)絡(luò)的脈沖控制等等.

眾所周知,實(shí)際應(yīng)用必須建立在系統(tǒng)的穩(wěn)定性之上,所以考慮兩個(gè)因素同時(shí)干擾下的神經(jīng)網(wǎng)絡(luò),即隨機(jī)慣性神經(jīng)網(wǎng)絡(luò)穩(wěn)定性在理論和應(yīng)用上都具有研究價(jià)值.從作者所查閱信息資料所知,到目前為止,對于既含有隨機(jī)項(xiàng)又同時(shí)包含慣性項(xiàng)的神經(jīng)網(wǎng)絡(luò)模型穩(wěn)定性研究尚未見到相關(guān)文獻(xiàn).本文將討論在現(xiàn)有的神經(jīng)網(wǎng)絡(luò)模型中同時(shí)添加隨機(jī)和慣性項(xiàng),研究一類隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)穩(wěn)定性問題,它將是一個(gè)較有新意的研究課題.同時(shí)通過引入合適的變量替換,將二階微分系統(tǒng)變換為一階微分系統(tǒng),利用隨機(jī)微分方程有關(guān)性質(zhì)和遞推歸納,給出判定其系統(tǒng)平衡點(diǎn)存在唯一及全局漸近穩(wěn)定和解指數(shù)穩(wěn)定的充分條件,得到新的研究成果,這將對其系統(tǒng)在理論上探究和實(shí)際應(yīng)用都具有一定意義.

對于一類慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)

如果在系統(tǒng)(1)中加上隨機(jī)擾動項(xiàng),得到一類隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)

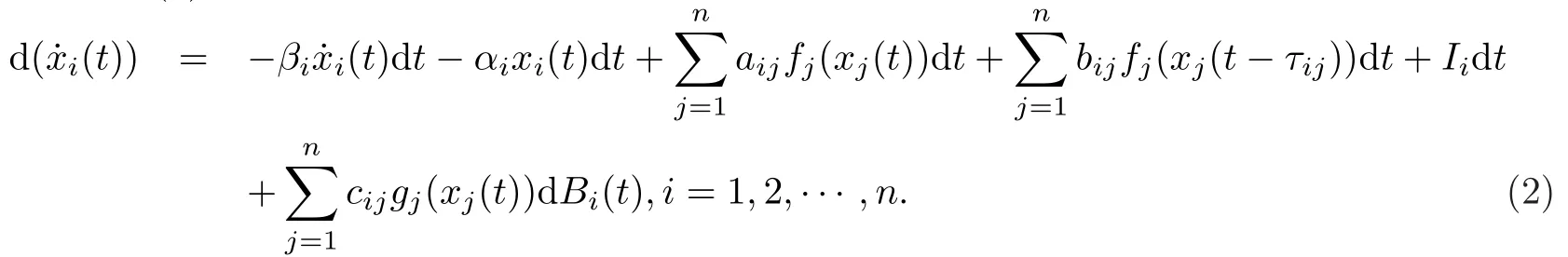
其中xi(t)表示系統(tǒng)狀態(tài);βi>0為阻尼(慣性)系數(shù),αi>0為常數(shù);aij,bij表示輸出反饋權(quán)值;τij≥0表示時(shí)間時(shí)滯;fj(xj(t))表示系統(tǒng)輸出;Ii表示系統(tǒng)的閾值或偏項(xiàng);cijgj(xj(t))dBi(t)表示隨機(jī)擾動,并且B(t)=(B1(t),B2(t),···,Bn(t))T是定義在完備概率空間(?,R,P)上具有自然濾波{Rt}t≥0的n維Brownian運(yùn)動.

給定(2)的初始條件

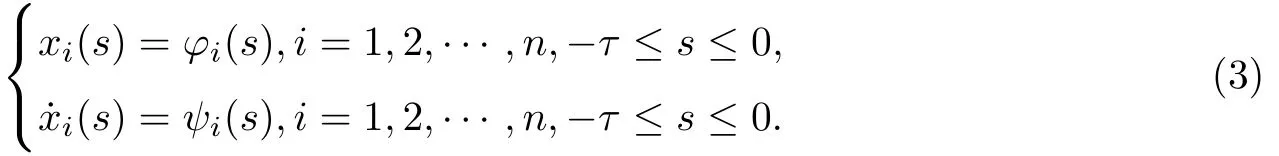
其中?i(s),ψi(s)是有界連續(xù)函數(shù),而

本文主要研究系統(tǒng)(2)平衡點(diǎn)隨機(jī)全局漸近穩(wěn)定和解指數(shù)穩(wěn)定的問題,并給出其判定的充分條件.

§2 預(yù)備知識

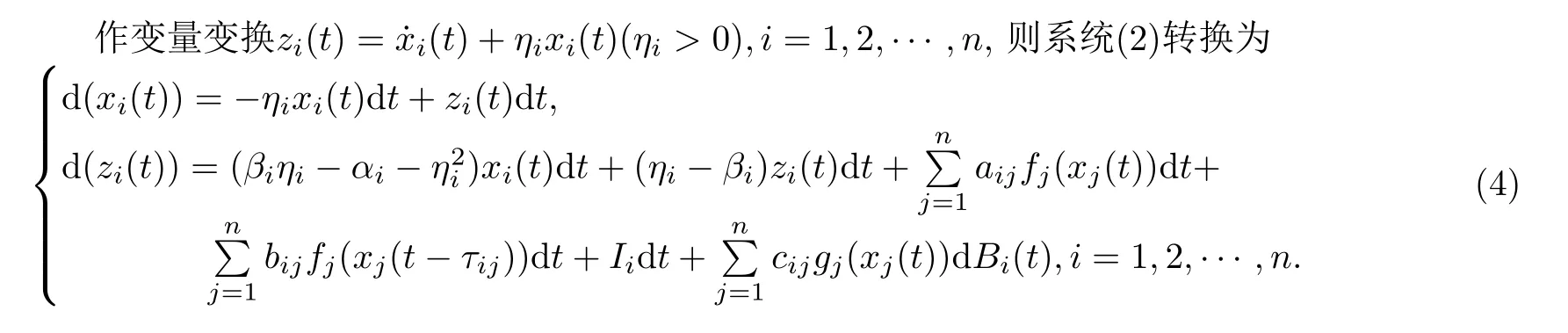
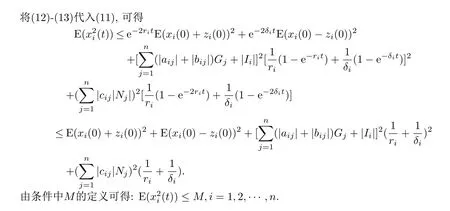
§3 主要結(jié)果

注 本文主要討論一類隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)穩(wěn)定性問題,并給出其系統(tǒng)平衡點(diǎn)存在唯一及全局漸近穩(wěn)定和解指數(shù)穩(wěn)定判定條件,即得到定理3.1-定理3.3新的研究成果.與作者所查閱到的現(xiàn)有文獻(xiàn)結(jié)果比較,他們所研究的結(jié)果只是在神經(jīng)網(wǎng)絡(luò)模型中單一加上慣性項(xiàng)如參考文獻(xiàn)[1-21],或者在神經(jīng)網(wǎng)絡(luò)模型中單一加上隨機(jī)項(xiàng)如參考文獻(xiàn)[22-34],即他們僅考慮在各類神經(jīng)網(wǎng)絡(luò)模型系統(tǒng)中只含有慣性或者隨機(jī)項(xiàng)單一因素的干擾.而本文研究的問題既考慮到含有慣性項(xiàng)又考慮到含有隨機(jī)項(xiàng),在兩個(gè)因素同時(shí)干擾的情況下研究一類隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)系統(tǒng)平衡點(diǎn)和解的穩(wěn)定性問題.從數(shù)學(xué),物理理論知識上分析,慣性項(xiàng)的出現(xiàn)使神經(jīng)網(wǎng)絡(luò)具有更加復(fù)雜的動力學(xué)性態(tài),它是導(dǎo)致系統(tǒng)出現(xiàn)分叉和混沌的一個(gè)主要因素.另一方面,隨機(jī)因素是客觀存在不可避免的,系統(tǒng)運(yùn)行時(shí)常常會受到隨機(jī)因素的干擾,例如控制上的變化,觀察中的誤差,乃至傳感器噪聲.因此,在神經(jīng)網(wǎng)絡(luò)模型中同時(shí)增加隨機(jī)和慣性項(xiàng),將二者結(jié)合能模擬更為復(fù)雜的網(wǎng)絡(luò)系統(tǒng),也是對現(xiàn)有的神經(jīng)網(wǎng)絡(luò)系統(tǒng)的豐富與完善,是一個(gè)值得去探討的新課題.本文得到的研究成果,將對其系統(tǒng)設(shè)計(jì)的探索和實(shí)際應(yīng)用的實(shí)現(xiàn)提供了理論上的判據(jù).

§4 數(shù)值例子

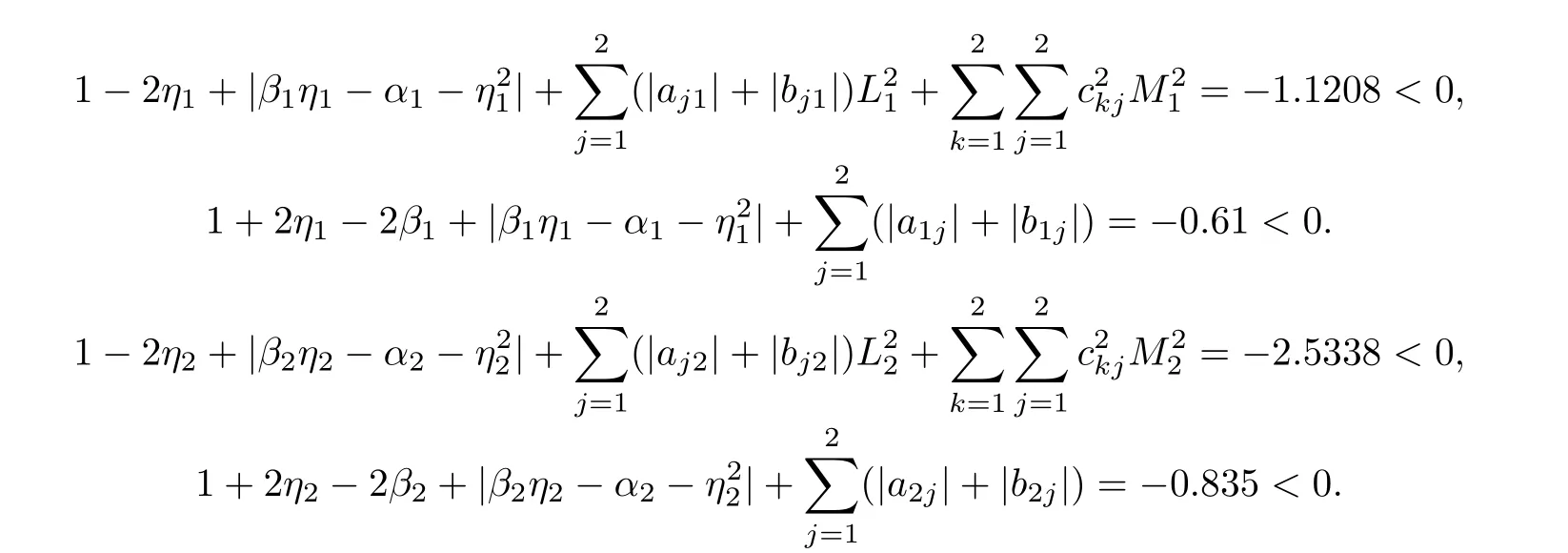
可知系統(tǒng)(22)滿足定理3.2的條件,由定理3.2可知(22)的唯一平衡點(diǎn)是隨機(jī)全局漸近穩(wěn)定的,計(jì)算可得平衡點(diǎn)為(π,π).另一方面,任意給出四組初始值:

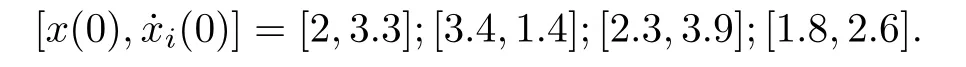
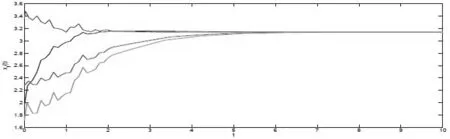
圖 1 例4.1狀態(tài)變量x1(t)的瞬時(shí)響應(yīng)

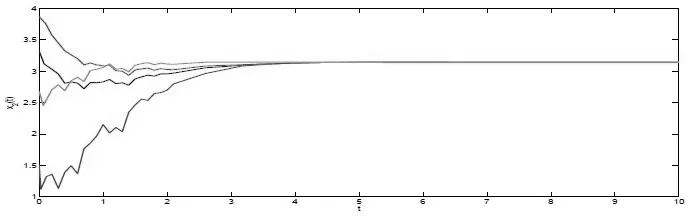
圖 2 例4.1狀態(tài)變量x2(t)的瞬時(shí)響應(yīng)

通過數(shù)值模擬得到例4.1狀態(tài)變量x1(t),x2(t)的瞬時(shí)響應(yīng)圖1-2.顯然,從圖可知其模擬結(jié)果與定理3.2理論推導(dǎo)結(jié)論相一致.

取η1=4,η2=5,Li=0.2,Mi=0.2.經(jīng)計(jì)算系統(tǒng)(23)滿足引理2.4和定理3.3的條件,由定理3.3知,系統(tǒng)(23)的解是指數(shù)穩(wěn)定的.另一方面,任意給出四組初始值:

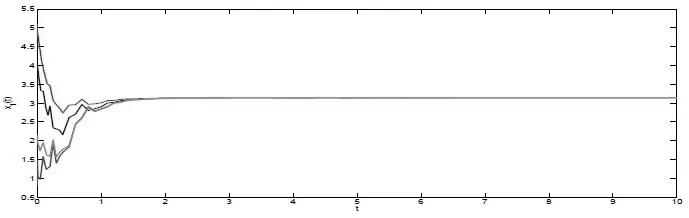
圖 3 例4.2狀態(tài)變量x1(t)的瞬時(shí)響應(yīng)

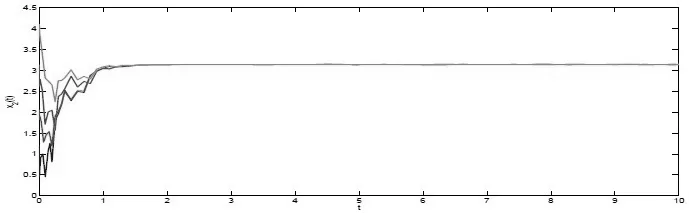
圖 4 例4.2狀態(tài)變量x2(t)的瞬時(shí)響應(yīng)

通過數(shù)值模擬得到例4.2狀態(tài)變量x1(t),x2(t)的瞬時(shí)響應(yīng)圖3-4.顯然,從圖可知定理3.3理論推導(dǎo)結(jié)論與其模擬結(jié)果一致,說明所得理論結(jié)果的正確性.

§5 結(jié)論

隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)既考慮了阻尼因素,又考慮了隨機(jī)干擾因素.因此,與單一研究慣性神經(jīng)網(wǎng)絡(luò)穩(wěn)定性或隨機(jī)神經(jīng)網(wǎng)絡(luò)穩(wěn)定性在理論和應(yīng)用上更具有研究價(jià)值.在本文中,研究了系統(tǒng)(2)隨機(jī)慣性時(shí)滯神經(jīng)網(wǎng)絡(luò)平衡點(diǎn)隨機(jī)全局漸近穩(wěn)定性和解指數(shù)穩(wěn)定性,給出了其穩(wěn)定性判定的充分條件,對于實(shí)際應(yīng)用和理論的探討具有一定的意義.同樣,利用本文的討論思路和方法,可進(jìn)一步研究其他類型的隨機(jī)慣性神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性問題,如:隨機(jī)慣性Cohen-Grossberg神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性,隨機(jī)慣性BAM神經(jīng)網(wǎng)絡(luò)的穩(wěn)定性等.