任光震

(浙江大學數(shù)學科學學院,浙江杭州310027)

§1 引 言

自上世紀下半葉以來,Twistor理論取得了豐富的成果和長足的進展.Twistor理論是由Penrose在研究四維時空中的場方程引入的.具體地,首先給出閔科夫斯基空間與三維復射影空間CP3的一種對應(yīng),該對應(yīng)即為著名的Twistor變換,借助該變換可以將閔科夫斯基空間上的很多場方程的解表示為CP3中某類開子集上的齊次全純函數(shù)的軌道積分,該積分就是著名的Penrose-積分公式.Penrose積分公式具有廣泛的應(yīng)用,例如在某些復空間或四元數(shù)空間上,相應(yīng)的Penrose型積分公式即為Cauchy-Fueter方程的解(見[1]-[8]).Baston和Eastwood用復幾何和表示論將Twistor變換推廣到一般的G/P空間上,其中G為半單李群,P為其拋物子群(見[9]).本文從表示論的角度研究四元Heisenberg群上的Twistor理論.并考慮四元Heisenberg群上的切向k-Cauchy-Fueter方程(見[10]-[13]),給出其解即為四元Heisenberg群上的Penrose型積分公式.

§2介紹了李代數(shù)sp(2n+4,C)中的拋物子代數(shù).利用[14]的方法給出了李群Sp(2n+4,C)關(guān)于各拋物子群陪集的坐標卡.§3通過介紹各拋物子代數(shù)及相關(guān)Dynkin-圖的雙纖維化,給出各拋物子群陪集的雙纖維化,進而得到四元Heisenberg群上的Twistor變換.§4給出了四元Heisenberg群上的Penrose型積分公式,證明了該積分公式可以給出很多非平凡的k-CF函數(shù).

§2 預備知識

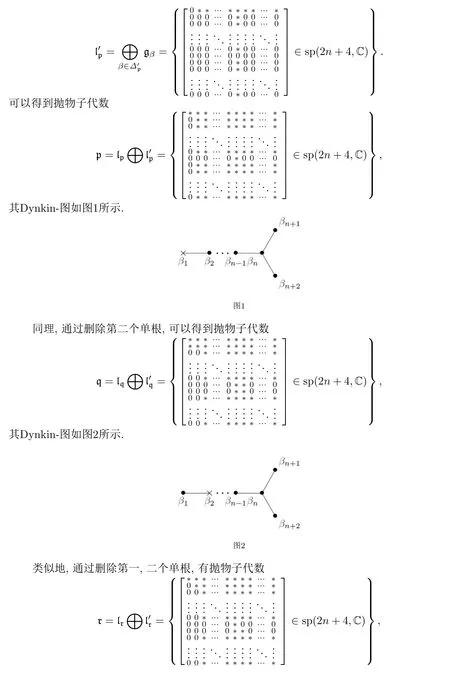
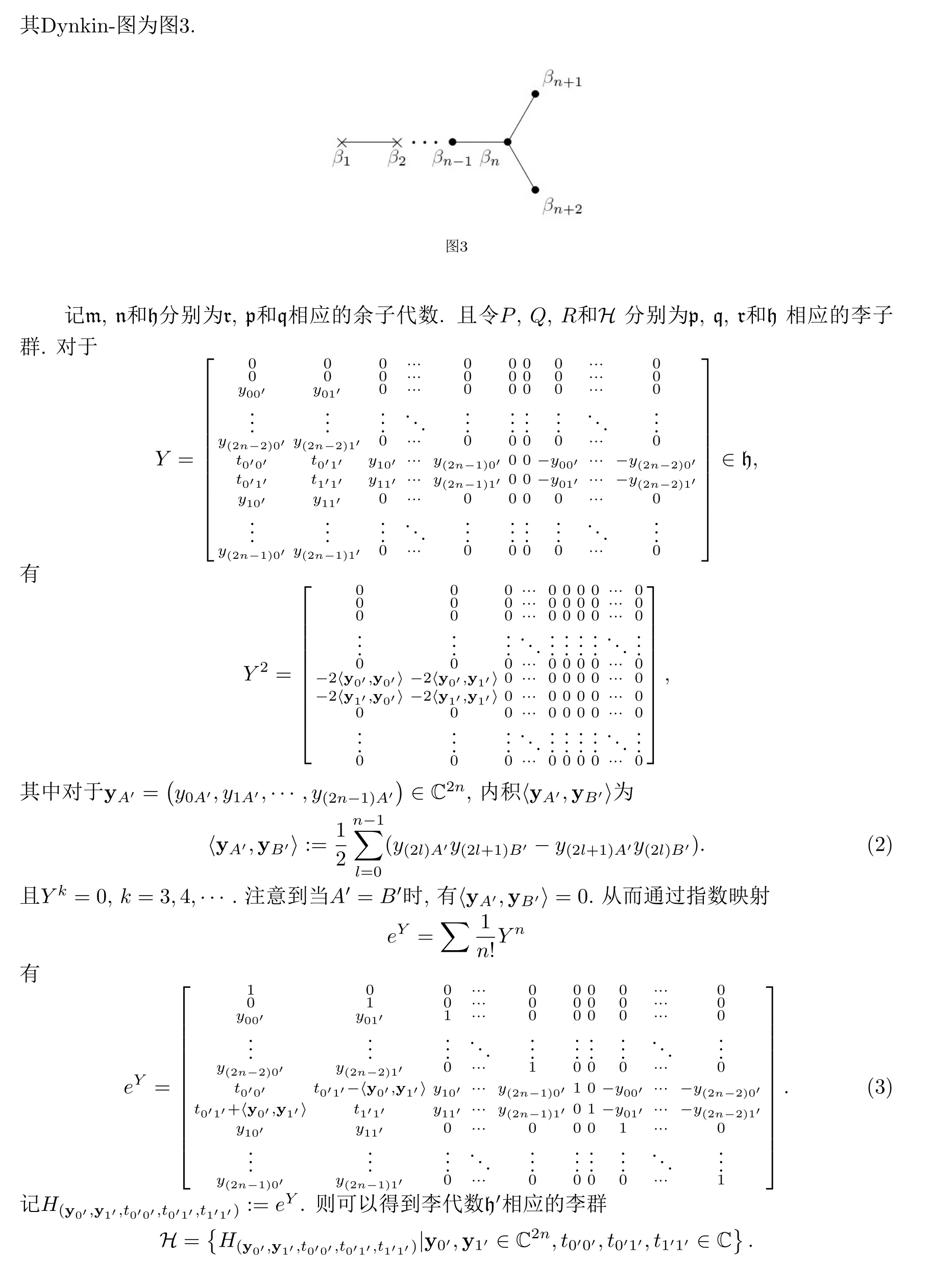
§3 Twistor-變換

本節(jié)將借助sp(2n+4,C)中拋物子代數(shù)的的雙纖維化(如圖4所示),

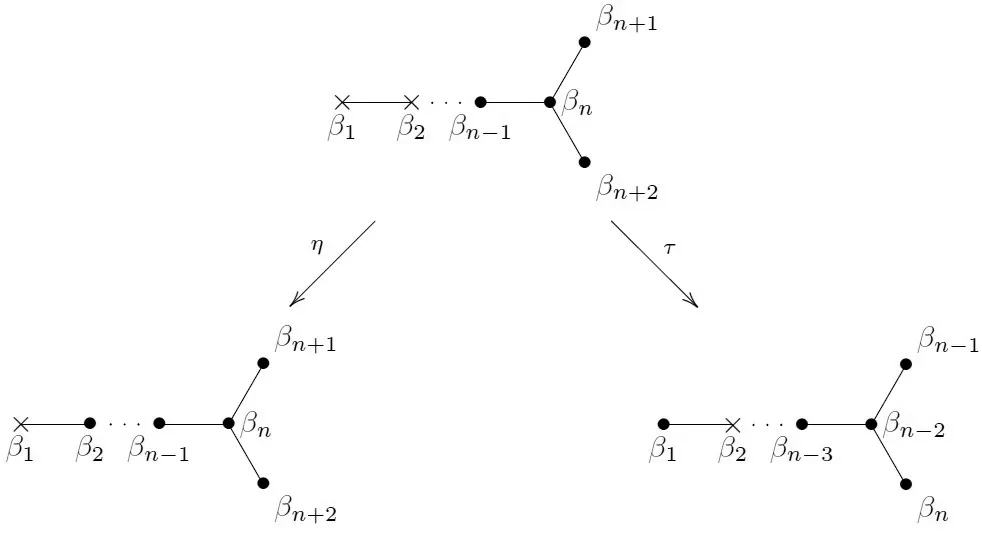
圖4

§4 Penrose-積分公式和四元k-CF多項式