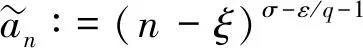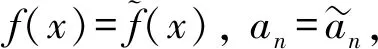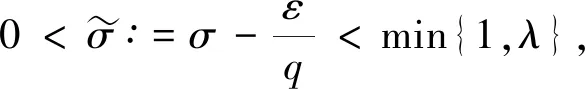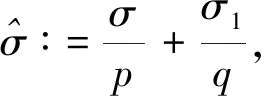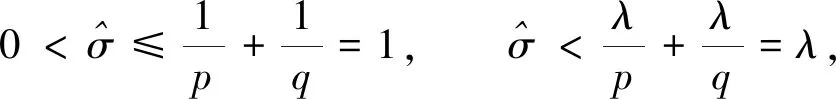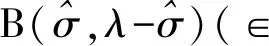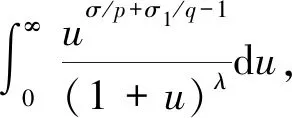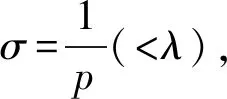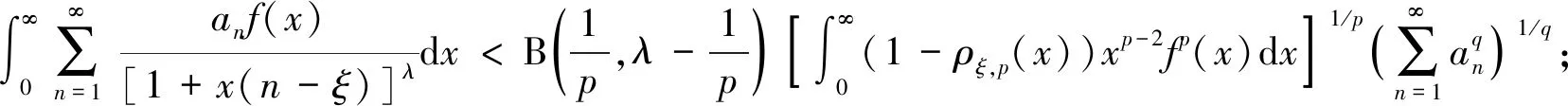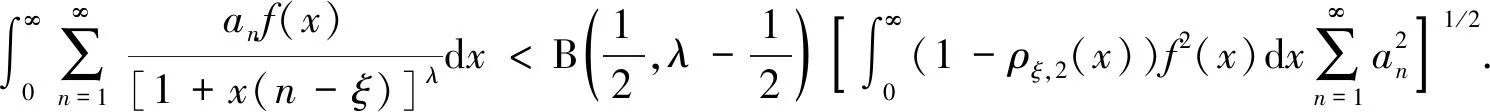辛冬梅, 楊必成

(廣東第二師范學(xué)院 數(shù)學(xué)系, 廣州 510303)

0 引 言

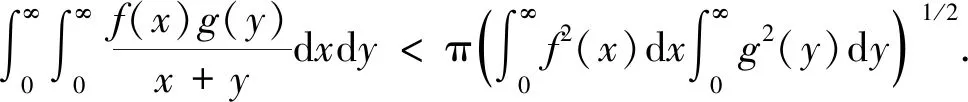
(1)

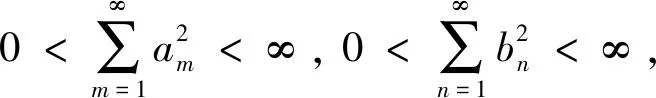
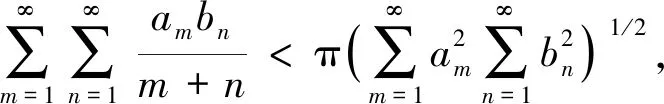
(2)

這里, 常數(shù)因子π均為最佳值. 式(1)和式(2)是分析學(xué)中的重要不等式[2-4].

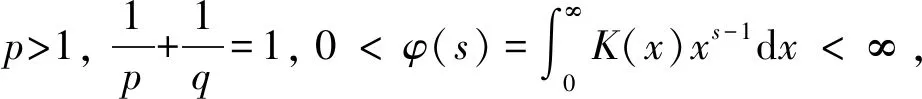
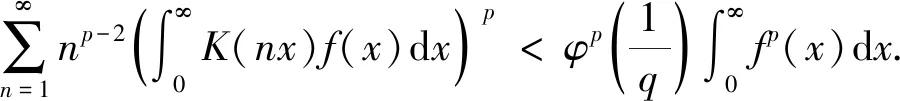
(3)

文獻[5-8]給出了式(3)的若干推廣和應(yīng)用; 文獻[9-10]討論了式(1)和式(2)一般推廣形式的常數(shù)因子取最佳值聯(lián)系參數(shù)的等價性質(zhì); 文獻[11]討論了如下半離散非齊次核Hilbert不等式：

的最佳常數(shù)因子聯(lián)系參數(shù)σ,σ1(∈(0,1]∩(0,λ))的等價性質(zhì), 其中

是Beta函數(shù).

本文參考文獻[9]方法, 應(yīng)用權(quán)函數(shù)及Hermite-Hadamard不等式, 建立式(4)的一個較精確且加強型的不等式, 并給出該不等式常數(shù)因子取最佳值聯(lián)系參數(shù)的一組等價性質(zhì)及一些特殊參數(shù)不等式.

1 引 理

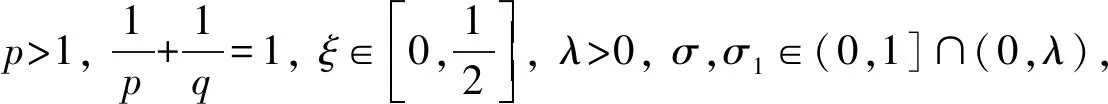
又設(shè)f(x)≥0(x∈+=(0,∞)),an≥0(n∈={1,2,…}), 使得

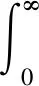
引理1若權(quán)函數(shù)

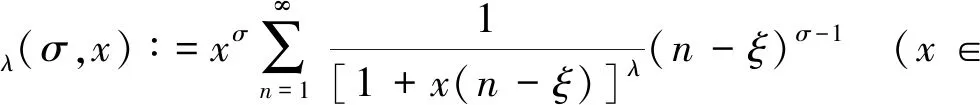
(5)

則有如下雙邊不等式

B(σ,λ-σ)(1-O1(xσ))

(6)

其中：

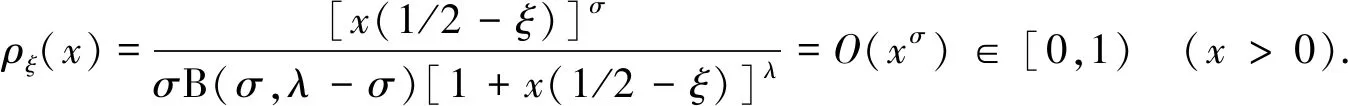
(7)

證明： 固定x>0, 設(shè)

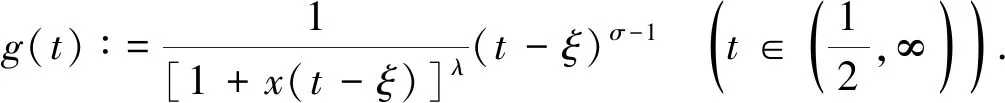
這里,ρξ(x)如式(7). 事實上, 有

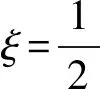
故式(6)成立. 證畢.

引理2下列不等式成立:

證明： 對于n∈, 做變換u=x(n-ξ), 可求得下列權(quán)函數(shù):

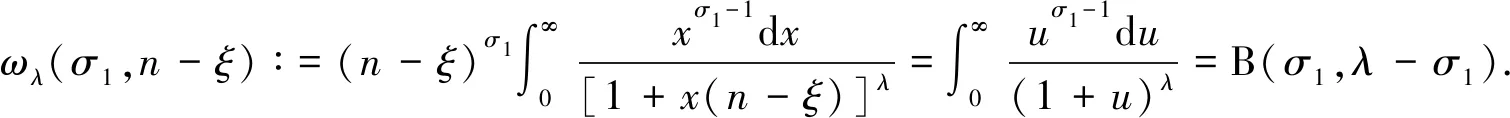
(9)

由H?lder不等式[12], 有

再由式(6),(9), 有式(8). 證畢.

注1因ρξ(x)≥0, 故由式(8)可導(dǎo)出如下非加強型不等式:

特別地, 取ξ=0, 式(10)即變?yōu)槭?4). 因而式(8)是式(4)的較精確的加強型不等式.

2 主要結(jié)果

若σ1=σ∈(0,1]∩(0,λ), 則式(8)變?yōu)槿缦潞啙嵭问?

定理1式(11)的常數(shù)因子B(σ,λ-σ)是最佳值.

證明： 任給0<ε

這里,

由式(6), 因

故還可得

從而可得不等式:

令ε→0+, 由Beta函數(shù)的連續(xù)性, 有B(σ,λ-σ)≤M. 故M=B(σ,λ-σ)是式(11)的最佳值. 證畢.

且式(8)變形為

定理2若式(12)的常數(shù)因子B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是最佳值, 則σ1=σ.

由H?lder不等式[12], 有

且式(13)取等號的充分必要條件是存在不全為0的常數(shù)A,B, 使得Auσ-1=Buσ1-1a.e.于+. 不妨設(shè)A≠0, 于是有于+, 即有σ-σ1=0. 故σ1=σ. 證畢.

定理3下列陳述等價:

1) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)與p,q無關(guān);

2) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)可表示為一個單積分;

3) B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是式(8)的最佳值;

4)σ1=σ.

證明: 1) ? 2). 由于B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)與p,q無關(guān), 故

其為一個單積分.

4) ? 1). 因σ1=σ, 故

B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)=B(σ,λ-σ),

與p,q無關(guān).

4) ? 3). 由定理1知, B1/p(σ,λ-σ)B1/q(σ1,λ-σ1)是式(12)(即式(8))的最佳值.

3) ? 4). 由定理2有σ1=σ.

故陳述1)～4)等價. 證畢.

則有不等式

(14)

則有不等式

(16)

上述不等式的常數(shù)因子都是最佳值.