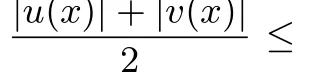浙江省寧波效實(shí)中學(xué)(315012) 童益民

含兩個(gè)絕對(duì)值的函數(shù)的最值問(wèn)題,是平常教學(xué)中經(jīng)常碰到的題型,比如求含兩個(gè)絕對(duì)值的函數(shù)的最小值,很容易想到用絕對(duì)值不等式,有些題很方便的就可以做出來(lái),用此方法是否都可以解決這類(lèi)題目,很多同學(xué)沒(méi)有很清楚的認(rèn)識(shí).同樣,求含兩個(gè)絕對(duì)值的函數(shù)的最大值,又可以怎么解決,本文對(duì)此類(lèi)問(wèn)題進(jìn)行研究,試圖得到比較全面的認(rèn)識(shí).

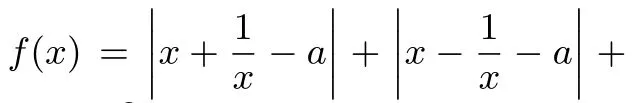
解根據(jù)絕對(duì)值不等式,|a|+|b|≥|a±b|,類(lèi)比可得,|u(x)|+|v(x)|≥|u(x)±v(x)|.

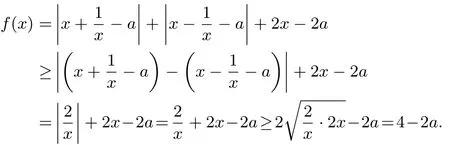
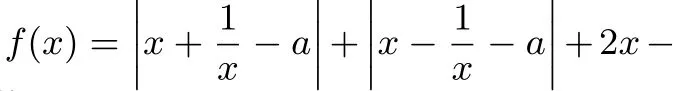
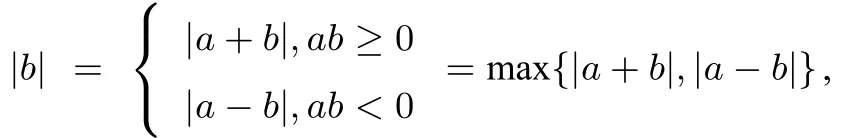
(1)當(dāng)a≤0時(shí),如圖1,函數(shù)f(x)的最小值在x=x0處取到,由可得所以f(x)min=f(x0)=4x0-4a=-2a.

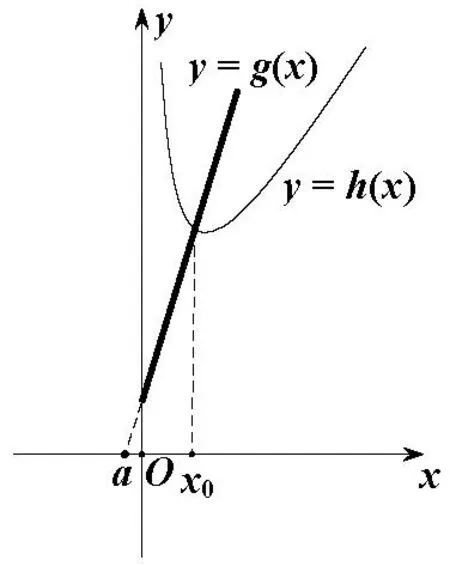
圖1

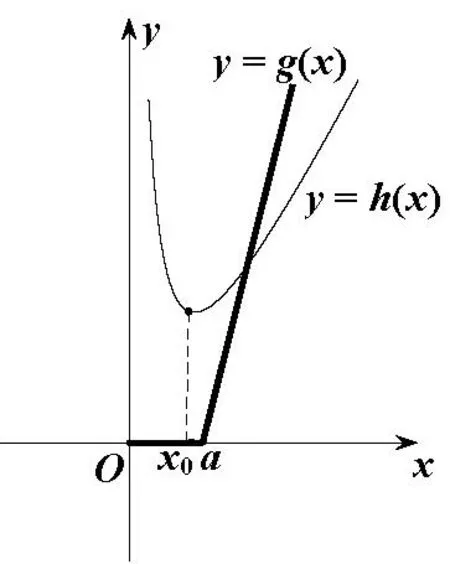
圖2

(2)當(dāng)a＞0時(shí),

(i)0＜a＜2時(shí),如圖2,函數(shù)f(x)的最小值在x=x0處取到,此時(shí)x0=1,所以f(x)min=f(1)=4-2a.

(ii)a=2時(shí),如圖3,函數(shù)f(x)的最小值在x=x0處取到,此時(shí)x0=1,所以f(x)min=f(1)=0.

(iii)a＞2時(shí),如圖4,當(dāng)x1≤x≤x2時(shí),函數(shù)f(x)取到最小值為0.綜上,由(1)(2)得,

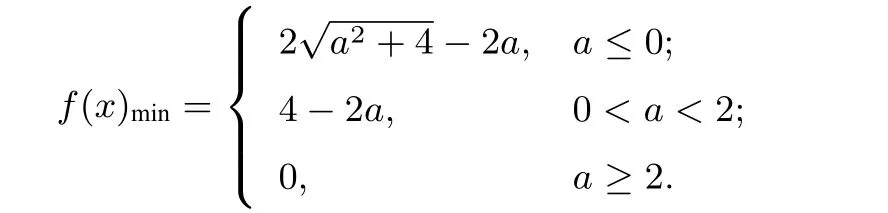
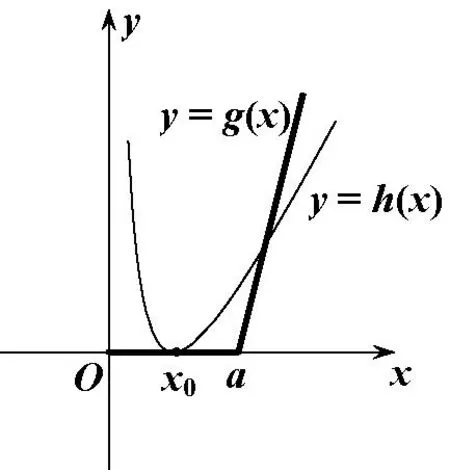
圖3

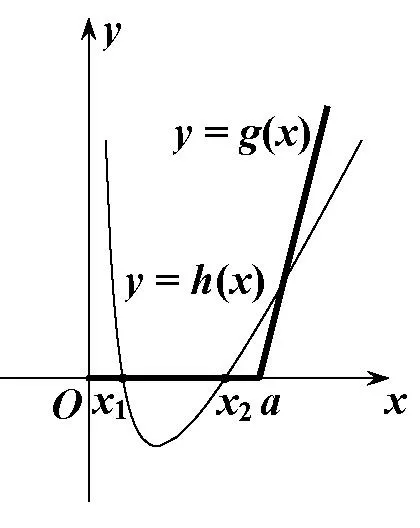
圖4

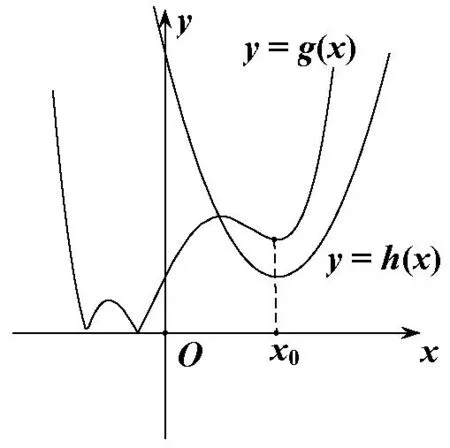
圖5

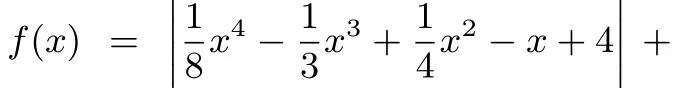
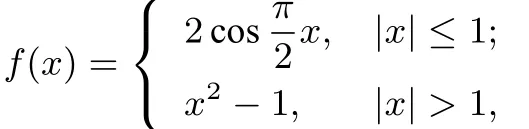
解令F(x) =|f(x)+f(x+l)-2|+|f(x)-f(x+l)|,所以F(x)= max{|2f(x)-2|,|2f(x+l)-2|},若對(duì)任意實(shí)數(shù)x,max{|2f(x)-2|,|2f(x+l)-2|}≥2恒成立,即對(duì)任意實(shí)數(shù)x,|f(x)-1|≥1或|f(x+l)-1|≥1恒成立,(注意,上式不等價(jià)于對(duì)任意實(shí)數(shù)x, |f(x)-1|≥1恒成立,或?qū)θ我鈱?shí)數(shù)x,|f(x+l)-1|≥1恒成立),畫(huà)出g(x)=|f(x)-1|的圖像,通過(guò)h(x)=|f(x+l)-1|圖像的平移,如圖6,可得,即l的最小值為

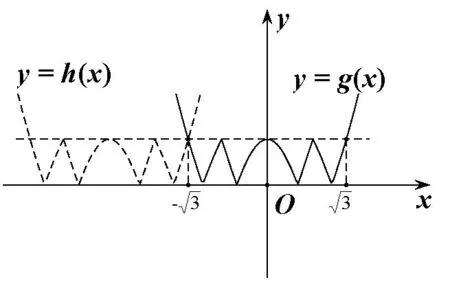
圖6

題3若函數(shù)f(x)=|asinx+bcosx-1|+|bsinxacosx|(a,b∈R)的最大值為11,求a2+b2的值.

解1f(x)=|asinx+bcosx-1|+|bsinx-acosx|=max{|(a+b)sinx+(b-a)cosx-1|,|(a-b)sinx+(b+a)cosx-1|}≤max{|(a+b)sinx+(b-a)cosx-1|max,|(a-b)sinx+(b+a)cosx-1|max}=max{+1,}+1=+1,所以+1=11,所以a2+b2=50.

注意,解1中用到了(max{|g(x)|,|h(x)|})max=max{|g(x)|max,|h(x)|max},此等式顯然是成立的.

解2

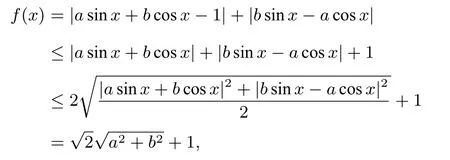
當(dāng)|asinx+bcosx|=|bsinx-acosx|且asinx+bcosx≤0時(shí),兩等號(hào)同時(shí)成立.所以+1=11,所以a2+b2=50.