呂艷春

(廣西師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院,廣西 桂林541006)

0 引言及主要結(jié)果

考慮以下的邊值問題

在文獻(xiàn)[2]中,Chu,Hai和Shivaji利用解的估計(jì)和反證法得到了(1)在滿足Dirichlet邊界條件下的正徑向解的唯一性,還得到了解的漸進(jìn)性.注意到,在文獻(xiàn)[2]中(1)在u=0處可能具有無限半正定結(jié)構(gòu),且不要求f是單調(diào)的.文獻(xiàn)[3]研究了(1)在半正定條件下(f(0)＜0)的正經(jīng)向解的唯一性,且要求f是單調(diào)的.此外,文獻(xiàn)[2-3]所得到的結(jié)果都要求λ?1.對(duì)于當(dāng)λ?1時(shí)的唯一性結(jié)果還可以參見文獻(xiàn)[4-6,8].

文獻(xiàn)[8]研究以下邊值問題的正解的存在性與唯一性：

其中0≤α＜1,c：[0,∞)→(0,∞),h：(0,1)→(0,∞)都是連續(xù)函數(shù),且λ是一個(gè)正參數(shù).該文在對(duì)f和h的一些假設(shè)條件下,利用上下解的方法得到了問題(3)在λ?1時(shí)至少有一個(gè)正解,并且還證明了問題(3)在α=0時(shí)有唯一正解.對(duì)于當(dāng)λ?1時(shí)的存在性結(jié)果還可以參見文獻(xiàn)[1,9,11].

我們對(duì)f(z)和h(t)作如下假設(shè)：

注意到在(H5)的條件下,問題(2)在u=0處可能具有無限半正定結(jié)構(gòu).特別地,若(H1)～(H3)成立,問題(2)在λ?1時(shí)至少有一個(gè)正解.[8]

在上述假設(shè)條件下,得到主要結(jié)果如下：

定理1：假設(shè)(H1)～(H5)成立,則當(dāng)λ＞λ0時(shí),問題(2)有唯一正解.

1 一些引理

本節(jié)介紹一些在定理1的證明中將要用到的引理.

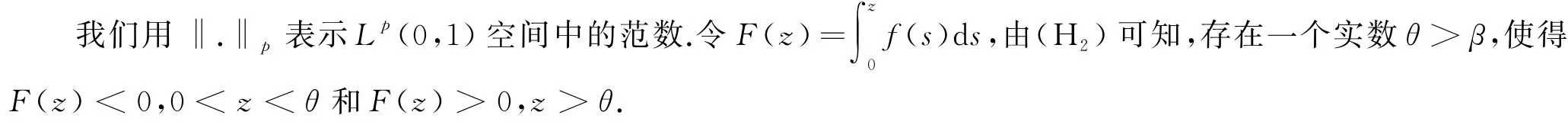
引理1[7,11]對(duì)?x,y∈?,當(dāng)1＜p＜2時(shí),有

當(dāng)p≥2時(shí),有|?-1(x)-?-1(y)|≤2?-1(|x-y|).

引理2[2]令u(t)是(2)的一個(gè)正解,則u(t)在(0,1)內(nèi)有唯一的最大值,記為u(t0),且u(t0)≥θ.

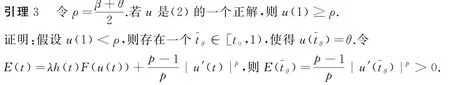
因?yàn)閡(t)在[t~θ,1]上遞減,所以u(píng)(t)≤θ,t∈[~tθ,1],從而有E'(t)=λh'(t)F(u(t))≥0,

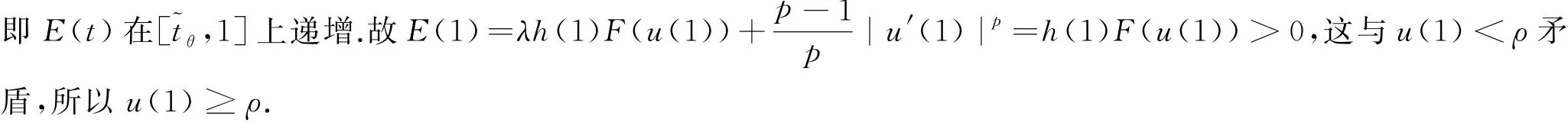
引理4[2]令tρ∈(0,t0)使得u(tρ)=ρ,則存在一個(gè)常數(shù)cρ＞0,使得(2)的任何一個(gè)正解u(t)滿足

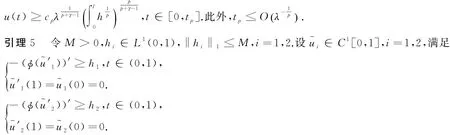
則 (i)給定一個(gè)ε0＞0.如果h2≥0,h2?0,且存在常數(shù)δ＞0,使得‖h1-h2‖1＜δ,則有

證明：令ui∈C1[0,1],i=1,2,滿足

由弱比較原理(見文獻(xiàn)[10]的Lemma A.2)得,~u1(t)≥u1(t),u2(t)≥~u2(t),?t∈[0,1].令ε＞0.下面證明若存在δ＞0,使得‖h1-h2‖＜δ,則‖u'1-u'2‖∞＜ε.

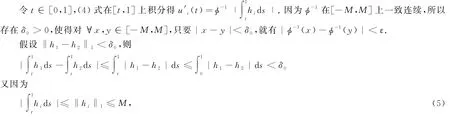
所以|u'1(t)-u'2(t)|＜ε,t∈[0,1].因此,只要取δ=δ0,這就證得若存在δ＞0,使得‖h1-h2‖1＜δ,則‖u'1-u'2‖∞＜ε.

現(xiàn)證(i)成立.若h2≥0,h2?0,則u2(t)≥‖u2‖∞t,t∈[0,1](見文獻(xiàn)[7]的Lemmma 3.4和文獻(xiàn)[11]的Lemma 2.2).由上述的證明可知,|u'1(t)-u'2(t)|＜ε,?t∈[0,1].因?yàn)閡1(0)=u2(0)=0,利用中值定理得u1(t)≥u2(t)-εt,t∈[0,1].令ε＜ε0‖u2‖∞,則u1(t)≥(1-ε0)u2(t).故~u1(t)≥(1-ε0)~u2(t),t∈[0,1].

現(xiàn)證(ii)成立.由引理3可知,當(dāng)1＜p＜2時(shí),

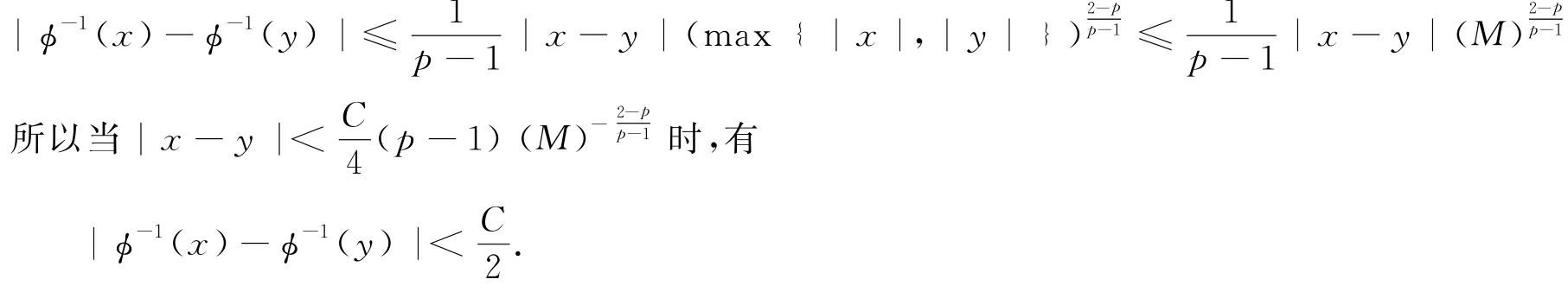
由引理3可知,當(dāng)p≥2時(shí),|?-1(x)-?-1(y)|≤2?-1(|x-y|).

引理7 若存在常數(shù)λ～＞0,使得λ＞λ～,則存在常數(shù)C0＞0,使得(2)的任何一個(gè)正解u(t)滿足

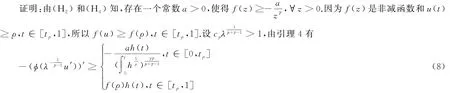
將(8)式的不等號(hào)的右邊定義為h1,由引理6得,h1∈L1(0,1).令w∈C1[0,1]滿足

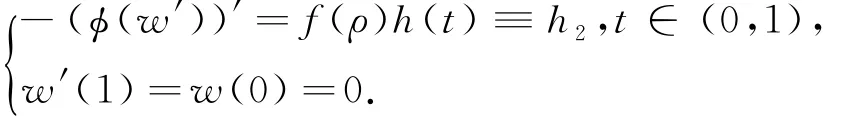
則w(t)≥ ‖w‖∞t,t∈[0,1](見文獻(xiàn)[7]的Lemmma 3.4和文獻(xiàn)[11]的Lemma 2.2).因?yàn)樗援?dāng)λ足夠大時(shí),有

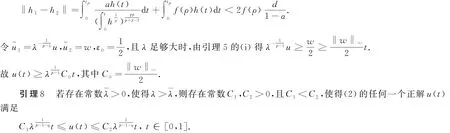
證明：令ε∈(0,1),由(H5)知,存在一個(gè)常數(shù)m＞0,使得

(L-ε)zq≤f(z)≤ (L+ε)zq,z＞m.

若λ＞λ～,由引理7知,u(t)≥.令dλ是使得u(t)≥dλt成立的最大常數(shù).

因?yàn)棣铡荨铡辴(見文獻(xiàn)[7]的Lemmma 3.4和文獻(xiàn)[11]的Lemma 2.2),所以

2 主要結(jié)果的證明

為了利用上述引理7～9,我們假設(shè)λ＞1是足夠大的數(shù).

定理1的證明：令u,v是問題(2)的兩個(gè)正解,由引理8知,

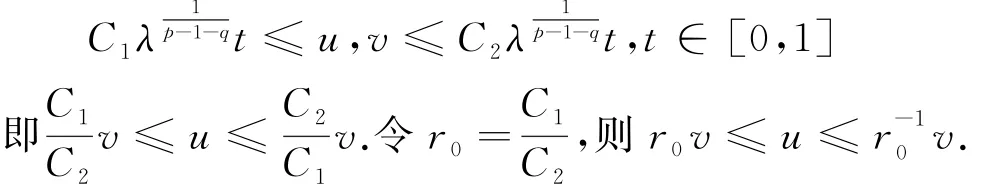
令r1是使得r1v≤u≤r-11v成立的最大常數(shù),并且我們假設(shè)r1＜1.

因此

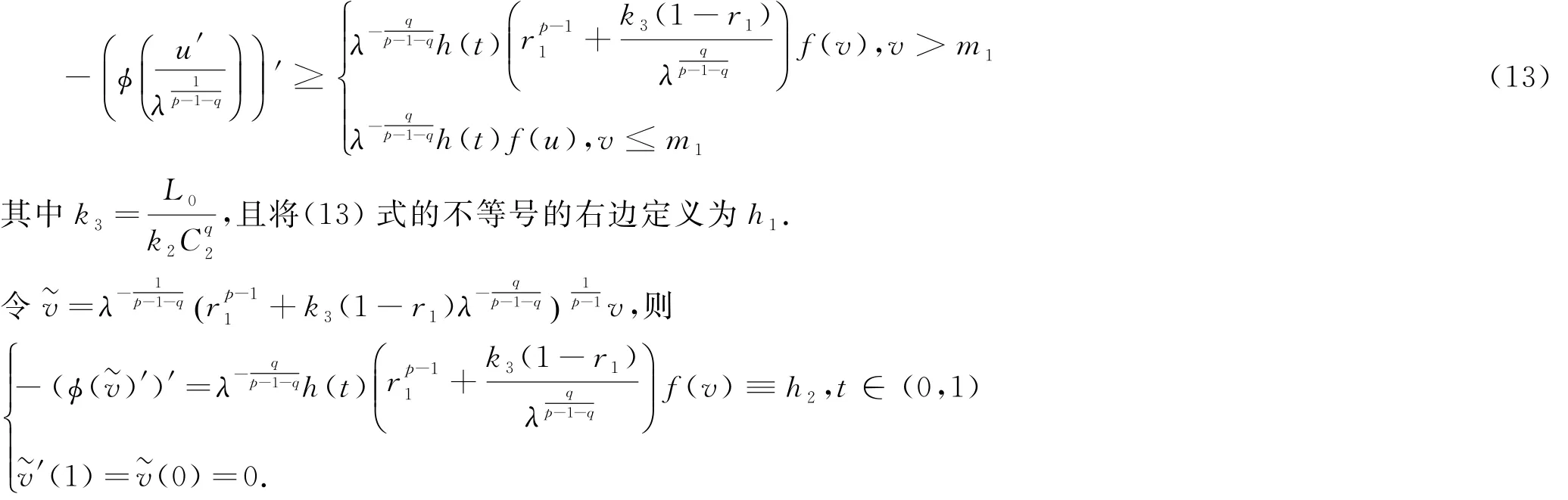
由(12)式知,hi∈L1(0,1),i=1,2.所以有

其中k4＞0是一個(gè)與r0,k3和p有關(guān)的常數(shù).因?yàn)棣恕迺r(shí),‖h1-h2‖→0,所以當(dāng)λ足夠大時(shí),我們有

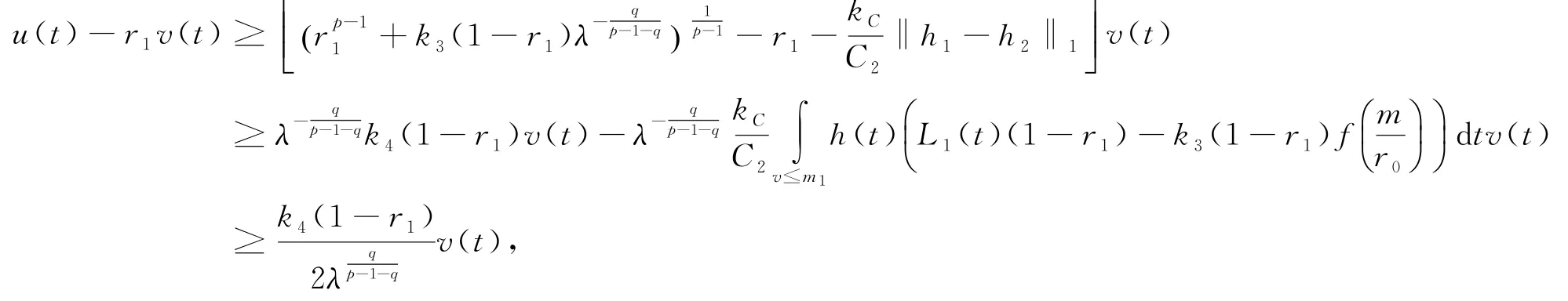
所以存在一個(gè)實(shí)數(shù)r2＞0,使得

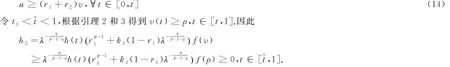
所以

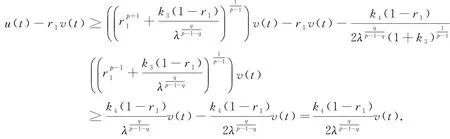
因此,存在一個(gè)實(shí)數(shù)r3＞0,使得

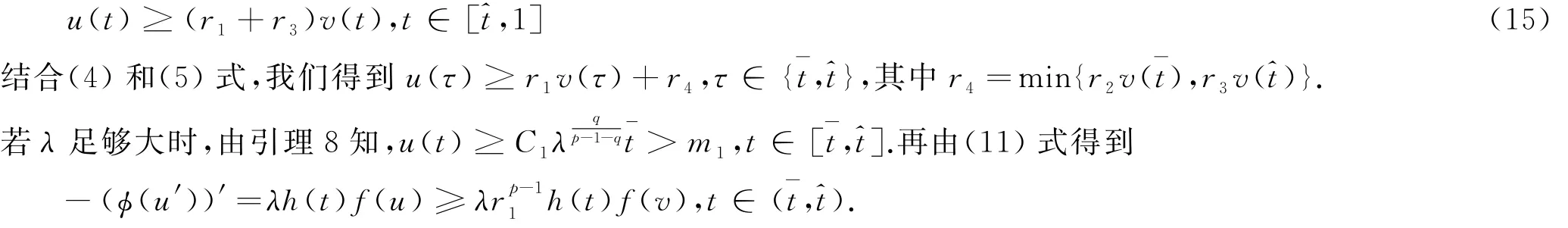
又因?yàn)?/p>

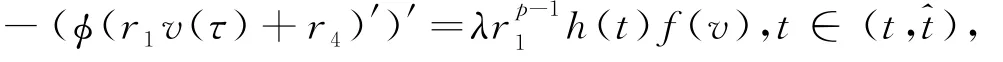
且u(τ)≥r1v(τ)+r4,τ∈ (t^,t).因此,利用弱比較原理(見文獻(xiàn)[10]的Lemma A.2)得到

結(jié)合(14)～(16)式得到,存在一個(gè)實(shí)數(shù)r5＞0,使得u(t)≥(r1+r4)v(t),t∈[0,1].類似地,也可以得到存在一個(gè)實(shí)數(shù)r6＞0,使得v(t)≥(r1+r6)u(t),t∈[0,1].因此,存在一個(gè)實(shí)數(shù)r～＞0,使得(r1+r～)v(t)≤u(t)≤(r1+r～)-1v(t),t∈[0,1].這與r1是使得r1v≤u≤r1-1v成立的最大常數(shù)矛盾,所以r1≥1.這意味著u=v,t∈[0,1].