李宇芳,姚維利

(上海大學(xué)理學(xué)院,上海200444)

1 引言及主要結(jié)論

上式描述了素?cái)?shù)的大致分布情況,被稱為素?cái)?shù)定理.該定理是整個數(shù)論中的核心結(jié)果之一,在數(shù)論中起到了奠基作用,也有很多種等價形式[1],在很多領(lǐng)域都非常有應(yīng)用價值[2].例如:在數(shù)學(xué)方面,可以估計(jì)隨機(jī)取得的整數(shù)n是素?cái)?shù)的概率為1/logx;在計(jì)算科學(xué)方面,是試除法中檢驗(yàn)一個數(shù)是否為素?cái)?shù)的關(guān)鍵計(jì)算步驟之一;在密碼學(xué)方面,1978年,麻省理工學(xué)院(Massachusetts Institute of Technology,MIT)3個計(jì)算機(jī)科學(xué)家Rivest,Shamir和Adleman提出了第一個實(shí)用公鑰密碼——RSA密碼體制.該密碼體制就是基于素性檢測和整數(shù)分解,其安全性依賴于大整數(shù)素?cái)?shù)分解問題的困難性.

記ω(n)是正整數(shù)n的不同素因子的個數(shù),特別地,ω(1)=0.令

定義

式(1)被稱為廣義的素?cái)?shù)分布函數(shù),因此很多數(shù)論學(xué)者對其進(jìn)行了研究.比如,在1909年,Landau[3]首先證明了對k≥1有

之后,Sathe[4]和Selberg[5]改進(jìn)了這個結(jié)果,得到當(dāng)1≤k≤C loglogx時,

這里

目前,較好的結(jié)果是由Hildebrand等[6]提出的,即存在常數(shù)ρ,δ使得當(dāng)

其中

1859年,黎曼提出如下猜想:ζ(s)的非顯然零點(diǎn)都落在臨界線Res=1/2上,即著名的黎曼猜想,其在數(shù)論中有著舉足輕重的地位.

本工作主要研究具有固定素因子個數(shù)的整數(shù)分布情況,探討了黎曼猜想對其漸近式中誤差項(xiàng)的影響.為了方便表達(dá),引入如下記號,設(shè)s=σ+it,0＜ε＜1/logx,

定理1 在黎曼猜想下,設(shè)C為正常數(shù),當(dāng)x≥3,1≤k≤C loglogx時,有

其中

注1:由文獻(xiàn)[4-5],有

其中

因此,本工作重點(diǎn)是得到式(2)中誤差項(xiàng)的估計(jì).

注2:應(yīng)用黎曼猜想,素?cái)?shù)定理可加強(qiáng)[7-8]為

2 預(yù)備知識

為了定理的證明,下面給出以下3個引理作為預(yù)備知識.

絕對收斂.

證明 參見文獻(xiàn)[9].

引理2 由文獻(xiàn)[10]中的定理11.7,假設(shè)∑f(n)n-s對σ＞σa絕對收斂,如果f是積性函數(shù),則有

引理 3 (Perron公式)設(shè)x≥2,記‖x‖為x和離其最近整數(shù)之間的距離,則當(dāng)b＞σa,T ≥ 2有

證明 參見文獻(xiàn)[7]中的定理1.

3 定理的證明

下面給出定理的證明.由fk(n)的定義和留數(shù)定理有

其中r＞0為常數(shù).上式兩邊對n求和,得到

因?yàn)閦ω(n)為積性函數(shù),所以由引理2可知,當(dāng)Re s＞1時,

根據(jù)引理3,式(3)中的和式可表示成

其中

為了估算式(4)中的余項(xiàng),取

由于|z|=r,所以

因此式(4)第一個余項(xiàng)

因?yàn)?/p>

由Euler積分公式可知

所以式(4)第二個余項(xiàng)

根據(jù)式(5),式(4)最后一個余項(xiàng)

綜上可得,

所以式(4)可化簡為

由于

由于

根據(jù)黎曼猜想,ζ(s)的非顯然零點(diǎn)都落在臨界線Re s=1/2上,s=1為唯一的極點(diǎn).所以可以利用留數(shù)定理建立圍道,將式(7)主項(xiàng)的積分區(qū)間轉(zhuǎn)化到C-3∪C-2∪C-1∪C0∪C1∪C2∪C3上,即

其中

不難看出,在C-1∪C0∪C1上的積分可取為主項(xiàng),其余為余項(xiàng)(見圖1).

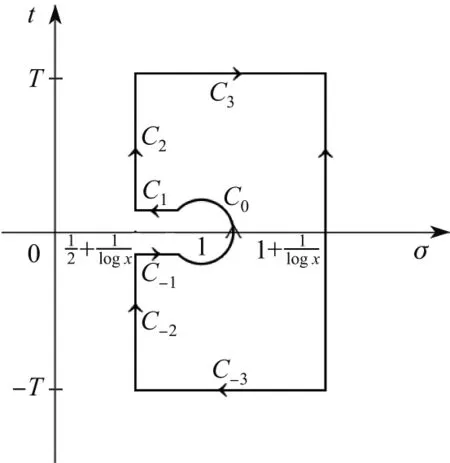
圖1 圍道Fig.1 Contour

接下來,首先計(jì)算C3∪C-3部分的積分.根據(jù)文獻(xiàn)[11]中的定理4.2,

因?yàn)?/p>

因此

下面估算C2∪C-2部分的積分,因?yàn)閷≥2,參考文獻(xiàn)[2],有

所以

由此

所以

下面考慮C2∪C-2中0＜t＜2的情況.當(dāng)0＜t＜2時,由ζ(s)的定義和其解析性可知,ζ(s)有界.根據(jù)文獻(xiàn)[12]中的注1.5.3,ζ(s)在0＜ t＜ 2內(nèi)沒有零點(diǎn),所以必然有界.由式(10)及以上說明可知,

綜上,根據(jù)式(7),(9),(11)可得

將式(12)代回式(3)可得

由于式(5)及

式(13)中的誤差項(xiàng)

綜上,

其中

定理1證明完畢.