ONE-DIMENSIONAL VISCOUS RADIATIVE GAS WITH TEMPERATURE DEPENDENT VISCOSITY?
Lin HE(何躪)
Institute of Applied Mathematics,Academy of Mathematics and System Science The Chinese Academy of Sciences,Beijing 100190,China
E-mail:helin19891021@163.com
Yongkai LIAO(廖勇凱)? Tao WANG(王濤)Huijiang ZHAO(趙會江)
School of Mathematics and Statistics,Wuhan University,Wuhan 430072,China
Hubei Key Laboratory of Computational Science,Wuhan University,Wuhan 430072,China
E-mail:yongkai.liao@whu.edu.cn;tao.wang@whu.edu.cn;hhjjzhao@hotmail.com
Abstract This paper is concerned with the construction of global,large amplitude solutions to the Cauchy problem of the one-dimensional compressible Navier–Stokes system for a viscous radiative gas when the viscosity and heat conductivity coefficients depend on both speci fic volume and absolute temperature.The data are assumed to be without vacuum,mass concentrations,or vanishing temperatures,and the same is shown to be hold for the global solution constructed.The proof is based on some detailed analysis on uniform positive lower and upper bounds of the speci fic volume and absolute temperature.
Key words compressible Navier–Stokes system;temperature-dependent viscosity;viscous radiative gas;global solution;asymptotic behavior
1 Introduction
The dynamics of one-dimensional compressible viscous and heat-conducting flow can be described in the Lagrangian coordinates by the compressible Navier–Stokes system:
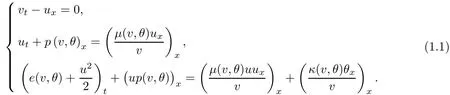
Here t>0 and x∈R are the time and Lagrangian spatial variables,respectively.The speci fic volume v,velocity u,and absolute temperature θ are unknown functions of t and x.The pressure p,internal energy e,viscosity coefficientμ >0,and heat conductivity coefficient κ >0 are prescribed through constitutive relations as functions of v and θ.The thermodynamic variables are related through Gibbs’equation de= θds?pdv with s being the speci fic entropy.
This paper concerns system(1.1)with prescribed initial data
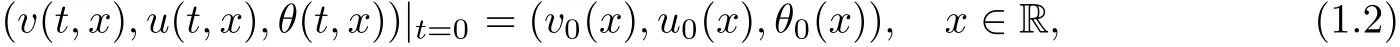
which are assumed to satisfy the far- field condition:
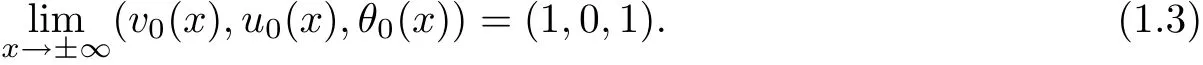
Our main purpose is devoted to the construction of global,smooth,large amplitude,non-vacuum solution(v(t,x),u(t,x),θ(t,x))to Cauchy problem(1.1)–(1.3)with temperaturedependent transport coefficientsμ and κ when the thermodynamic variables v,p,e,θ,and s do not satisfy the equations of state for ideal polytropic gases.In fact,our choice of constitutive relations are motivated by the following system describing the motion of compressible radiative and reactive gas:
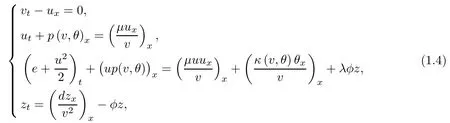
where z=z(t,x)represents the reactant mass fraction.The positive constants d and λ are the species di ff usion coefficient and the di ff erence in the heat between the reactant and the product,respectively.The reaction rate function φ = φ(θ)is de fined by the first-order Arrhenius law(cf.[11]):

where positive constants K and A are the coefficients of the rate of the reactant and the activation energy,respectively,and β is a non-negative number.
When the radiation is treated as a continuous field and both the wave and photonic e ff ect are considered,the high-temperature radiation is at thermal equilibrium with the fluid.Then pressure p consists of a linear term in θ corresponding to the perfect polytropic contribution and a fourth-order radiative part due to the Stefan–Boltzmann radiative law(see[36]for instance)so that
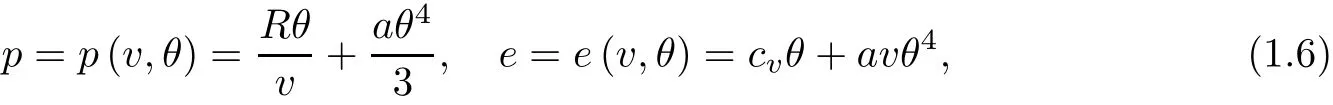
where positive constants R,cv,and a are the perfect gas constant,the speci fic heat,and the Stefan–Boltzmann constant,respectively.
Since the energy producing process inside the medium is taken into account in system(1.4),where the gas consists of a reacting mixture and the combustion process is current at the high temperature stage,the experimental results for gases at high temperatures in[54]show that both μ and κ may depend on the speci fic volume v and/or the absolute temperature θ.In this paper,we focus on the case when the heat conductivity κ takes the following form(cf.[7])

for some positive constants κ1,κ2,and b.As for the viscosity coefficient μ,motivated by the work[52]for the one-dimensional viscous,heat-conducting ideal polytropic gas,we assume that
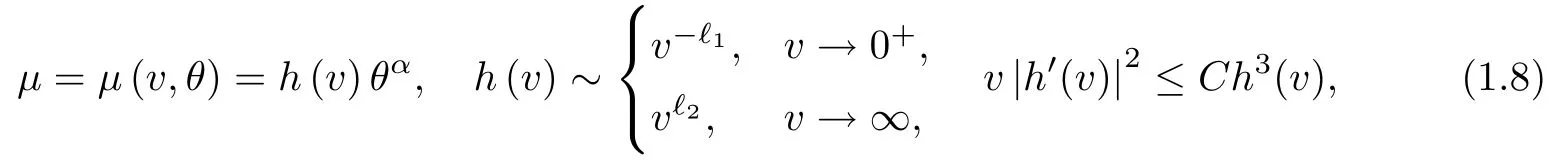
where h(v)is a smooth function of v for v>0,and α, ?1, ?2,and C are positive constants.Here and in the rest of this paper,f(x)~g(x)(x→x0)means that there exists a constant C ≥ 1 such that C?1g(x)≤ f(x)≤Cg(x)holds in a neighborhood of x0.
Before stating our main result,it is worth to pointing out that the study on the global solvability and large time behaviorsof the global solutions to the initial value problem and/or the initial-boundary value problems of the one-dimensional compressible Navier–Stokes equations(1.1)is one of the hottest topics in the field of nonlinear partial di ff erential equations and many results have been obtained up to now.To go to the theme of this paper,we will only review some results on the compressible Navier–Stokes type equations(1.4)–(1.7)describing the motion of compressible radiative and reactive gas as follows:
When the viscosity coefficientμis a positive constant,the results obtained can be summarized as in the following.
For the initial-boundary value problem of(1.4)–(1.7)in the bounded interval(0,1)with the free boundary conditions

on the stress σ(t,x)and homogeneous Neumann condition
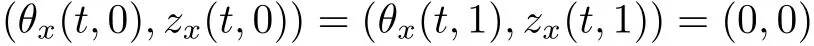
on both θ(t,x)and z(t,x),Umehara–Tani[46]proved the global existence,uniqueness of a classical solutions under the assumptions 4≤b≤16 and 0≤β≤13/2.Later on,they improved the results in[47]to the case of b ≥ 3 and 0 ≤ β See also the result by Jiang–Zheng[17]for more general assumptions on κ; For the initial-boundary value problem of(1.4)–(1.7)in(0,1)with homogeneous Dirichlet boundary condition u(t,0)=u(t,1)=0 and homogeneous Neumann condition on θ(t,x)and z(t,x),Documet[7]established the global existence and exponential decay in H1(0,1)of solutions for b ≥ 4 and β >0.Recently,Jiang–Zheng[18]improved this result to the case of b≥ 2 and 0≤ β For the Cauchy problem of(1.4)–(1.7),results on the global solvability and the precise description of large time behavior of the global solution constructed were established very recently by Liao–Zhao in[33]for b>11/3 and 0≤ β For sphericallty symmetric motions of compressible radiative and reactive gases,the global existence,uniqueness and exponential stability of spherically symmetric solutions in the bounded annular domain ? ={x ∈ Rn:0 For the case when the viscosity coefficientμis a smooth,possible degenerate function of the speci fic volume v for positive v,the two types of initial-boundary value problems of(1.4)–(1.7)in the bounded interval(0,1)mentioned above were studied in[31,32],while the Cauchy problem was treated in Liao–Xu–Zhao[30].It is worth to pointing out that all the estimates obtained in[30–32]depend on the time variable t,and thus the problem on the large time behavior of global solutions constructed in[30–32]remains unsolved. Even so,to the best of our knowledge,no result is available for the case when the viscosity coefficientμdepends on the absolute temperature up to now.As pointed out before,since the physical phenomena described by system(1.4)involve high temperature process and the experimental results for gases at high temperatures in[54]show that the viscosity coefficientμ may also depend on the speci fic volume v and/or the absolute temperature θ,a natural and interesting question is:Whether can we obtain a global solvability result for the Cauchy problem(1.4)–(1.7)with large initial data or not for a class of density and temperature dependent viscosity coefficientμsatisfying(1.8)?The main goal of this paper is devoted to such a problem.Since the appearance of the reaction equation,i.e.,the fourth one in(1.4),does not cause any essential difficulty in our analysis,we will focus on the Cauchy problem of(1.1),(1.6)–(1.8)with prescribed large initial data(1.2)satisfying the far field condition(1.3)in the rest of this paper. Now we are in a position to state our main result.To do so,for each given positive constant 0 and then our result can be stated as follows. Theorem 1.1Suppose that (i)The viscosity coefficientμsatis fies(1.8); (ii)The parameters b,?1,and ?2are assumed to satisfy: where Π0and V0≤ 1 are given positive constants.Then there exists ?0>0,which depends only on Π0,V0and H(C0),such that if the Cauchy problem(1.1)–(1.3),(1.6)–(1.8)admits a unique solution(v(t,x),u(t,x), θ(t,x))satisfying Remark 1.2Several remarks concerning our main result are listed below: (i)It is easy to see that for each b ≥ 7,one can easily find ?1>1 and ?2>1 sufficiently large such that the assumption(1.11)holds.Since our main purpose is to show that we can indeed obtain a global solvability result for the Cauchy problem(1.1)–(1.3),(1.6)–(1.7)for a class of density and temperature dependent viscosityμwhich satis fies(1.8),assumptions(1.10)and(1.11)that we imposed on the parameters b, ?1,and ?2are far from being optimal; (ii)If we take α=0,then our main result Theorem 1.1 tells us that one can obtain a result on the global solvability together with the precise description of the large time behaviors of solutions to the Cauchy problem(1.1)–(1.3),(1.6)–(1.7)for a class of density dependent viscosityμwhich satis fies Here C>0, ?1and ?2are some positive constants satisfying(1.10)and(1.11).Recall that for the case when the viscosity coefficientμis a degenerate function of v(cf.μ=v?α,α ∈ [1/3,1/2)),although a global solvability result is obtained in[30],we do not know how to deduce the desired large time behaviors of the global solutions constructed there due to the lack of uniform-in-time estimates.We note,however,that our main result,i.e.,Theorem 1.1,yields the large time behaviors of the global solutions for a class of nondegenerate density dependent viscosity coefficientμ. Now we outline the main difficulties encountered in the proof of Theorem 1.1.As is well known,the key point to deduce the global solvability result of the Cauchy problem(1.1)–(1.3),(1.6)–(1.8)is to derive the desired positive lower and upper bounds on the speci fic volume v(t,x)and the absolute temperature θ(t,x). For the case when the viscosity coefficientμis a positive constant,motivated by the work of Jiang[19–21]for the viscous,heat-conducting ideal polytropic gas,Liao–Zhao[33]have used the following cut-o fffunction By virtue of(1.14),one can deduce the uniform-in-time positive lower and upper bound of v(t,x). As for the uniform positive lower and upper estimate on θ(t,x),motivated by the work of[25]for the initial-boundary value problem of the one-dimensional compressible Navier–Stokes equation in bounded interval for general gas,the following auxiliary functions are introduced in[33]to derive the uniform upper bound of the absolute temperature θ(t,x).It is worth to emphasizing that the argument used in[33]to deduce the desired upper bound estimate on θ(t,x)relies highly on the uniform bounds on v(t,x)obtained before. When the viscosity coefficientμis not a positive constant but depends only on the speci fic volume v,the above argument can not be used any longer.In fact,for such case we can not deduce a similar explicit repression for v(t,x)and consequently we can not deduce the desired positive lower and upper bounds on v(t,x) first.The main ideas used in[30]are the following: (i)Based on the following identity which is observed first by Kanel’in[24]for isentropic viscous flow,one can deduce an estimate on the lower and upper bounds of the speci fic volume v in terms ofby employing Kanel’s argument provided that μ satis fies suitable growth conditions as v→0+and v→+∞;(ii)Noticing that h(t,x)=1/θ(t,x)satis fies one can employ the standard maximum principle to yield an estimate on the lower bound of the absolute temperature in terms of (iii)By utilizing the argument used in[44]and[4,25,33],one can then deduce an estimate onFrom which and the estimates on the lower and upper bounds on v(t,x),the lower estimate on θ(t,x),one can then deduce the desired positive lower and upper estimates on both v(t,x)and θ(t,x)provided that the parameter b appearing in(1.7)and growth rates of the viscosity coefficientμas v→0+and v→+∞satisfy certain conditions and then the desired global solvability result follows immediately. For the case considered in this paper,the viscosity coefficientμdepends on both the speci fic volume v and the absolute temperature θ.For such a case,the identity corresponding to(1.15)becomes Since the last term in(1.18)is a highly nonlinear term,the temperature dependence of the viscosityμhas a strong in fluence on the solution and leads to difficulties in mathematical analysis for global solvability with large data,and as pointed out in[16],such a dependence has turned out to be especially problematic and challenging. A natural way to go on is to use certain smallness mechanism induced by the structure of the system to control the last term in(1.18)suitably.It was to do so that we need to ask the viscosity coefficientμ to take the form(1.8)and our main idea is to the smallness of|α|to control the last highly nonlinear term in(1.18).We note,however,that to close the analysis,or in other words to determine the upper bound of|α|in terms of the initial data,one had to deduce the uniform positive lower and upper bounds on the absolute temperature θ which are independent of the time variable t.It is worth to pointing out that such a problem is considered by Wang–Zhao in[52]for the one-dimensional,compressible Navier–Stokes system for a viscous and heat conducting ideal polytropic gas for a class of density and temperature dependent viscosity coefficientμsatisfying(1.8).We recall,however,that the argument of Wang–Zhao in[52]is first to use Kanel’s method[24]to obtain the lower and the upper bound of v(t,x)in terms of(see Lemma 2.3 in[52]),then to employ the technique used in Li–Liang in[27]to derive the uniform upper bound of θ(t,x).Note that the method used by Wang–Zhao in[52]to deduce the uniform upper bound of θ(t,x)relies on the following Sobolev inequality(see also(2.72)in Wang–Zhao[52])For our problemis bounded due to Lemma 2.1,but the method employed in[52]to deduce the estimate onloses its power in our case which is caused by the fourthorder radiative part in both p(v,θ)and e(v,θ),cf.(1.6);Besides,one can see the assumptionμ = κ also plays an important role in the process of deriving the upper bound of θ(t,x)in their discussion.Thus the story is di ff erent sinceμ6=κ in our case. To overcome the above difficulties,we introduce some new auxiliary functions X(t),W(t),Z(t)and W(t)(see(3.1)in section 3)to deduce the uniform-in-time upper bound of θ(t,x).More precisely,our strategy to prove Theorem 1.1 can be stated as follows: (i)We first apply Kanel’s method[24]to deduce the lower and the upper bounds of v(t,x)in terms ofsimultaneously in Lemma 2.3.Notice that the assumption(1.10)plays an important role in our discussion.To control the last term in(1.18),we will use the smallness of|α|; (ii)Due to(3.12)and(3.13),we introduce the auxiliary functions X(t),Y(t),Z(t)and W(t)(see(3.1))to deduce the upper bound of θ(t,x)in Lemmas 3.1–3.4.Thus the lower and the upper bound of v(t,x)follows from Lemma 2.3.We should emphasize that all the bounds obtained above are independent of the time variable t;We then adopt the method in Liao–Zhao[33]to deduce the positive local-in-time lower bound of θ(t,x)and notice that such a bound depends on the time variable t; (iii)By using the dedicated energy method,we can derive energy type estimates of higherorder derivatives in Section 4 and Section 5;Then by using the continuation argument designed in Wang–Zhao[52],we can then prove Theorem 1.1. Before concluding this section,we recall that there are also many results on the construction of global,smooth,large amplitude,non-vacuum solutions and on the precise description of the large time behaviors of the global solutions constructed to compressible Navier–Stokes system for a viscous and heat conducting ideal polytropic gas,cf.[1–3,16,26,40]for the one-dimensional initial-boundary value problem in bounded interval,[1,6,12–15,20–22,27,34,38,39,41,44,45,50–53]for the corresponding one-dimensional problem in unbounded domain and[19,28,37,48,49]for global symmetric flows of multi-dimensional compressible Navier–Stokes equations.For compressible Navier–Stokes equations with general constitutive relations and other related compressible Navier–Stokes type equations,see[4,25,35,55]and the references therein. The rest of the paper is organized as follows.We derive pointwise bounds on the speci fic volume in Section 2.Then pointwise bounds on the absolute temperature will be derived in Section 3.Some second-order and third-order energy type estimates and the proof of our main result will be given in Section 4 and Section 5,respectively. NotationsThroughout this paper,C ≥ 1 or Ci≥ 1(i=1,2,···)is used to denote a generic positive constant which may depend only on Π0,V0and H(V0),where Π0,V0and H are given by(1.12),(1.13)and(1.9),respectively.Note that these constants may vary from line to line.C(·,·)stands for some generic constant depending only on the quantities listed in the parenthesis.?<1 represents some small positive constant. For function spaces,Lq(R)(1≤q≤∞)denotes the usual Lebesgue space on R with norm k ·kLq(R),while Hq(R)denotes the usual Sobolev space in the L2sense with norm k·kHq(R).We denote by C(I;Hq(R))the space of continuous functions on the internal I with values in Hq(R)and L2(I;Hq(R))stands for the space of L2-functions on I with values in Hq(R).For simplicity,we use k·k∞to denote the norm in L∞([0,T]×R)with T>0 being some given positive constant,k·k and k·kqare used to denote the norm k·kL2(R)and the norm k·kHq(R),respecitively. Finally,A.B(or B&A)means that A≤CB holds uniformly for some generic positive constant C. We de fine the set Since the existence and uniqueness of solution(v(t,x),u(t,x),θ(t,x))to the Cauchy problem(1.1)–(1.3)with constitutive relations(1.6),(1.7)and(1.8)in the set of functions X(0,t1;m1,m2,N)for some sufficiently small t1>0 and certain positive constants m1,m2and N is guaranteed by the well-established local existence result for hyperbolic-parabolic system,cf.[23],suppose that the local solution(v(t,x),u(t,x),θ(t,x))to the Cauchy problem(1.1)–(1.3)with constitutive relations(1.6)–(1.8)has been extended to the time step t=T for some positive constant T>0 and(v(t,x),u(t,x),θ(t,x)) ∈ X(0,T;m1,m2,N)for some positive constants T,mi≤1(i=1,2)and N≥1,then in order to prove Theorem 1.1,we only need to derive certain a priori estimates on the solution(v(t,x),u(t,x),θ(t,x))in terms of the initial data(v0(x),u0(x),θ0(x))but independent of the constants mi≤ 1(i=1,2)and N ≥ 1. Applying Sobolev’s inequality yields This section is devoted to deducing lower and upper bounds on the speci fic volume v(t,x)in terms of.In the next lemma,we present the basic energy estimate. Lemma 2.1Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have where Proof According to[38],the function η is nothing but the normalized entropy around(v,u,θ)=(1,0,1)for system(1.1),(1.6),(1.7)and(1.8)(see[33]for the derivation). Multiply(1.1)2and(1.1)3with u and(1?θ?1),respectively,add the resulting identities,and use(1.1)1to discover The lemma follows by integrating the above identity over[0,t]×R. The derivation of pointwise bounds for v(t,x)relies on the following lemma. Lemma 2.2Suppose that the conditions listed in Theorem 1.1 hold.Then there is a constant 0< ?1≤ 1,depending only on Π0and V0,such that if Integrating the above identity over[0,t]× R,we obtain from Cauchy’s inequality and(2.2)the following estimate: which combined with(1.8)implies Then(2.5)follows by inserting(2.9)–(2.13)and(2.18)into(2.8). By applying the Kanel′technique(cf.[24]),we obtain pointwise bounds for the speci fic volume v(t,x)in the following lemma. Lemma 2.3 Assume that the conditions listed in Lemma 2.2 hold.Then In view of ?1>1 and ?2>1,we plug(2.5)into(2.22)and utilize Young’s inequality to conclude the estimates(2.19). A direct corollary follows from Lemmas 2.2 and 2.3. Corollary 2.4Assume that the conditions listed in Lemma 2.2 hold.Then for any 0≤t≤T,we have In this section,we will obtain a uniform-in-time upper bound and a local-in-time lower bound for the absolute temperature θ.For this purpose,we set We first employ the basic energy estimate(2.2)to derive the following lemma. Lemma 3.1Assume that the conditions listed in Theorem 1.1 hold,then we can get that Since 2b+6> ?1+2?2,we deduce(3.2)from Young’s inequality.This completes the proof of Lemma 3.1. The next lemma follows directly from Gagliardo–Nirenberg and Sobolev’s inequalities. Lemma 3.2Assume that the conditions listed in Theorem 1.1 hold.Then one can get for each 0≤t≤T that With the above preparations in hand,our next result is to show that X(T)and Y(T)can be controlled by Z(T)and W(T). Lemma 3.3Under the assumptions listed in Theorem 1.1,we have ProofIn the same manner as in[25]an[46],if we set then it is easy to verify that We first rewrite(1.1)3in the following form where the de finition of Hk(4≤k≤9)will be given below. We now turn to control Hk(k=4,5,···,9)term by term.To do so,we can infer from(2.19)that where we have used(1.8),(1.10),(3.8)and Young’s inequality. Next,by virtue of(1.8),(1.10),(2.2)and(3.8),we can conclude As for the term H6,it follows from(1.8),(1.10),(2.2),(2.15)and(3.14)that Now we deal with the term H7.For this purpose,we have by integration by parts that For the first term on the right-hand side of(3.17),it follows from(1.8),(1.10)and(2.19)that It is worth to pointing out that we can deduce from(1.10)and(2.20)that For the last term on the right-hand side of(3.17),one can get that where we have used(1.8),(2.4),(2.19),(3.2),(3.3)and the fact that where we have used(1.1)3,(2.2),(3.2),(3.3),(3.8)and H?lder’s inequality.Consequently,to yield an estimate on H8,it suffices to bound the term.To this end,we can get that where we have used(1.8),(1.10),(2.2),(2.19),(2.20),(3.2),(3.3)and Young’s inequality.Thus we can deduce from(3.25)and(3.26)that As for the term H9,we can deduce from(1.1)3,(2.2),(2.23),(3.8),H?lder’s inequality and the following fact then combining all the above estimates and choosing ?>0 small enough,we can complete the proof of our lemma. Our next result in this section is to show that Z(T)can be bounded by X(T)and Y(T). Lemma 3.4Under the assumptions listed in Theorem 1.1,we have ProofDifferentiating(1.1)2with respect to t and multiplying the resulting identity with ut,we have On the other hand,according to(1.8),we have Thus combining(3.33)–(3.37),we obtain In view of(1.10),one can deduce that Then by virtue of(3.1)and Young’s inequality,we can complete the proof of our lemma. We are in a position to deduce the upper bound of θ(t,x)now.In fact,(3.4),(3.32)and(3.38)tell us that Thus with the hand of Young’s inequality and Lemma 3.3,we can deduce from(3.42)that Finally,choosing ?>0 small enough then using(3.4)and Young’s inequality again,we immediately obtain Recalling the de finition of X(T),Y(T),Z(T)and W(T),then combining Lemmas 2.1–3.4,we have the following lemma. Lemma 3.5Under the assumptions listed in Theorem 1.1,there exist positive constants C1and C2,which depend only on Π0and V0,such that Before concluding this section,let us deduce uniform bounds onandwhich will be used later on.In fact,we have the following lemma. Lemma 3.6Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have Integrating the above identity with respect to t and x over(0,t)×R and taking advantage of(3.41),we arrive at Here we have used(2.2),Lemma 3.5 and Sobolev’s inequality. Moreover,it follows from(2.2),Lemma 3.5 and Cauchy’s inequality that Then combining(3.52)–(3.54)and choosing ?>0 small enough,we can get(3.50). Finally,choosing ?>0 small enough,integrating(3.55)with respect to t over(0,t)and using(2.2)as well as(3.49),we can obtain(3.51). As a result of Lemmas 2.1–3.6,we can obtain the following corollary immediately. Corollary 3.7Under the assumptions listed in Theorem 1.1,there exists a positive constants C3,such that The next estimate is concerned with the local-in-time estimate on the lower bound on the absolute temperature θ(t,x).To this end,we can deduce by repeating the method used in[33]that Lemma 3.8Under the assumptions stated in Theorem 1.1,for each 0≤s≤t≤T and x∈R,there exist a positive constant C4,such that In the following sections,to simplify the presentation,we introduceholds uniformly for some constant Ch,depending only on Π0,V0and H(C2)with C2given in Lemma 3.5.The letter C(m2)will be employed to denote some positive constant which depends only on m2,Π0,V0and H(C2).We note from(1.9)and(3.48)that We estimate the second-order derivatives of(u(t,x),θ(t,x))with respect to the space variable x in the next lemma. Lemma 4.1Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have ProofFirst,di ff erentiating(1.1)2with respect to x,and multiplying the resulting identity by uxxx,we have To estimate the last term in(4.3),we first make some estimate of θα.It follows from(2.4)that Since v(t,x)is bounded,for general smooth function f(v),we have Combining(4.7)and(4.8),we have We plug(4.11),(4.12)and(4.13)into(4.10),and use(4.3)–(4.10)to deduce that Integrating the above identity over[0,t]× R,we obtain from Cauchy’s inequality,(2.4)and(3.48)that Combining(4.14)and(4.19)and taking δ>0 small enough,we can obtain(4.2). ? We next obtain a m2-dependent bound for the second-order derivatives with respect to x of the solution(v(t,x),u(t,x),θ(t,x)). Lemma 4.2Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have ProofDifferentiate(2.7)with respect to x and multiply the result byto find We integrate the above identity over[0,t]× R,and Cauchy’s inequality to obtain On the other hand,one can deduce from(2.14)that In view of(4.4)and Hence applying Cauchy’s inequality yields which combined with(4.2)implies(4.20). Estimates on the third-order derivatives of(v(t,x),u(t,x),θ(t,x))with respect to x will be proved in this subsection.We first give an estimate on the third-order derivatives of u(t,x)and θ(t,x)with respect to x in the following lemma. Lemma 5.1Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have In view of(3.56)and(4.20),we deduce that Next,we di ff erentiate(3.9)with respect to x twice and multiply the result by θxxxxto obtain Combining(5.5)and(5.10)and taking δ>0 small enough,we can obtain(5.1). By using(2.4)and Gronwall’s inequality,we can deduce the m2-dependent bound for the third-order derivatives of(v(t,x),u(t,x),θ(t,x))with respect to x.The proof is similar to that of Lemma 4.2 and hence we omit the details for brevity. Lemma 5.2Under the assumptions listed in Theorem 1.1,for any 0≤t≤T,we have By virtue of Lemma 2.1–Lemma 5.2,we can get the following corollary. Corollary 5.3Under the assumptions listed in Theorem 1.1,there exists a positive constants C(m2)>0 which depends only on m2,Π0,V0and H(C2)with C2being given in Lemma 3.5,such that for all t∈[0,T], With Corollary 5.3 in hand,Theorem 1.1 follows by the combing the well-established local existence of solution(v(t,x),u(t,x),θ(t,x))of the Cauchy problem(1.1)–(1.3)with constitutive relations(1.6),(1.7)and(1.8)which is without vacuum,mass concentrations,or vanishing temperatures,cf.[23],and the continuation argument designed in[52]and we omit the details for brevity.

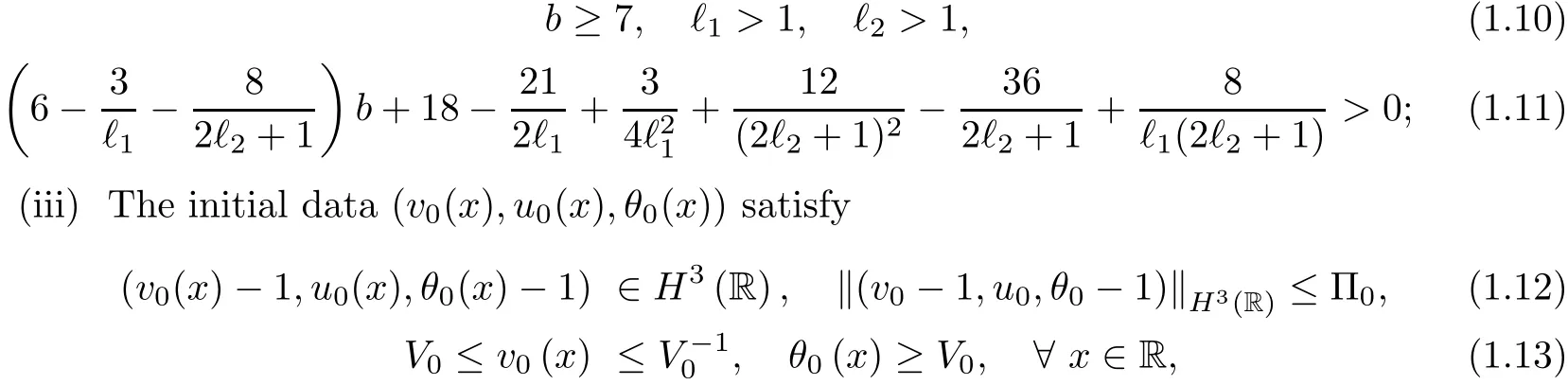

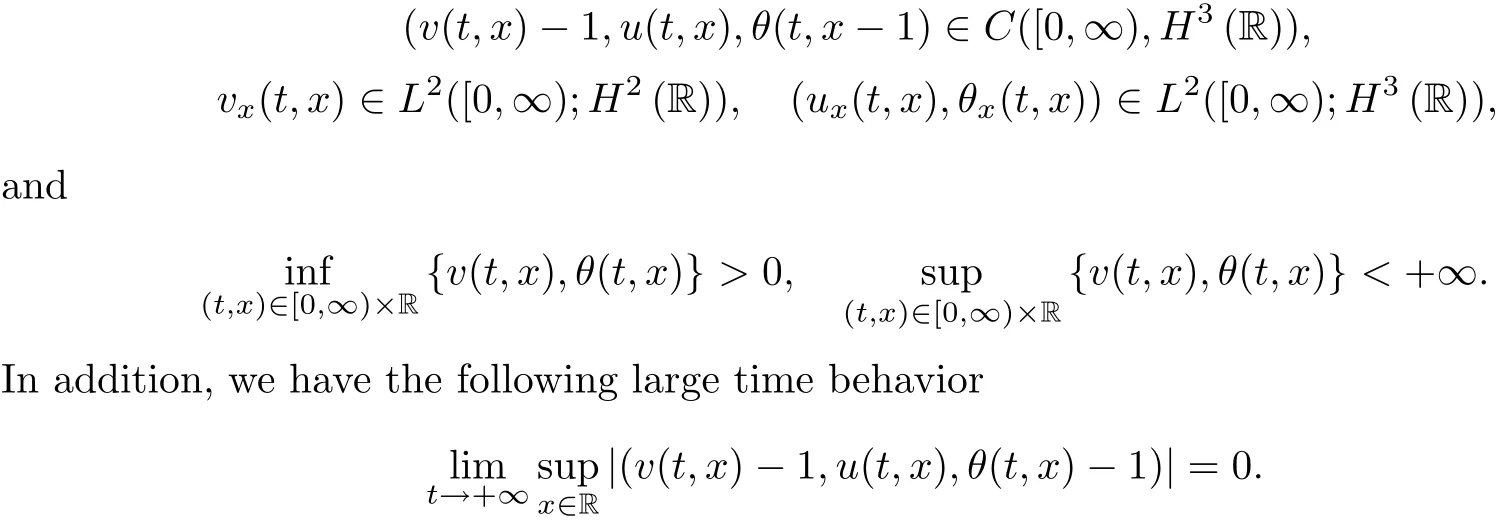
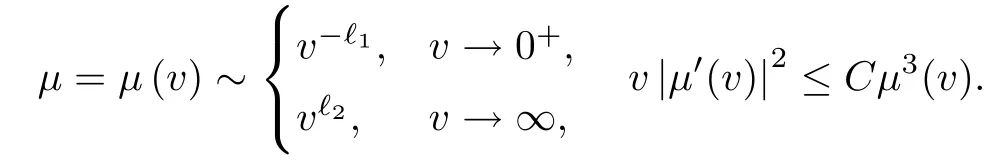
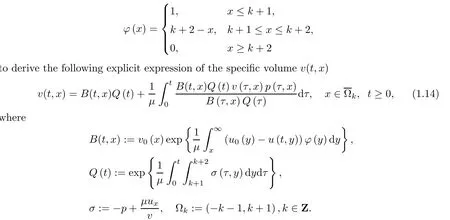


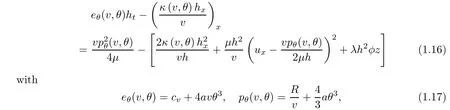


2 Pointwise Bounds for the Speci fic Volume
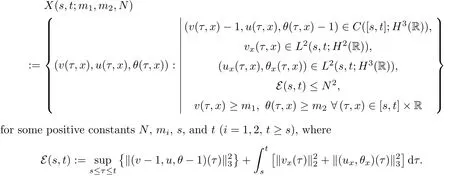
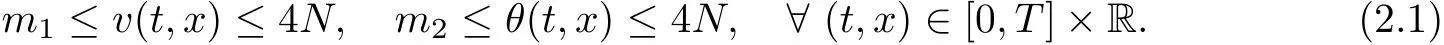
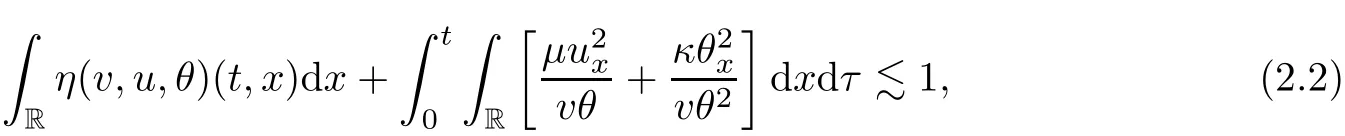
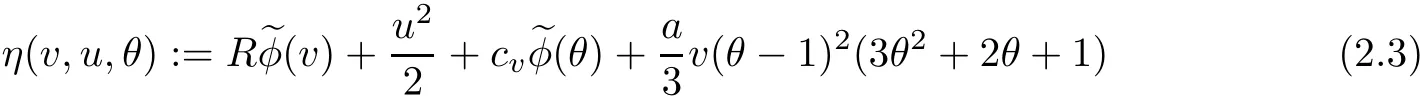
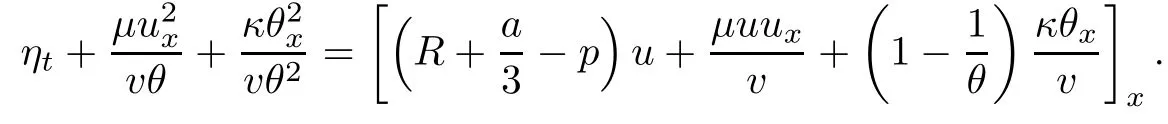

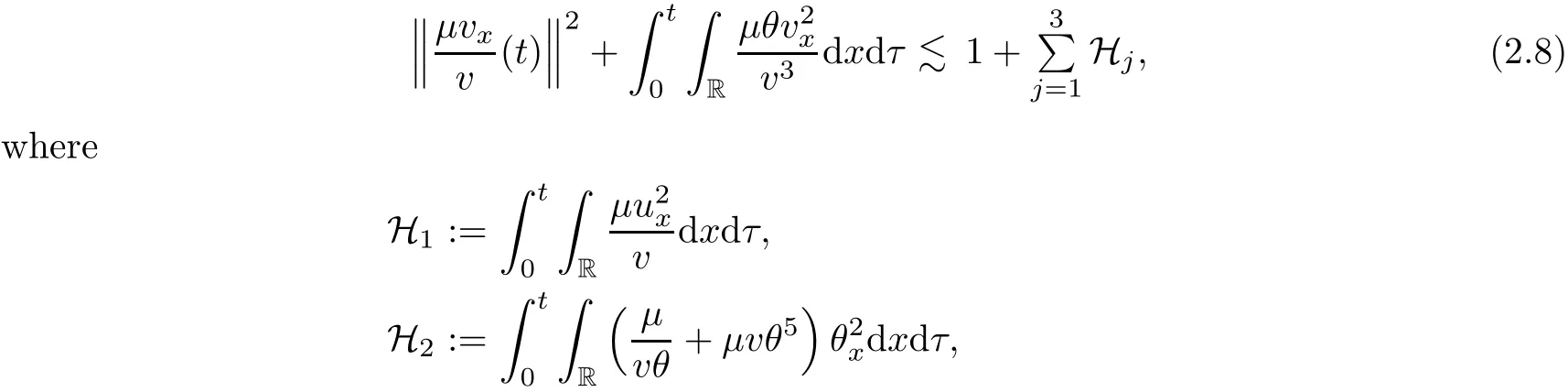


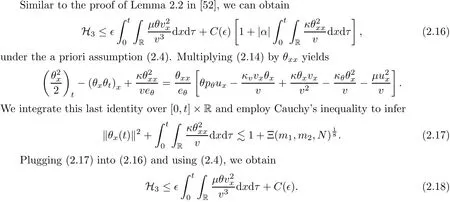


3 Pointwise Bounds for the Absolute Temperature

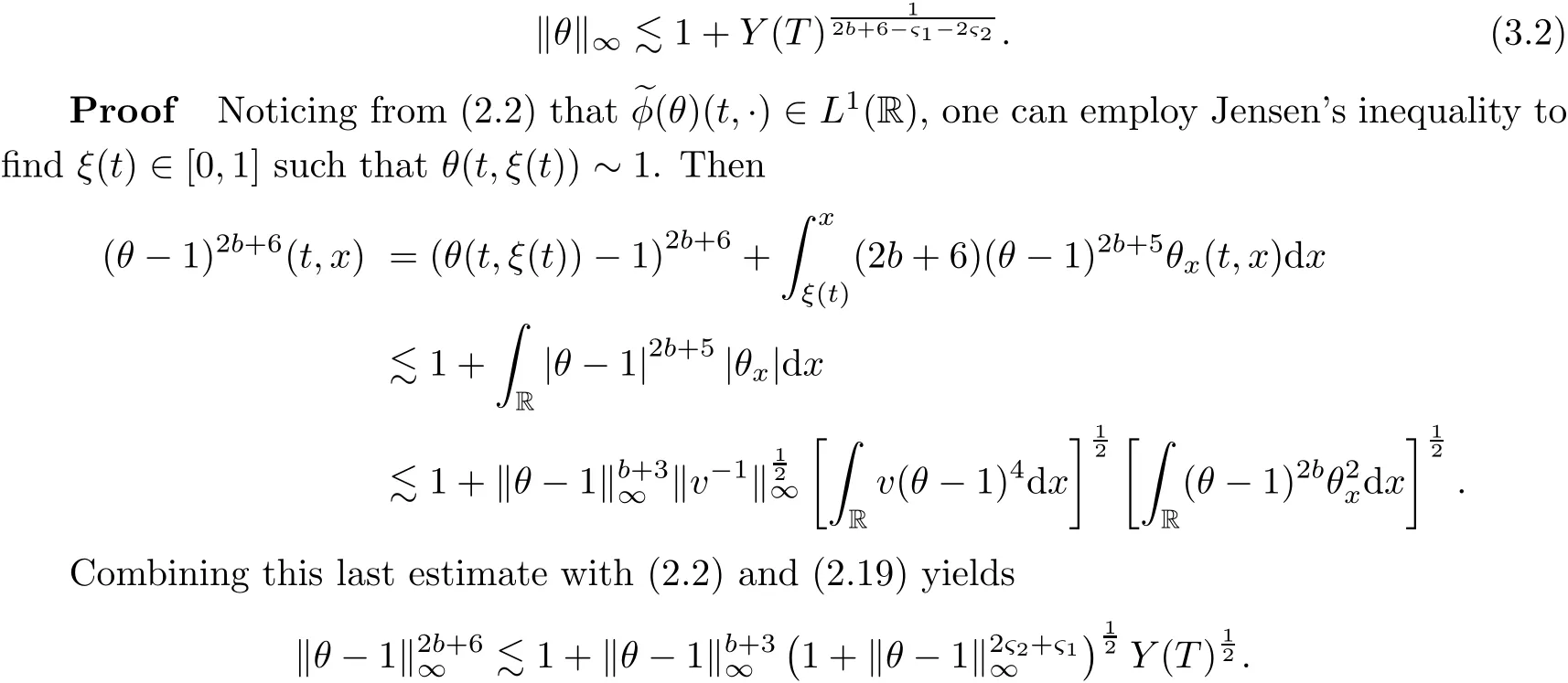

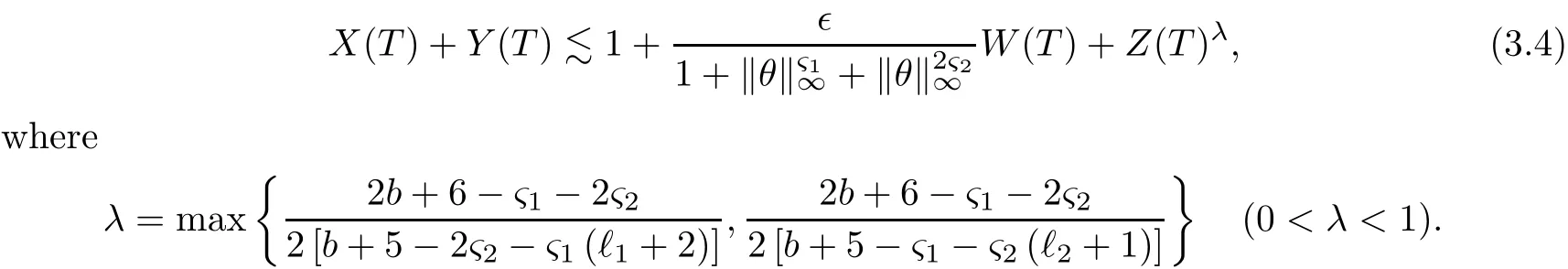

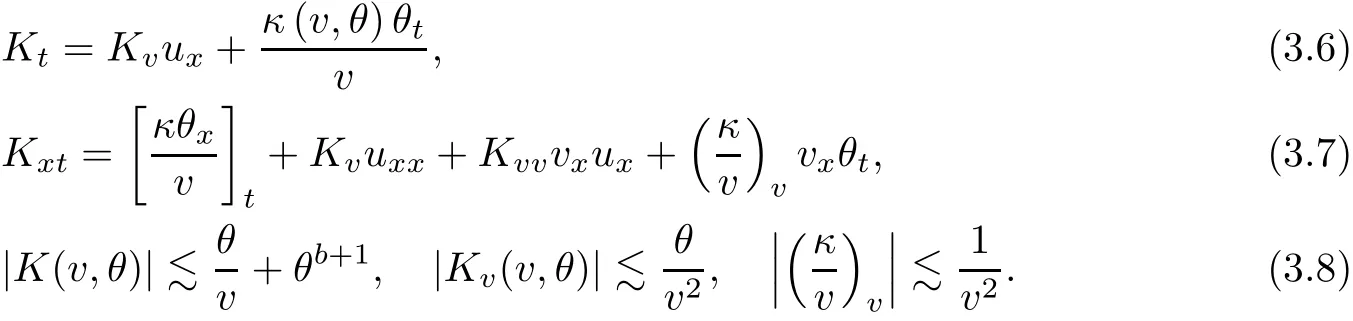

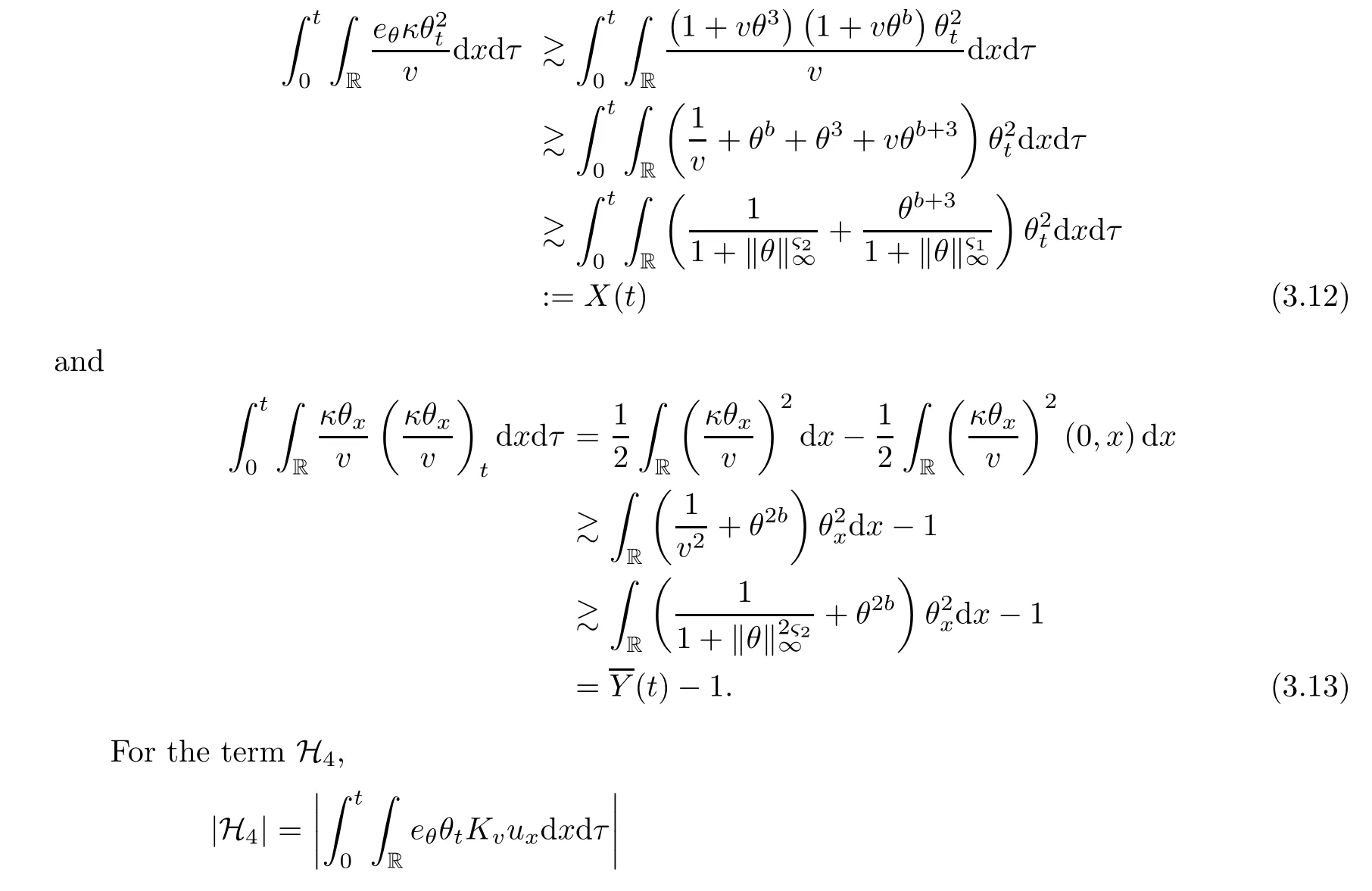
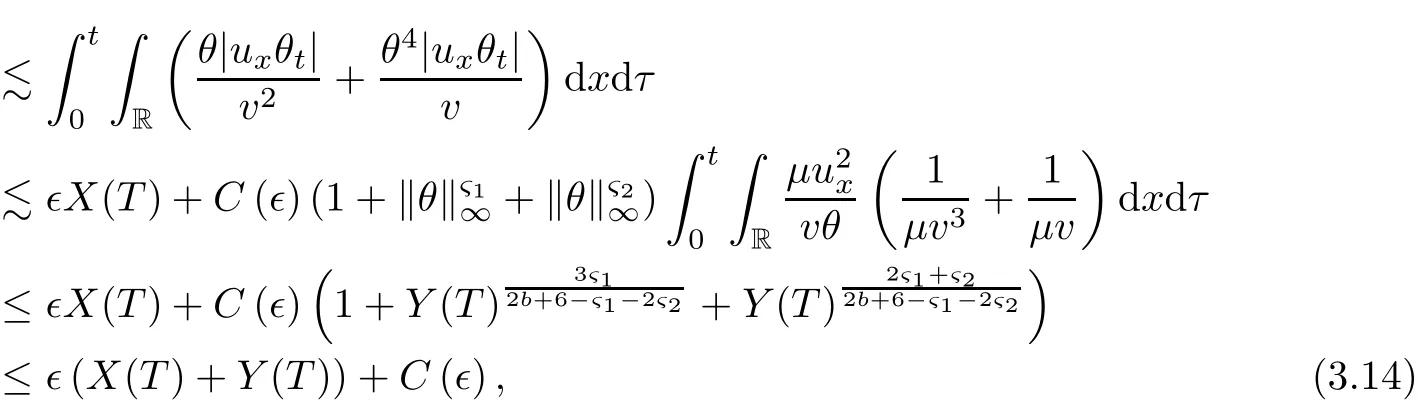



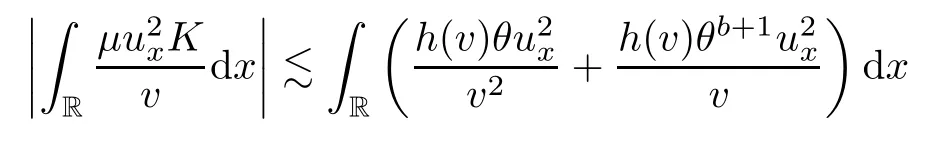

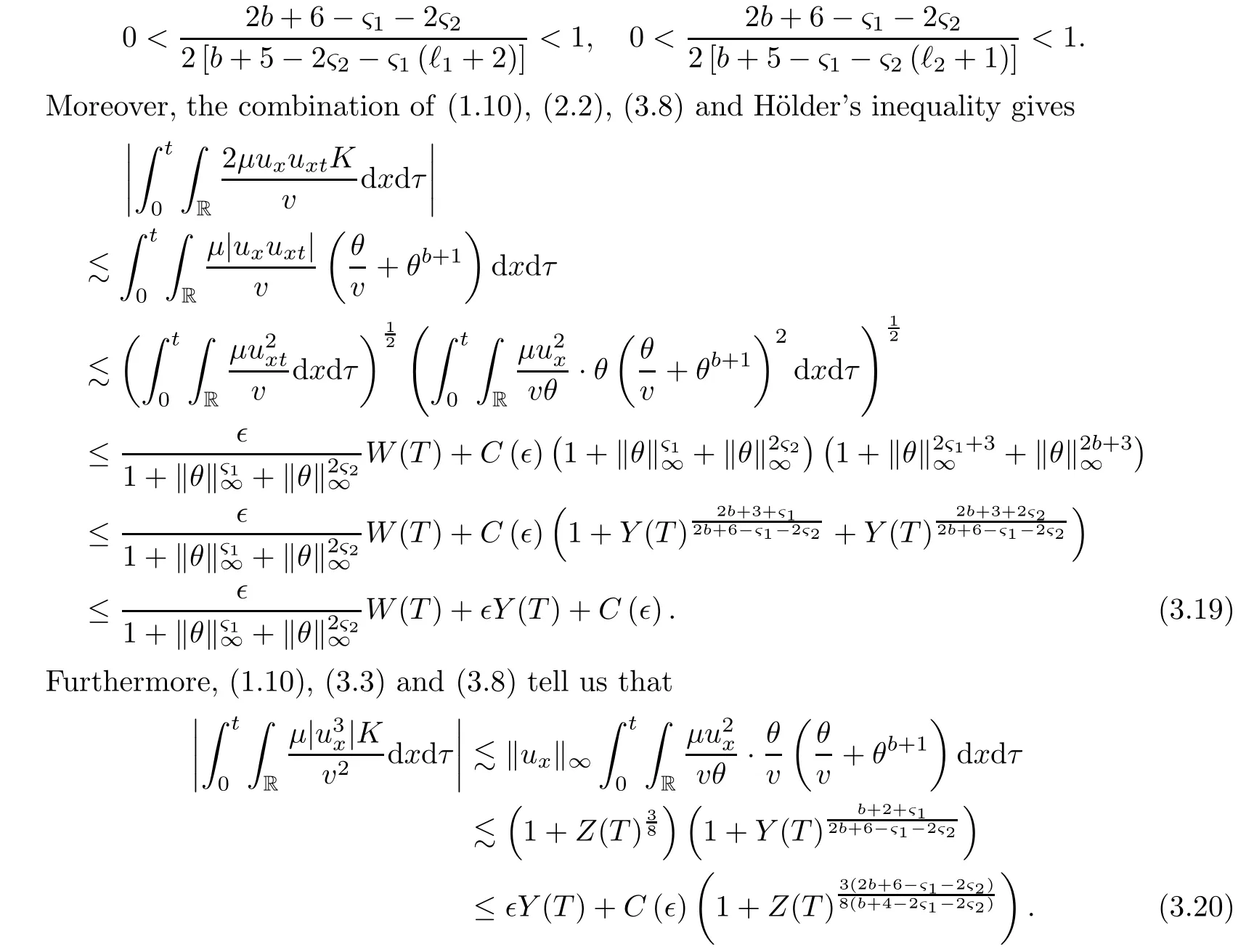



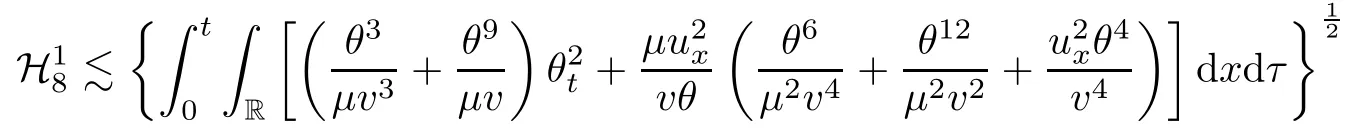
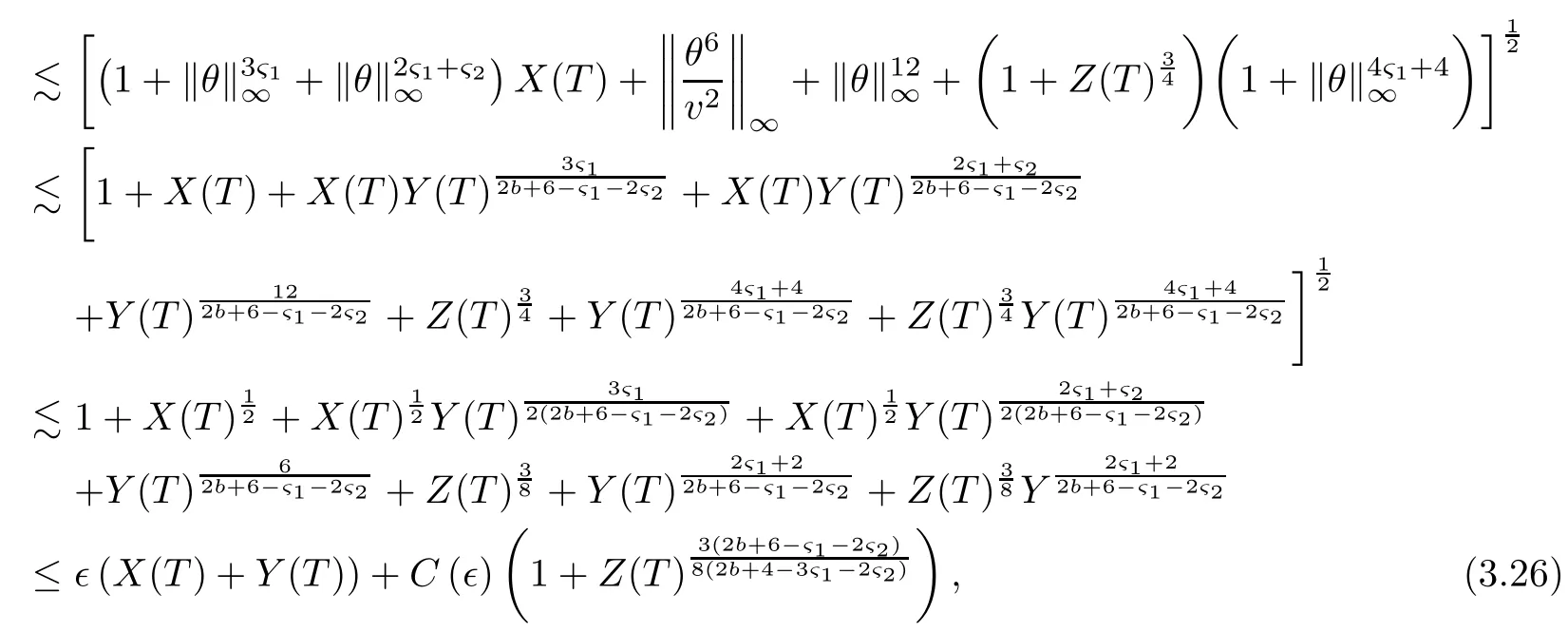




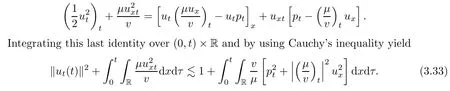
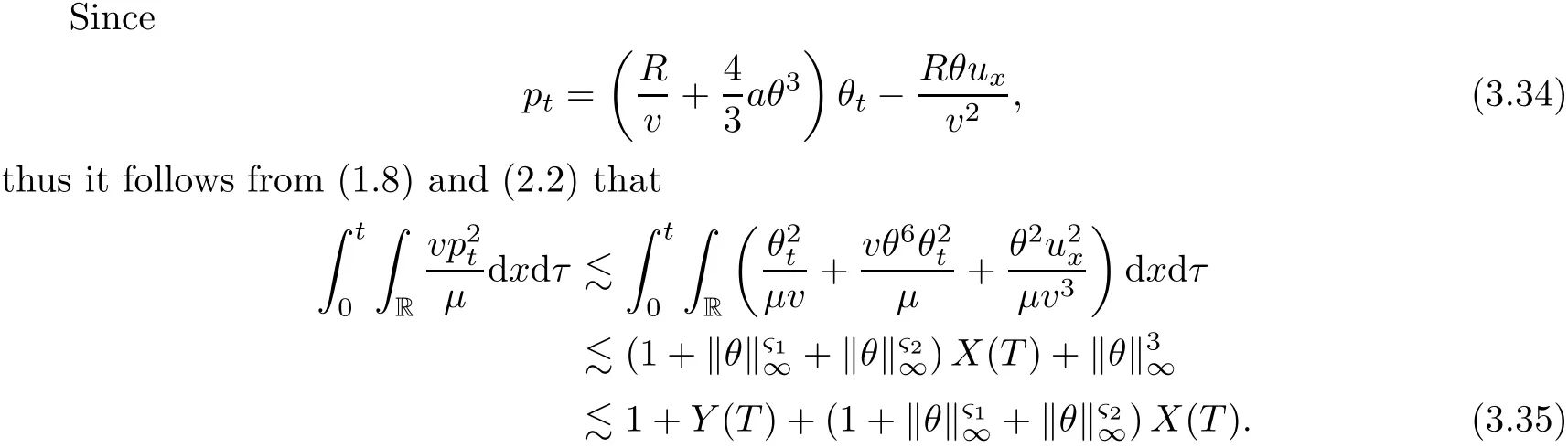





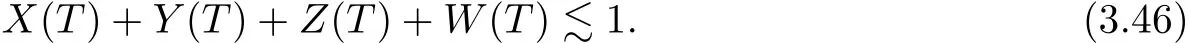




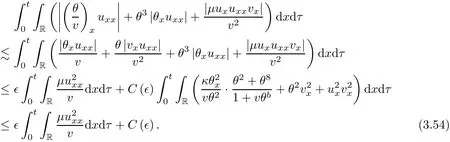



4 Estimates of Second-order Derivatives




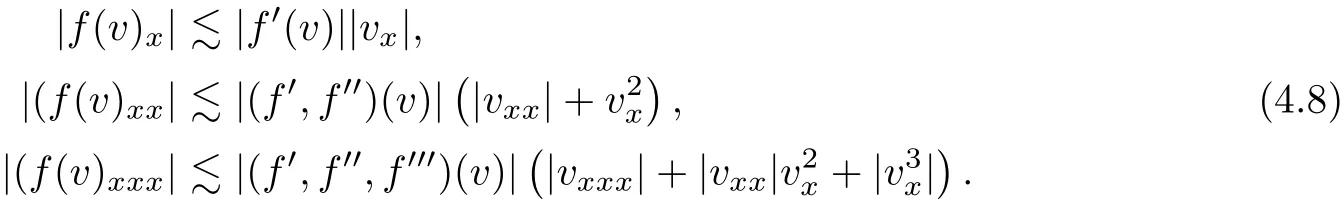


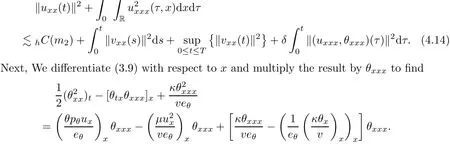


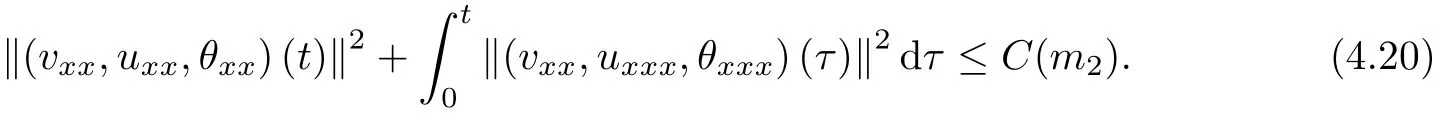

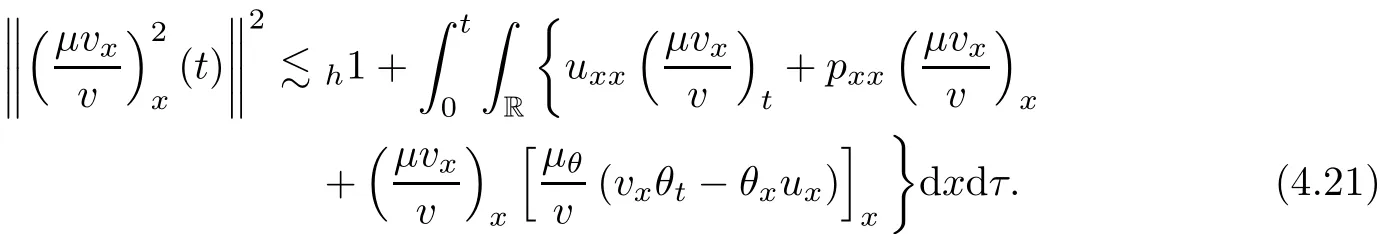
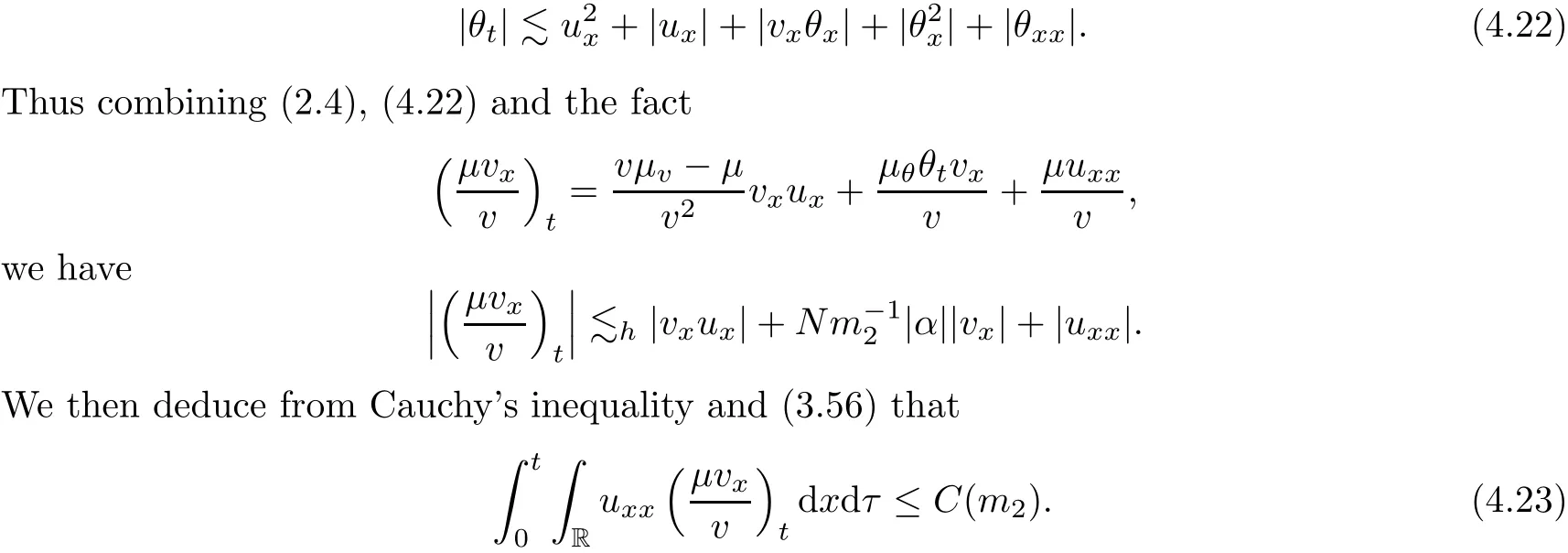



5 Estimates of Third-order Derivatives





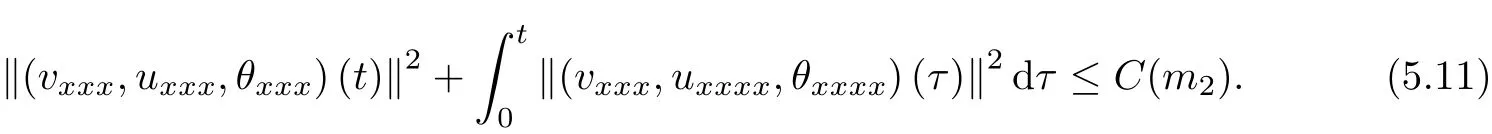
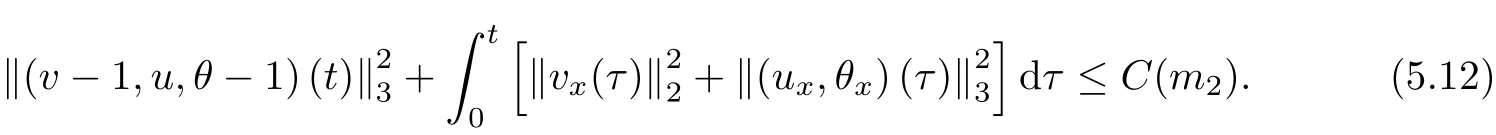
 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
