STABILITY OF STEADY MULTI-WAVE CONFIGURATIONS FOR THE FULL EULER EQUATIONS OF COMPRESSIBLE FLUID FLOW?
Gui-Qiang G.CHEN(陳貴強(qiáng))Matthew RIGBY
Mathematical Institute,University of Oxford,Oxford,OX2 6GG,UK
E-mail:chengq@maths.ox.ac.uk;rigby@maths.ox.ac.uk
Abstract We are concerned with the stability of steady multi-wave con figurations for the full Euler equations of compressible fluid flow.In this paper,we focus on the stability of steady four-wave con figurations that are the solutions of the Riemann problem in the flow direction,consisting of two shocks,one vortex sheet,and one entropy wave,which is one of the core multi-wave con figurations for the two-dimensional Euler equations.It is proved that such steady four-wave con figurations in supersonic flow are stable in structure globally,even under the BV perturbation of the incoming flow in the flow direction.In order to achieve this,we first formulate the problem as the Cauchy problem(initial value problem)in the flow direction,and then develop a modi fied Glimm di ff erence scheme and identify a Glimm-type functional to obtain the required BV estimates by tracing the interactions not only between the strong shocks and weak waves,but also between the strong vortex sheet/entropy wave and weak waves.The key feature of the Euler equations is that the re flection coefficient is always less than 1,when a weak wave of di ff erent family interacts with the strong vortex sheet/entropy wave or the shock wave,which is crucial to guarantee that the Glimm functional is decreasing.Then these estimates are employed to establish the convergence of the approximate solutions to a global entropy solution,close to the background solution of steady four-wave con figuration.
Key words stability;multi-wave con figuration;vortex sheet;entropy wave;shock wave;BV perturbation;full Euler equations;steady;wave interactions;Glimm scheme
1 Introduction
We are concerned with the stability of steady multi-wave con figurationsfor the two-dimensional steady full Euler equations of compressible fluid flow governed by

where(u,v)is the velocity,ρ the density,p the scalar pressure,andthe total energy,with internal energy e that is a given function of(p,ρ)de fined through thermodynamic relations.The other two thermodynamic variables are the temperature T and the entropy S.If(ρ,S)are chosen as two independent variables,then the constitutive relations become

is de fined as the sonic speed.
In this paper,we focus on the stability of steady four-wave con figurations in the two spacedimensional case,consisting of two shocks,one vortex sheet,and one entropy wave,which are the solutions of the Riemann problem in the flow direction;see Figure 1.In this con figuration,the vortex sheet and the entropy wave coincide in the Euler coordinates.This is one of the fundamental core multi-wave con figurations,as a solution of the standard steady Riemann problem for the two-dimensional Euler equations:
(i)For supersonic flow,there are at most eight waves(shocks,vortex sheets,entropy waves,rarefaction waves)that emanate from one single point in the Euler coordinates,which consist of one solution(at most four of these waves)of the Riemann problem in the flow direction and the other solution(at most four of these waves)of the other Riemann problem in the opposite direction,while the later Riemann problem can also be reduced into the standard Riemann problem in the flow direction by the coordinate transformation(x,y) → (?x,?y)and the velocity transformation(u,v)→ (?u,?v),which are invariant for the Euler equations(1.1).
(ii)Vortex sheets and entropy waves are new key fundamental waves in the multidimensional case,which are normally very sensitive in terms of perturbations as observed in numerical simulations and physical experiments(cf.[1,2,5,7,10]).
(iii)Such solutions are fundamental con figurations for the local structure of general entropy solutions,which play an essential role in the mathematical theory of hyperbolic conservation laws(cf.[3,4,6,7,15–19,22,23]).
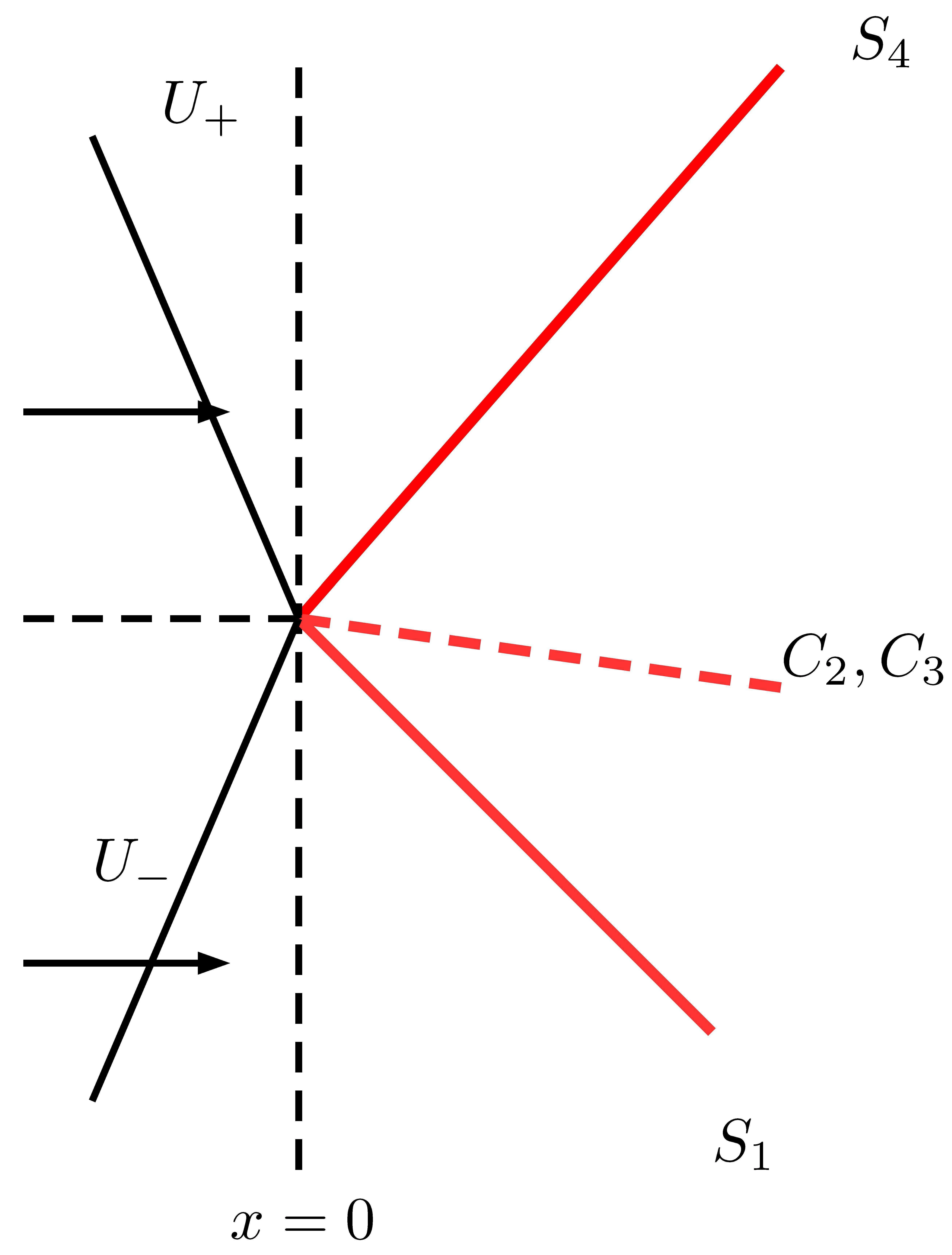
Figure 1 An unperturbed four-wave con figuration,consisting of two shocks S1and S2,one vortex sheet C2,and one entropy wave C3
The stability problem involving supersonic flows with a single shock past a Lipschitz wedge has been solved in Chen–Zhang–Zhu[11](also see Chen–Li[9]).The stability problem involving supersonic flows with vortex sheets and entropy waves over a Lipschitz wall has been solved in Chen–Zhang–Zhu[12].See also Chen–Kuang–Zhang[8]for the stability of two-dimensional steady supersonic exothermically reacting Euler flow past Lipschitz bending walls.
The case of an initial con figuration involving two shocks is treated in[21],by using the method of front tracking,for more general equations,under the finiteness and stability conditions.We think that,with the estimates of Riemann solutions involving more than two strong waves,the estimates on the re flection coefficients of wave interactions should play a similar role so that the method of front tracking may be used.
In this paper,it is proved that steady four-wave con figurations in supersonic flow are stable in structure globally,even under the BV perturbation of the incoming flow in the flow direction.In order to achieve this,we first formulate the problem as the Cauchy problem(initial value problem)in the flow direction,then develop a modi fied Glimm di ff erence scheme similar to those in[11,12]from the original Glimm scheme in[19]for one-dimensional hyperbolic conservation laws,and further identify a Glimm-type functional to obtain the required BV estimates by tracing the interactions not only between the strong shocks and weak waves,but also between the strong vortex sheet/entropy wave and weak waves carefully.The key feature of the Euler equations is that the re flection coefficient is always less than 1,when a weak wave of di ff erent family interacts with the vortex sheet/entropy wave or the shock wave,which is crucial to guarantee that the Glimm functional is decreasing.Then these estimates are employed to establish the convergence of the approximate solutions to a global entropy solution,close to the background solution of steady four-wave con figuration.
This paper is organized as follows:In Section 2,we first formulate the stability of multiwave con figurations as the Cauchy problem(initial value problem)in the flow direction for the Euler equations(1.1)and then state the main theorem of this paper.In Section 3,some fundamental properties of system(1.1)and the analysis of the Riemann solutions are presented,which are used in the subsequent sections.In Section 4,we make estimates on the wave interactions,especially between strong and weak waves,and identify the key feature of the Euler equations that the re flection coefficient is always less than 1,when a weak wave of di ff erent family interacts with the vortex sheet/entropy wave or the shock wave.In Section 5,we develop a modi fied Glimm di ff erence scheme,based on the ones in[11,12],to construct a family of approximate solutions,and establish necessary estimates that will be used later to obtain its convergence to an entropy solution of the Cauchy problem(1.1)and(2.1).In Section 6,we show the convergence of the approximate solutions to an entropy solution,close to the background solution of steady four-wave con figuration.
2 Formulation of the Problem and Main Theorem
In this section,we formulate the stability problem for the steady four-wave con figurations as the Cauchy problem(initial value problem)in the flow direction for the Euler equations(1.1)and then state the main theorem of this paper.
2.1 Stability Problem
We focus on the stability problem of the four-wave con figurations consisting of two strong shocks,one strong vortex sheet,and one entropy wave for the supersonic Euler flows governed by system(1.1)for U=(u,v,p,ρ).More precisely,we consider a background solutionthat consists of four constant states:

where uj>cjfor all j∈{a,m1,m2,b}with the sonic speed of state Uj:
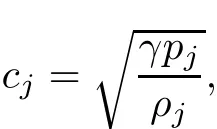
and state Um1connects to Ubby a strong 1-shock of speed σ10,Um1connects to Um2by a strong 2-vortex sheet and a strong 3-entropy wave of strengths(σ20,σ30),and Uaconnects to Um2by a strong 4-shock of speed σ40;see Figure 2.
We are interested in the stability of the background solutionof steady four-wave con figuration,under small BV perturbations of the incoming flow as the initial data,to see whether it leads to entropy solutions containing similar strong four-wave con figurations,close to the background solution ofThat is,the stability problem can be formulated as the following Cauchy problem(initial value problem)for the Euler equations(1.1)with the Cauchy data:

where U0∈ BV(R)is a small perturbation function close to U(·,0)in BV.
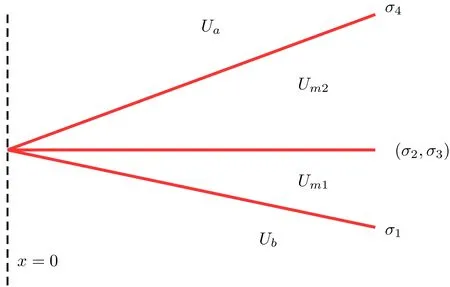
Figure 2 The background solutionconsisting of four waves and four constant states
The main theorem of this paper is the following:
Theorem 2.1(existence and stability) There exist ?>0 and C>0 such that,if U0∈BV(R)satis fies
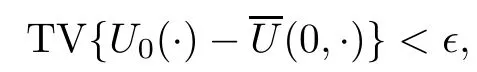
then there are four functions:
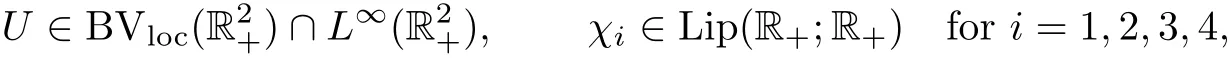
such that
(i)U is a global entropy solution of system(1.1)in,satisfying the initial condition(2.1);
(ii)Curves{y=χi(x)},i=1,2,3,4,are a strong 1-shock,a combined strong 2-vortex sheet and 3-entropy wave(χ2,3:= χ2= χ3),and a strong 4-shock,respectively,all emanating from the origin,with
In Sections 2–6,we prove this main theorem and related properties of the global solution in BV.
3 Riemann Problems and Solutions
This section includes some fundamental properties of system(1.1)and some analysis of the Riemann solutions,which will be used in the subsequent sections;see also[11,12].
3.1 Euler Equations
With U=(u,v,p,ρ),the Euler system can be written in the following conservation form:

where
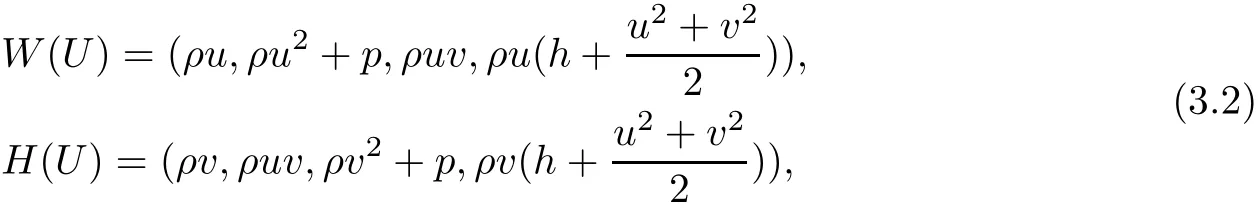
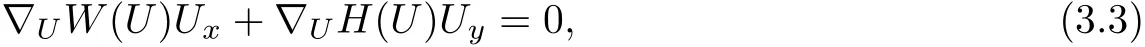
so that the eigenvalues of(3.2)are the roots of the fourth order polynomial:

which are solutions of the equation:

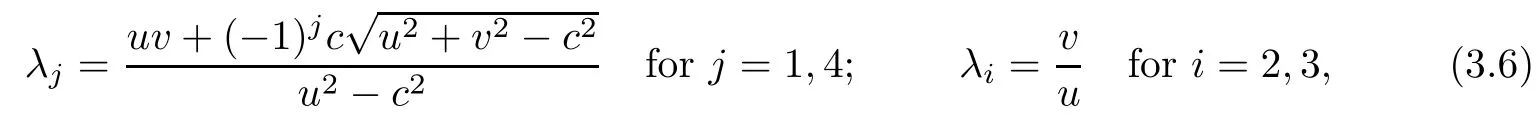
with four corresponding linearly independent eigenvectors:
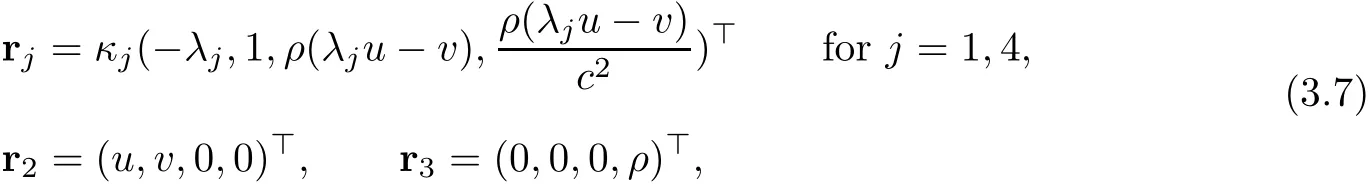
where κjare chosen to ensure that rj·?λj=1 for j=1,4,since the first and fourth characteristic fields are always genuinely nonlinear,and the second and third are linearly degenerate.
In particular,at a state U=(u,0,p,ρ),
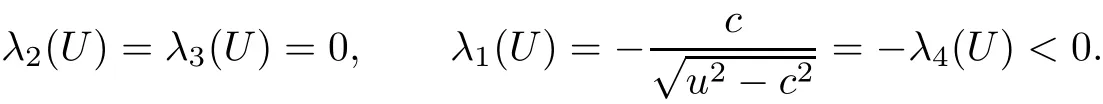
De finition 3.1is called an entropy solution of(1.1)and(2.1)if
(i)U satis fies the Euler equations(1.1)in the distributional sense and(2.1)in the trace sense;
(ii)U satis fies the following entropy inequality:

in the distributional sense in,including the boundary.
3.2 Wave Curves in the Phase Space
In this subsection,based on[11,pp.297–298]and[12,pp.1666–1667],we look at the basic properties of nonlinear waves.
We focus on the region,{u>c},in the state space,especially in the neighborhoods of Ujin the background solution.
We first consider self-similar solutions of(1.1):

which connect to a state U0=(u0,v0,p0,v0).We find that

which implies
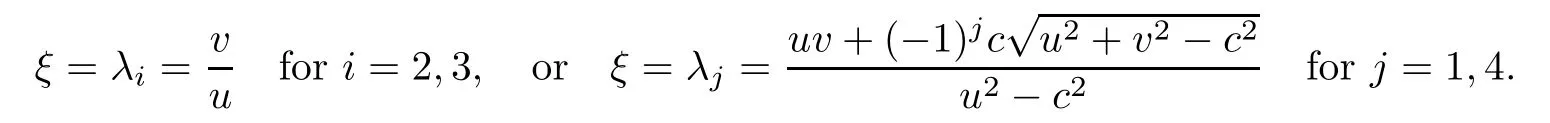
First,for the cases i=2,3,we obtain

This yields the following curves Ci(U0)in the phase space through V0:

which describe compressible vortex sheets(i=2)and entropy waves(i=3).More precisely,we have a vortex sheet governed by
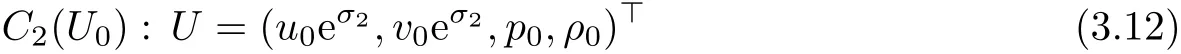
with strength σ2and slope,which is determined by
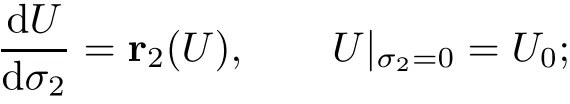
and an entropy wave governed by

with strength σ3and slope,which is determined by

For j=1,4,we obtain the j-th rarefaction wave curve Rj(U0),j=1,4,in the phase space through U0:
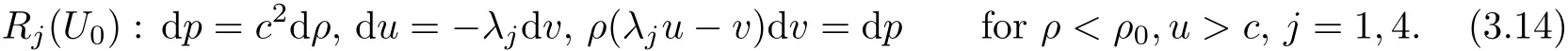
For shock wave solutions,the Rankine-Hugoniot conditions for(1.1)are
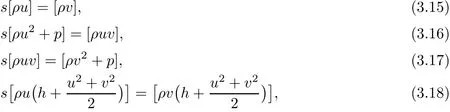
where the jump symbol[·]stands for the value of the front state minus that of the back state.We find that
His primary passion was clear thinking and comprehension. When I was in doubt about a concept that I was teaching him, he said, You must ask the teacher again. Must be clear.


where u0>for small shocks.
For si,i=2,3,in(3.15)–(3.18),we obtain the same Ci(U0),i=2,3,de fined in(3.12)–(3.13),since the corresponding fields are linearly degenerate.
On the other hand,for sj,j=1,4,in(3.15)–(3.18),we obtain the j-th shock wave curve Sj(U0),j=1,4,through U0:

where ρ0< ρ is equivalent to the entropy condition(3.8)on the shock wave.We also know that Sj(U0)agrees with Rj(U0)up to second order and that
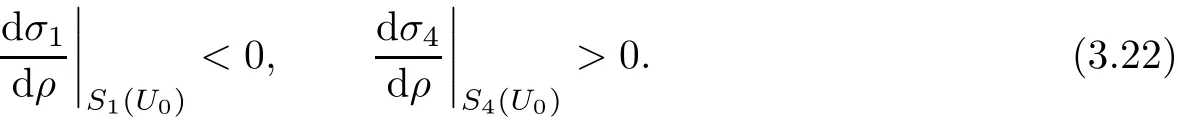
The entropy inequality(3.8)is equivalent to the following:
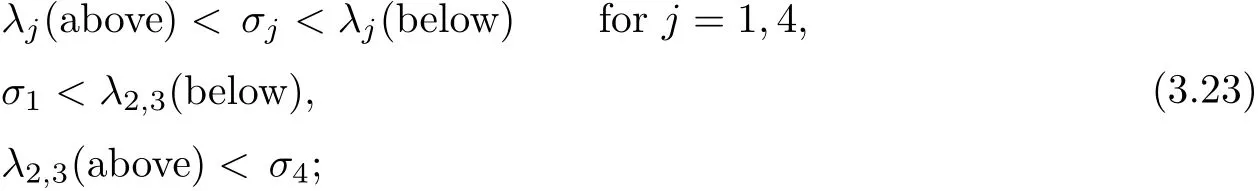
see[11,pp.269–270,pp.297–298]for the details.
3.3 Riemann Problems
We consider the Riemann problem for(1.1):
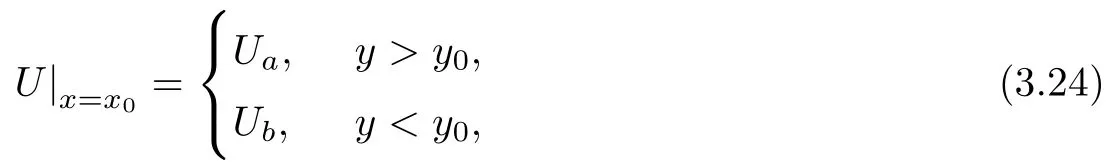
3.3.1 Riemann Problem only Involving Weak Waves
Following Lax[20],we can parameterize any physically admissible wave curve in a neighborhood of a constant state U0.
Lemma 3.2Given U0∈ R4,there exists a neighborhood O?(U0)such that,for all U1,U2∈O?(U0),the Riemann problem(3.24)admits a unique admissible solution consisting of four elementary waves.In addition,state U2can be represented by
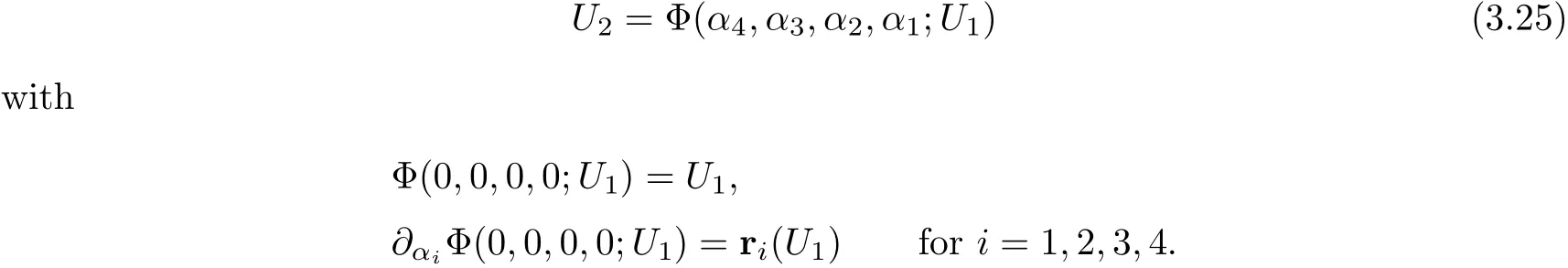
We also note that the renormalization factors κjin(3.7)have been used to ensure that=1 in a neighborhood of any unperturbed statewith u0>0,such as
Lemma 3.3At any statewith u0>0,

which also holds in a neighborhood of U0.
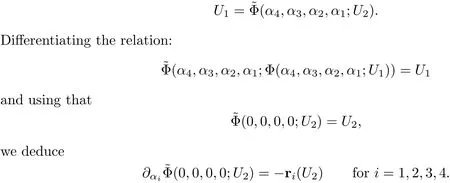
This will be used later in Section 4.We exploit the symmetries between the shock polar and the reverse shock polar,and the symmetry between the 1-shock polar and the reverse 4-shock polar to allow for more concise arguments.
3.3.2 Riemann Problem Involving a Strong 1-shock
The results here are based on those in§6.1.4 of[11],with small changes for our requirements.
For a fixed U1,when,we useto denote the 1-shock that connectswith speed σ1.
Lemma 3.4For allwith
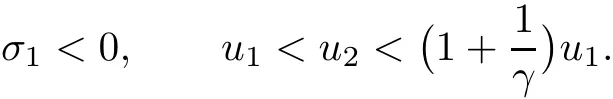
ProofWe follow the same steps as[11,pp.273].First,by(3.20),
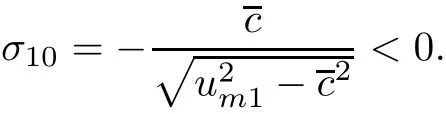
Now,from the Rankine-Hugoniot conditions(3.15)–(3.18),
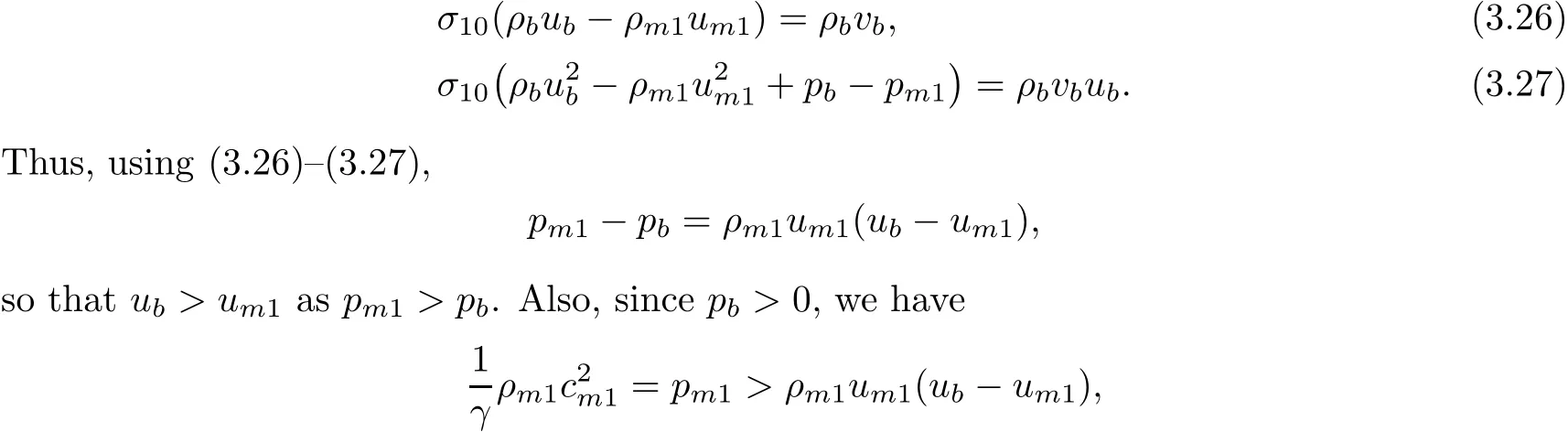
so that,as um1>cm1,
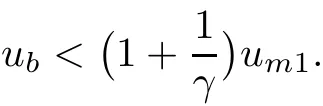
The result now follows by continuity.
Lemma 3.5Let

ProofWe omit the full calculations,which can be found at[11,pp.299–300].We use Lemma 3.4,along with the first and fourth Rankine-Hugoniot conditions(3.15)and(3.18),to deduce that P>0.We then use Lemma 3.4 and the entropy condition(3.23)to deduce
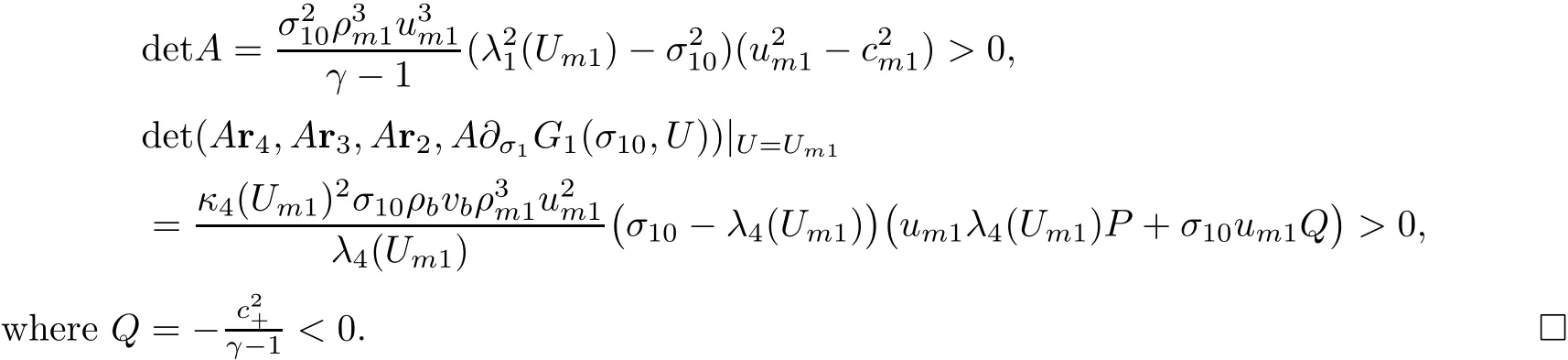
Lemma 3.6There exists a neighborhoodsuch that,for each U0∈O?(Ub),the shock polar S1(Ub)can be parameterized locally for the state which connects to U0by a shock of speed σ10from above as

ProofIt suffices to solve
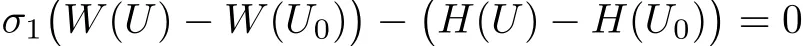
for U in terms of σ1and U0,with the knowledge thatis a solution.We see that
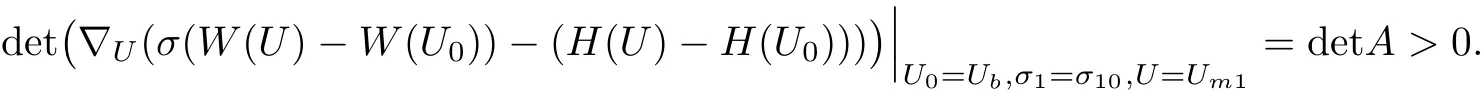
Then the result follows by the implicit function theorem.
3.3.3 Riemann Problem Involving a Strong 4-shock
We now extend our results about 1-shocks to 4-shocks by symmetry.For a fixed U1,whento denote the 4-shock that connects U1to U2with speed σ4.The only di ff erence is the formula for σ4.
Lemma 3.7For allwith
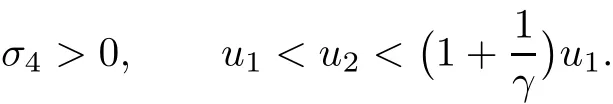
ProofNote that,by(3.23),

Since we have the same Rankine-Hugoniot conditions as in Lemma 3.4,with um2and uataking the roles of um1and ub,respectively,the proof follows identically.
Lemma 3.8There exists a neighborhood O?(Ua) × O??(σ40)such that,for each U0∈O?(Ua),the reverse shock polar–the set of states that connect to U0by a strong 4-shock from blow–can be parameterized locally for the state which connects to U0by a shock of speed σ40as

3.3.4 Riemann Problem Involving Strong Vortex Sheets and Entropy Waves
We now look at the interaction between weak waves and the strong vortex sheet/entropy wave,based on those in §2.5 of[12].For any U1∈ O?(Um1)and U2∈ O?(Um2),we useto denote the strong vortex sheet and entropy wave that connect U1to U2with strength(σ2,σ3).That is,

By a straightforward calculation,we have
Lemma 3.9For
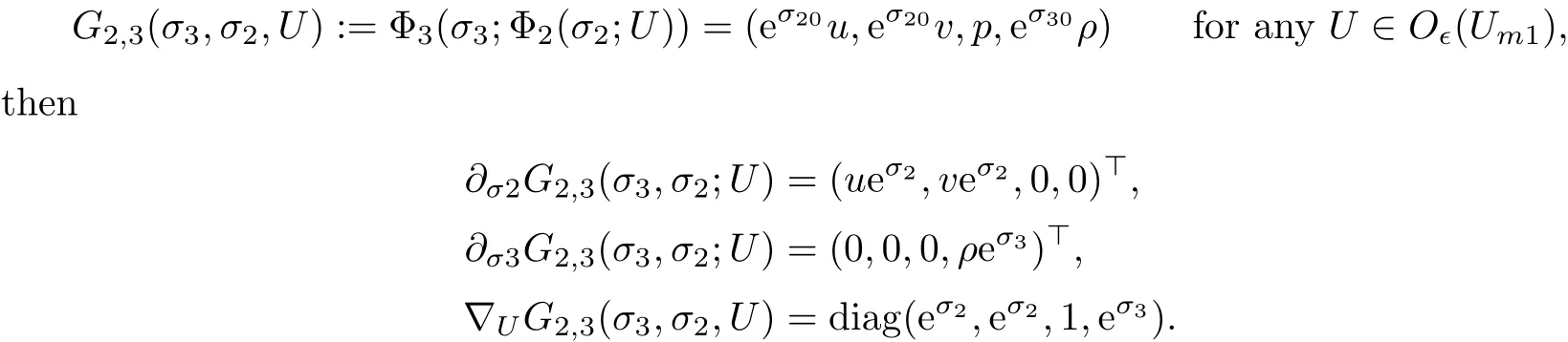
The next property allows us to estimate the strength of re flected weak waves in the interactions between the strong vortex sheet/entropy wave and weak waves:
Lemma 3.10The following holds
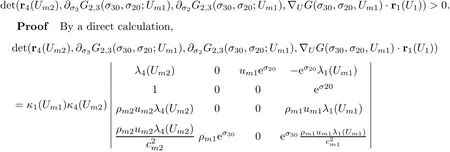
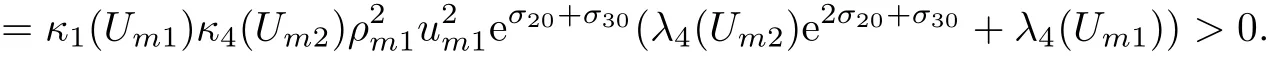
4 Estimates on the Wave Interactions
In this section,we make estimates on the wave interactions,especially between the strong and weak waves.This is based on those in§3 of[11,12],with new estimates for the strong 4-shock.
Below,M>0 is a universal constant which is understood to be large,and O?(Ui)for i∈{a,m1,m2,b}is a universal small neighborhood of Uiwhich is understood to be small.Each of them depends only on the system,which may be di ff erent at each occurrence.

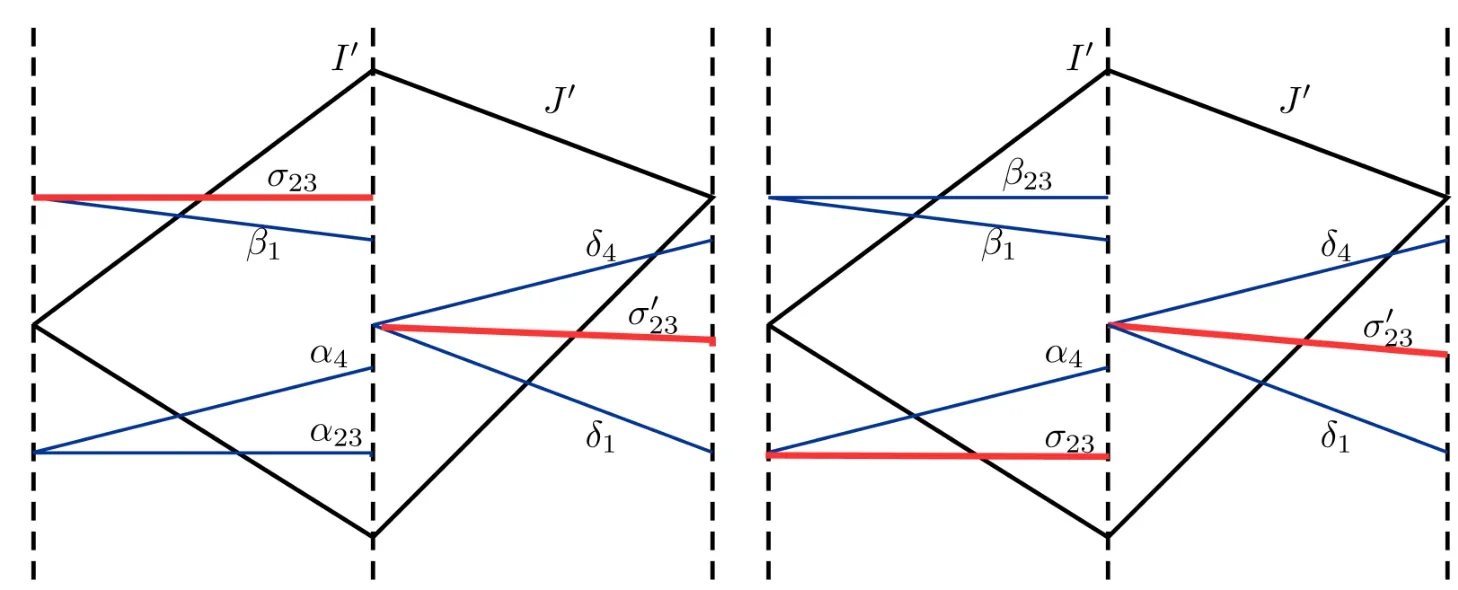
Figure 3 Interaction estimates
4.1 Preliminary Identities
To make later arguments more concise,we now state some elementary identities here to be used later;these are simple consequences of the fundamental theorem of calculus.
Lemma 4.1The following identities hold:
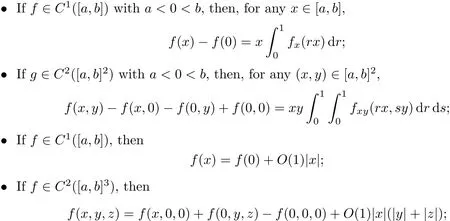
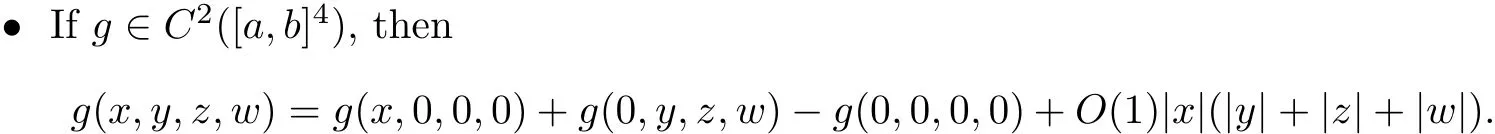
4.2 Estimates on Weak Wave Interactions
We have the following standard proposition;see,for example,[23,Chapter 19]for the proof.Note that,in our analysis of the Glimm functional,we only require the estimates for the cases where the waves are approaching.
Proposition 4.2Suppose that U1,U2,and U3are three states in a small neighborhood of a given state U0with
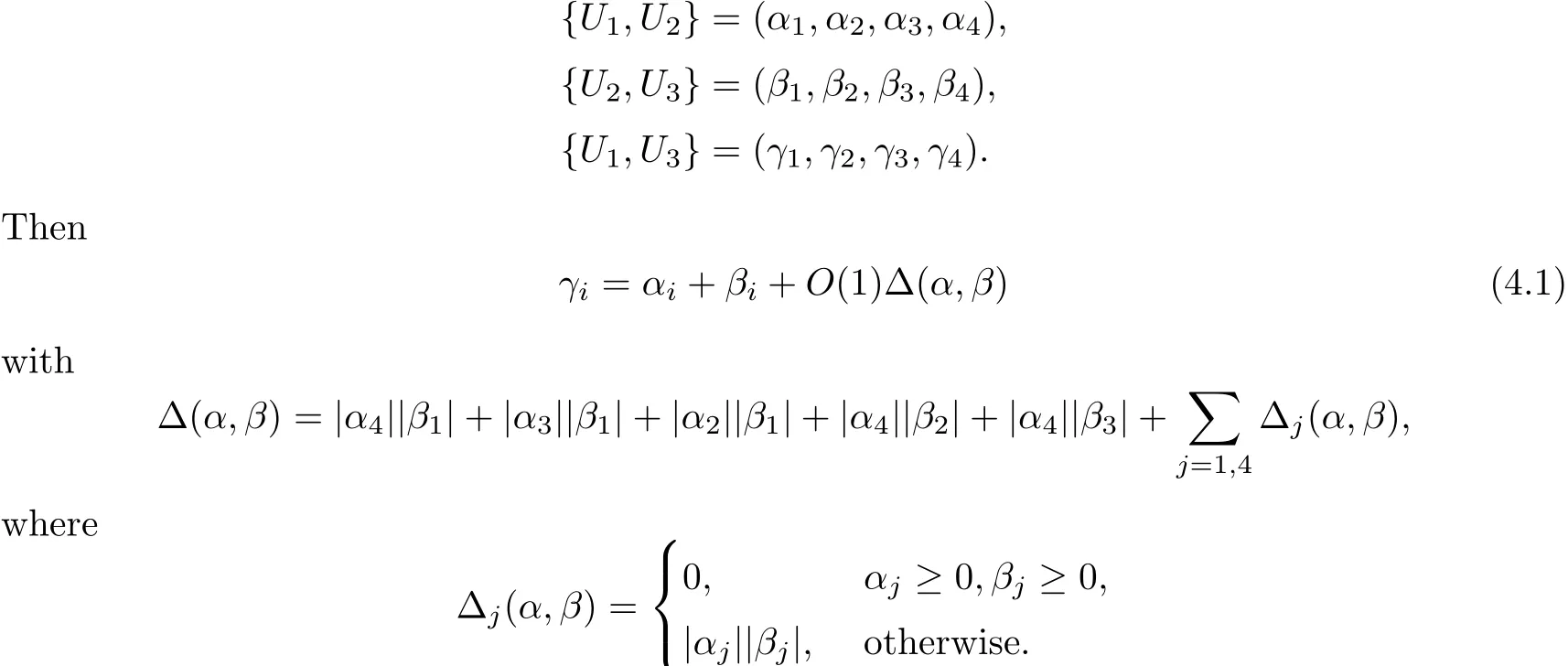
4.3 Estimates on the Interaction between the Strong Vortex Sheet/Entropy Wave and Weak Waves
We now derive an interaction estimate between the strong vortex sheet/entropy wave and weak waves.The properties thatin(4.5)will be critical in the proof that the Glimm functional is decreasing.
Proposition 4.3Let

ProofThis proof is the same as[12,pp.1673],with additional terms.We need to solve foras a function ofin the following equation:

We see that Kvbiand Kbvjare bounded from the formulae above.To deduce that|Kvb1|<1,we di ff erentiate(4.3)with respect to α4to obtain

We can then deduce the following result by symmetry:
Proposition 4.4If

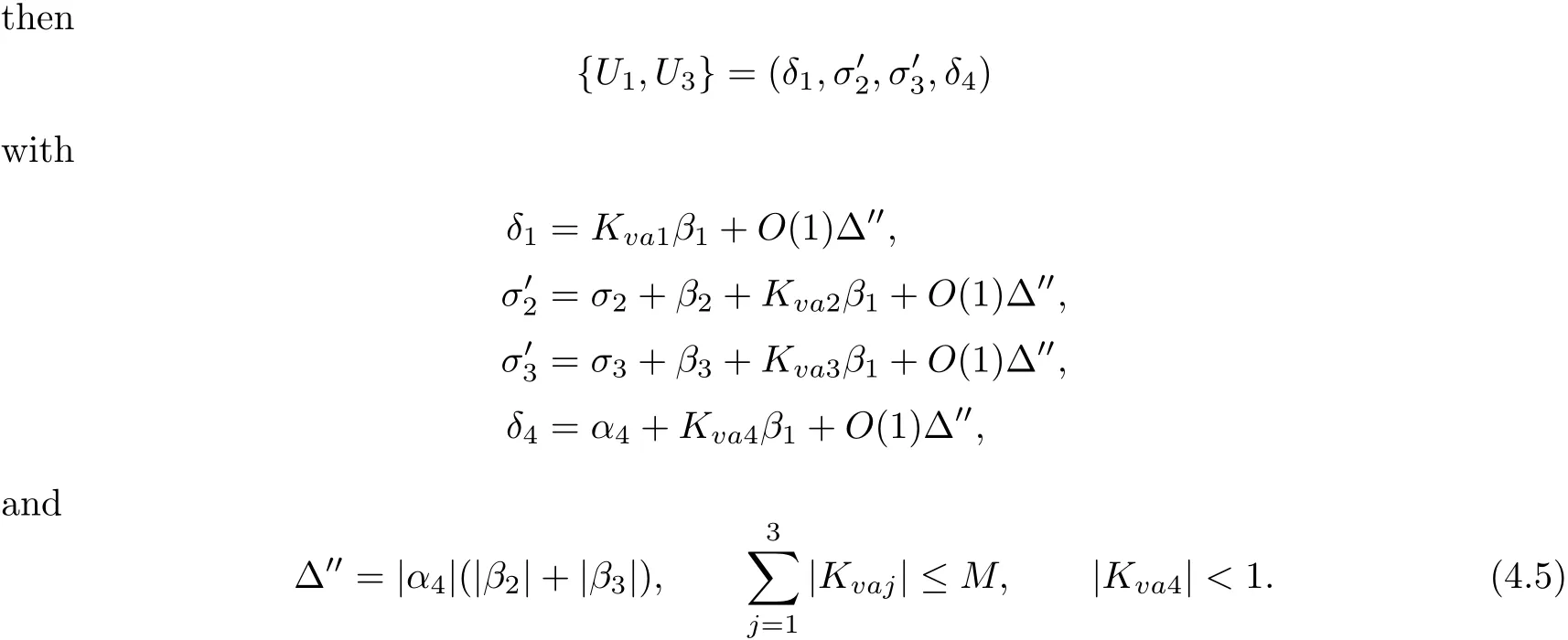
4.4 Estimates on the Interaction between the Strong Shocks and Weak Waves
We now derive an interaction estimate between the strong shocks and weak waves.The properties thatin(4.14)will be critical in the proof that the Glimm functional is decreasing.
4.4.1 Interaction between the Strong 1-shock and Weak Waves
Proposition 4.5If

ProofThis is similar to[11,pp.303],with extra terms.We need to show that there exists a solutionto
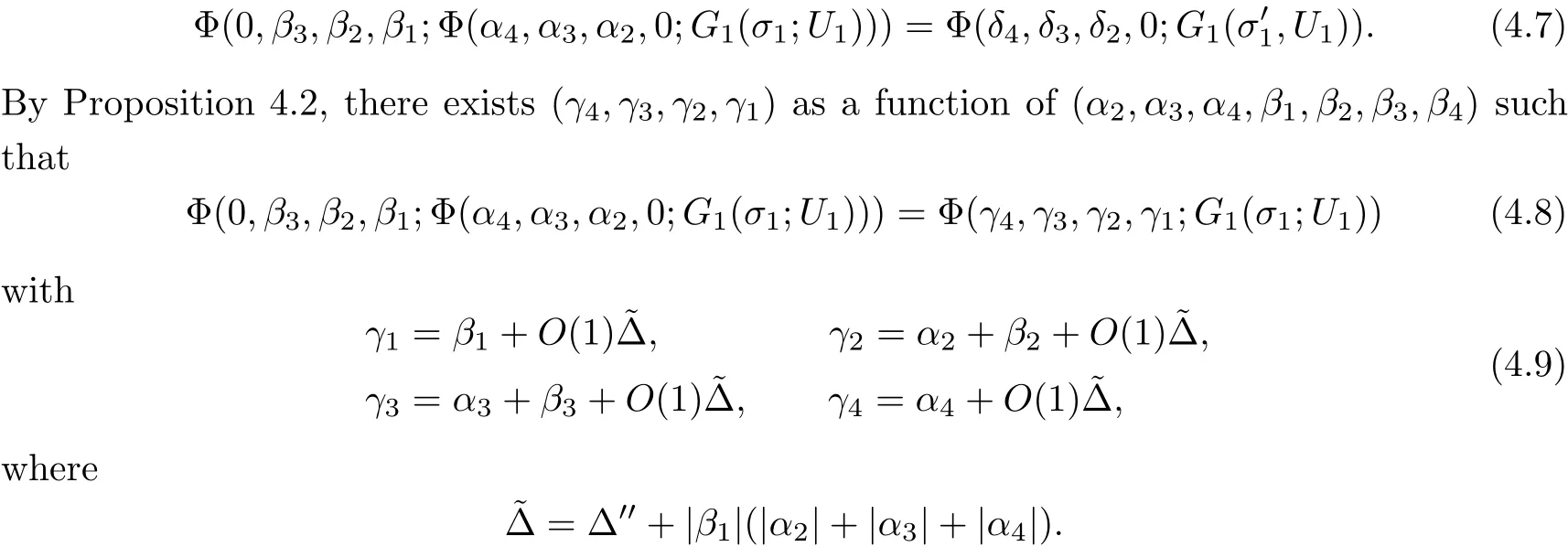
Thus,we may reduce(4.7)to

Now,using the expression of γ in terms of(α,β)and absorbing the residual part of the–term into the,we have the desired result.
We now prove a result for the case where weak waves approach the strong 1-shock from below.
Proposition 4.6Suppose that
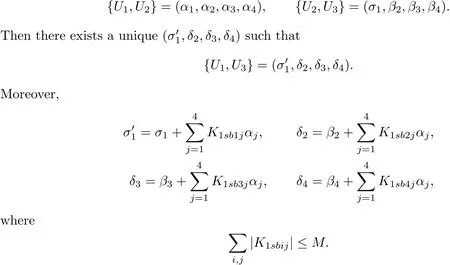
ProofWe need to find a solution to
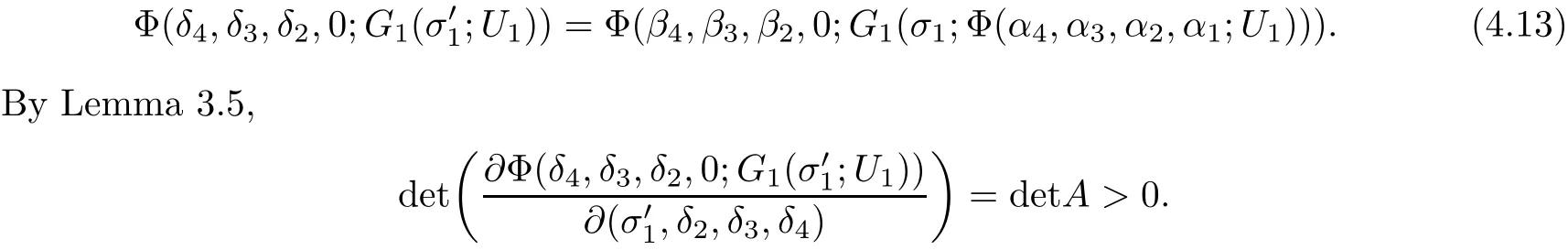
Now the required result follows by using Lemma 4.1,and noting thatα4=0 and thatis a solution.
4.4.2 Interaction between the Strong 4-shock and Weak Waves
Now,by symmetry with the 1-shock case,we deduce the following results:
Proposition 4.7Suppose thatsuch that
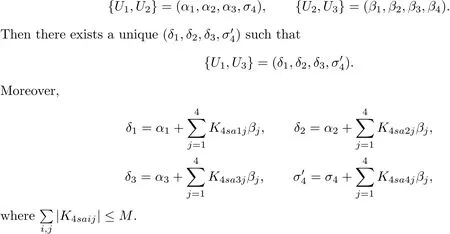
Proposition 4.8If

5 Approximate Solutions and BV Estimates
In this section,we develop a modi fied Glimm di ff erence scheme,based on the ones in[11,12],to construct a family of approximate solutions and establish necessary estimates that will be used later to obtain its convergence to an entropy solution to(1.1)and(2.1).
5.1 A Modi fied Glimm Scheme
For?x>0,we de fine
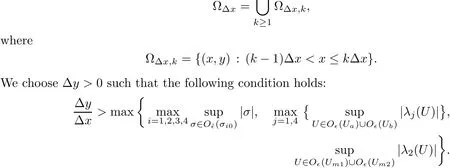
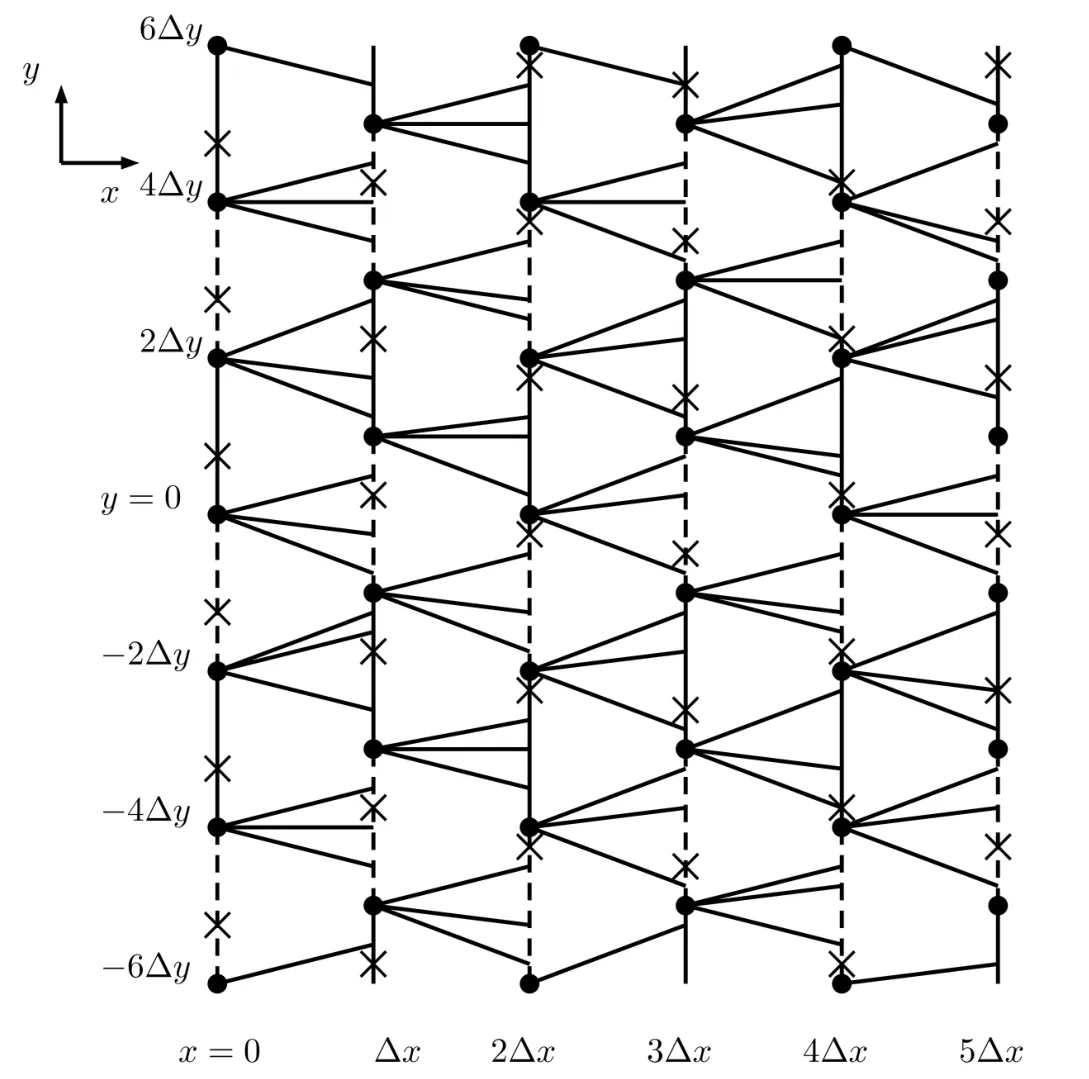
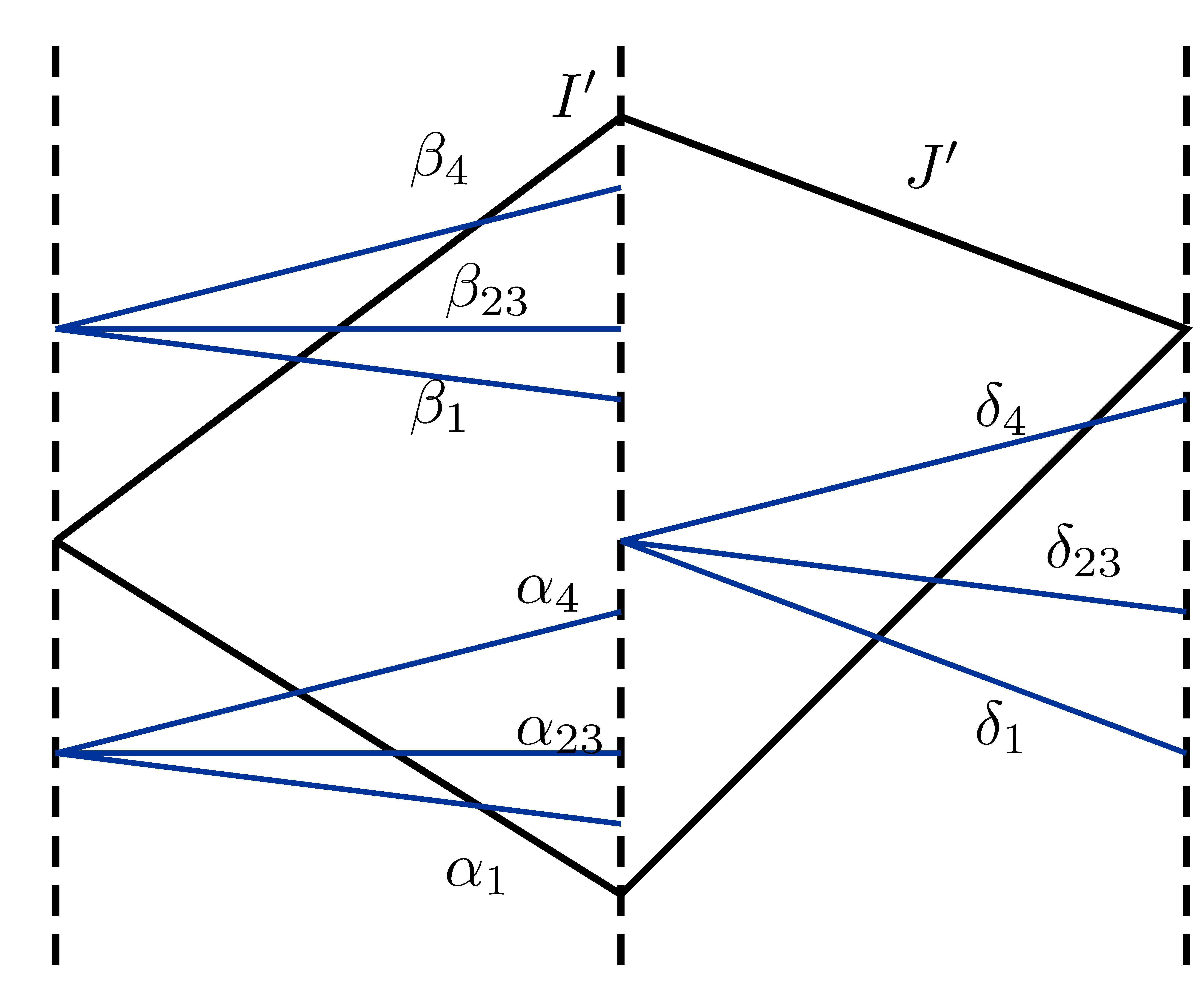
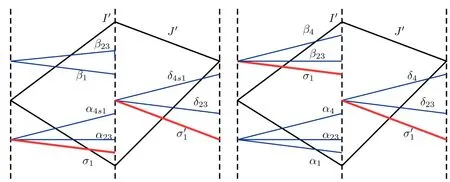
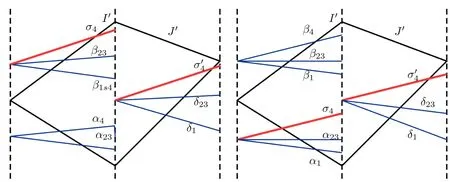
We also need to make sure that the strong shocks do not interact:If we take the neighborhoods small enough,there exist a and b with?1 Now de fine where θkis randomly chosen in(?1,1).We then choose to be the mesh points,and de fine the approximate solutionsfor any θ=(θ0,θ1,···)in the following inductive way: To avoid the issues of interaction of strong fronts,we separate out the initial data for k=0.De fineas follows: Then de fine U0(y)to be the state that connects to U0(?4?y)by a strong 1-shock of strength σ10on(?4?y,0)which lies in O?(Um1),and the state that connects to U0(0)by a combined strong vortex sheet/entropy wave of strengthon(0,4?y)which lies in.Thus,for ? small, Now,as long as we can provide a uniform bound on the solutions and show the Riemann problems involved always have solutions,this algorithm de fines a family of approximate solutions globally. Figure 4 Glimm’s scheme In this section,we prove the approximate solutions are well de fined in ??xby uniformly bounding them.We first introduce the following lemma,which is a combination of Lemma 6.7 in[11,pp.305]and Lemma 4.1 in[12,pp.1677],and follows from that Φ,G1,G2,3,and G4are C1functions. Lemma 5.1The following bounds of the approximate solutions of the Riemann problems hold: We now show that U?x,θcan be de fined globally.Assume that U?x,θhas been de fined in,by the steps in Section 5,and assume the following conditions are satis fied: C1(k ? 1) In each,there are a strong 1-shocka combined strong vortex sheet/entropy waveand a strong 4-shockwith strengthswhich divide ??x,jinto four parts:– the part below–the part between–the part betweenand–the part above To see that C2(k)holds if C2(k?1)holds,by the discussion earlier,forto emanate further down thanwe require θk>b,which implies thatemanate further down thanto emanate further up thanwe require θk We will establish a bound on the total variation of U?x,θon the k-mesh curves to establish C3(k)and C1(k). De finition 5.2A k-mesh curve is an unbounded piecewise linear curve consisting of line segments between the mesh points,lying in the strip: with each line segment of form Figure 5 Separation of the initial data Clearly,for any k>0,each k-mesh curve I divides plane R2into a part I+and a part I?,where I?is the one containing set{x<0}.As in[19],we partially order these mesh curves by saying J>I if every point of J is either on I or contained in I+,and we call J an immediate successor to I if J>I and every mesh point of J,except one,is on I.We now de fine a Glimm-type functional on these mesh curves. De finition 5.3De fine where|α4s1|and|α1s4|are the strengths of the weak 4-shock and 1-shock that emanate from the same point as the strong 1-shock and 4-shock,respectively,and these two weak waves are excluded from,respectively. Remark 5.4measures the total variation of U|J,owing to Lemma 5.1;each term Li(J)measures the total variation in region(i),and each termmeasures the magnitude of jumps of U between the regions separated by the large shocks.We also see that Q(J)≤L(J)for L(J)small enough,so that Q(J)is equivalent to Proposition 5.5Suppose that I and J are two k–mesh curves such that J is an immediate successor of I.Suppose that Let Λ be the diamond that is formed by I and J.We can assume thatsuch thatWe divide our proof into di ff erent cases,based on where diamond Λ is located. Case 1Weak-weak interaction Suppose that Λ lies in the interior of a region(i);see Figure 6.Then,by Proposition 4.2, Figure 6 Case 1:Weak wave interaction Case 2Weak waves interact with the strong vortex sheet/entropy wave from below Suppose that the approximate strong vortex sheet/entropy wave enters Λ from above;see Figure 7. Figure 7 Cases 2&3:Weak waves interact with the strong vortex sheet/entropy wave from below and above We have Case 3Weak waves interact with the strong vortex sheet/entropy wave from above Suppose that the approximate vortex sheet/entropy wave enters Λ from below;see Figure 7.This case follows by symmetry from the above case,owing to the symmetry between Propositions 4.3 and 4.4,and the symmetry between the coefficients. Case 4Weak waves interact with the strong 1-shock from above Suppose that the strong 1-shock enters Λ from below;see Figure 8.By Proposition 4.5,we have Figure 8 Cases 4&5:Weak waves interact with the strong 1-shock from above and below Case 5Weak waves interact with the strong 1-shock from below Suppose that the strong 1-shock enters Λ from above;see Figure 8.By Proposition 4.6,we have Case 6Weak waves interact with the strong 4-shock from below Suppose that the strong 4-shock enters Λ from above;see Figure 9.By symmetry from Case 4,we conclude thatdue to the symmetry between Propositions 4.5 and 4.8. Figure 9 Cases 6&7:Weak waves interact with the strong 4-shock from below and above. Case 7Weak waves interact with the strong 4-shock from above Suppose that the strong 4-shock enters Λ from below;see Figure 9.By symmetry from Case 5,we obtain that,owing to the symmetry between Propositions 4.6 and 4.7. Let Ikbe the k–mesh curve lying inFrom Proposition 5.5,we obtain the following theorem for any k≥1: Theorem 5.6LetK,and C?be the constants speci fied in Proposition 5.5.If the induction hypotheses Moreover,we obtain the following theorem by the construction of our approximate solutions: Theorem 5.7There exists ?>0 such that,if the modi fied Glimm scheme de fines a family of strong approximate frontsand(5.1).In addition, for any x≥0 and h>0. Then,by the estimates in Proposition 5.5,we have Proposition 5.8There exists,independent of?x,θ,and U?x,θ,such that ProofWe follow the proof in[11,pp.290].For any k≥1,and the interaction diamondde fine Therefore,we also conclude the following: Proposition 5.9There existsindependent of?x,θ,and U?x,θ,such that,for j=1,2,3,4, ProofFor j=1,4,this follows immediately from Proposition 5.8.For j=2,3,observe that,if we makesmall enough so thatwe have In this section,we show the convergence of the approximate solutions to an entropy solution close to the four-wave con figuration solution. Lemma 6.1For any h>0 and x≥0,there exists a constantˇN,independent of?x,θ,and h,such that ProofBy Fubini’s theorem and Theorem 5.7, Then,summing over all k and n with k+n≡1(mod2)and re-arranging the terms,we have Following the same steps as in[23,Chapter 19],we have Lemma 6.2There exist a null setand a subsequencewhich tends to 0,such that To complete the proof of the main theorem,we need to estimate the slope of the approximate strong fronts.For k≥1,i=1,2,3,4, Lemma 6.3The following statements hold: ProofThe first part is a direct calculation.The second follows by the same proof as[11,pp.292];just take two sub-sub-sequences to obtain all three strong front slopes to converge. Theorem 6.4(existence and stability) There exist ?>0 and C>0 such that,if the hypotheses of the main theorem hold,then,for eachthere exists a sequenceof mesh sizes with?l→ 0 as l→ ∞,and functionssuch that (i)U?l,θconverges to Uθa.e.in R2+,and Uθis a global entropy solution of system(1.1)and satis fies the initial data(2.1)a.e.; (ii) χj,?l,θconverges to χj,θuniformly in any bounded x-interval; (iii)sj,?l,θconverges to sj,θ∈ BV([0,∞))a.e.andR ProofResult(i)follows by the same steps as[23,Chapter 19],(ii)follows by Theorem 5.7 and the Arzela-Ascoli theorem,while(iii)follows Proposition 5.9 and the basic properties of BV functions. ?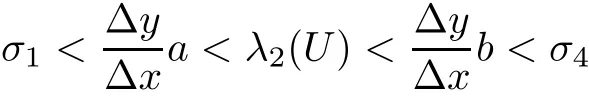

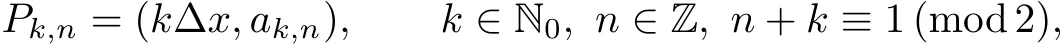

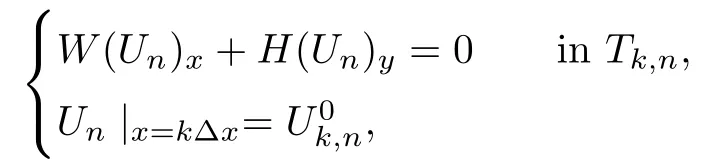
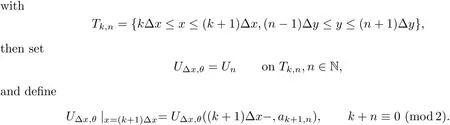
5.2 Glimm-type Functional and Its Bounds
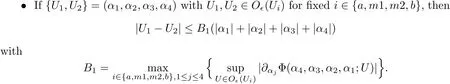
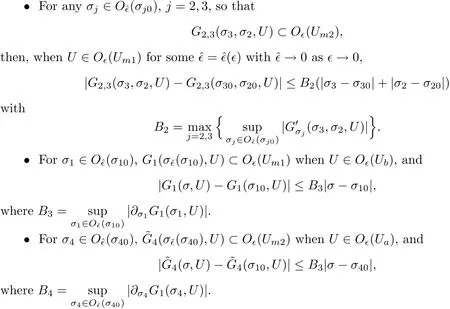

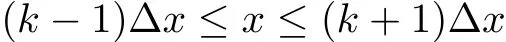



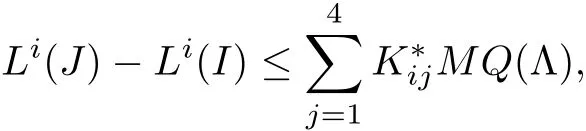
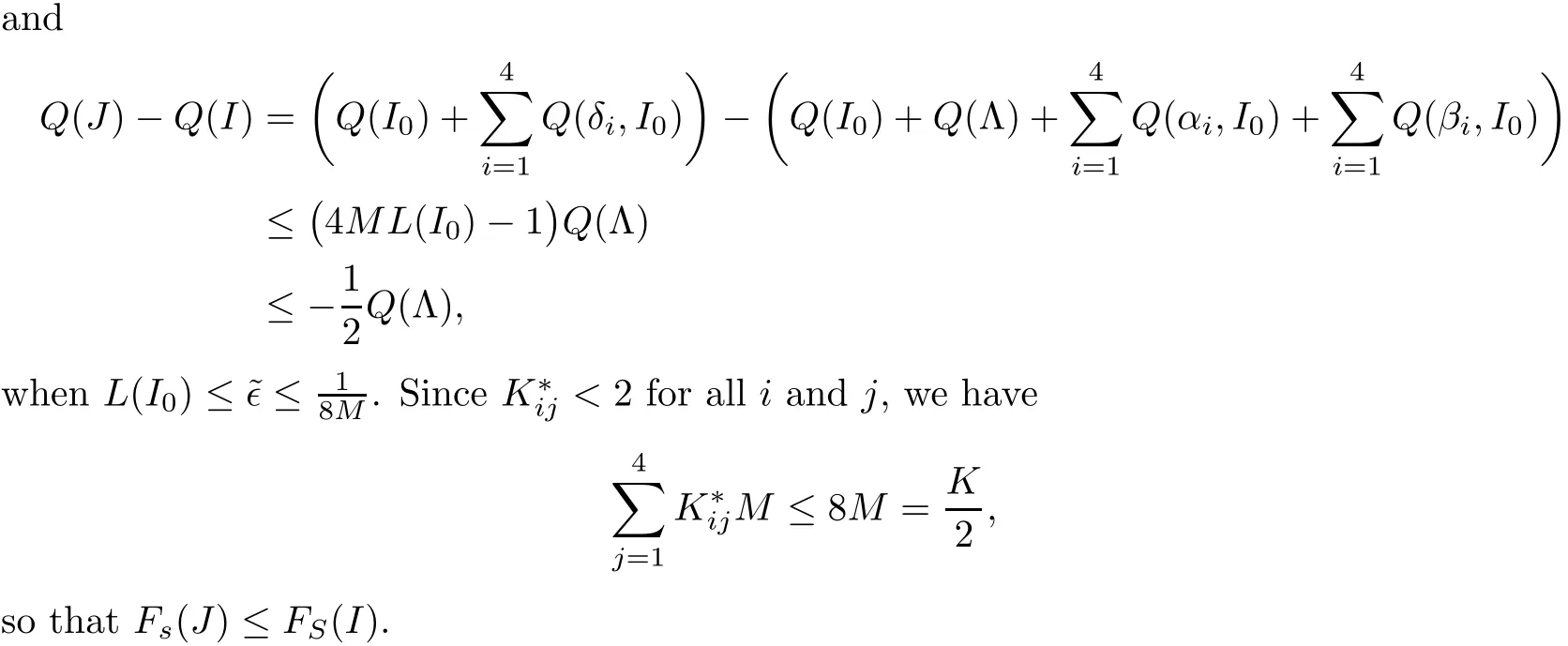
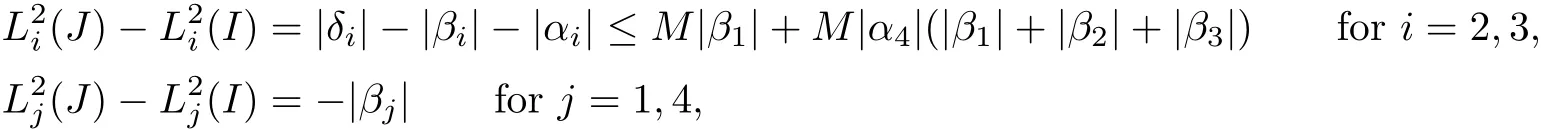
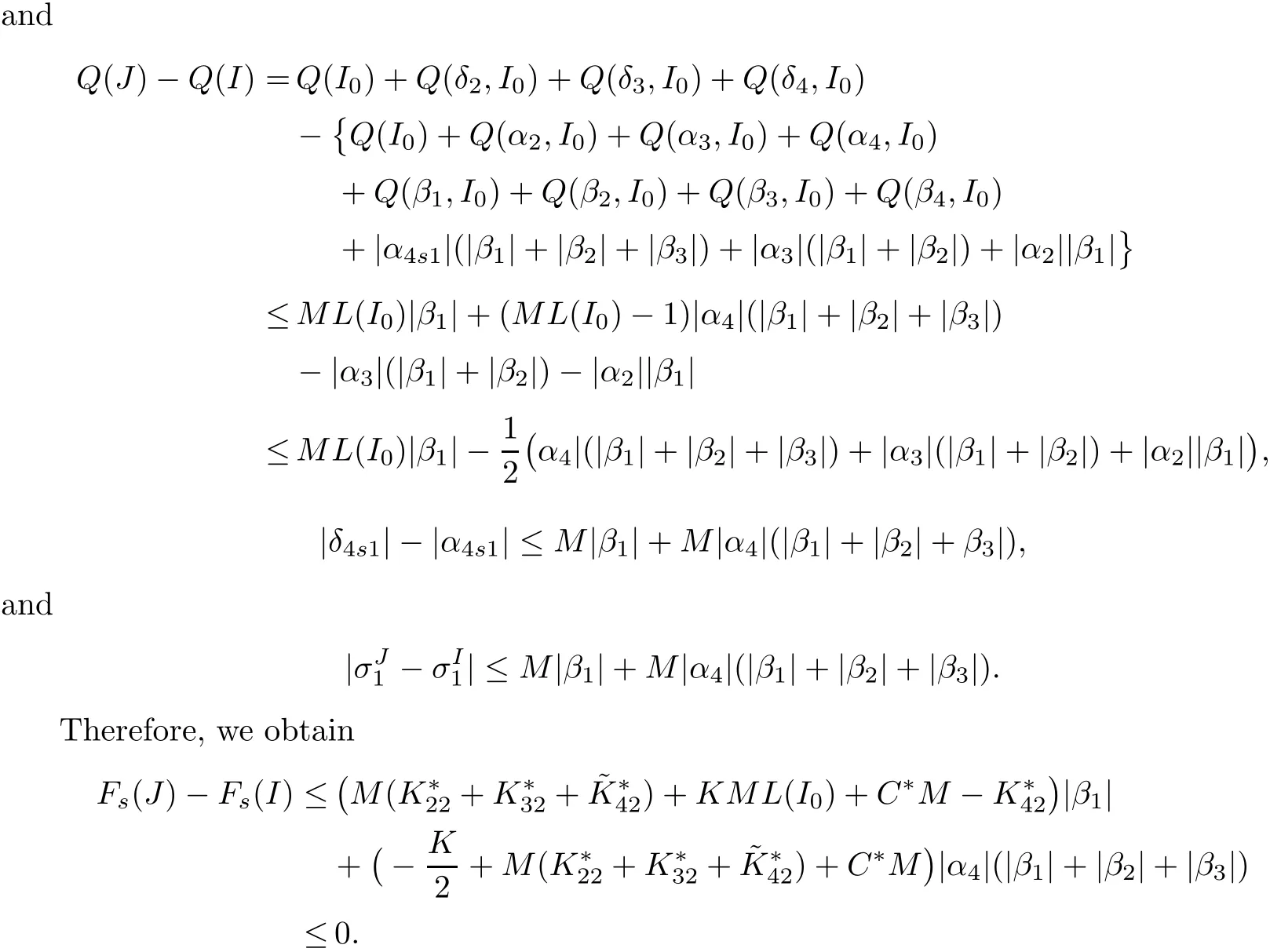
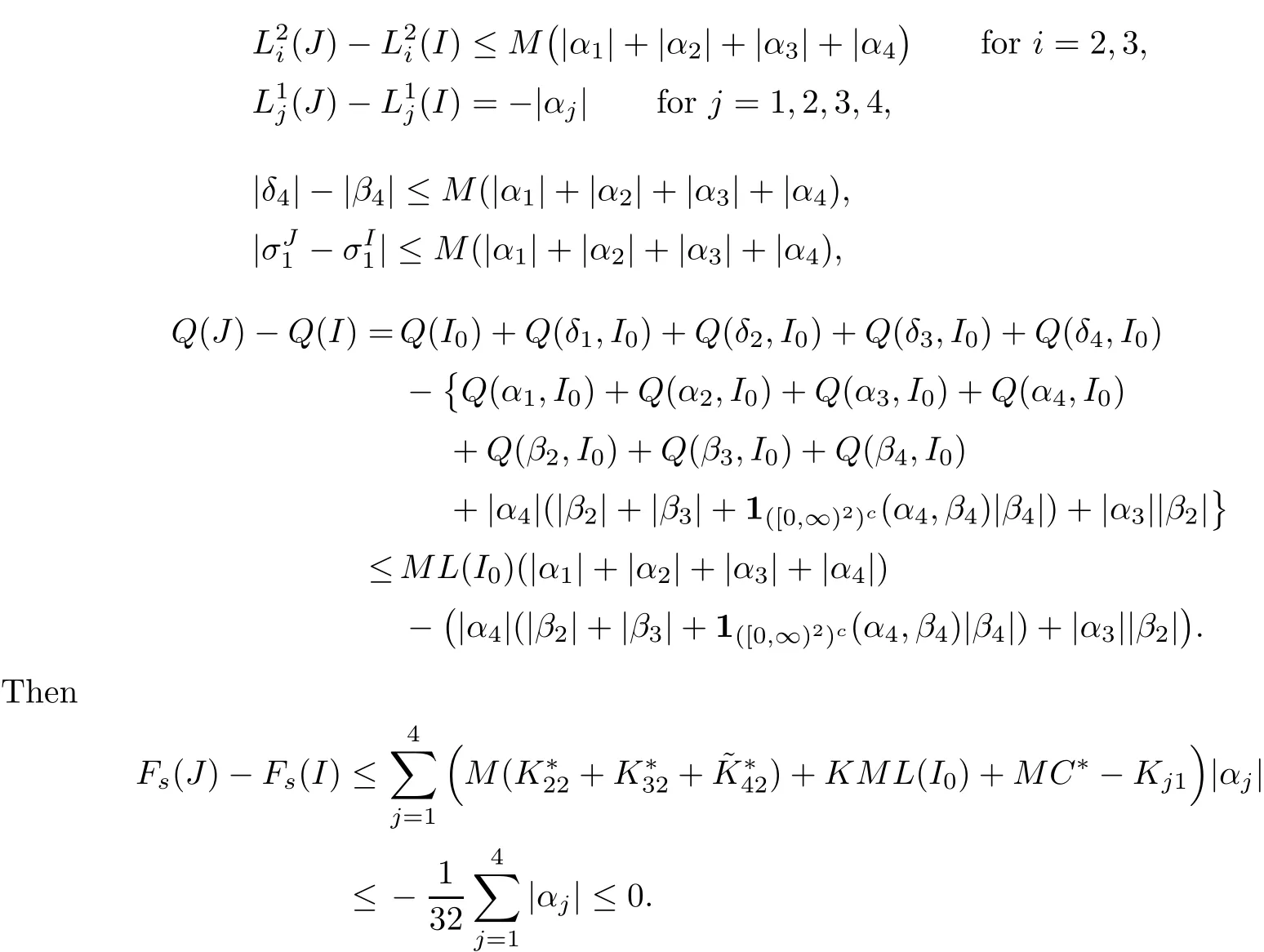
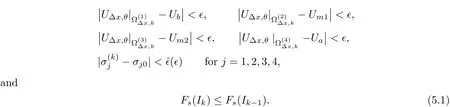
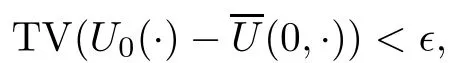
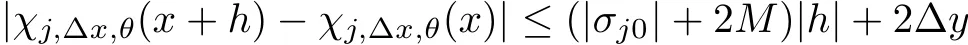
5.3 Estimates on the Approximate Strong Fronts
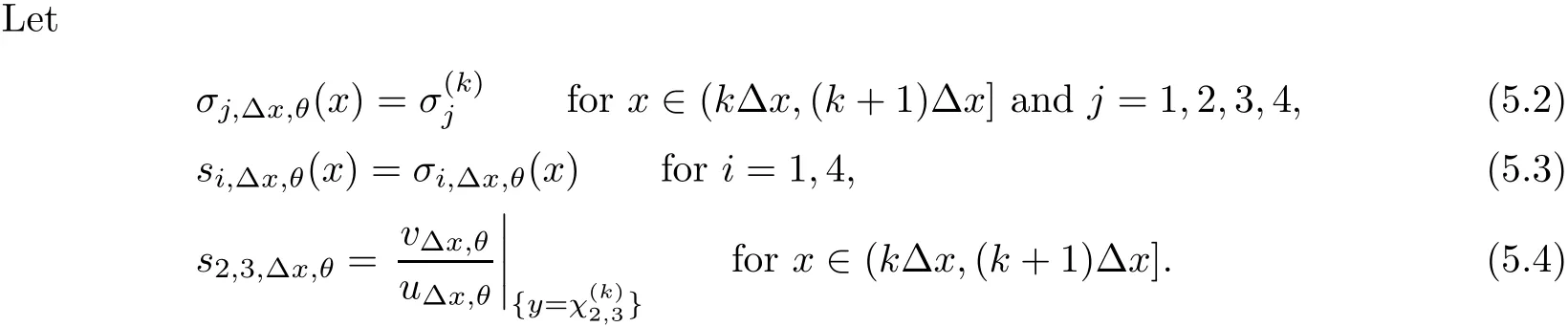
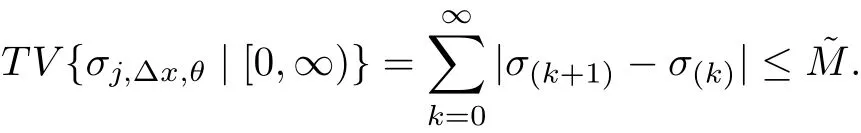


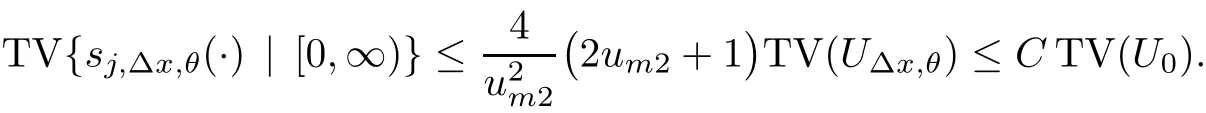
6 Global Entropy Solutions
6.1 Convergence of the Approximate Solutions


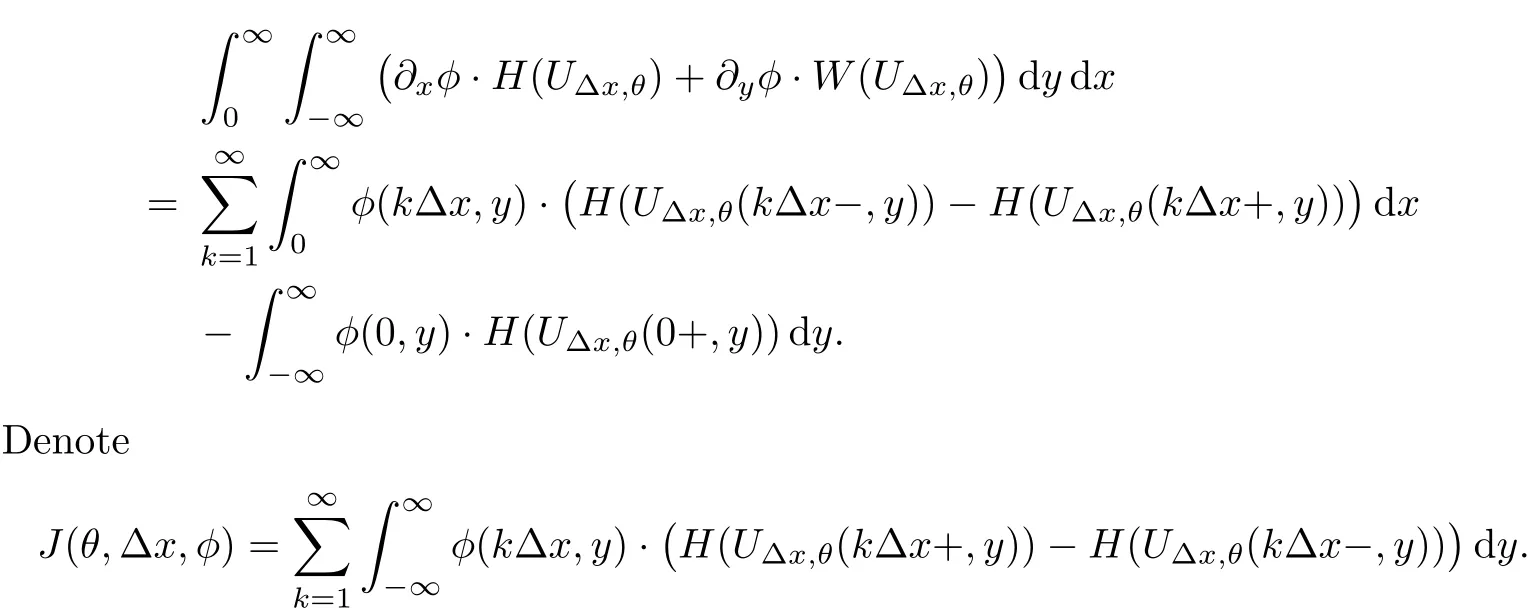




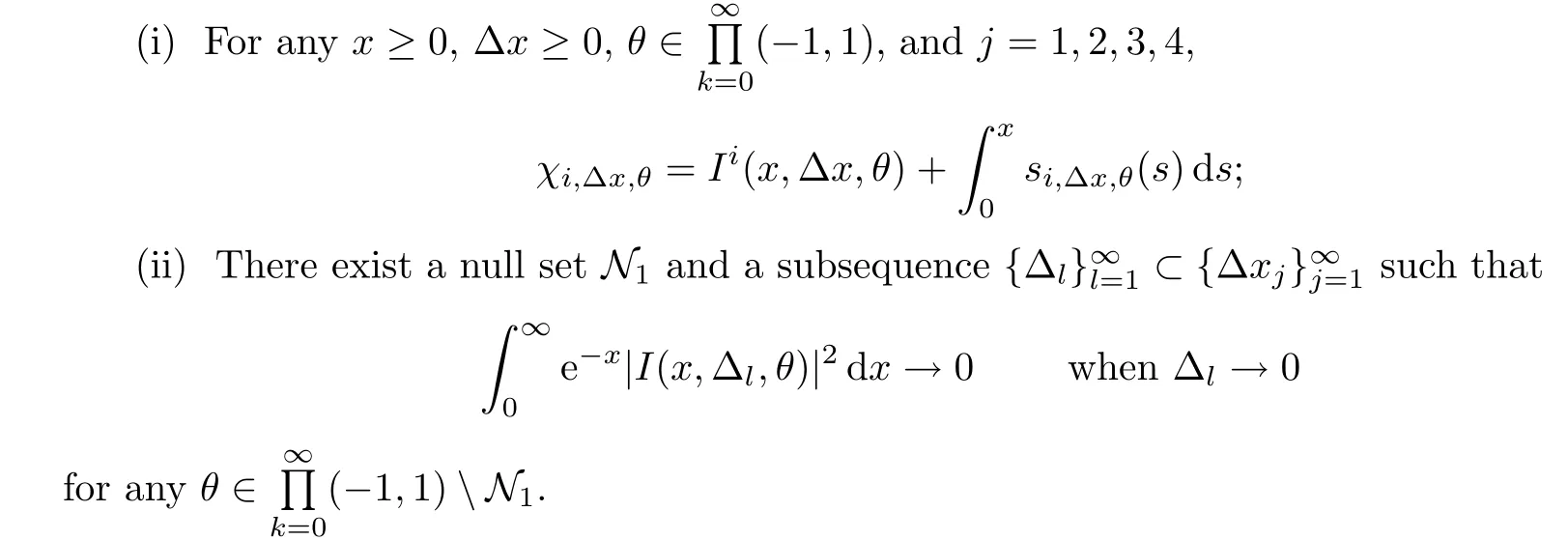
 Acta Mathematica Scientia(English Series)2018年5期
Acta Mathematica Scientia(English Series)2018年5期
