On the Coefficient Inequality for A Subclass of Starlike Mappings in Several Complex Variables
GUO Sheng-ti,XU Qing-hua
(1.College of Mathematics and Information Science,JiangXi Normal,JiangXi Normal University,Nan-Chang 330022,China;2.School of Science,Zhejiang University of Science and Technology,Hangzhou 310023,China)
§1. Introduction
Let A be the class of functions of the form:

which are analytic in the open unit disk

We denote by S the subclass of A consisting of all functions in A which are also univalent in U.Let S?denote the subclass of S consisting of the starlike functions on U.
Let X be a complex Banach space with norm k·k,X?be the dual space of X,B be the unit ball in X,Bnbe the Euclidean unit ball in Cn.Also,let?Undenote the boundary of Un,and?0Unbe the distinguished boundary of Un.
For each x∈X{0},we de fine
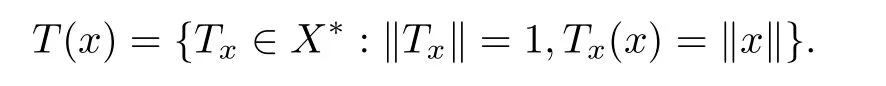
According to the Hahn-Banach theorem,T(x)is nonempty.
In[1],Fekete and Szeg? obtained the following classical result.
Let the function f(z)be de fined by(1.1).If f∈S,then
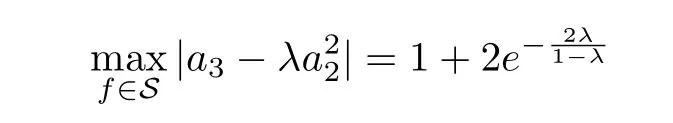
for λ∈[0,1].
The above inequality is known as the Fekete and Szeg? inequality.After that,there were many papers to consider the corresponding problems for various subclasses of the class S,and many interesting results were obtained.For example,in[9],Koepf obtained the following result for S?.
Theorem A(See[9])Let the function f(z)be de fined by(1.1).If f∈S?,then
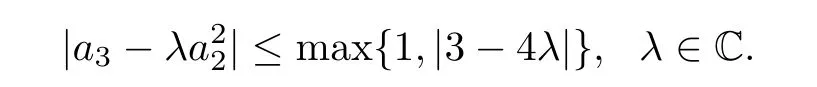
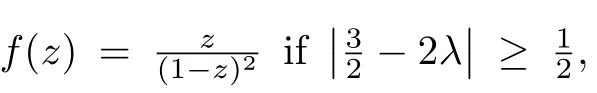
In contrast,although Fekete and Szeg? inequalities for various subclasses of the class S were established,only a few results are known for the inequalities of homogeneous expansions for subclasses of biholomorphic mappings in several complex variables.Some best-possible results concerning the coefficient estimates for subclasses of holomorphic mappings in several variables were obtained in the works of Graham,Hamada and Kohr[2],Graham et al.[3],Graham et al.[5],Hamada et al.[6],Hamada and Honda[7],Kohr[8],and Xu and Liu[14].
In[15],using some restrictive assumption,Xu and Liu extended Theorem A to the case of the class of starlike mappings de fined on the unit ball in a complex Banach space or on the unit polydisk in Cn.They first obtained the Fekete and Szeg? inequality in several complex variables.Recently,the Fekete and Szeg? inequalities are established for well-known subclasses of holomorphic mappings in several complex variables(see[16-17]).
In this paper,we establish Fekete and Szeg? inequalities for a subclass of starlike mappings de fined on the unit ball in a complex Banach space,on the unit polydisk in Cnor the bounded starlike circular domain in Cn,respectively.These results are natural extensions to higher dimensions of Theorem A.
Let H(B)denote the set of all holomorphic mappings from B into X.It is well known that if f∈H(B),then
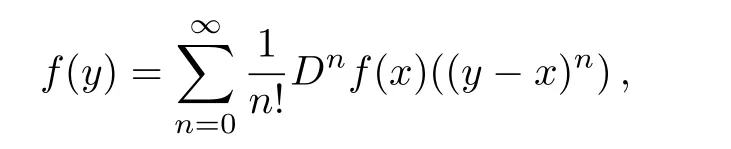
for all y in some neighborhood of x ∈ B,where Dnf(x)is the nth-Fréchet derivative of f at x,and for n≥1,
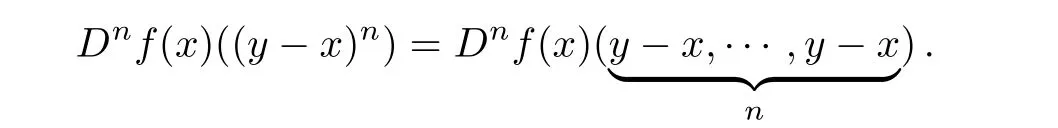
A holomorphic mapping f:B → X is said to be biholomorphic if the inverse f?1exists and is holomorphic on the open set f(B).A mapping f∈H(B)is said to be locally biholomorphic if the Fréchet derivative Df(x)has a bounded inverse for each x ∈ B.If f:B → X is a holomorphic mapping,then f is said to be normalized if f(0)=0 and Df(0)=I,where I represents the linear identity operator from X into X.
Let ? ? Cnbe a bounded starlike circular domain with 0∈ ?,and its Minkowski functional ρ(z)∈ C∞(see Lemma 2.3)except for some lower dimensional manifolds in Cn.The first Fréchet derivative and the m(m>2)-th Fréchet derivative of a mapping f ∈ H(?)at point z ∈ ? are written by Df(z),Dmf(z)(am?1,.),respectively.The matrix representations are

where
Let S?(B)(respectively,be the set of normalized starlike mappings on B(respectively,Un,?).
§2.Some Lemmas
In order to prove the desired results,we give some lemmas.
L emma 2.1[13]Let f:B→X be a normalized locally biholomorphic mapping.Then f is a starlike mapping on B if and only if
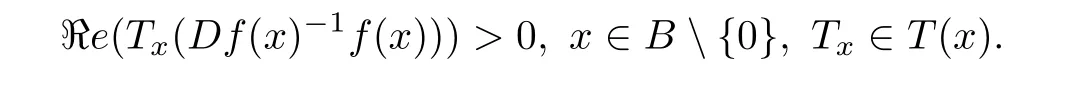
Lemma 2.2Let f:Un→Cnbe a normalized locally biholomorphic mapping.Then f ∈ S?(Un)if and only if
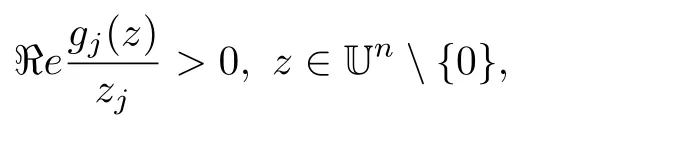
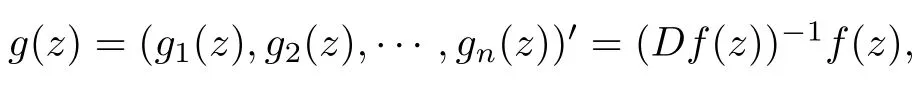
Lemma 2.3(See[10])??Cnis a bounded starlike circular domain if and only if there exists a unique real continuous function ρ :Cn?→ R,called the Minkowski functional of ?,such that
(ii)
(iii)
Furthermore,if ρ(z)(z ∈ ?)∈ C1except for some lower dimensional manifolds in Cn,then the function ρ(z)has the following properties.
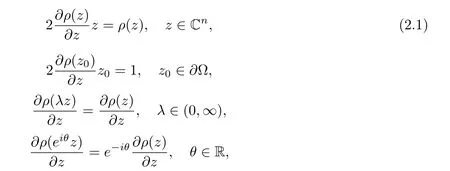
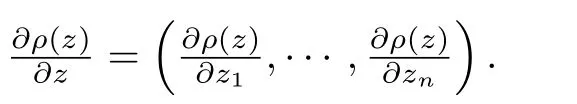
Lemma 2.4[10]Let ? ? Cnbe a bounded starlike circular domain with 0 ∈ ?,and its Minkowski functional ρ(z) ∈ C1except for some lower dimensional manifolds in Cn.Letbe a normalized locally biholomorphic mapping.Then f is a starlike mapping on? if and only if
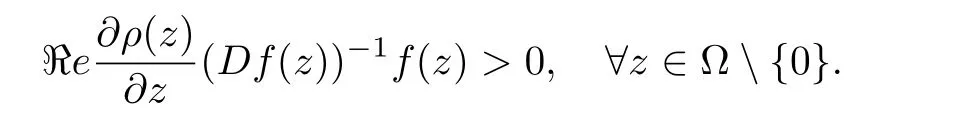
When ?=Bn,obviously,the above inequality is equivalent to the following relation.
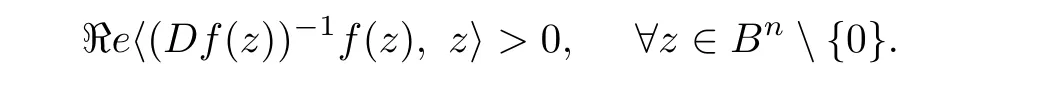
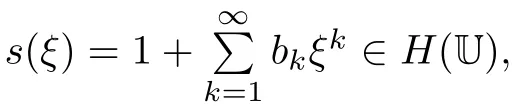
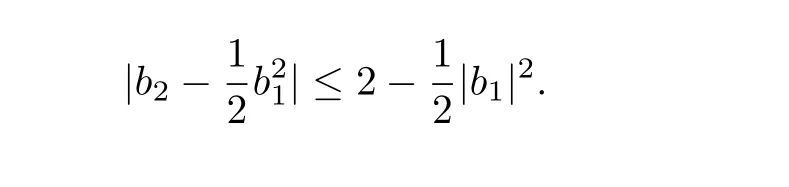
§3. Main Results
In this section,we state and prove the main results of our present investigation.
Theorem 3.1LetThen
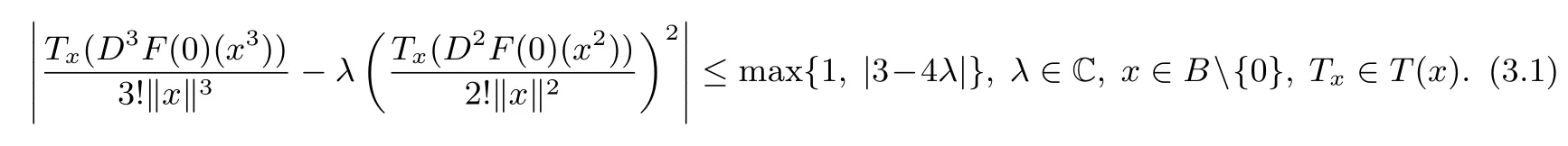
The above estimate is sharp.
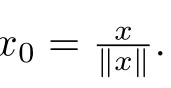
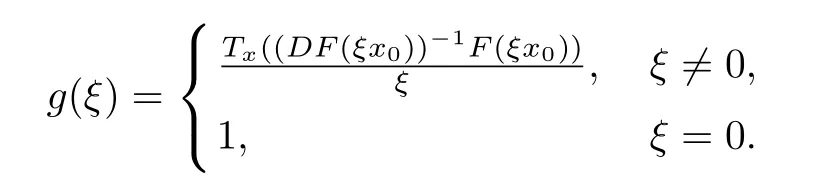
Then g∈H(U),g(0)=1,and
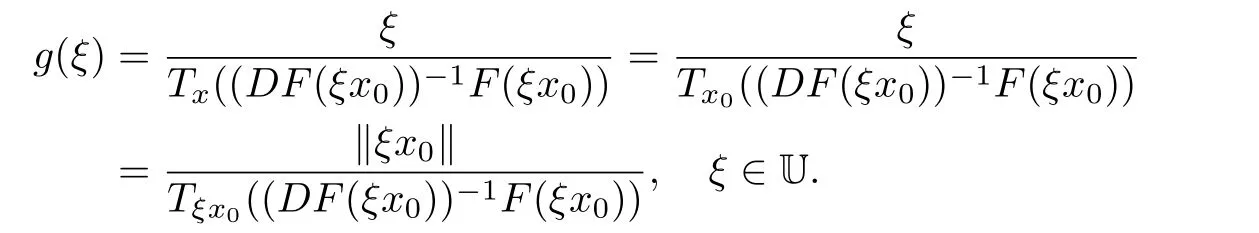
Since F ∈ S?(B),using Lemma 2.1,we obtain
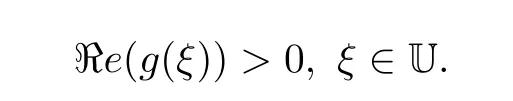
Thus,from Lemma 2.5,we have
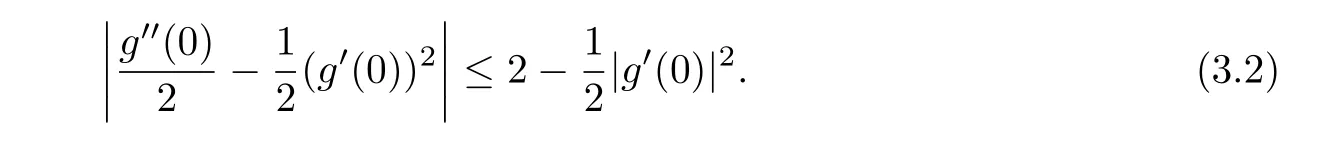
Note that F is biholomorphic on B,we get
Using a similar method as in[12](also see[4,Theorem 7.1.14]),we have
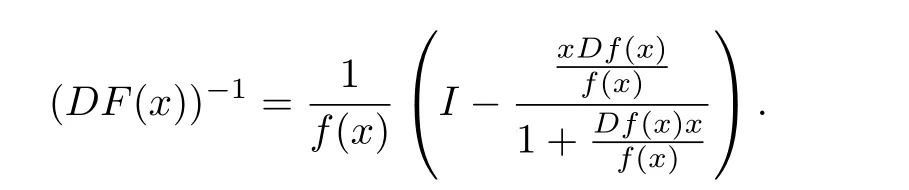
Hence,
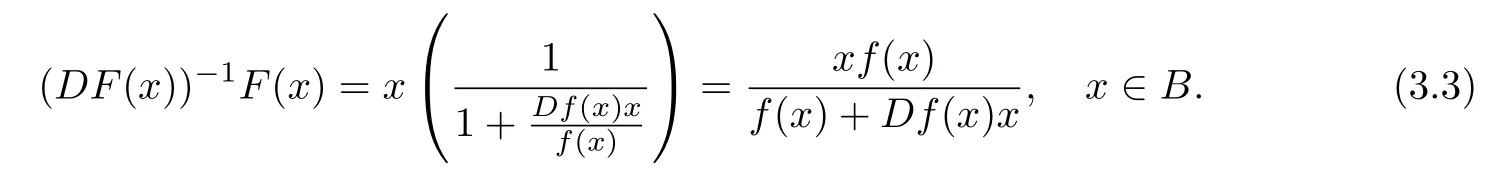
We easily compute that

In view of(3.4),we have
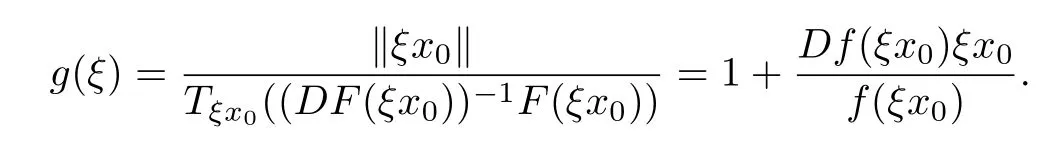
From this it follows that
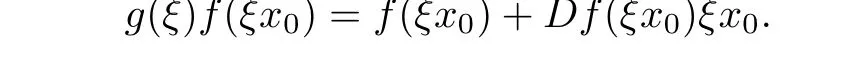
Using Taylor series expansions in ξ,we obtain

Comparing the homogeneous expansions of two sides of the above equality,we deduce that
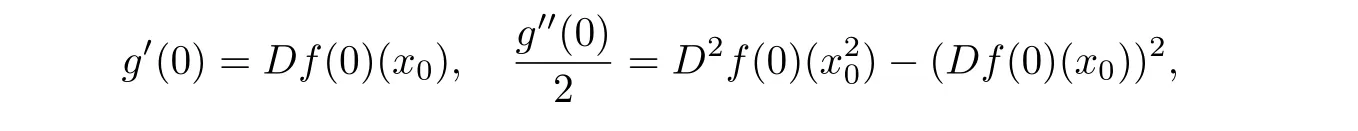
which yields the following
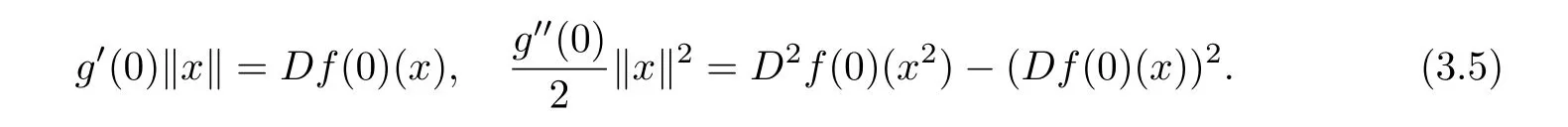
Moreover,from F(x)=xf(x),we have
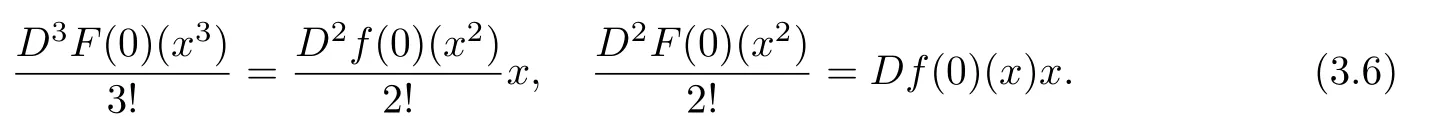
From(3.6),we conclude that
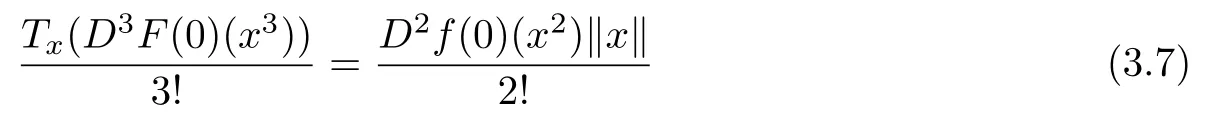
and
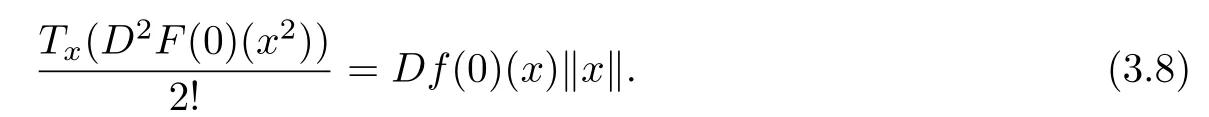
Thus,from(3.2),(3.5),(3.7)and(3.8),we have
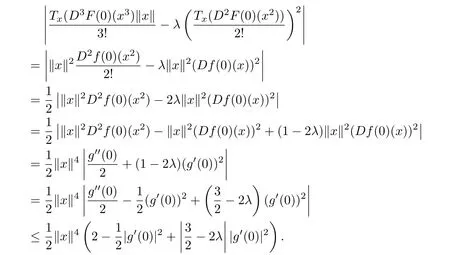
Now,we consider the following two cases.
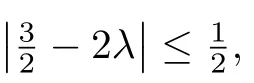
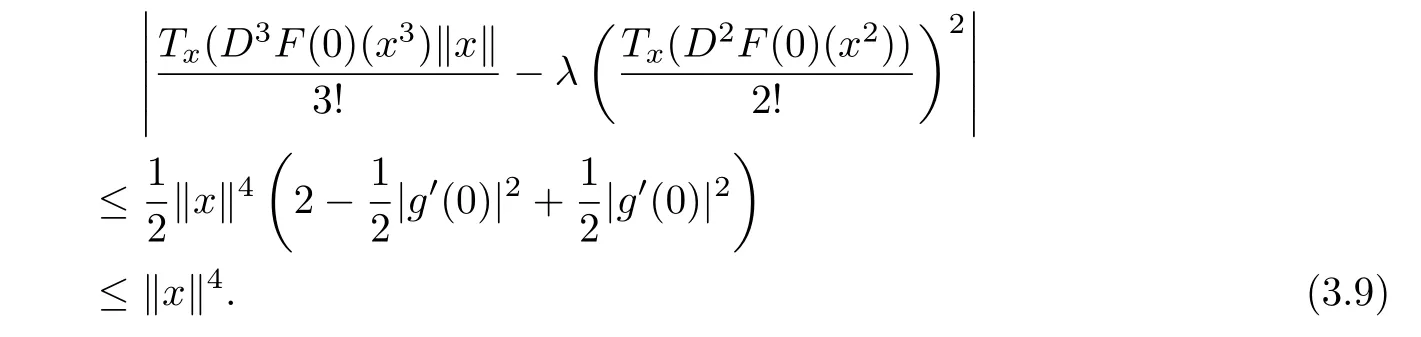
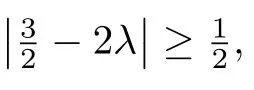
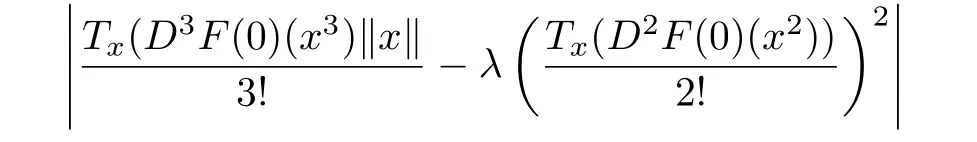
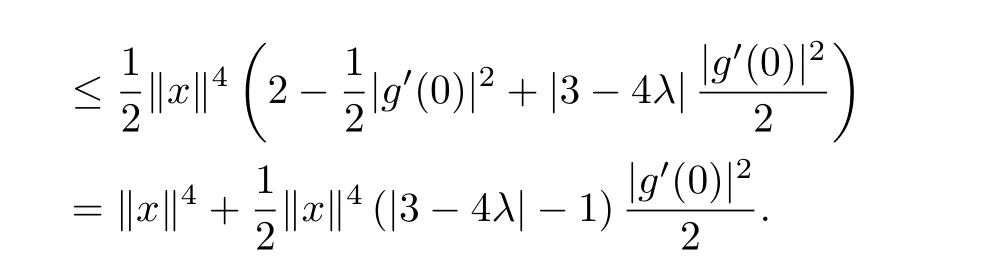
Note that|g0(0)|≤2,we obtain
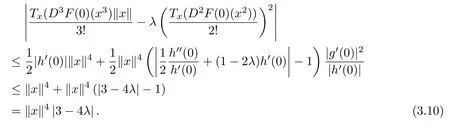
By combining(3.9)and(3.10),we get the estimate in(3.1),as desired.
To see that the estimation of Theorem 3.1 is sharp,it suffices to consider the following example.
Example 3.1Ifwe consider the following example
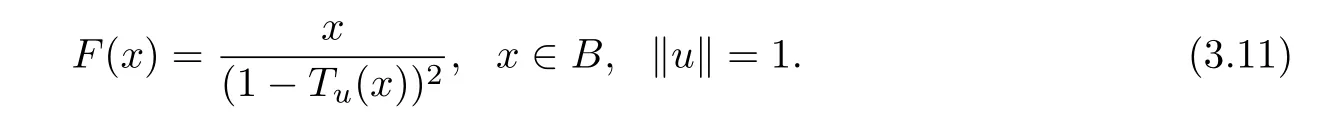
Ifwe consider the following example

Using Theorem 1 of[15],we deduce that the mappings F,de fined in(3.11)and(3.12),are in the S?(B).Taking x=ru(0 Remark 3.1When X=C,B=U,Theorem 3.1 is equivalent to Theorem A. Theorem 3.2LetThen The above estimation is sharp. ProofFor z∈Un{0},and denoteLet qj:U→C be given by Since F ∈ S?(U),from Lemma 2.2,we obtain According to(3.3),we have or,equivalently, Using Taylor series expansions in ξ,we obtain Comparing the homogeneous expansions of two sides of the above equality,we deduce that On the other hand,fromwe have Thus,from(3.13),(3.14)and(3.15),we have Using similar arguments as in the proof of Theorem 3.1,we have If z0∈ ?0Un,then we obtain Also since are holomorphic functions onin view of the maximum modulus theorem of holomorphic functions on the unit polydisc,we obtain That is Therefore as desired. In order to prove the sharpness,it suffices to consider the following example. Example 3.2If,we consider the following example Ifwe consider the following example From Theorem 3 of[15],we deduce that the mappings F,de fined in(3.16)and(3.17),are in the S?(Un).Taking z=(r,0,···,0)0(0 Remark 3.2When n=1,Theorem 3.2 reduces to Theorem A. Theorem 3.3LetThen The above estimation is sharp. ProofFix z∈ ?{0},and denote.Let p:U ?→ C be given by Then p∈ H(U),p(0)=1,and since,we deduce that Using Lemmas 2.4 and 2.5,we obtain On the other hand,we deduce from De finition 1.3 that From this it follows that F is biholomorphic on ?,and thusz∈ ?. With similar reasoning as in the proof of Theorem 3.1,we have which implies that In view of(3.20),we have From this we can conclude that Using Taylor series expansions in ξ,we obtain Comparing the homogeneous expansions of two sides of the above equality,we deduce that That is Also,sincewe have From(2.1)and(3.22),we obtain and Thus,from Lemma 2.5,(3.21),(3.23)and(3.24),we have Using similar arguments as in the proof of Theorem 3.1,we obtain The following Example 3.3 shows that the estimation of Theorem 3.3 is sharp. where r=sup{|z1|:z=(z1,0,···,0)0∈ ?}. where r=sup{|z1|:z=(z1,0,···,0)0∈ ?}. In view of(3.20),we deduce that the mappings F,de fined in(3.25)and(3.26),are in the S?(?).Taking z=Ru(0 Remark 3.3When n=1,?=U,Theorem 3.3 reduces to Theorem A. When ?=Bn,we immediately obtain the following corollary,which we merely state here without proof. Corollary 3.1Let.Then The above estimate is sharp. Remark 3.4We have just proved that the Fekete and Szeg? inequality for the subclass of starlike mappings in several complex variables.However,the corresponding problem for the general class of starlike mappings remains open.Consequently,we pose the following open problem. Open ProblemIf F ∈S?(B),then If X=Cn,B=Un,then These estimates are sharp. [1]M.Fekete,G.Szeg?,Eine Bemerkunguber ungerade schlichte Funktionen,J.Lond.Math.Soc.8(1933)85–89. [2]I.Graham,H.Hamada,G.Kohr,Parametric representation of univalent mappings in several complex variables,Canadian J.Math.54(2002)324–351 [3]I.Graham,G.Kohr,M.Kohr,Loewner chains and parametric representation in several complex variables,J.Math.Anal.Appl.281(2003)425–438. [4]I.Graham,G.Kohr,Geometric Function Theory in One and Higher Dimensions,Marcel Dekker,New York,2003. [5]I.Graham,H.Hamada,T.Honda,G.Kohr,K.H.Shon,Growth,distortion and coefficient bounds for Carathéodory families in Cnand complex Banach spaces,J.Math.Anal.Appl.416(2014)449–469. [6]H.Hamada,T.Honda,G.Kohr,Growth theorems and coefficient bounds for univalent holomorphic mappings which have parametric representation,J.Math.Anal.Appl.317(2006)302–319. [7]H.Hamada,T.Honda,Sharp growth theorems and coefficient bounds for starlike mappings in several complex variables,Chin.Ann.Math.29 B(4)(2008)353–368. [8]G.Kohr,On some best bounds for coefficients of several subclasses of biholomorphic mappings in Cn,Complex Variables.36(1998)261–284. [9]F.R.Keogh,E.P.Merkes,A coefficient inequality for certain classes of analytic functions,Proc.Am.Math.Soc.20(1969)8–12. [10]T.S.Liu,G.B.Ren,The growth theorem for starlike mappings on bounded starlike circular domains.Chin Ann of Math,19B(1998)401-408. [11]X.S.Liu,T.S.Liu,On the sharp growth,covering theorems for normalized biholomorphic mappings in Cn,Acta Math.Sci.27(B),4(2007)803–812. [12]J.A.Pfaltzgra ff,T.J.Su ff ridge,An extension theorem and linear invariant families generated by starlike maps,Ann.Univ.Mariae Curie Sklodowska,Sect.A.53(1999)193-207. [13]T.J.Su ff ridge,Starlike and convex maps in Banach spaces,Pacif.J.Math.,46(1973)575-589. [14]Q.H.Xu,T.S.Liu,On coefficient estimates for a class of holomorphic mappings,Sci China Math.52(2009)677–686. [15]Q.H.Xu,T.S.Liu,On the Fekete and Szeg? problem for the class of starlike mappings in several complex variables.Abstr.Appl.Anal.ID 807026,(2014). [16]Q.H.Xu,F.Fang,T.S.Liu,On the Fekete and Szeg? problem for starlike mappings of order α,Acta Math.Sin.(Engl.Ser.)2017,33:554-564. [17]Q.H.Xu,T.Yang,T.S.Liu,H.M.Xu,Fekete and Szeg? problem for a subclass of quasi-convex mappings in several complex variables.Front.Math.China.10(2015)1461-1472.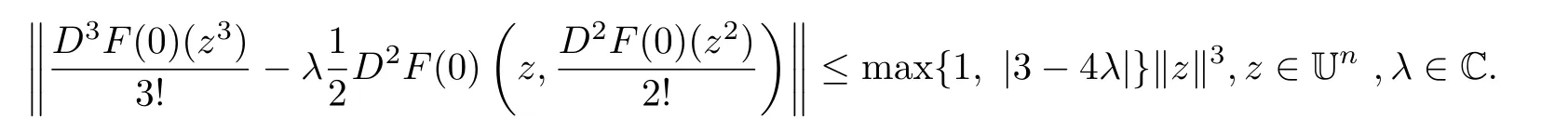
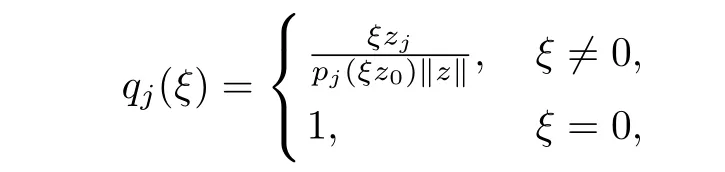
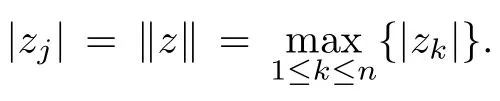
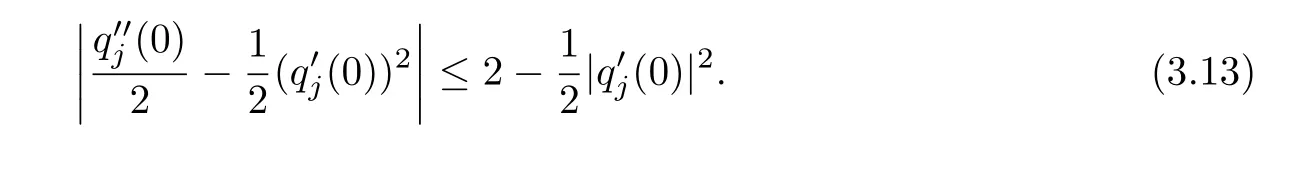
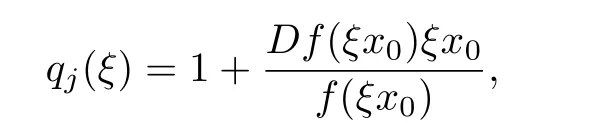
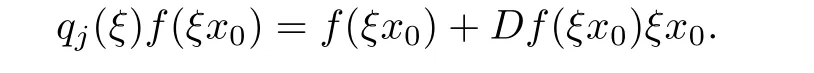
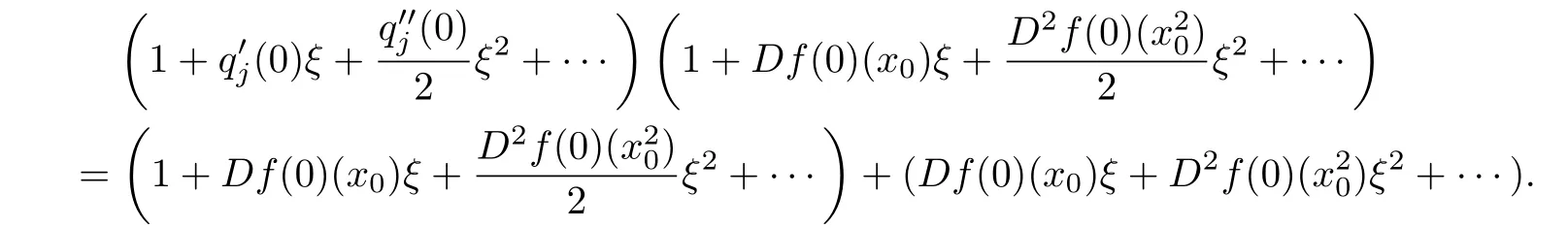
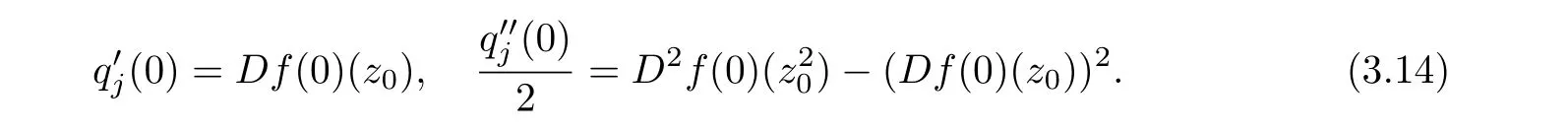
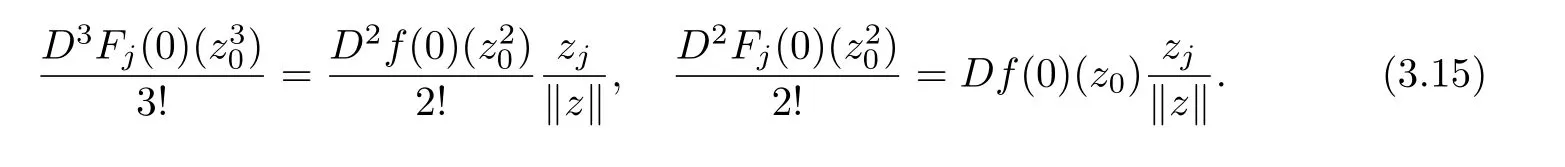
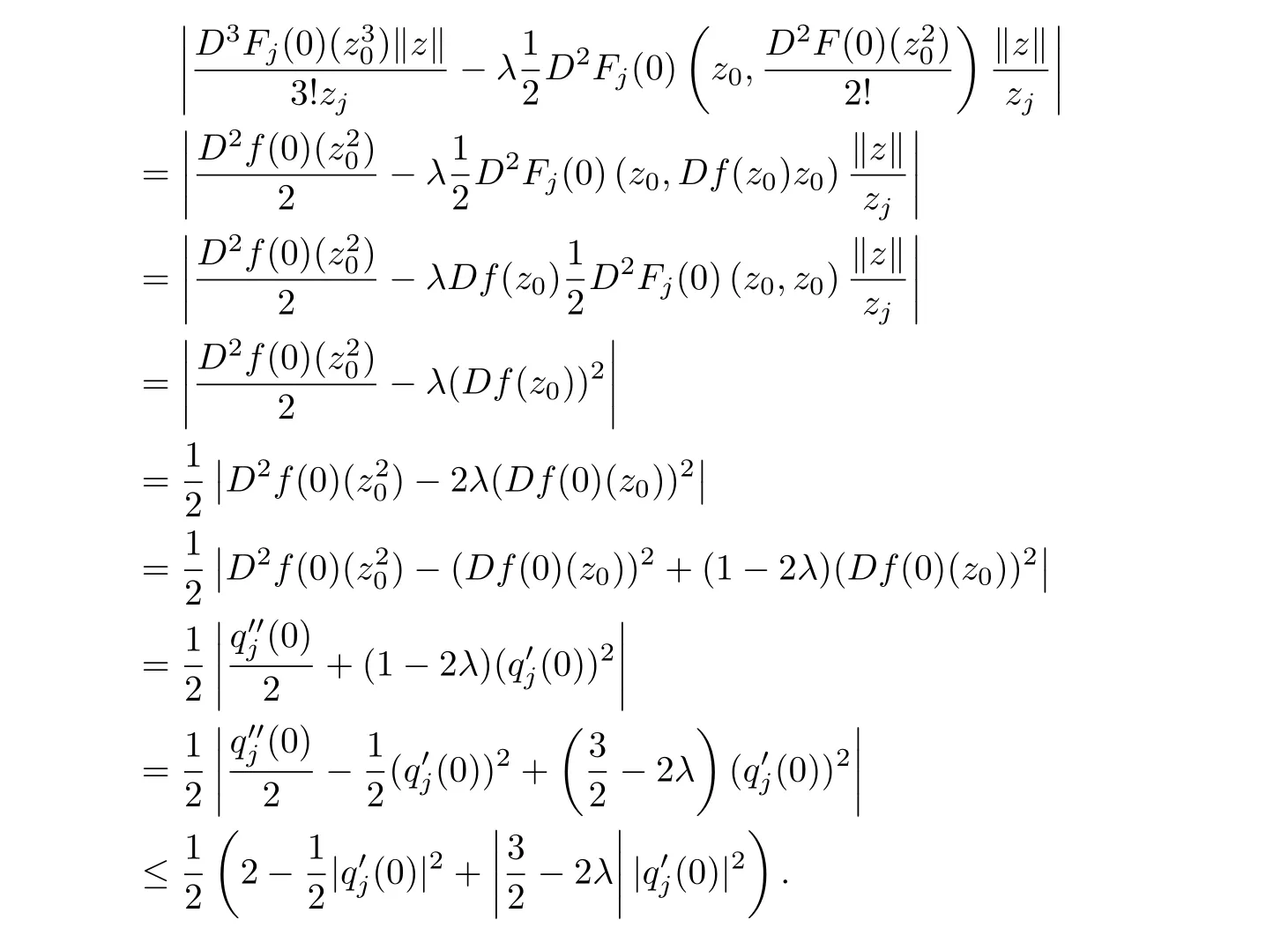
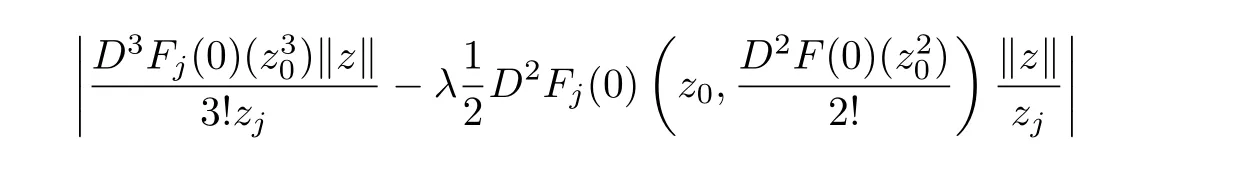
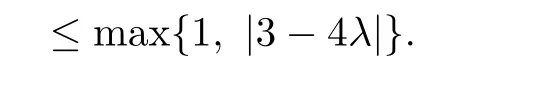
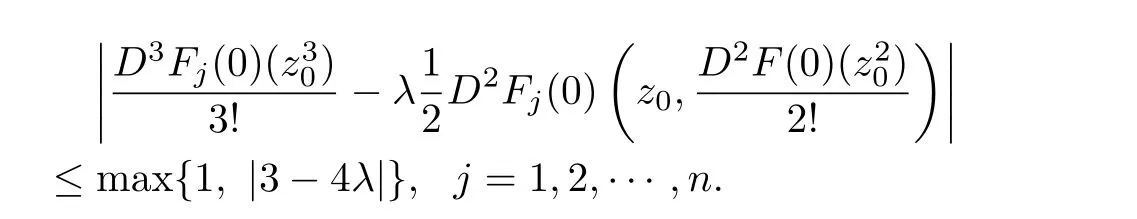
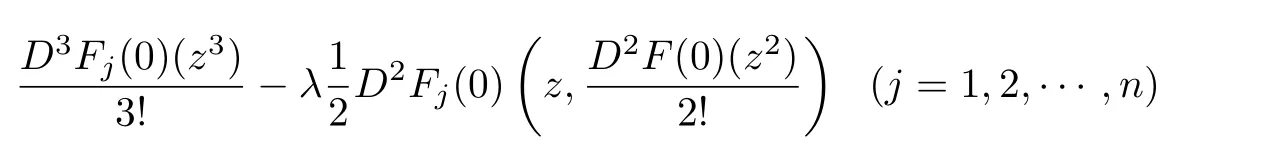
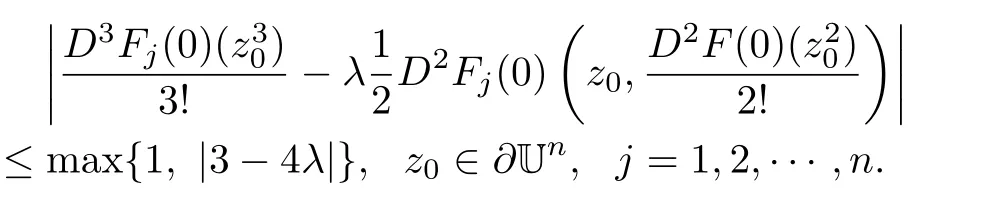
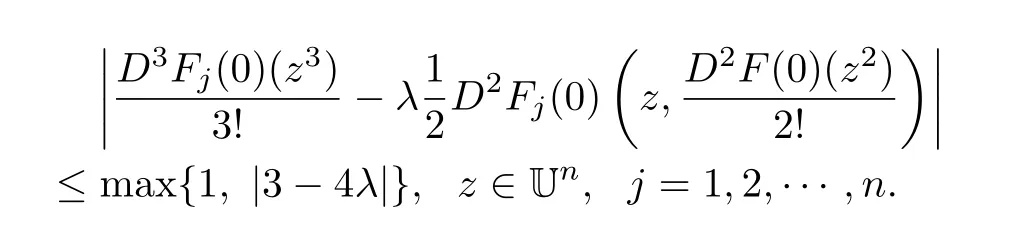
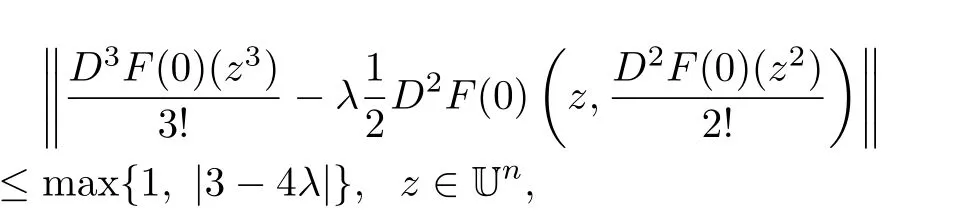
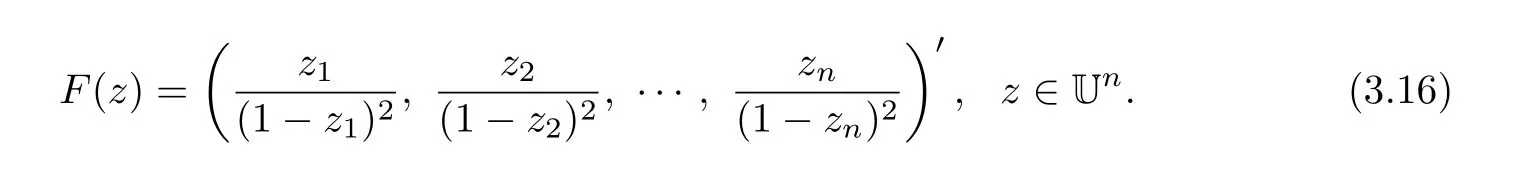
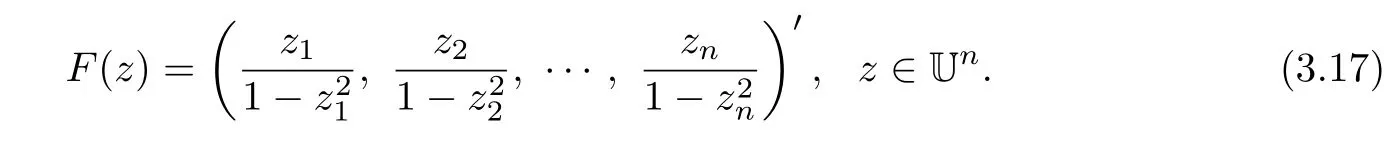
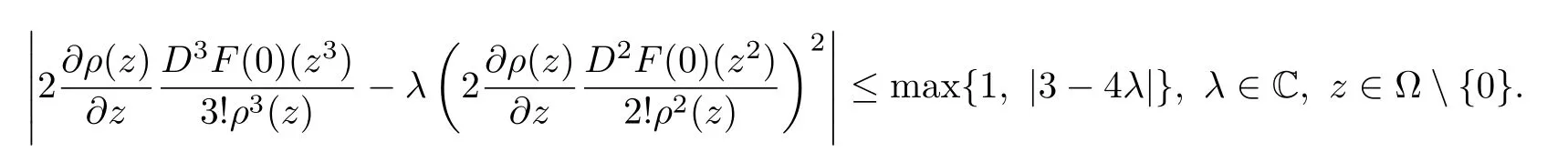
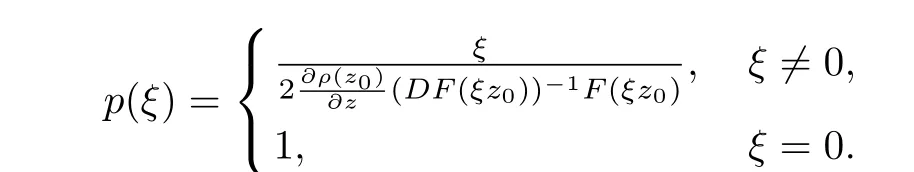
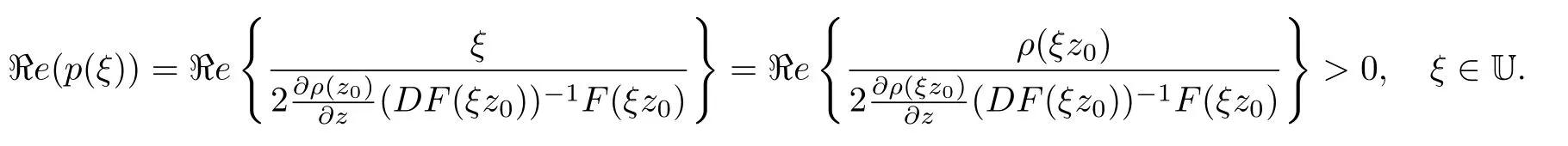
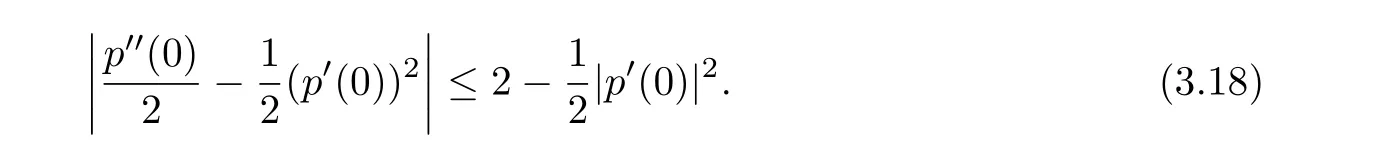
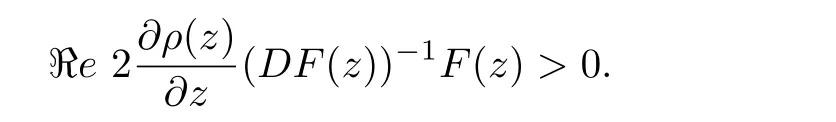
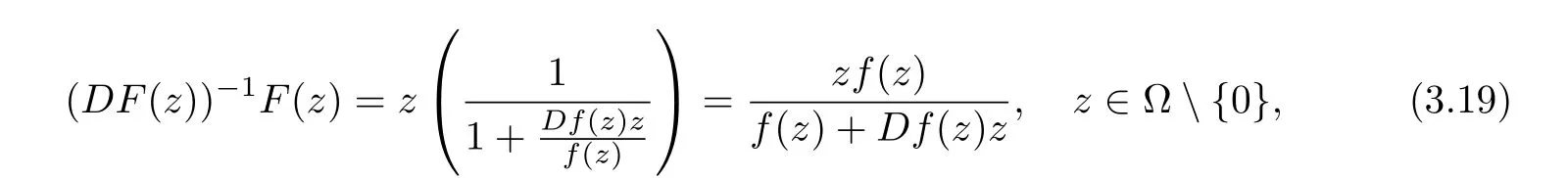
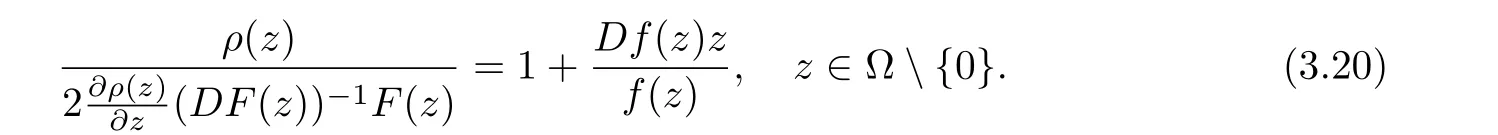


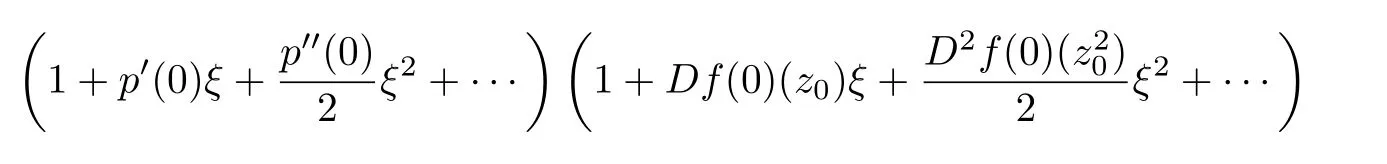
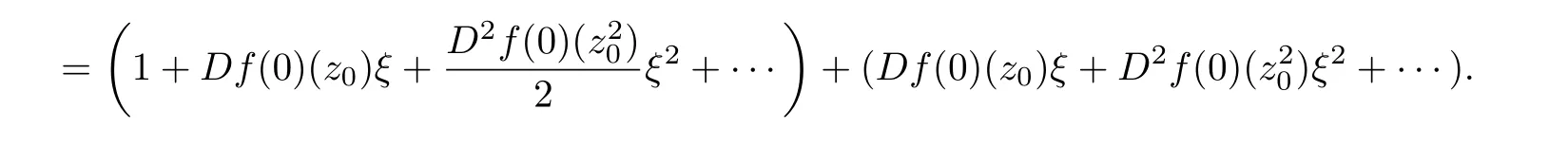


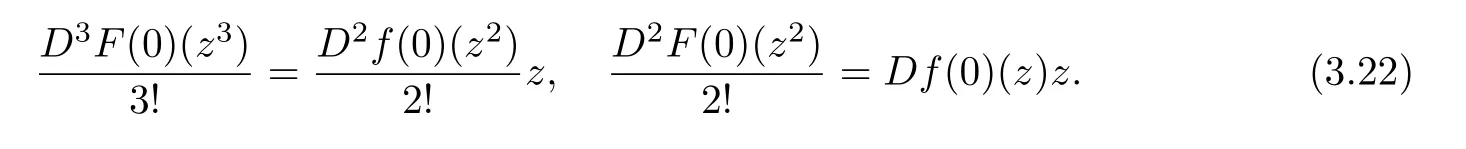
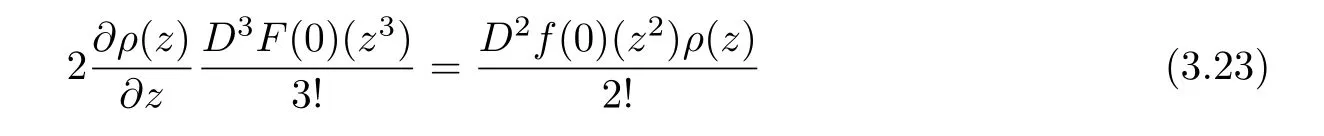
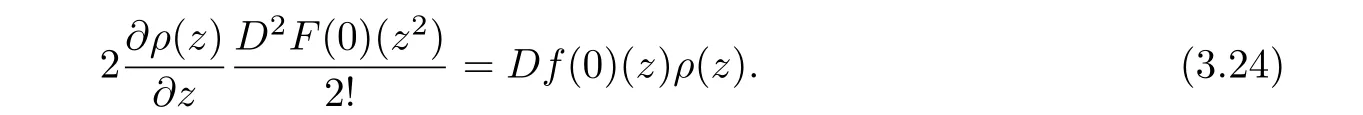

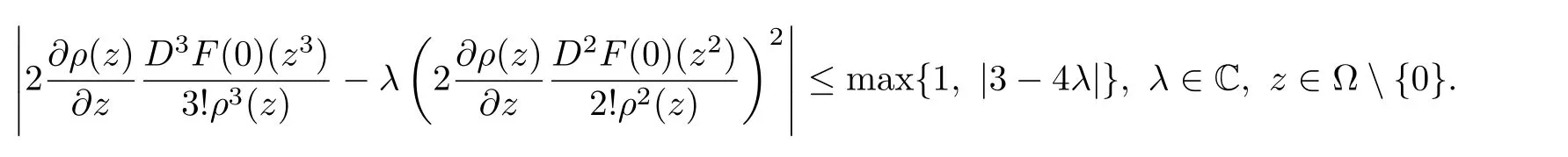
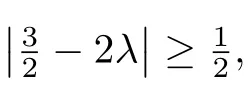

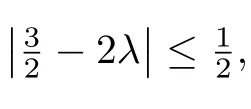

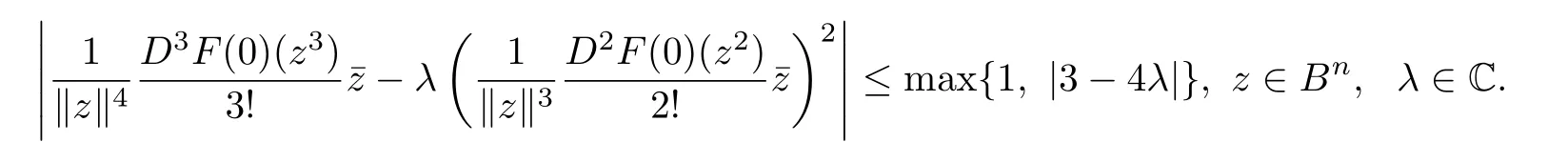
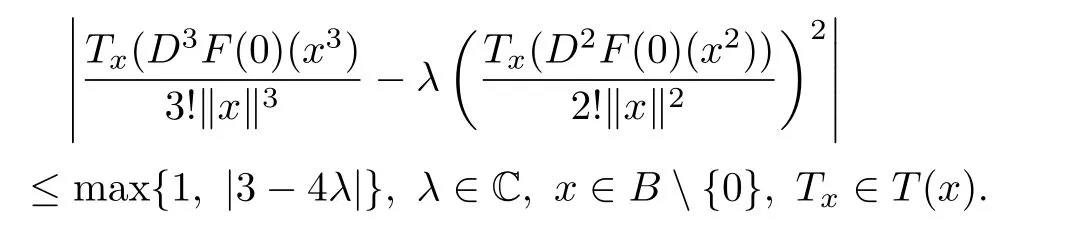
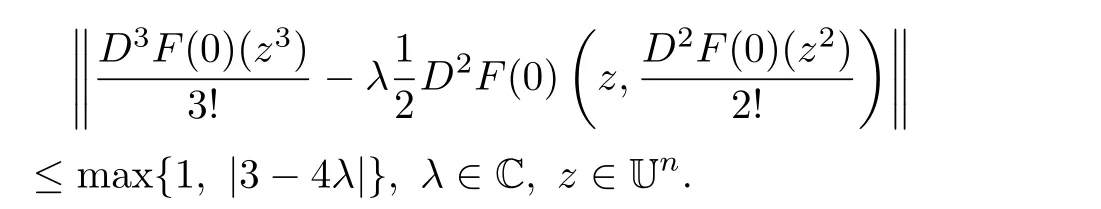
 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
