A New Method for A Rank Subtractivity Formula
(School of Mathematics and Statistics,Hubei Normal University,Huangshi,435002,China)
§1. Introduction
Throughout this paper,we denote the real m×n matrix space by Rm×n.and R(A)stand for the transpose and the range space of a given matrix A,respectively.Inrepresents the identity matrix of size n.A matrix X is called a g-inverse of A,denoted by X=A?,if it satis fies AXA=A.The collection of all possible g-inverses of A is denoted by{A?}.
Let A be an m by n matrix of rank l,and let M and N be m by k and n by q matrices,respectively,where k is not necessarily equal to q or rank to hold.This rank subtractivity formula along with the condition under which it holds is called the extended Wedderburn-Guttman theorem.The Wedderburn-Guttman theorem[5-7]: is used extensively in numerical linear algebra[8-9]as a rank reduction method,and in psychometrics[10-11],and statistics[12]as a means of extracting components which are known linear combinations of observed variables. In this note,by applying the full rank decomposition ofrank(A)=rank(F)=rank(G)=l)and the product singular value decomposition of the matrix pairsome conditions for the validity of the rank subtractivity formula(1)are obtained.Compared with the approach proposed in[2],the method in this paper is more concise and easy to perform. To begin with,we introduce two lemmas. Lemma 1(ThePSVDTheorem[13,14])Given matrices X ∈ Rk×land Y ∈ Rl×q.Then there exist orthogonal matricesand a nonsingular matrix W ∈ Rl×lsuch that where and Lemma 2(Invariance)[15]Let,and F ∈ Rp×q.Then the product DE?F does not depend on the choice of E?∈ {E?}if and only if D=0,or F=0,orand Let FG be a full rank decomposition of the matrix A∈Rm×n,that is, where F ∈ Rm×l,G ∈ Rl×n,l=rank(A)=rank(F)=rank(G).Assume thatit follows from the nonsingularity ofand,we can get By Lemma 1,we have Assume that where Z11=S?2.It follows from(6)that Thus,we can get On the other hand, By(10),we have From(9)and(11),we have proved the following result. Theorem 1Assume that FG is a full rank decomposition of the matrix A ∈ Rm×n,that is,F ∈ Rm×l,G ∈ Rl×n,l=rank(A)=rank(F)=rank(G).Letand let the product singular value decomposition ofbe given by(2).If the matrices Zij,i,j=1,2,3 are given by(7),then the relation of(1)holds if and only if Letit follows from Lemma 1 that From(12),(13)and(14),we can get Theorem 2 Letand A=FG be a full rank decomposition of the matrix A ∈ Rm×n,then the relation of(1)holds if and only if or equivalently, Applying Lemma 2,we can easily get Theorem 3 MatrixA is invariant over the choice of(MAN)?if and only ifandhold. By Lemma 1,andt1=0.If r1=0,then we have If t1=0,then we have From(7),(13),(14),(17)and(18),we can easily obtain Theorem 4The relation of(1)holds irrespective of(MAN)?if and only if rank=rankor rank(GN)=rank [1]TAKANE Y,YANAI H.On the Wedderburn-Guttman theorem[J].Linear Algebra and its Applications,2005,410:267-278. [2]TAKANE Y,YANAI H.Alternative characterizations of the extended Wedderburn-Guttman theorem[J].Linear Algebra and its Applications,2007,422(2):701-711. [3]TAKANE Y,YANAI H.On the necessary and sufficient condition for the extended Wedderburn-Guttman theorem[J].Linear Algebra and its Applications,2009,430(11):2890-2895. [4]GALáNTAI A.A note on the generalized rank reduction[J].Acta Math,Hungarica,2007,116(3):239-246. [5]GUTTMAN L.General theory and methods of matric factoring[J].Psychometrika,1944,9(1):1-16. [6]GUTTMAN L.A necessary and sufficient formula for matric factoring[J].Psychometrika,1957,22(1):79-81. [7]WEDDERBURN J H M.Lectures on Matrices[M].Colloquium Publications 17,American Mathematical Society,Providence,1934,and Dover,New York,1964. [8]CHU M T,FUNDERLIC R E,GOLUB G H.A rank-one reduction formula and its applications to matrix factorizations[J].SIAM Review,1995,37(4):512-530. [9]GALáNTAI A.Rank reduction:theory and applications[J].Internat.J.Math.,Game Theory Algebras,2003,13:173-189. [10]GUTTMAN L.Multiple group methods for common-factor analysis:their basis,computation and interpretation[J].Psychometrika,1952,17(2):209-222. [11]TAKANE Y,HUNTER M A.Constrained principal component analysis:a comprehensive theory[J].Appl.Algebra Engrg.Comm.Comput.,2001)12(5):391-419. [12]RAO C R.The use and interpretation of principal component analysis in applied research[J].Sankhyˉa A,1964,26(4):329-358. [13]DE MOOR B,ZHA H.A tree of generalizations of the ordinary singular value decomposition[J].Linear Algebra and its Applications,1991,147:469-500. [14]CHU D,DE MOOR B.On the nonuniqueness of the factorization factors in the product singular value decomposition[J].Linear Algebra and its Applications,2000,314(1):191-203. [15]GROSS J,TIAN Y.Invariance properties of a triple matrix product involving generalized inverses[J].Linear Algebra and its Applications,2006,417(1):94-107.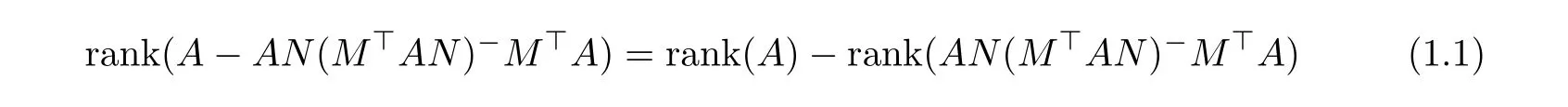

§2.Main Results


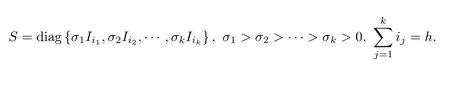

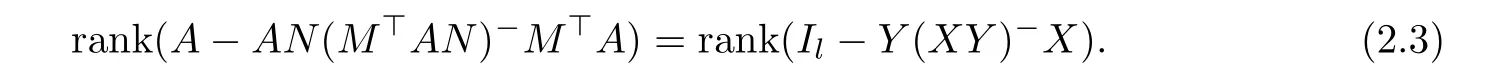

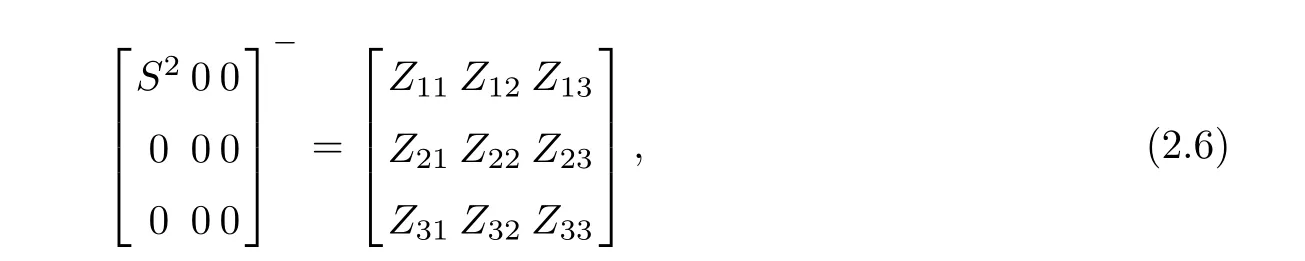



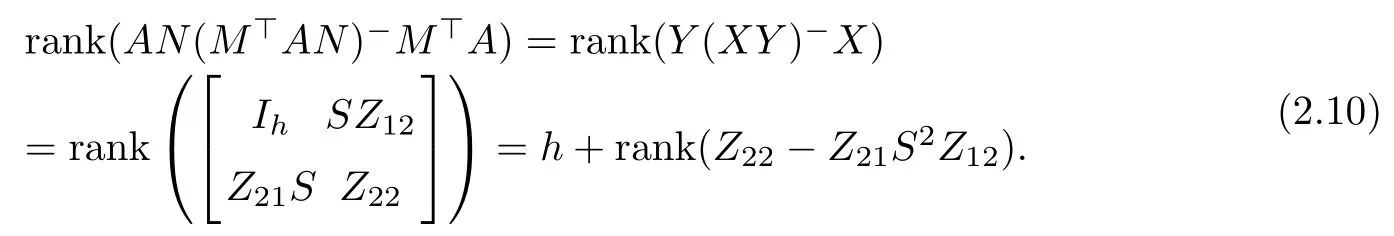





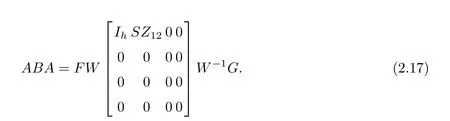
 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- On the Coefficient Inequality for A Subclass of Starlike Mappings in Several Complex Variables
- The Proof of Structural Stability of Hyperbolic Fixed Points in Ordinary Di ff erential Equations
- Strongly Ding projective modules with respect to a semidualizing module
- On Approximation by Two Kinds Modi fied Durrmeyer Rational Interpolation Operators inSpaces
- An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
- Implicative Pseudo Valuations on Hoops
