An Elliptic Gradient Estimate for A Non-homogeneous Heat Equation on Complete Noncompact Manifolds
(Nantong Normal College)
§1. Introduction
In the famous paper[1],the authors studied the Schr?dinger heat equation

on complete Riemannian manifolds with fixed metric.They proved Harnack inequalities for the solutions and got the upper bound estimates of the heat kernel.From then on,the method of gradient estimate turned out to be one of the powerful tools in the study of geometric analysis.
Let M be an n?dimensional complete Riemannian manifold.We assume that(M,g(x,t)),t∈[0,T]is a smooth solution to the Ricci flow

The study of system(1)and(2)arose from paper[1],where the author investigated the Ricci flow combined with the heat flow of harmonic maps.From then on,a large amount of work was done to understand several problems that are similar to(1)and(2)in one way or another.For instance,there are many wonderful results about the Ricci flow combined with the conjugate heat equation.We can refer to[2],where the author proved a Gaussian bound for the heat kernel of the conjugate heat equation by using gradient.In[3],the author studied the L2?preserving Schr?dinger heat flow under the Ricci flow,where the author get the existence and the uniqueness of the solutions and deduced the elliptic type gradient estimate for this evolution.Guenther established gradient estimates for positive solutions to the heat equation when the metric evolves along the Ricci flow[4].Cao study the parabolic gradient estimates for positive solutions to the equation

when the metric evolves along the Ricci flow[5].Further results in this direction can be referred from[4,5,6,7]and the references therein.
In[8],the authors got parabolic gradient estimates of the following non-homogeneous heat equation

on closed manifolds with fixed metric.On a closed manifold,the non-homogeneous heat equation(3)are closely related to the non-local heat flows which arise in geometry such that the flow preserves some Lpnorm in the sense that some geometrical quantity(such as length,area and so on)is preserved in the geometric heat flow.For more references on geometric flows such as harmonic map heat flows and non-local heat flows,one may see[8,9]and the references therein.
In this paper,we will study elliptic type gradient estimates and Harnack inequalities of(3)on complete noncompact Riemannian manifolds whose metric evolves under the Ricci flow(2).
§2.Two Lemmas
In this section we firstly give an algebraic lemma.
Lemma 2.1For every a>0,θ>0,

and

ProofWe only prove the first inequality.Let
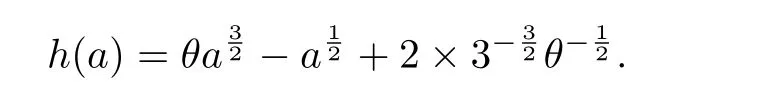
It is easy to compute that
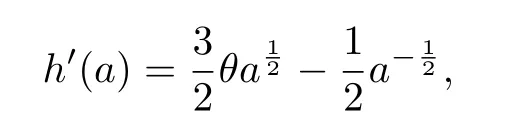
which means that

is the minimal point of h(a),but h(a0)=0.So h(a)≥0 and the lemma follows.
Let M be an n?dimensional complete noncompact manifold.We assume that(M,g(t)),t∈[0,T]is a smooth solution to the Ricci flow(2).The following lemma can help us to construct a cut-o fffunction,it has been used by many authors.For example,it was previously used in the proofs of Theorems 2.3 and 3.1 in[2];see also[10]and Chapter IV in[11].
Lemma 2.2For τ∈ (0,T],R>0,there exists a smooth function φ on[0,+∞)×[0,T],satisfying the following conditions.
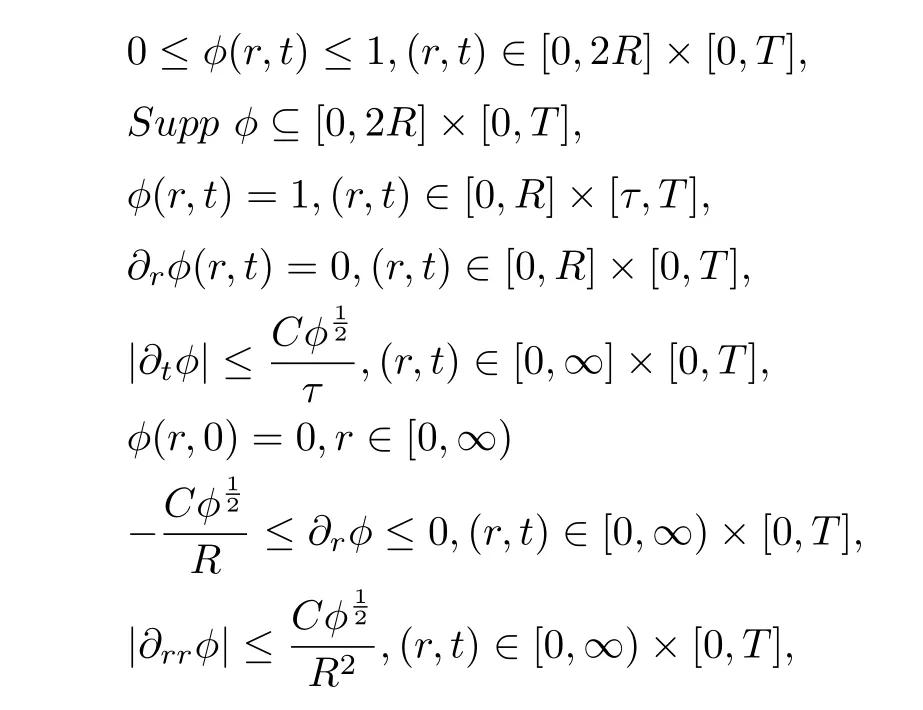
where C is a constant.
§2.Gradient Estimate
The main result in this section is the following elliptic gradient estimate for positive smooth solutions to the non-homogeneous heat equation on a complete noncompact Riemannian manifold whose metric evolves under the Ricci flow.
Theorem 3.1Let M be an n-dimensional complete Riemannian manifold,and let(M,g(x,t))t∈[0,T]be a smooth solution to the Ricci flow(2).We assume that|Ric(x,t)| ≤K2,K≥0 for all(x,t)∈B(2R,T),where
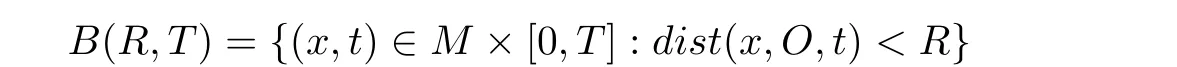
for some fixed point O.If u is a smooth solution to(3)satisfying

and
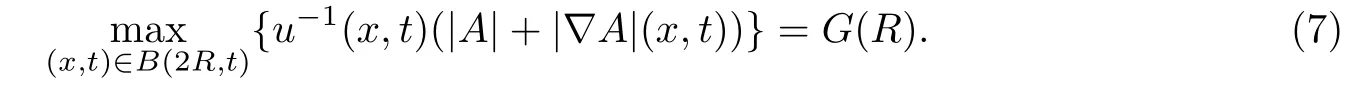
Then for all(x,t)∈B(R,T),
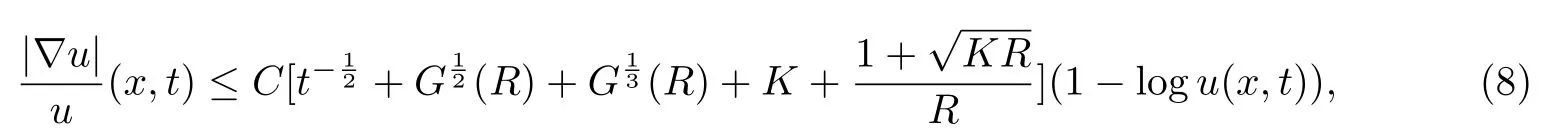
where C is a constant depending on n.
ProofWe de fine function ? onas follows,
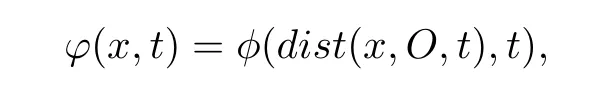
where φ is de fined on[0,+∞)×[0,T]satisfying the conditions of Lemma 2.2 for some τ∈ (0,T]and R>0.It is easy to see that ?(x,t)is supported in the closure of B(2R,T).
Let logu=f,then(3)can be rewritten as
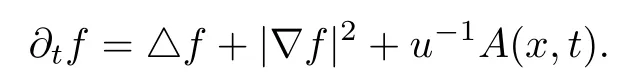
Let
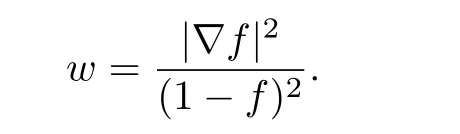
By the fact that
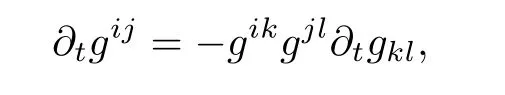
we can compute as,
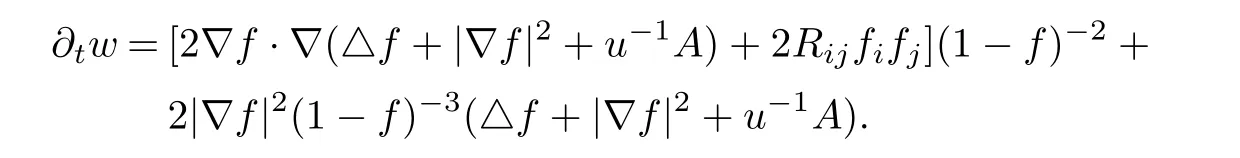
Hence
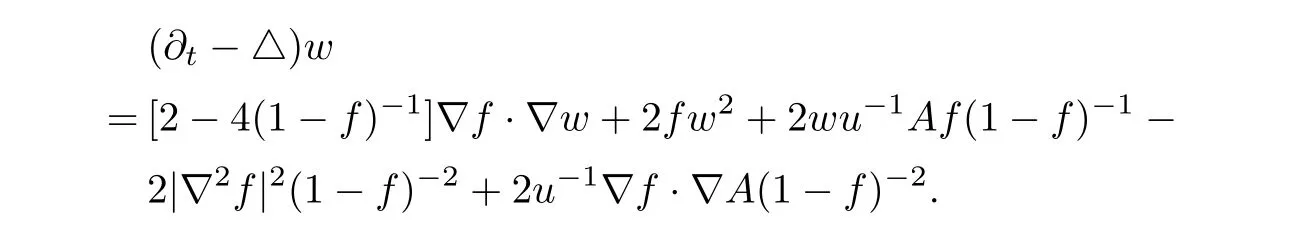
Let(x0,t0)be the maximal point of ?w on B(2R,τ).Notice that ?(x,t)is smooth at(x,t)wheneverand x is not in the cut locus of O with respect to the metric g(x,t).But,as in[11],a classical discussion shows that we can assume that x0is outside of the cut locus of O.Then ator

and
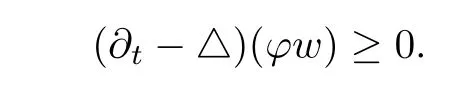
We then get that at(x0,t0),
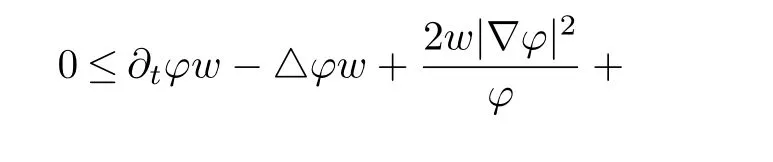
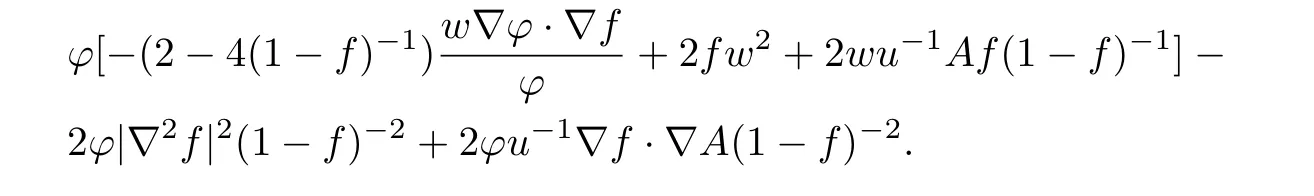
It is easy to see
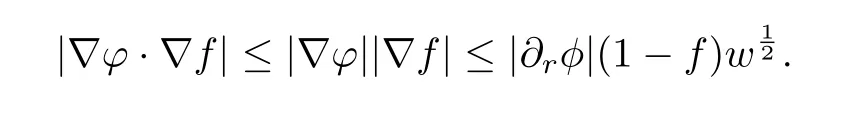
We also note
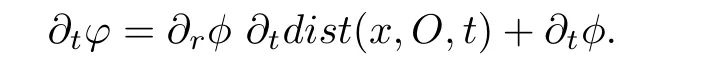
By Lemma 8.28 in[12],we have

where Ric denotes the Ricci curvature of g(x,t0),the supremum is take over all the minimal geodesic γ(s)with respect to g(x,t0),that connect x0to O and are parametrized by arclength.Hence
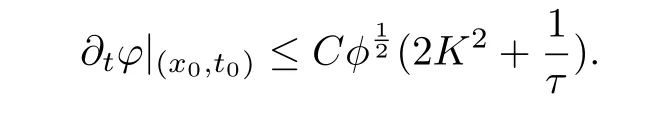
The Laplacian comparison theorem tells us that
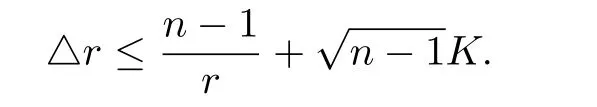
Hence,
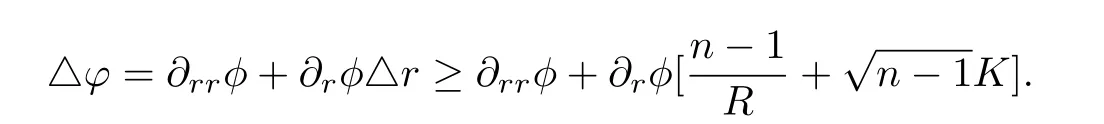
Hence
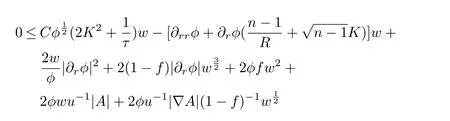
holds at(x0,t0).By Lemma 2.2 and the fact that 1?f≤?2f,we conclude that at(x0,t0),
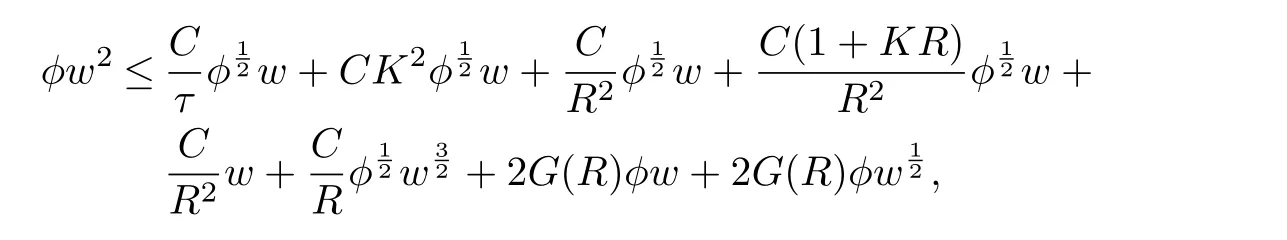
where and the following we use the same symbol C for possibly di ff erent constants.Note that 0≤φ≤1,we conclude that at(x0,t0),
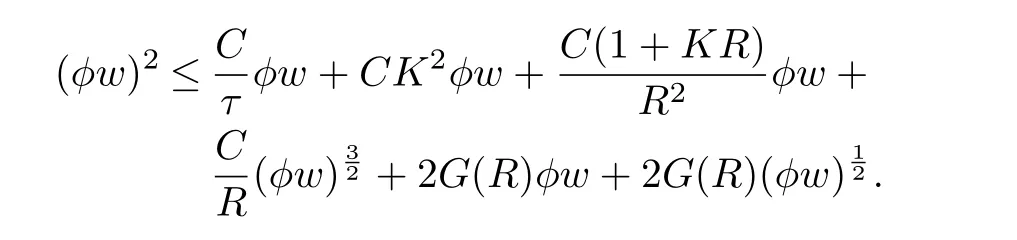
Choose
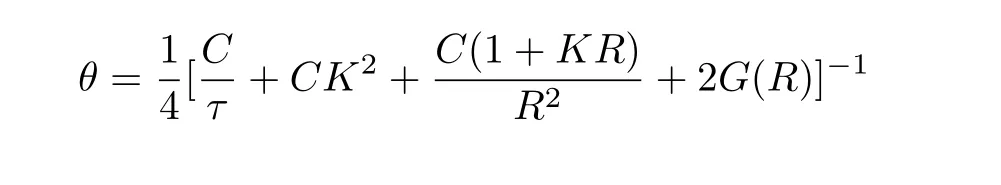
andin the two inequalities of Lemma 2.1 respectively,we get
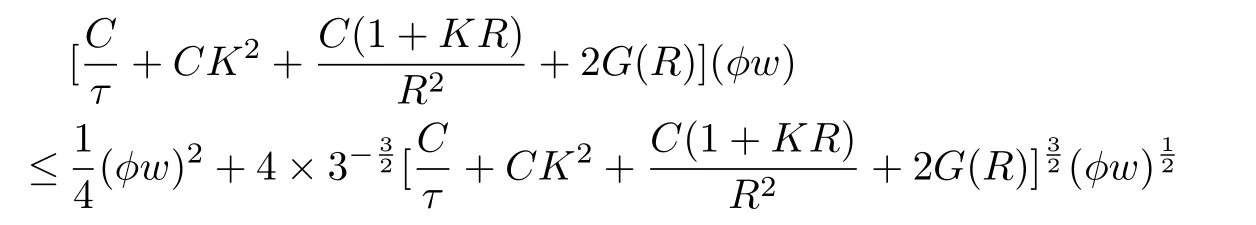
and
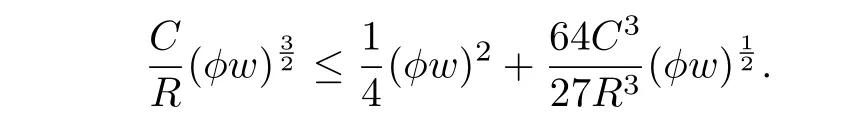
By the fact that
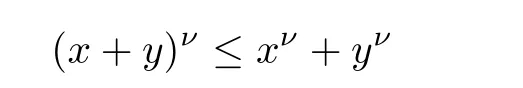
for all x>0,y>0,0<ν<1,we conclude that
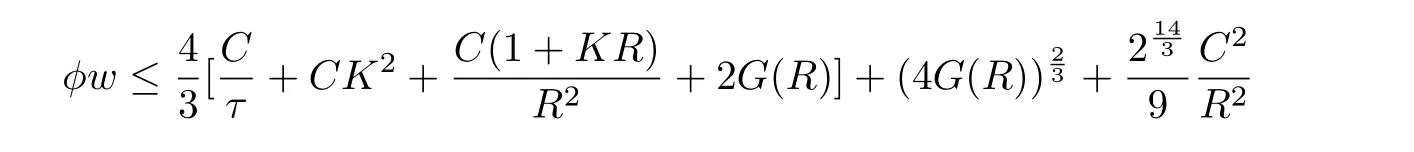
holds at(x0,t0).So for every x ∈ M,such that dist(x,O,τ) Then Theorem 3.1 follows for the reason that τ∈(0,T]is arbitrarily. Letting R→∞in Theorem 3.1,we get a global gradient estimate for positive smooth solutions to the non-homogeneous heat equation on a complete noncompact Riemannian manifold whose metric evolves under the Ricci flow. Corollary 3.2Let M be an n-dimensional complete Riemannian manifold,and letbe a solution to the Ricci flow(2).We assume that|Ric(x,t)|≤ K2,K ≥ 0 for all(x,t)∈M×[0,T].If u is a smooth solution to(3)satisfying(6)and Then for all(x,t)∈M×[0,T], where C is a constant depending on n. Based on the gradient estimate established in Theorem 3.1,we can derive the following Harnack inequality,which can be used to compare solutions at the same time. Theorem 4.1Let M be an n-dimensional complete Riemannian manifold,and let(M,g(x,t))t∈[0,T]be a solution to the Ricci flow(2).We assume that|Ric(x,t)|≤ K2,K ≥ 0 for all(x,t)∈M×[0,T].If u is a smooth solution to(3)satisfying(6)and(9).Then for x1,x2∈M,t∈[0,T], where r(x1,x2)denotes the geodesic distance between x1,x2,and with C given in Corollary 3.2. ProofLet’s consider the minimal geodesic γ(s):[0,1]→ M,so thatby(10), This inequality implies(11). [1]HAMILTON R S.The formation of singularities in the Ricci flow,Surveys in di ff erential geometry,Vol.II,Int.Press,Cambridge,MA,1995:7-136. [2]ZHANG Q.Some gradient estimates for the heat equation on domains and for an equation by Perelman[J].International Mathematics Research Notices,2006:39. [3]WANG L F.L2-preserving Schr?dinger heat flow under the Ricci flow[J].Balkan Journal of Geometry and its Applications,2010,15(2):121-133. [4]GUENTHER C.The fundamental solution on manifolds with time-dependent metrics[J].Journal of geometric analysis,2002,12:425-436. [5]CAO X D.Di ff erential Harnack estimates for backward heat equations with potentials under the Ricci flow[J].Journal of Functional Analysis,2008,255(4):1024-1038. [6]ABOLARINWA A.Gradient estimates for heat-type equations on manifolds evolving by the Ricci flow[J].International Journal of Pure and Applied Mathematics,2014,93(3):463-489. [7]BAILESTEANU M,CAO X,PULEMOTOV A.Gradient estimates for the heat equation under the Ricci lf ow[J].Journal of Functional Analysis,2010,258:3517-3542. [8]MA L,CHENG L.Non-Local heat flows and gradient estimates on closed manifolds[J].Journal of Evolution Equation,2009,9(4):789-807. [9]AUBIN T.Some nonlinear problems in Riemannian geometry[M].Springer-Verlag,Berlin,1998. [10]SOUPLET P,ZHANG Q.Sharp gradient estimate and Yau’s Liouville theorem for the heat equation on noncompact manifolds[J].Bulletin London Mathematical Society,2006,38:1045-1053. [11]SCHEON R,YAU S T.Lectures on di ff erential geometry[M].Cambridge,MA:International Press,1994. [12]CHOW B,CHU S C,GLICKENSTEIN D,GUENTHER C,ISENBERG J,IVEY T,KNOPF D,LU P,LUO F,NI L.The Ricci flow:techniques and applications.Part I.Geometric aspects[M].American Mathematical Society,Providence,RI,2007.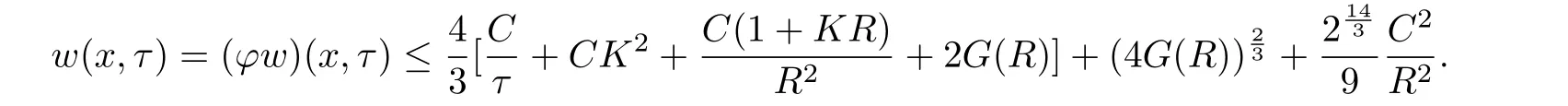
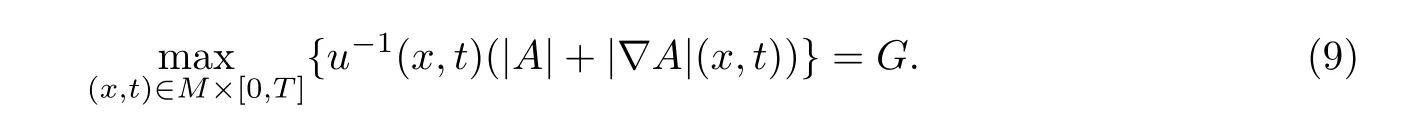
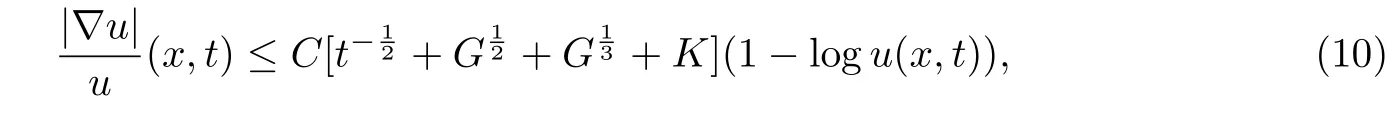
§2. Harnack Inequality
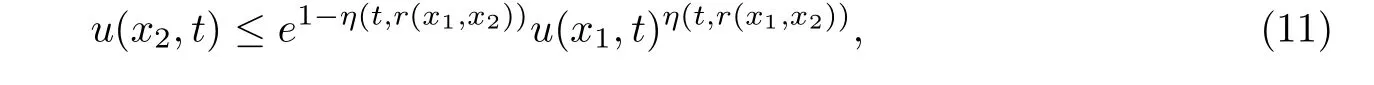
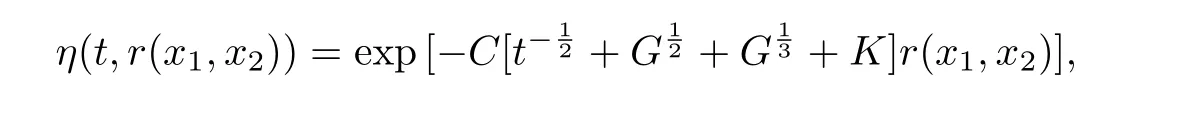
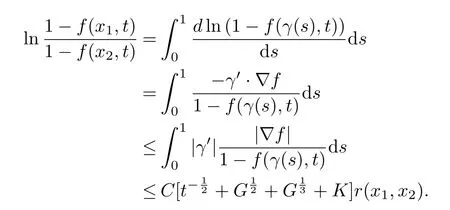
 Chinese Quarterly Journal of Mathematics2018年1期
Chinese Quarterly Journal of Mathematics2018年1期
- Chinese Quarterly Journal of Mathematics的其它文章
- On the Coefficient Inequality for A Subclass of Starlike Mappings in Several Complex Variables
- The Proof of Structural Stability of Hyperbolic Fixed Points in Ordinary Di ff erential Equations
- Strongly Ding projective modules with respect to a semidualizing module
- On Approximation by Two Kinds Modi fied Durrmeyer Rational Interpolation Operators inSpaces
- A New Method for A Rank Subtractivity Formula
- Implicative Pseudo Valuations on Hoops
