(School of Mathematics and Statistics Henan University,Kaifeng 457000,P.R.China)

§1. Structural Stability of Hyperbolic Fixed Points

Consider the following nonlinear systems

and it’s perturbed system

where x:R→Rnand f,η∈C1(Rn,Rn).

Theorem 1.1Suppose thatis a hyperbolic fixed point of the nonlinear system(1.1),such that η(0)=0.If kηkC1is sufficiently small,then there is an open setand a homeomorphismsuch that where ?t(x)and ψt(x)are the flows of systems(1.1)and(1.2).That is to say the hyperbolic fixed point is Structural stable.

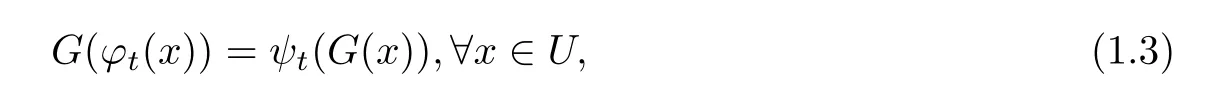
In[2],they gave the above theorem,but the proof has some mistake,they said that(1.1)and(1.2)have the same linearized system when the norm kηkCris small enough.For example,if the perturbed term η(x)= εx for ε>0 and small enough,then(1.1)and(1.2)do not have the same linearized system and Hartman Theorem can not be used directly as claimed in[2].In this paper,we will correct their proof of this theorem by using the idea of Hartman Theorem.

§2. The proof of Theorem 1.1

Our proof falls into the following four steps.

Firstly,according to the proof of Hartman-Grobman’s theorem in[1],we only need to prove that this theorem holds for linear perturbations of linearized systems.

Without loss of generality,let ζ=0.By Theorem 4.8 of[1],there is an open subset U1? Rnand a homeomorphism G1:U1→G1(U1)such that

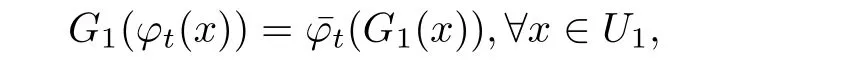
whereis the flow at zero point of linearized system(1.1).Similarly,there is an open subset U2and a homeomorphism G2?U2such that

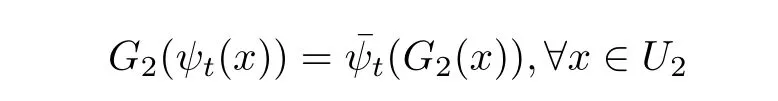
whereis the flow at zero point of linearized system(1.2).If there is an open subset U and a homeomorphism G:U→G(U)such that

Then let,we will have

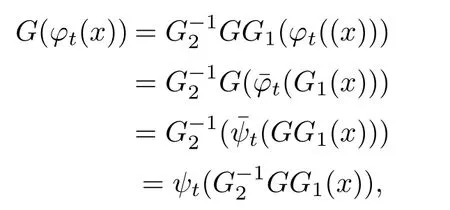
thenis the homeomorphism we want to show.Therefore,it is only necessary to prove the theorem to the linear system.

Secondly,we will prove there is a map G:Rn→Rnfor time-one flow,satis fied(1.3).Consider the linearized systems at zero point of system(1.1)and(1.2)

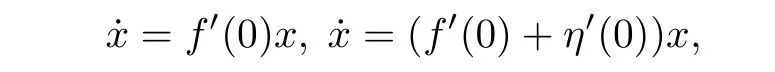
Their flows are

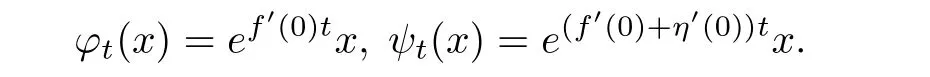
De fine A= ?1(·),then A is a hyperbolic linear transformation.De fine an appropriate bump function γ∈C1(Rn→[0,1])on a neighborhood of the origin

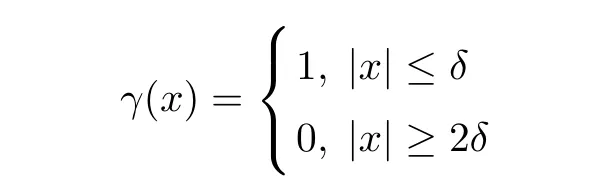
with δ>0 small enough.Consider the di ff erential equation

(i)The function f?:Rn→Rnhas a finite Lipschitz constant.

(ii)There is an open neighborhood V of the origin such thatagrees with ψ1on V.

(iii)The function p(x):=F(x)? Ax has finite C1-norm that is sufficiently small when kηkC1is small enough,by Lemma 4.7 in[1],there is a function h,h∈C(Rn),h(0)=0,khk<1,and

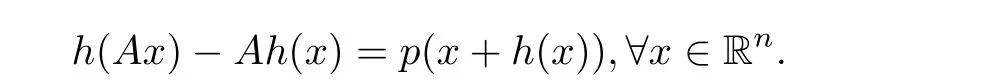
by Lemma 4.9 in[1],when the C1-norm of p is sufficiently small,there is a function g∈C(Rn)such that Ag(x)?g(F(x))=p(x).By de fining G(x):=x+g(x),we have that

Thirdly,we will show that the mapping G satis fies the equation(1.3)for any flow at any time.De fine G:Rn→Rn

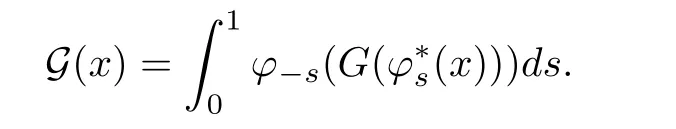
We will show that

In fact,let τ=s+t? 1,from(2.2),we have

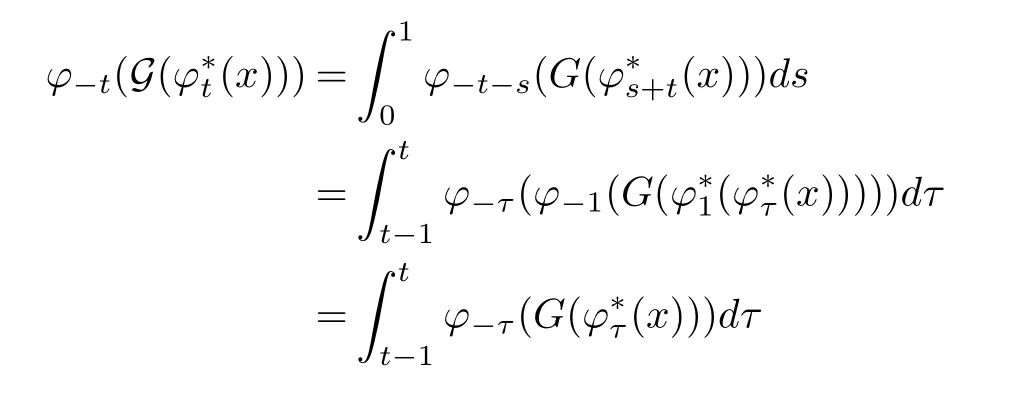
By splitting the last integral into the two parts

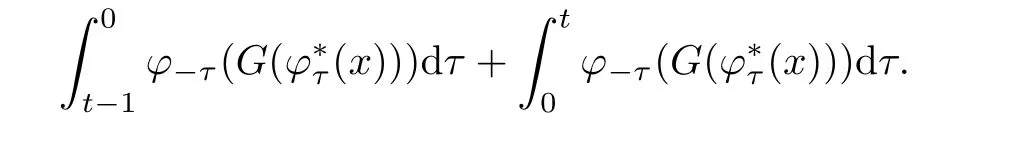
Let σ = τ+1 in the first integral,from(2.2),we obtain the identity

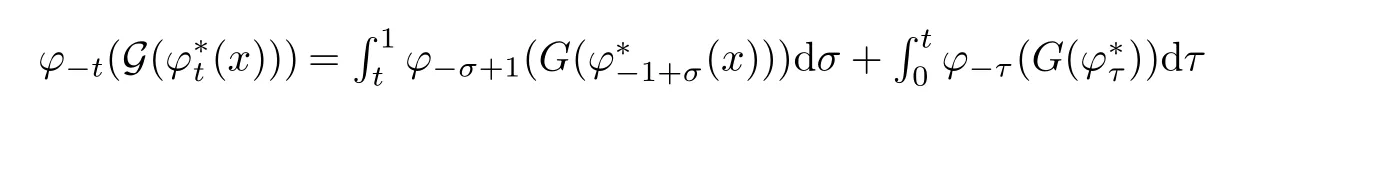
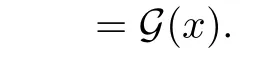
Then we will proof

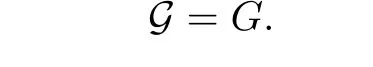
If we set t=1 in equation(2.3)and recall equation(2.2),we have the functional identities

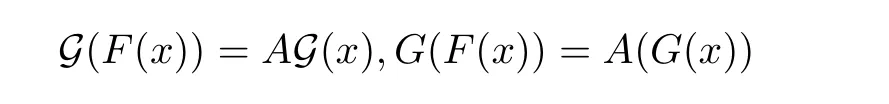
By Lemma 4.9 of[1],the function G which satis fies the same functional equation is unique among all continuous transformations with the form G(x)=x+g(x),g∈C(Rn).Thus,in order to prove G=G,it suffices to show that the function G(x)?x∈C(Rn).Here we only need to prove that G(x)?x is bounded on Rn.Let us note that we have the identities

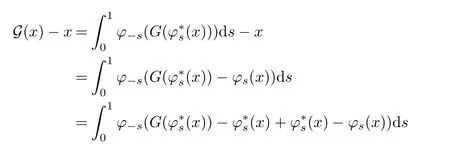
and the estimate

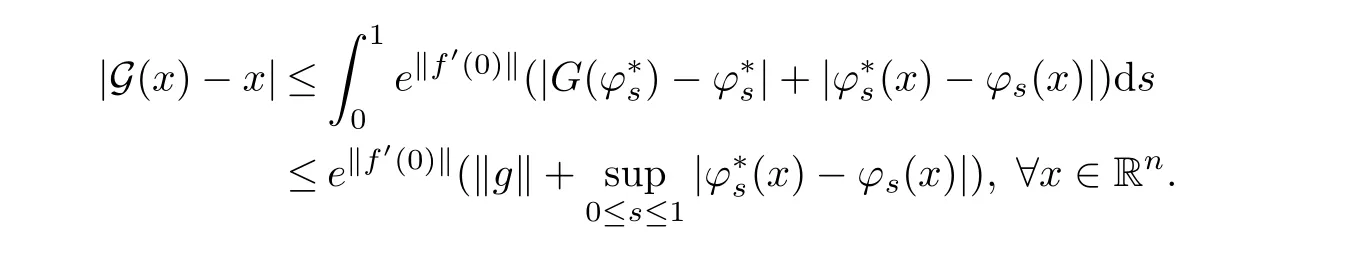
According to the de finition of ??,there exists R>0,such that

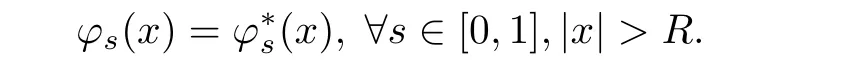
That is to say?M>0 such that

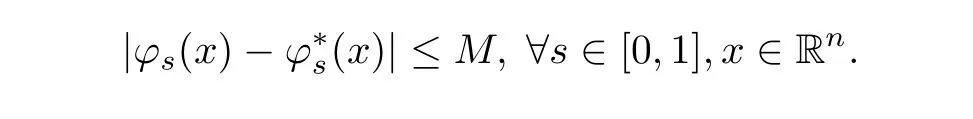
Soas a result,the function G(x)?x is in C(Rn),G=G.

Finally,it remains to show that G is a homeomorphism when restricted to some neighborhood of the origin.Using property(iii)given above,the function h given in property(iii)can be used to de fine a continuous function H by H(x)=x+h(x),so that

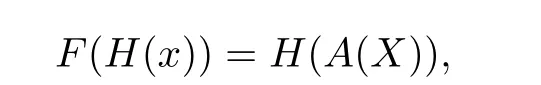
Thus,

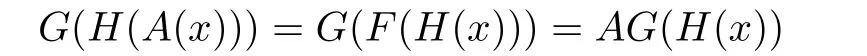
and,with K:=G?H,we have K(A(x))=A(K(x)).Moreover,the function K has the form

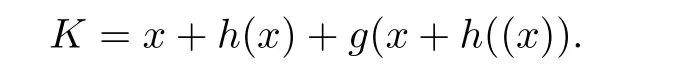
By the construction of G and H,the function

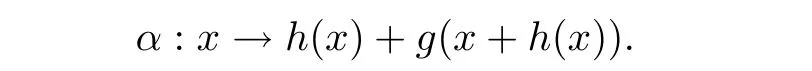
is in C(Rn),and A(α(x))?α(Ax)=0.By Lemma 4.9 of[1],α(x)≡ 0.Therefore,K(x)=x and G(H(x))=x,?x ∈ Rn.Since there is an open set U containing the origin such that the restriction of H to U is a homeomorphism onto its image,we have that G restricted to H(U)is the inverse of H.In particular,G restricted to H(U)is a homeomorphism onto U,and

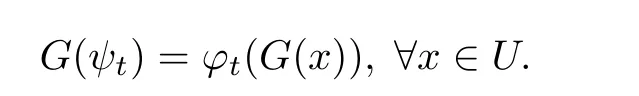
Thus we have proved Theorem 1.1.

[1]CARMEN CHICON.Ordinary Di ff erential Equations with Applications[M].2nd ed New York,NY:Springer 2006.

[2]ZHANG Jin-yan,FENG Bei-ye.Geometric theory and branch problems of ordinary di ff erential equations(in chinese).Peking University press,2000.