李小燕,李美術(shù),高 英

(重慶師范大學(xué)數(shù)學(xué)科學(xué)學(xué)院,重慶 401331)

1 引言

多目標(biāo)優(yōu)化問題中,如何定義最優(yōu)解是首要問題.目前研究的解的概念主要有:有效解,弱有效解和各種真有效解的概念.關(guān)于這些解的存在性,最優(yōu)性條件和對偶等理論是多目標(biāo)優(yōu)化理論研究的主要內(nèi)容.但這些解存在性條件較強(qiáng),通常需要對可行集增加某種意義下的凸性或緊性條件.大量研究表明,在非緊條件下,近似解有可能存在.因此,在非緊條件下研究近似解成為了多目標(biāo)優(yōu)化問題研究的又一重要方向.近幾十年來,一些學(xué)者提出了各種不同的近似解的概念,并進(jìn)行了進(jìn)一步的研究.1979年,Kutateladze[1]首先提出了近似解的概念.1984年,Loridan[2]引進(jìn)了多目標(biāo)優(yōu)化問題 ε-有效解的概念.隨后,一些學(xué)者又提出了幾種近似解的概念(如White[3],Helbig[4]).2006年,Guti′errez等人[5,6]利用co-radiant集定義了多目標(biāo)優(yōu)化問題的一種新的近似解,該近似解推廣并統(tǒng)一了先前給出的諸多近似解的概念(如Kutateladze[1],White[3],Helbig[4]).受文獻(xiàn)[5,6]中研究工作的啟發(fā),高英等人[7,8]在Benson真有效解的基礎(chǔ)上,利用co-radiant集提出了一種近似真有效解的概念.

求解多目標(biāo)優(yōu)化問題一個(gè)重要途徑是將多目標(biāo)優(yōu)化問題轉(zhuǎn)化為數(shù)值優(yōu)化問題,這種轉(zhuǎn)化方法稱為標(biāo)量化方法.標(biāo)量化主要分為線性標(biāo)量化和非線性標(biāo)量化.線性標(biāo)量化主要是在凸性和一些廣義凸性條件下利用凸集分離定理或擇一定理進(jìn)行刻畫.非線性標(biāo)量化主要是通過一些特殊的非線性函數(shù),在非凸分離定理的基礎(chǔ)上進(jìn)行研究.近年來,對有效解,弱有效解和各種真有效解的標(biāo)量化研究可參見文獻(xiàn)[9–15],關(guān)于多目標(biāo)優(yōu)化問題各種近似解的標(biāo)量化研究可參見文獻(xiàn)[16–20].但利用范數(shù)研究多目標(biāo)優(yōu)化問題各種近似解的非線性標(biāo)量化的成果并不多見.因此本文受文獻(xiàn)[7–9,17]的啟發(fā),利用范數(shù)考慮多目標(biāo)優(yōu)化問題近似有效解和近似真有效解的非線性標(biāo)量化刻畫,并舉例說明主要結(jié)果.

2 預(yù)備知識(shí)

令Rn為n維歐氏空間,Rn+為其非負(fù)卦限.設(shè)C?Rn,intC表示C的內(nèi)部,clC表示C的閉包.若C∩(?C)?{0},則稱C 為點(diǎn)集.任取x,y∈Rn,記

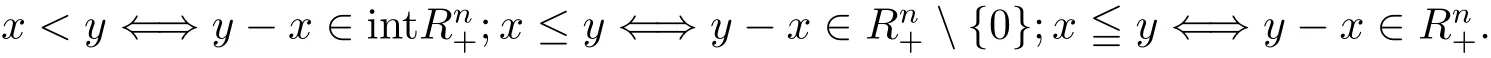
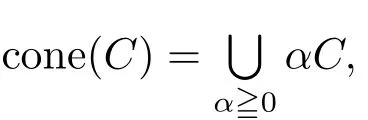
定義2.1[9]設(shè)S?Rn,S的回收錐S+定義為

考慮如下的多目標(biāo)優(yōu)化問題

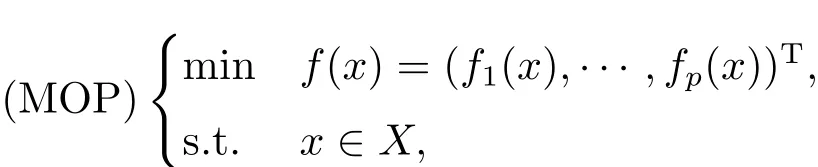
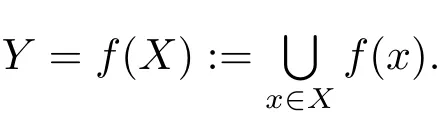
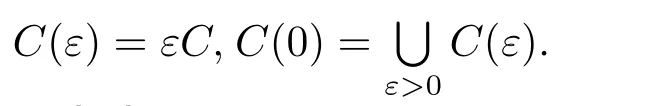
定義2.3[5,7]設(shè)ε∈R,且ε≧0,x∈X,C?Rp為co-radiant點(diǎn)集.

(i)稱為(MOP)問題關(guān)于C的ε-有效解,若

(ii)稱為(MOP)問題關(guān)于C的ε-真有效解,若

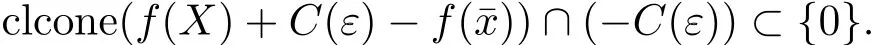
記(MOP)問題關(guān)于C 的ε-有效解和ε-真有效解之集分別為E(f,C,ε)和P(f,C,ε).

Rp中的l∞-范數(shù)和lα-范數(shù)分別定義為

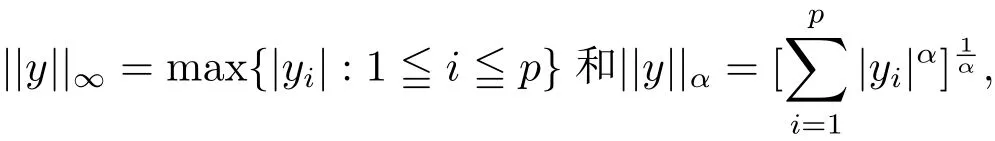
其中

),其中=inf{yi:yi為y∈Y的第i個(gè)分量},i=1,···,p.若滿足則稱為Y的理想點(diǎn).

設(shè)||·||為Rp中的某種范數(shù),為Y=f(X)的理想點(diǎn).考慮如下的非線性標(biāo)量化問題:

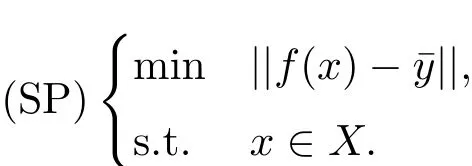
定義2.4設(shè)ε≧0,∈X,α∈[1,∞).

(i)稱為(SP)問題關(guān)于||·||∞的ε-最優(yōu)解,若

(ii)稱為(SP)問題關(guān)于||·||α的ε-最優(yōu)解,若記 (SP)問題關(guān)于 ||·||∞和 ||·||α的 ε-最優(yōu)解之集分別為 A∞(f,ε)和 Aα(f,ε).

3 主要結(jié)果

本節(jié)利用||·||1范數(shù)和||·||∞范數(shù)得到多目標(biāo)優(yōu)化問題近似有效解和近似真有效解的標(biāo)量化結(jié)果.若無特別說明,本節(jié)總假設(shè)C?Rp+為co-radiant點(diǎn)集且0/∈clC.

為了證明的方便,假設(shè)由||·||1范數(shù)的定義,||y1+y2||1≦||y1||1+||y2||1.若y1,y2∈Rp+,則滿足等式關(guān)系這是因?yàn)?/p>

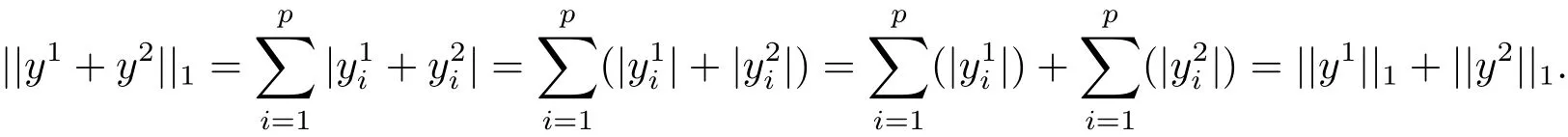
本文在很多地方用到這一結(jié)論.

定理 3.1設(shè) ε≧ 0,0＜ β ＜ d||·||1(0,C),則

(i)A1(f,εβ)? E(f,C,ε);

(ii)若 Y+C(ε)為閉集,則 A1(f,εβ)? P(f,C,ε),

其中 d||·||1(0,C)為 0 到 C 的距離,即 d||·||1(0,C)=inf{||c||1:c ∈ C}.

證設(shè)則由定義2.4有

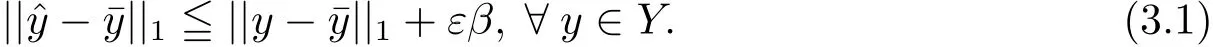
(i)當(dāng) ε＞0時(shí),若∈/E(f,C,ε),則存在使得從而存在c1∈C?R+p,使得.因此由為Y的理想點(diǎn),則即.因此,由||·||1范數(shù)的性質(zhì)可得

這與(3.1)式矛盾.因此∈E(f,C,ε).

當(dāng)ε=0時(shí),若/∈E(f,C,0),則存在從而存在因此

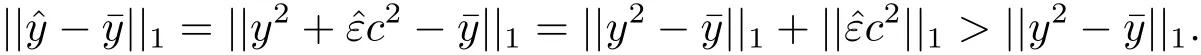
這與(3.1)式矛盾.因此∈E(f,C,0).

綜上,(i)成立.

(ii)當(dāng)ε＞0時(shí),若則存在非零向量

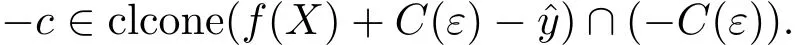
從而存在

若 {βk}有界.不失一般性,假設(shè) βk→ β0,則 β0≧ 0.若 β0=0,由 C ? Rp+有因此則從而這與c∈C(ε)矛盾.若 β0＞0,則由 Y+C(ε)為閉集有

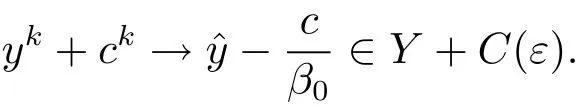
從而存在y0∈Y,d0∈C使得則由||·||1范數(shù)的性質(zhì)可得

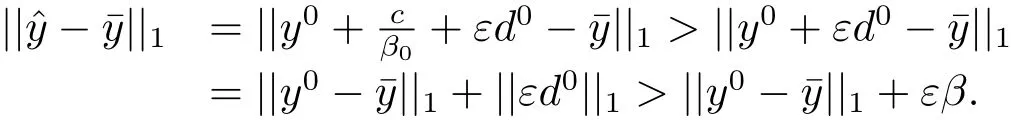
這與(3.1)式矛盾.

若{βk}無界,不失一般性,假設(shè)當(dāng)k→∞時(shí),βk→+∞,則其中,dk∈C?Rp+,?k.即?γ＞0,存在自然數(shù)Kγ,當(dāng)k＞Kγ時(shí),有則

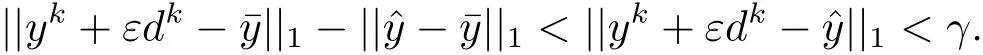
從而.因此存在k?使得事實(shí)上,若對任意的,則存在＞0,使得

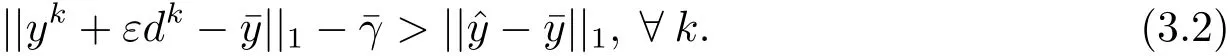
令則對存在自然數(shù)K?,使得當(dāng)k＞K?時(shí)這與(3.2)式矛盾.因此,結(jié)合||·||1范數(shù)的定義可得

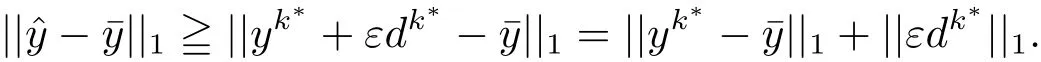
當(dāng)ε=0時(shí),利用ε＞0的證明思路,結(jié)合(i)中ε=0的情況,可得結(jié)論.從而(ii)成立.

注 3.1(i)定理中的 0 ＜ β ＜ d||·||1(0,C)必不可少.若 β =d||·||1(0,C),則 A1(f,εβ)?E(f,C,ε)不一定成立.見例3.1.

(ii)定理中的兩種反包含關(guān)系不一定成立.事實(shí)上,對任意的0＜ β＜ d||·||1(0,C),E(f,C,ε)? clA1(f,εβ),P(f,C,ε)? clA1(f,εβ)都不一定成立.見例 3.1.

(iii)文獻(xiàn)[9]利用||·||α(α∈[1,∞))給出了精確的有效解和真有效解的非線性標(biāo)量化結(jié)果.但對近似解來說,定理中的結(jié)果對其它范數(shù)不一定成立.如||·||∞范數(shù)和||·||2范數(shù).見例3.2.

例3.1令X=R2+,C={(x1,x2)T:x1≥0,x2≥0,x1+x2≥1},f:X→R2,f(x)=x,則Y=f(X)=R2+的理想點(diǎn)之集為R2?且d||·||1(0,C)=1.令ε=1,則

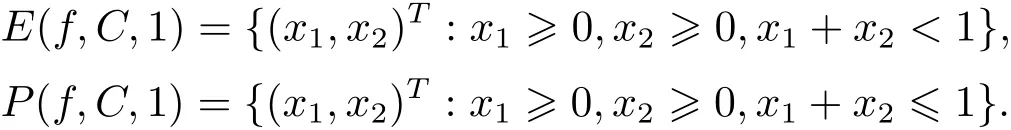
E(f,C,1)的圖象如圖1所示.

若 β =d||·||1(0,C)=1, 則

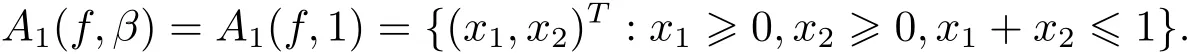
顯然,A1(f,εβ)E(f,C,ε),

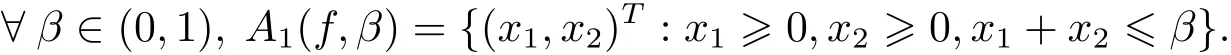
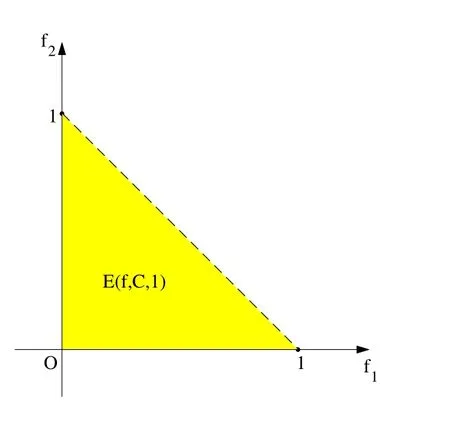
圖1

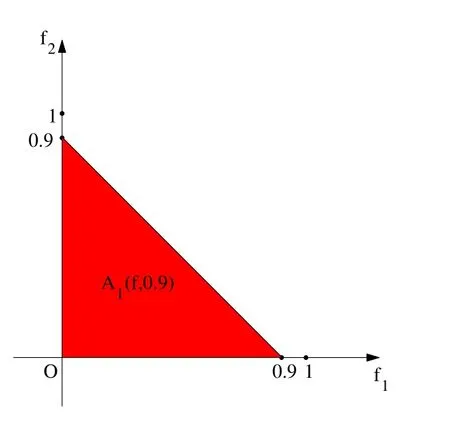
圖2

特別取β=0.9時(shí),A1(f,0.9)的圖象如圖2所示.顯然,clA1(f,β),?0＜β＜1.這說明定理3.1中的兩種反包含關(guān)系不一定成立.

例3.2令

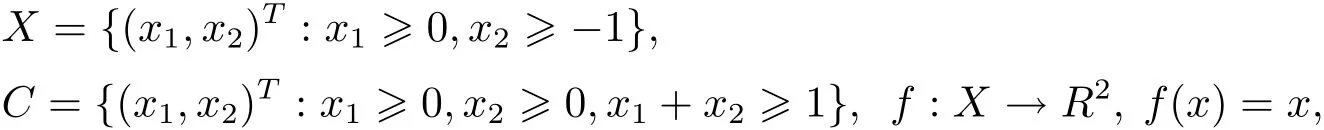
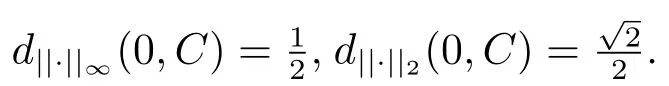
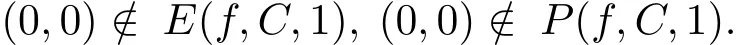
取則

這說明定理3.1的結(jié)果對||·||∞范數(shù)和||·||2范數(shù)不一定成立.

令

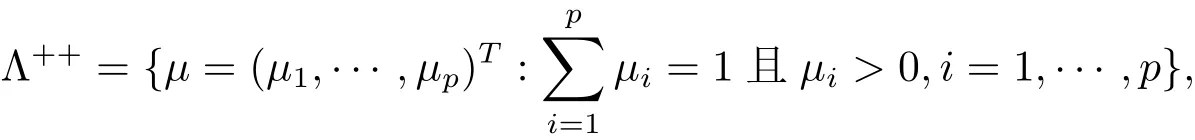
?μ ∈ Λ++,α ∈ [1,∞),y=(y1,···,yp)T∈ Rp+,y 的 (μ,α)范數(shù)定義為的 (μ,∞)范數(shù)定義為其中 μ ⊙ y=(μ1y1,···,μpyp)T.記

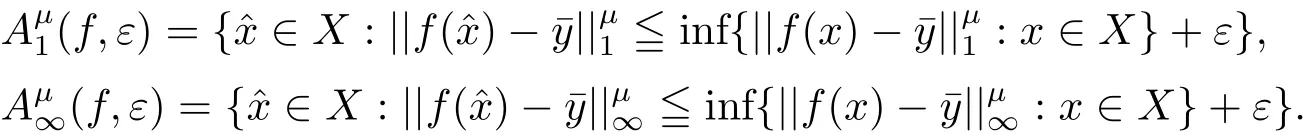
推論3.1在定理3.1的條件下,對任意的μ∈Λ++,有

(i)(f,εβ) ? E(f,C,ε);

(ii)若 Y+C(ε)為閉集,則

證與定理3.1的證明類似.

注3.2當(dāng)ε=0且C(0)∪{0}=Rp+時(shí),推論3.1中的條件和結(jié)果退化到文獻(xiàn)[9]中的定理3.4.8中的特殊情形.

由例3.2知,若定理3.1中的范數(shù)改為||·||∞范數(shù),結(jié)果不一定成立.對||·||∞范數(shù)有如下的標(biāo)量化結(jié)果.

定理3.2設(shè)ε＞0,C?intRp+為co-radiant點(diǎn)集.若

則

(i)A∞(f,∈)? E(f,C,ε);

(ii)若 Y+C(ε)為閉集,則 A∞(f,∈)? P(f,C,ε).

證設(shè)則

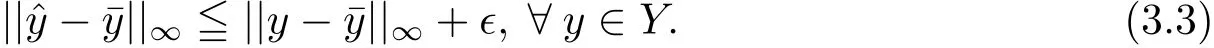
(i)若則存在從而存在c0∈C,使得因此

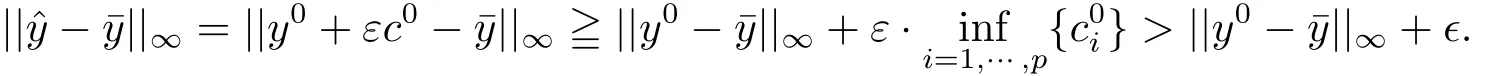
這與(3.3)式矛盾.因此∈E(f,C,ε).

(ii)若則存在非零向量從而存在{βk}?R+{0},{yk}?Y,{ck}?C(ε),使得其中c∈C(ε).

若{βk}有界,假設(shè)βk→β0.由定理3.1(ii)的證明知β00.因此為閉集,有從而存在 y1∈ Y,d1∈ C,使得由c∈C(ε),C?intRp+可得c的每個(gè)分量都大于0.因此

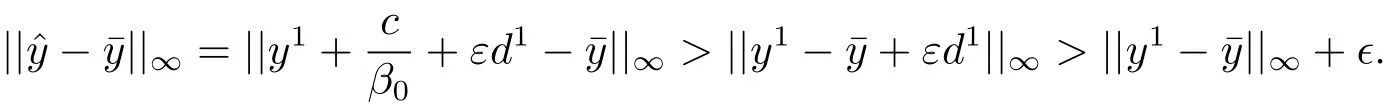
這與(3.3)式矛盾.

若{βk}無界,類似定理3.1(ii)的證明,存在k?使得.因此

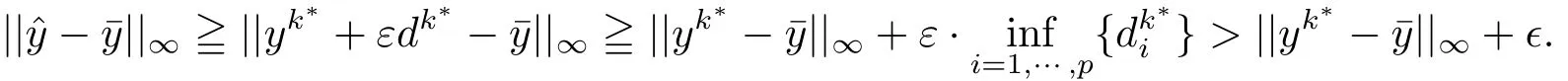
這與(3.3)式矛盾.綜上

注3.3若Y+C(0)為閉集,類似可證A∞(f,0)?P(f,C,0).

定理3.3設(shè)ε≧0.若Y+Rp+為閉集,則

證由Y+Rp+為閉集,易證滿足

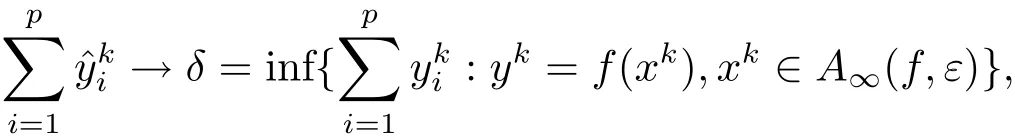
則有界,不妨假設(shè)由Y+Rp+為閉集有∈Y+Rp+,即存在x1∈X,f(x1)=y1∈Y,d1∈Rp+,使得

先證因此

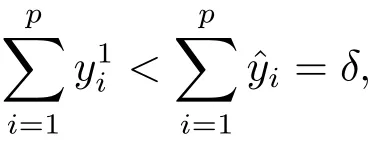
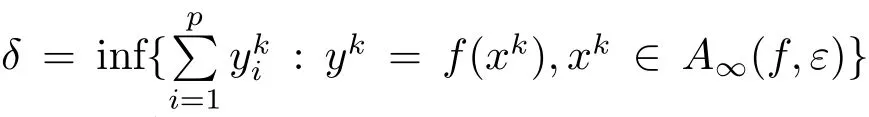
再證.事實(shí)上,若則存在使得由0clC知d20,從而又因?yàn)?/p>

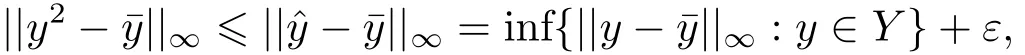
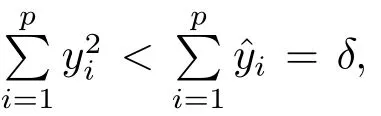
推論3.2在定理3.3的條件下,對任意的

證與定理3.3的證明類似.

注3.4當(dāng)ε=0且C(0)∪{0}=時(shí),推論3.2中的條件和結(jié)果退化到文獻(xiàn)[9]中的定理3.4.9(i).

參考文獻(xiàn)

[1]Kutateladze S S.Convex ε-programming[J].Soviet Math.Doklady,1979,20(2):390–393.

[2]Loridan P.ε-solutions in vector minimization problems[J].J.Optim.The.Appl.,1984,43(2):265–276.

[3]White D J.Epsilon efficiency[J].J.Optim.The.Appl.,1986,49:319–337.

[4]Helbig S.One new concept for ε-efficiency[R].Talk at Optimization Days,1992.

[5]Guti′errez C,Jim′enez B,Novo V.A uni fied approach and optimality conditions for approximate solutions of vector optimization problems[J].SIAM J.Optim.,2006,17(3):688–710.

[6]Guti′errez C,Jim′enez B,Novo V.On approximate efficiency in multiobjective programming[J].Math.Meth.Oper.Res.,2006,64(1):165–185.

[7]Gao Y,Yang X M,Teo K L.Optimality conditions for approximate solutions of vector optimization problems[J].J.Indus.Mgt.Optim.,2011,7(2):483–496.

[8]Gao Y,Hou S H,Yang X M.Existence and optimality conditions for approximate solutions to vector optimization problems[J].J.Optim.The.Appl.,2012,152:97–120.

[9]Sawaragi Y,Nakayama H,Tanino T.Theory of multiobjective optimization[M].Japan:Dpt.Appl.Math.Konan Univ.,1985.

[10]Kaliszewski I.A theorem on nonconvex functions and its application to vector optimization[J].European J.Oper.Res.,1995,80:439–449.

[11]Beldiman M,Panaitescu E,Dogaru L.Approximate quasi efficient solutions in multiobjective optimization[J].Bull Math.Soc.Math.Roumanie Tome,2008,51(2):109–121.

[12]Rastegar N,Khorram E.A combined scalarizing method for multiobjective programming problems[J].European J.Oper.Res.,2014,236:229–237.

[13]李小燕,高英.多目標(biāo)優(yōu)化問題Proximal真有效解的最優(yōu)性條件[J].應(yīng)用數(shù)學(xué)和力學(xué),2015,36(6):668–676.

[14]Zheng X Y.Scalarization of Henig proper efficient points in a normed space[J].J.Optim.The.Appl.,2000,105(1):233–247.

[15]楊豐梅,龔循華.C#-單調(diào)范數(shù)與Henig有效點(diǎn)的切比雪夫標(biāo)量化[J].系統(tǒng)科學(xué)與數(shù)學(xué),2002,22(3):334–342.

[16]岳瑞雪,高英.多目標(biāo)優(yōu)化問題(ε,)-擬近似解的非線性標(biāo)量化[J].數(shù)學(xué)雜志,2016,36(3):615–626.

[17]Guti′errez C,Huerga L,Novo V.Scalarization and saddle points of approximate proper solutions in nearly subconvexlike vector optimization problems[J].J.Math.Anal.Appl.,2012,389:1046–1058.

[18]高英.多面體集下多目標(biāo)優(yōu)化問題近似解的若干性質(zhì)[J].運(yùn)籌學(xué)學(xué)報(bào),2013,17(2):48–52.

[19]Flores-Baz′an F,Hern′andez E.A uni fied vector optimization problem:complete scalarizations and applications[J].Optim.,2011,60(12):1399–1419.

[20]郭輝.向量優(yōu)化問題(C,ε)-弱有效解的一個(gè)非線性標(biāo)量化性質(zhì)[J].運(yùn)籌學(xué)學(xué)報(bào),2015,19(2):105–110.