Synonym Advantage in Evolutionary Signaling Games*
Liping Tang
Institute of Logic and Cognition,Sun Yat-sen University Department of Philosophy,Sun Yat-sen University tanglp3@mail.sysu.edu.cn
Wei Xiong
Institute of Logic and Cognition,Sun Yat-sen University hssxwei@mail.sysu.edu.cn
1 Introductio n
Languages regularly feature synonym,namely,a word means exactly or nearly the same as another word with respect to certain senses.For instance,the words“buy”and“purchase”,“big”and “l(fā)arge”,“quickly”and “speedily”express same things in many contexts.Although those synonymous words are slightly different in meanings,in many contexts they are interchangeable.Consider the sentences“To arrive the goal,we need to work hard”and “To reach the goal,we need to work hard”.The verbs“arrive ”and“reach”are interchangeable in these two sentences.Such a synonymous phenomenon is very common in many languages.
While not catastrophic,the presence of synonym seems,at first blush,suboptimal.It is not only seems unnecessary to have meaning interchangeable words,but it is also energy consuming to learn more words with same functions.So why do we still have synonym in languages?For answering this question,let us first review a comparable phenomenon called ambiguity in languages.
In contrast to synonym,ambiguity represents the feature that words have more than one radically distinct interpretations.As an example,the word “mole”in English can be used to refer to a dark spot on the skin,to a burrowing mammal,to a spy,and to a very large number of objects—usually atoms.This is not even a complete list,as there remain several other less common definitions of the word.The presence of ambiguity seems also suboptimal.We have not run out of possible words,so why not invent a new word for each of the many meanings of“mole”?New words are invented regularly and meanings change over time,yet the existence of ambiguity of this form persist.Why should this be so?Two approaches have been raised to explain this phenomenon,one from the optimality perspective,one from the evolution and learning perspective.Optimality explanations posit a cost to precision.Several authors argue that being precise is expensive as well as unnecessary because,in everyday conversations,context can fill in gaps left by ambiguity(see[11,10,4]).A different,but related,story is told by J?ger([3])and O’Connor([8,7]).They suggest that even without the benefit of context,the cost of having a language with additional expressive capacity may be sufficient to mandate imprecision.From the learning perspective by Tang and Zollman([14]),ambiguous terms have wider applicability and are therefore used more frequently.
The game theoretical model used in those analysis of ambiguity is called Lewis’s signalinggame(see[5]).ThetraditionalLewissignalinggameprovidesabaselinemodel to capture a rather simple communication scenario.In this model there is a finite set of states.For each state,there is an appropriate action for that state.There is a sender,who is aware of the state and can send one of a finite set of signals to a receiver.The receiver is unaware of the state and must choose an action.The receiver can condition her choice ofactionsonthesignalsentbythesender.Boththesenderandthereceiverhavecommon interests,they would like the receiver to take the appropriate action given the state.
Based on this classical game,ambiguity is expressed by the assumption that one signal can be used to talk about several states.In contrast,synonym in signaling games is naturally to be characterized as the case that one state can be expressed by several signals,namely,for any given sate,there are several signals are possibly to be used.We cannot say that the formal characterization of synonym in signaling game captures all perspectives of synonym in natural language,but it at least extract an essential intuitive feature of synonym in natural language.
As a comparable language phenomenon to ambiguity,synonym is plausibly to be explained through the mathematical tool of signaling games as well.Nevertheless,only very few work has been developed along this line.The representative work is done by Alexander et al.([6])on an inventing new signal model.In their work,an invention dynamic of new signals is constructed based on the classical signaling game.The result shows that more new signals than the number of states help agents to avoid imperfect information communication.Therefore,synonym is actually optimal.In this paper,as a complement to their work,we argue that invention is not essential for improving the efficiency of communication.We first develop a similar signaling model without the invention mechanism but with enough number of signals with respect to certain number of states,which in turns achieves the same advantage as the invention model does and sometimes can even do better.Meanwhile,a certain degree of synonym,that is,certain ratioofthenumberofthestatesandsignals,isfoundtobeoptimal,whichresultsfromthe tradeoffbetweentheabundanceadvantageofsignalsandthecostofadditionallearnings.

The remainder of the paper is organized in the following way.Section 2 introduces thebasicmathematicaltoolsusedinthepaperwhichincludestheLewis’ssignalinggame and the learning model called the reinforcement learning dynamic.Section 3 contains a brief summary of the inventing new signal model.In Section 4,we present the synonym signaling model and its advantages with regard to the efficiency of communication.Section 5 provides a comparison analysis of our model and the inventing new signal model.Lastly,we conclude the paper ends with a short conclusion.
2 Lewis’s Signaling Game and Reinforcement Learning
2.1 Lewis’s Signaling Game
Lewis’s signaling game describes a very general communication scenario where a sender observes the situations and sends a signal to a receiver.The receiver takes actions based on the signals he receives.Players have common interests that are decided by receiver’s actions.According to Lewis,the simplest form of a signaling game includes only two states,two signals and two acts.Nature decides the state,the sender chooses a signal to send and the receiver takes an action according to the signal.
The underlining payoff structure of this game takes the following form.When S1occurs and Act1is chosen or S2occurs and Act2is chosen,both players get payoff 1.Otherwise players get 0.According to this payoff structure,the players have common interests.Thus,theplayersarewillingtosharealltheavailableinformationandcooperate as much as possible.
Meanwhile,in contrast to standard games,this signaling game has more than one kind of equilibria with respect to different communication mechanisms.These equilibria includes separating equilibrium,pooling equilibrium and partial pooling equilibrium.They are explained one by one in details in the following.
First of all,the game can have a separating equilibrium under which signals carry complete information about the states.Take the two state,two signal and two act signaling game for illustrations,the following pattern is an example of separating equilibrium.
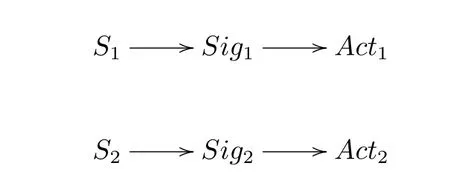
When S1occurs,the sender sends Sig1.By receiving Sig1,the receiver takes Act1.Similarly,when S2occurs,the sender sends Sig2.Under this equilibrium,all the information about the states is communicated successfully between the sender and the receiver.
Meanwhile,the game can have a pooling equilibrium under which signals don not carry information about the states.The sender always sends the same signal for each state and receiver takes the same action all the time.For instance,the following structure shows an example of a pooling equilibrium.
In this example,the sender sends Sig1no matter what nature chooses.For the receiver,he ignores the signals and takes Act1all the time.As a result,no precise information about S1and S2is communicated.
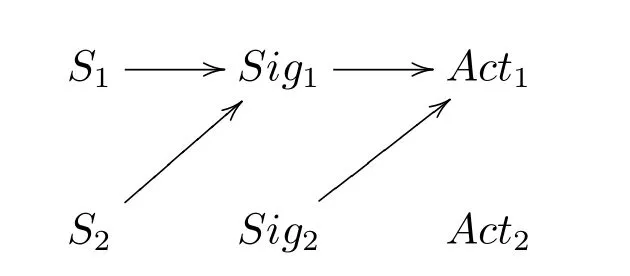
For Lewis’s signaling game with more than two states and two acts,partial pooling equilibrium is possible.For example,the signaling game with three states,three acts and three signals can have the following equilibrium.

In this game,information about the third state is perfectly transferred while the information about S1and S2is not.
For each game,we can calculate players’expected payoffs(utilities)under a certain probability distribution on the set of states.Higher payoff represents a better communication efficiency.We say the games with higher payoffs are more efficient.
Through applying this simple Lewis’s communication model,the properties of the signals and the communicating information can be studied.In classical signaling game,the number of the states usually equals to the number of signals and acts.Nevertheless,this feature can be relaxed according to different purposes.For example,in the study of ambiguity in language,the signaling game usually contains fewer signals than the states such that the feature of ambiguity can be characterized as the case that one signal is used for different states.Similarly,synonym can be expressed in the signaling model as well.More specifically,synonym can be characterized by the signaling structure in which signals are more than the states.Suppose all signals are associated with positive probabilities,it must be the case that for certain states,more than one signals are used to express the same state information,namely,synonym occurs.We shall show below that,synonym posits advantages in an evolutionary signaling game.
2.2 Reinforcement Learning in Signalings

Figure 1:An illustration of reinforcement learning using the two state,two signal,two act Lewis signaling game.
Reinforcement learning is well known in behavioral psychology that describes a strengthen effect that an organism’s future behavior is preceded by a specific antecedent stimulus.The strengthening effect can be measured as a higher frequency of behavior,a longer duration of time and so on.This learning model,due to its generality,has been widely applied in the fields of machine learning,game theory and information theory.Many evolutionary signaling studies([12,7,8])have applied the reinforcement learning rule as their basic learning method because it is not only psychologically natural but also assumes little cognitive abilities from the agents.Considering the structure of the reinforcement learning,it is equivalent to a simple urn model(see[1]).In a classic Polya urn process,we start with an urn containing various colored balls.Then we proceed in the following way.A ball is drawn at random from the urn.Then it is returned to the urn with another ball having the same color.All colors are treated in the same way.As the process continues,some color balls become more superior than others within the urn.
By considering the classical signaling game introduced above,1In this two states,two acts game,players get payoffs when state 1 occurs and act 1 is taken.Similarly,players get benefits when state 2 occurs and act 2 is taken as well.Otherwise,the payoff is 0.the process can be illustrated as follows.The sender has two urns,one for S1and one for S2(see figure 1 for an illustration).Each urn contains balls of two colors.One color represents Sig1,the other represents Sig2.When the sender is informed of the state,she takes the appropriate urn and draws a ball.The color of the ball determines what signal is sent.If the receiver takes the appropriate action,then the sender returns her ball to her urn and adds another one of the same color to the same urn.On the other hand,if the receiver does not take the appropriate action,the sender returns her ball,but does not add another one.
The case for the receiver is similar.He has two urns,one for Sig1and the other for Sig2.Each urn contains balls of two colors,one color represents Act1the other Act2.If the receiver’s act is appropriate for the state,he adds an extra ball to the appropriate urn,otherwise the urn is unchanged.
In Figure 1,round balls indicate signals,triangle ones represent receiver’s actions.Attheinitialstage,instateS1,Sig1andSig2haveequalprobabilitytobechosen(thetop picture in Figure 1).The probability of Sig1in S1can be calculated by 1/(1+1)=0.5.Suppose nature chooses S1and the sender draws the dark ball.As a result,Sig1is sent.Suppose the receiver draws the dark triangle from his Sig1urn.As a result,Act1is chosen by the receiver.Since the receiver took the correct action,one more dark ball and dark triangle should be added to S1urn and Sig1urn respectively.As a result,in the next stage,if S1occurs,the probability of Sig1to be chosen is 2/(1+2)=2/3 and the probability that act Act1is chosen when Sig1is sent increases to 2/(1+2)=2/3.
This learning process can be written in a formal way.Formally,let Sibe all the states,Actjbe all the acts,where i,j=1,2,...,n.wui(t),are the weights for signal u for state i at time t,where u=1,2,...,k.pui(t)is the response probability of signal u for state i at time t.Suppose the initial weights wui(0)=1 for all u and i.Then the updating rule is given as follows.

Similarly,the updating rule and the response rule for the receiver are the following ones.
The updating rule2Actiis denoted as α in the formula.is

Variations of the standard models have been produced to accommodate the need of special purposes.In the next section,we introduce Alexander et al.’s work on inventing new signals.A mutant signal is introduced to the original set of signals such that the model is able to characterize the process of inventing new signals.The result of the invention is that more signals are produced comparing to the size of the state.As a result,synonym phenomenon occurs naturally.

Figure 2:An illustration of inventing new signal learning in the two state,two act Lewis signaling game.
3 Inventing New Signals
The main idea of the inventing new signal model by Alexander et al.is to introduce a mutant signal into the standard reinforcement learning model.Once the mutant signal is triggered,a completely new signal is introduced into the game.For example,if the game starts with a signaling game containing 2 states,2 signals and 2 acts,then after a successful invention of a new signal,the game becomes a game with 2 states,3 signals and 2 acts.Therefore,when there are more signals than the states and each signal is possible to be used,synonym naturally occurs during the inventing new signal model.The process of inventing new signal model can be presented in Figure 2.
The top picture in Figure 2 indicates the initial stage of the game:in state S1,Sig1,Sig2and the mutant signal indicated as the flower symble have equal probability to be chosen.If the mutant ball is not chosen,then the game reduces to the standard reinforcement learning signaling as Figure 1 shows.Once the mutual ball is chosen and the communication is successful,for example,the mutual ball in S1is chosen and A1is taken,then a new signal Sig3(dark square)is added and reinforced in the S1box and A1is reinforced in the new square signal box as the bottom picture of Figure 2 represents.Theprocesscancontinuerepeatedly.Asthesizeofnewsignalsincreases,theprobability of the black ball being picked is decreasing.At some stage,the inventing rate becomes very low.
An example of the bounded number of new signals in the invention model is given in Alexander et al.’s paper.Consider a three state and three act signaling game with states equiprobable.If we start with no signals at all,the number of signals after 100,000 iterations can rang from 5 to 25 as Figure 3 shows3The data and the figure is from Skyrms’book.(see[12],p.130).
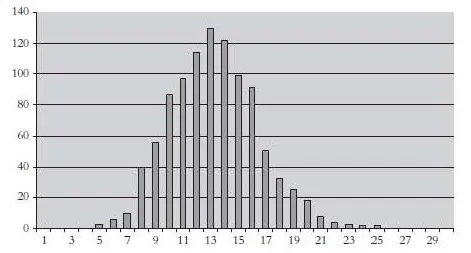
Figure 3:Number of signals after 100,000 iterations of reinforcement with invention in 1,000 trials
As Figure 3 shows,the number of new signals is not so large when comparing to the number of iterations being done.This property matches with our intuition that the probability of drawing the black ball,namely the probability of inventing new signals,decreases as the process continues.
Nevertheless,the number of new signals is relatively large comparing to the number of the states in this three state game.As a result,if all the signals are possibly to be used then synonym must occur.The main contribution of the inventing model is to show that those new signals do make the signaling system more efficient.Alexander et al.present two examples to compare the efficiency of the models with and without inventions.The first example is about a classical reinforcement learning game with three states,three signals and three acts.Around 9%of the trails lead to partial pooling equilibrium4According to the introduction in section 2,partial pooling equilibrium causes no precise information transaction..However,using reinforcement learning with inventions,1000 trails all end up with separating equilibrium.The second example concerns unequal probability of the states.Suppose a game with two states,two signals and two acts.When one state has the probability of 0.9 to occur,44%of trails lead to poolings.On the other hand,if we apply the reinforcement learning with inventions to the unequal probability case,all the 1000 trails exhibit efficient signaling.
As Alexander et al.’s paper shows,the main contribution of the new signals relies on the fact that the abundance of signals can make pooling or partial pooling much less likely.Therefore,the invention mechanism is not essential for the optimality analysis of synonym.In the next section,we investigate a signaling game with a fixed number of signals that are more than the states.We find that a stable ratio of the number of signals and number of states produces the best efficiency for the evolutionary signaling games.
4 Evolutionary Signalings with Synonym
4.1 Synonym and the Efficiency of the Game
The classical Lewis’s signaling game usually assumes that the number of signals is the same as the number of states.In a two state,two signal and two act game,Skyrms([13])has shown that under the replicator dynamic,which is meant to simulate a large,well-mixed population of players that interact in pairs chosen at random,the population always converges to a separating equilibrium.But this result is a convergence result.If a relatively short time of learning5According to O’Connor([9]),the short term behavior of learning also plays important role in the evolution analysis.is considered,we show that more than two signals is more efficient.However,if a game is with n states,n signals and n acts where n>2,then it is shown by Huttegger([2])that a population evolving according to the replicator dynamics has a chance to converge to a partial pooling equilibrium.Thus,imperfect information transmission may occur.Nevertheless,adding more signals with respect to states do present obvious advantages for the game with more than two state.
For verifying the advantage of synonym,in this section,we test the signaling game with a fixed number of signals which is either equal to the number of states,or greater than the number of states.It is found that within a limited time of learning,when the ratio of the number of signals and the number of states is roughly 1.5,the system is most efficient with regard to players’payoffs(utilities).Two groups of simulations are operated to test this result.One is with two states and two acts,whereas the number of signals varies.The other is with three states and three acts while the number of signals varies.The simulation results are collected in the following tables.The average utility in each table is calculated by taking the average of the 200 trails.And for simplicity,all the average utilities have been rounded up to the second decimal point except for the case of games with two states.It is because in games with two states,the utilities are very close between instances.So we round the average utility for the game with two state to the fourth decimal point.

Table 1:Average utility for two states after 2000 iterations with 200 trails
As Table 1 presents,a reinforcement learning signaling is operated for 2000 iterations on a two state,two act game but with the number of signals varies.It shows that the highest efficiency firstly occurs when the number of signals is 3(the ratio of the number ofsignalsand numberof statesis1.5).As thenumber ofsignalsincreases,theefficiency does not increase at the same time.Similar property can be found in the three state and three act game(in Table 2).When the ratio of the number of signals and the number of statesis2,thegamehasthehighestexpectedsuccess.Asthenumberofsignalsincreases,the efficiency of the game does not grow.Similar simulations are ran for the number of states fixed at 4,5,6,7,8.It is found that the change of the average utility all have this up and down patterns.Moreover,the peak values occur at ratios of 1.5,1.6,1.67,1.14,1.25 respectively.It is worth mentioning here that only in the game with two states,the average utilities do not present the liner change as the number of signals increase.We believe it is also because it is very easy for a game with two states to show the separating equilibrium which makes the average utilities extremely close and hard to control.

Table 2:Average utility for three states after 2000 iterations with 200 trails
To conclude,three observations can be emphasized.First,in the two state,two signal and two act game,within a relatively short time of learning,the highest efficiency does not occur when the number of signal is two but when it is three.Second,for the game with n states and n acts(n>2),the peak efficiency occurs when the number of signalsisslightlymorethanthenumberofthestates.Morespecifically,whentheratioof the number of signals and the number of sates is around 1.5,the game reaches the highest efficiency.Thirdly,more signals that excess this ratio do not make much contribution to the efficiency of this game,
For a relatively longer time of learning,the ratio at which the peak of the efficiency occurs may vary but the up and down pattern regarding to the average utility sustains.Additionally,the peak value occurs when the number of signals is slightly bigger than the number of the states,namely,certain degree of synonym is involved.The following table shows the behavior of the three state and three act game with 100000 iterations.

Table 3:Average utility for three states after 100000 iterations with 200 trails
Table 3 shows that with 100000 iterations for a three state game,the peak efficiency first happens when the number of signal is four other than three.
All of the previous examples show the advantages of synonym without invention in the equal-probable state game.As Alexander et al.’s paper states,the second main advantage of the inventing model is to improve the efficiency of the game where the states are not equal probable.To prove the game without invention can achieve the same advantages as the invention model does,we have also tested the unequal probable state games.
Simulations are operated for the games with unequal probabilities on the state set.The results are presented as follows.
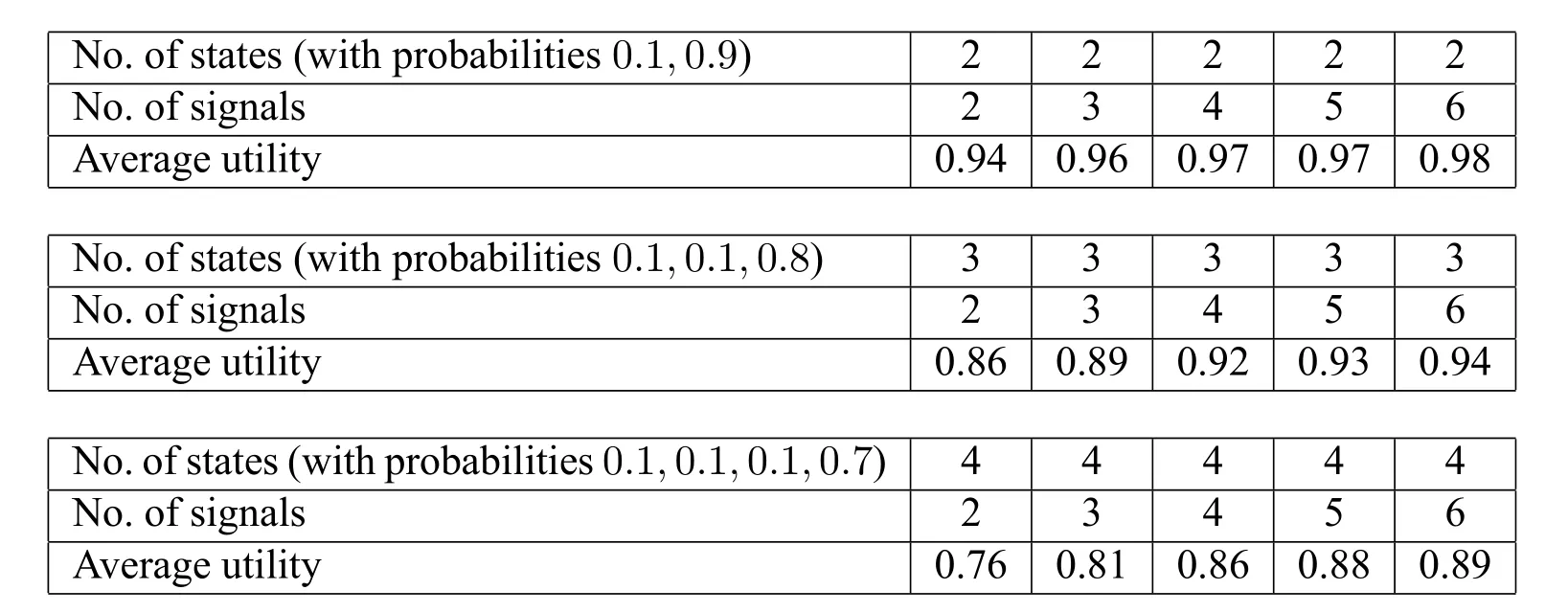
Table 4:Average utility for Unequal Probabilities on States(2000 iterations with 200 trails)
Table 4 shows that in the unequal probability situation for two state,three state and four state games,more signals do improve the efficiency of the game.Therefore,the model without invention but with certain number of signals fixed achieves the same advantages as the invention model does for both equal and unequal probable state games.Inthenextsection,weinvestigatethesimulationsmorecloselyinordertofindthereason triggering the synonym advantage.
4.2 Avoiding Pooling and Partial Pooling
In Lewis’s signaling game,both pooling and partial pooling equilibrium exist.As Section 2 introduces,pooling equilibrium takes the following form for the two state,two signal and two act game.
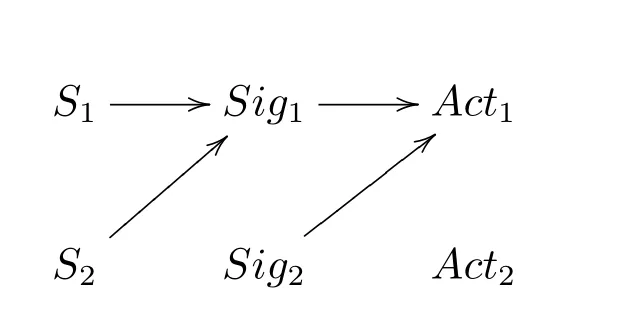
In this equilibrium of sender’s sending Sig1always and receiver’s taking Act1all the time,no information is transmitted.The partial pooling equilibrium occurs in games with more than two state.For example,in a three state,three signal and three act game,the partial pooling equilibrium takes the form as follows.

In this game,some information(about S3)is perfectly communicated while information about S1and S2is not communicated.Poolings and partial poolings are the main reasonsthatcauseinefficientcommunicationinthesignalinggameswherethenumberof the signals is equal to the number of the states.A reasonable conjecture on why synonym advantage exists is that more signals resolve the pooling or partial pooling equilibrium.For verifying the conjecture,we investigate the simulations more closely.
We ran a simulation for the two state and two signal game for 2000 iterations with 200 trails.The result shows that most of the time this game behaves efficiently.The average utilities are 0.99 most of the time.However,among the 200 trails,there are 8 instances where the average utility are less6We care about the instances whose average utilities are apparently worse than the average behaviors of other instances.Without losing generality,3/4 is chosen for convenience.than 3/4 of the average utility 0.958.Take one of them for example,the average utility is 0.54 and the probabilities for each signal and each act are the following.

In the example above,information about the states is not well transformed.In state 1,the sender cannot distinguish between sending signal 1 and sending signal 2,in other words,the probability for him to send Sig1is 0.46 and the probability of sending Sig2is 0.54 when state 1occurs.For the receiver,he is unsure between the two acts given the received signal.As a result,the information is not well transferred and the utility is relatively low.
Forpurposeofcomparison,weoperatethe samesimulationfor atwostate andthree signal game.As a result,the number of expected success rates being less than 3/4 of the average utility becomes 0 which means there is no strict pooling unlike the case with two states and three signals.
When more signals are added,the pooling traps can be avoided.For larger number of states,similar situations are observed.A summary is listed in the following table(Table 5).The number of trails where the expected success rates are less than 3/4 of the average,roughly the number of pooling or partial pooling like cases,are collected for the two state and three state games.It shows that when the number of states equals to the number of signals,the pooling or partial pooling occurs mostly,whereas by adding more signals,pooling or partial pooling decrease significantly.Therefore,we found the reason that why the peak value of efficiency of the system doesn’t occur at the ratio of onebutsomenumberbiggerthanone.Itisbecausewhenthenumberofthestatesandthe number of the signals are equal,there is a higher possibility of the occurrence of poolings or partial poolings.

Table 5:Number of trails whose efficiency is less than 3/4 of the average efficiency(2000 times with 200 trails)
Data from Table 5 confirms our claim that there are more pooling or partial pooling cases happening when the number of the states and number of the signals are the same.When more signals with respect to the states are added,the number of pooling or partial pooling cases decreases.Simulations with longer time of learning exhibit the similar property.The results are presented as follows.
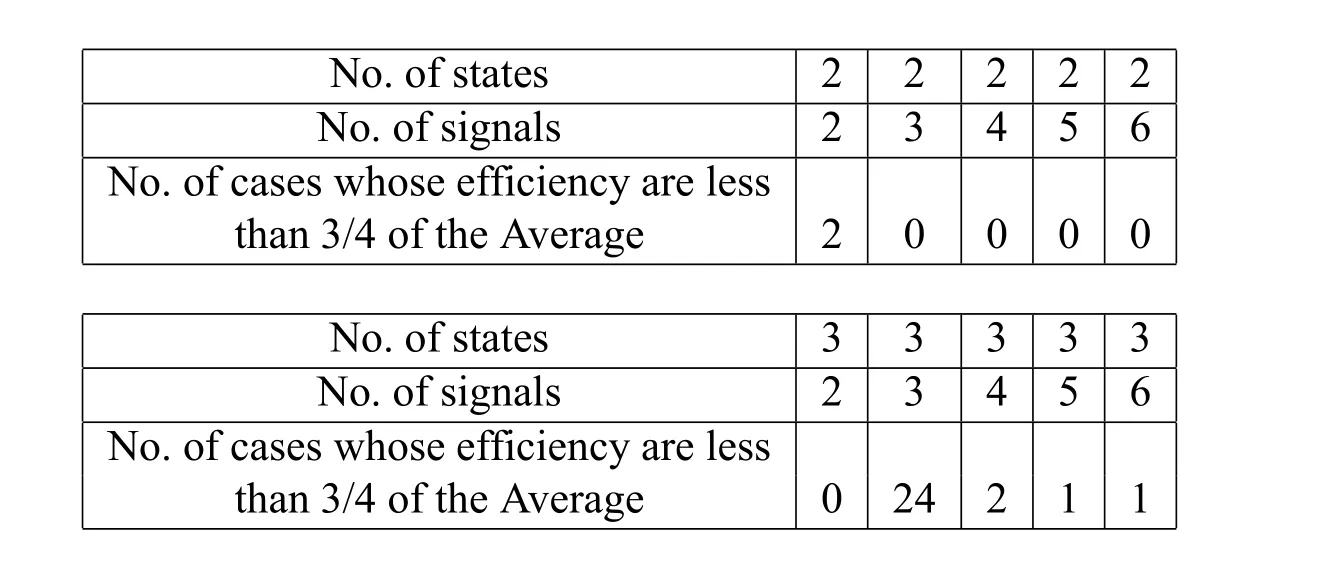
Table 6:Number of trails whose efficiency is less than 3/4 of the average efficiency(10000 times with 200 trails)
To conclude this section,the phenomena of synonym in signaling games,namely,thesignalsaremorethanthestates,doesimprovetheefficiencyofasignalinggamefrom the perspective of evolution and learnings.The underlying reason is that more signals helpthegametoavoidpoolingorpartialpoolingsituations.Aslongasenoughnumberof signalsareprovided,thephenomenaofsynonymistriggeredtoimprovetheefficiencyof thegame.InAlexanderetal.’swork,inventingofnewsignalshasbeenshowntoimprove the efficiency of communications.However,as we have argued,inventing new signals is not essential for such a purpose.A signaling game with more signals provided than the states,namely,when synonym occurs,poolings and partial poolings can be avoided and the communication efficiency is improved.Moreover,we argue in the next section that,in a relatively shorter time of learning,the game without invention but only with certain number of signals behaves even better than the inventing model does.
5 Comparison between Games with and without Invention
The main advantage of inventing new signal model is that it can avoid the pooling and partial pooling traps for both equal and unequal probable state games.We have shownthatthesignalinggameswiththepresenceofsynonymbutnotinvolvinginvention mechanism can achieve the same advantages.In this section,we show that the game without invention behaves even better than the invention model does within a short time of learning.The following tables collect the simulation results with only 50 iterations for both inventing and non-inventing games.
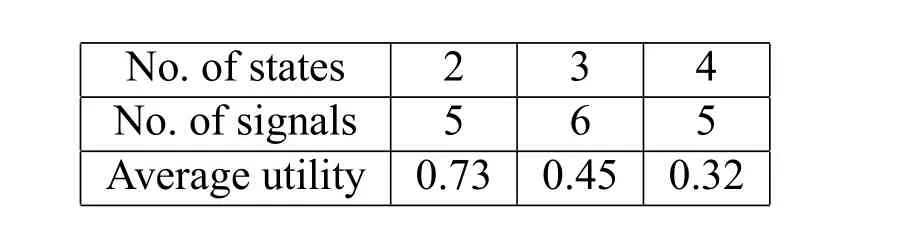
Table 7:Average utility without inventions for a short time of learning(50 times with 20 trails)

Table 8:Average utility with inventions for a short time of learning(50 times with 20 trails)
It is obvious from the above two tables that the game without invention is slightly better than the one with invention.The reason is also obvious.It is because signals being morethanthestatesthantheinventionofnewsignalsplaysanessentialroleonimproving the efficiency.However,in the invention model,if the learning time is too short,there is not enough number of signals invented yet to play the role of synonym.Therefore,the model with enough signals provided initially wins slightly.This result also verifies our intuition that the invention mechanism itself does not contribute to the game whereas the result of the invention that there are more signals than the states plays a more critical role in improve the communication efficiency.
6 Conclusion
The paper tries to provide an explanation for why synonym exists in languages throughagame-theoreticalperspective.First,wehaveshown,inLewis’ssignalinggame,that synonym does seem advantageous in the sense of efficiency.Based on simulation results,the games with signals being slightly more than states do better in terms of communication efficiency than those with equal number of signals and states.Second,it is verified that the reason why synonym dominates is because that synonym helps the signaling games to avoid the pooling and partial pooling situations.Third,the invention mechanism does not play an essential role in improving the efficiency but signals being more than the states do.The signaling game with enough number of signals provided initially is even more efficient than the inventing model sometimes.
Nevertheless,the synonym advantage is only verified here within in the mathematical signaling systems.The gaps between the so-called synonym in machinery system and the real synonym in natural language still exists.The next step of our work is to explore the appropriate connections between the synonym advantage in the mathematical models and natural language.
[1]F.M.Hoppe,1984,“Pólya-likeurnsandtheEwens’samplingformula”,JournalofMathematical Biology,20(1):91–94.
[2]S.M.Huttegger,2007,“Evolution and the explanation of meaning”,Philosophy of Science,74(1):1–27.
[3]G.J?ger,2007,“The evolution of convex categories”,Linguist and Philos,30(5):551–564.
[4]B.Juba,A.T.Kalai,S.Khanna and M.Sudan,2011,“Compression without a common prior:An information-theoretic justification for ambiguity in language”,Proceedings of the Second Symposium on Innovations in Computer Science,pp.79–86.
[5]D.Lewis,1969,Convention:A Philosophical Study,Cambridge:Harvard University Press.
[6]J.McKenzie Alexander,B.Skyrms and S.L.Zabell,2012,“Inventing new signals”,Dynamic Games and Applications,2(1):129–145.
[7]C.O’Connor,2014,“Ambiguity is kinda good sometimes”,Philosophy of Science,82(1):110–121.
[8]C.O’Connor,2014,“The evolution of vagueness”,Erkenntnis,79(4):707–727.
[9]C.O’Connor,2015,“Evolving to generalize:Trading precision for speed”,The British Journal for the Philosophy of Science,68(2):389–410.
[10]S.T.Piantadosi,H.Tily and E.Gibson,2012,“The communicative function of ambiguity in language”,Cognition,122(3):280–291.
[11]C.Santana,2014,“Ambiguity in cooperative signaling”,Philosophy of Science,81(3):398–422.
[12]B.Skyrms,2010,Signals:Evolotion,Learning and Information,New York:Oxford University Press.
[13]B.Skyrms,2014,Evolution of the Social Contract,Cambridge University Press.
[14]L.Tang and K.Zollman,2017,“Ambiguity and Compositional Signaling”,forthcoming.

