華南師范大學(xué)附屬中學(xué)(510630) 郝保國

周期等差(比)函數(shù)再探究

華南師范大學(xué)附屬中學(xué)(510630) 郝保國

近讀文[1],對我啟發(fā)很大.若從不同角度再思考,對周期函數(shù)還會做出更多有意義的推廣.為了便于繼續(xù)探究,先抄錄文[1]相關(guān)的定義：

定義1設(shè)f(x)是定義在某一數(shù)集D上的函數(shù),若存在非零常數(shù)T及函數(shù)h(T),且對?x∈D,有x±T∈D,使得f(x+T)=f(x)+h(T),則稱f(x)為數(shù)集D上的周期等差函數(shù),T稱為f(x)的一個周期,h(T)稱為T所對應(yīng)的f(x)的公差.

若h(T)=b(常數(shù)),稱f(x)為數(shù)集D上的特殊周期等差函數(shù);若h(T)≡0,f(x)就是通常意義上的周期函數(shù).

定義2 設(shè)f(x)是定義在某一數(shù)集D上的函數(shù),若存在非零常數(shù)T及函數(shù)α(T),且對?x∈D,有x±T∈D,使得f(x+T)=α(T)f(x),則稱f(x)為數(shù)集D上的周期等比函數(shù),T稱為f(x)的一個周期,α(T)稱為T所對應(yīng)的f(x)的公比.

若α(T)=a(常數(shù)),稱f(x)為數(shù)集D上的特殊周期等比函數(shù);若α(T)≡1,f(x)就是通常意義上的周期函數(shù).

探究1 若f(x)是以T為周期,h(T)為公差的周期等差函數(shù),則nT(n∈N+)也是f(x)的周期,對應(yīng)公差為nh(T).

證明依條件有f(x+T)=f(x)+h(T),從而

結(jié)論成立.

注若f(x)是以T為周期,α(T)為公比的周期等比函數(shù),則nT(n∈N+)也是f(x)的周期,對應(yīng)公比為[α(T)]n.

探究2 若f(x)是以T為周期,α(T)為公比的周期等比函數(shù),且f′(x)存在,則f′(x)仍為周期等比函數(shù).

證明

所以,f′(x)仍是以T為周期,α(T)為公比的周期等比函數(shù).

注若f(x)是以T為周期,h(T)為公差的周期等差函數(shù),且f′(x)存在,則f′(x)為周期等差函數(shù).

探究3 若f(x)的圖像有兩個對稱點M(a,b),N(c,d),則f(x)為特殊周期等差數(shù)列,周期T=2(a-c),公差D=2(b-d).

證明因f(x)的圖像關(guān)于點M(a,b)對稱,則知f(x)的圖像上任一點P(x,y)關(guān)于M(a,b)的對稱點Q(2a-x,2b-y)也在f(x)的圖像上,有

在③中以2c-x代x,有f[2(a-c)+x]=f(x)+2(b-d).結(jié)論成立.

探究4若f(x)=x+g(x),則f(x)為周期等差函數(shù)的充要條件是g(x)為周期等差數(shù)列.

證明充分性.若g(x)為周期等差函數(shù),不妨設(shè)g(x+T)=g(x)+h(T),則

所以,f(x)為周期等差數(shù)列,周期為T,對應(yīng)公差是T+h(T).必要性.g(x)=f(x)-x,若f(x)為周期等差函數(shù),不妨設(shè)f(x+T′)=f(x)+h′(T′),則

所以,g(x)為周期等差函數(shù),周期為T′,對應(yīng)公差是h′(T′)-T′.

探究5f(x)(x∈R)是周期等比函數(shù)的充要條件是存在周期函數(shù)φ(x)及a＞0,使得f(x)=axφ(x).

證明充分性.若存在周期函數(shù)φ(x)及a＞0,使得f(x)=axφ(x).不妨設(shè)φ(x)的周期為T,則f(x+T)=ax+Tφ(x+T)=aT[axφ(x)]=aTf(x).所以,f(x)是周期等比函數(shù),周期為T,對應(yīng)公比為aT.

探究6 若f(x)是周期為T,公差為kT(k∈N+)的周期等差函數(shù),則f(x)的n次迭代函數(shù)f(n)(x)為周期等差函數(shù).

證明依條件有,f(x+T)=f(x)+kT,

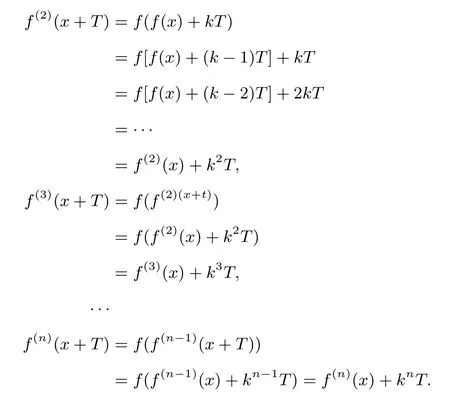
所以,f(n)(x)是周期為T,對應(yīng)公差為knT的周期等差函數(shù).

探究7 設(shè)f(x)是R上的不減函數(shù),并且是周期與公差均為T的特殊周期等差函數(shù),求證：對任意正整數(shù)m和n,有

證明依條件有f(x+T)=f(x)+T,由探究6知f(n)(x+T)=f(n)(x)+T,得f(n)(T)=f(n)(0)+T.任取0≤x≤T,由f(x)是R上的不減函數(shù),易知f(n)(x)也是R上的不減函數(shù),則有

證明依條件有f(x+T)=f(x)+mT,令f(x)=mφ(x),則φ(x+T)=φ(x)+T,構(gòu)造函數(shù)φ′(x)=φ(x)-x,因φ′(x+T)=φ(x+T)-(x+T)=φ(x)+T-(x+T)=φ(x)-x=φ′(x),則知φ′(x)=φ(x)-x是周期為T的函數(shù).

設(shè)0≤x≤T,由f(x)是R上的增函數(shù),知φ(x)亦是R上的增函數(shù),所以φ(0)≤φ(x)≤φ(T)=φ(0)+T,因x-T≤0≤x,所以φ(0)+x-T≤φ(x)≤φ(0)+x+T,

由φ′(x)=φ(x)-x的周期性知,①式對R上的任一x成立.兩端乘以m得,

同樣,②式對R上的任一x成立.由②式有

[1]郝樂,馬乾凱,郝一凡.周期等差函數(shù)與周期等比函數(shù)[J].沈陽大學(xué)學(xué)報：自然科學(xué)版,2013.25(3)：253-254