XU Jin

?

Theory on Structure and Coloring of Maximal Planar Graphs(2) Domino Configurations and Extending-Contracting Operations

XU Jin*

(,,100871,) (,,100871,)

The first paper of this series of articles revealed that Four-Color Conjecture is hopefully proved mathematically by investigating a special class of graphs, called the 4-chromatic-funnel, pseudo uniquely-4- colorable maximal planar graphs. To characterize the properties of such class of graphs, a novel technique, “extending-contracting operation”, is proposed which can be used to construct maximal planar graphs. The essence of this technique is to study a special kind of configurations, domino configurations. In this paper, a necessary and sufficient condition for a planar graph to be a domino configuration is constructively given, on the basis of which it is proposed to construct the ancestor-graphs and descendent-graphs of a graph. Particularly, it is proved that every maximal planar graph with orderand minimum degreehas an ancestor-graph of orderor. Moreover, an approach is put forward to construct maximal planar graphs recursively, by which all maximal planar graphs with order 6~12 and minimum degreeare constructed. The extending-contracting operation constitutes the foundation in this series of articles.

Maximal planar graphs; Extending-contracting operations; Domino configurations; Ancestor-graphs; Descendent-graphs; Recursive construction approach

1 Introduction

In mathematics, there are three remarkable conjectures: FERMAT's Conjecture (FERMAT's Last Theorem), GOLDBACH's Conjecture, and Four-Color Conjecture. The primary reason why these conjectures are widely known is the easy understanding of them. Specifically, FERMAT’s Conjecture claims that no three positive integersandthat satisfy the equationx+y=zfor any integer, GOLDBACH Conjecture says that every even integer greater than 2 can be written as the sum of two primes, and Four-Color Conjecture states that every map in the world can be colored with four colors such that no two adjacent regions, sharing a common boundary, receive the same color. Clearly, these conjectures are readily comprehensible for people, even for those who receive an education at only junior high school level. In particular, Four-Color Conjecture is much more understandable, which is possible to be understood by uneducated persons. To compare with the description of Four-Color Conjecture, the approach to confirm it is considerably difficult. In 1976, APPLE and HAKEN declared that they had got a computer-assisted proof of Four-Color Conjecture, but this result is still not satisfying in mathematics. Therefore, finding a mathematical method to concisely solve the Four-Color Conjecture is still open. Given that the studying object of Four-Color Conjecture can be confined to maximal planar graphs, we are necessary to investigate the structural properties and construction methods of such class of graphs.

In fact, as early as 1891, EBERHARD[4]had begun a deep research on the construction problem of maximal planar graphs, and devised an operational system to generate maximal planar graphs.We useto denote this system, where,, andare called original object, operation set, and generating operations, respectively (see Fig. 1).

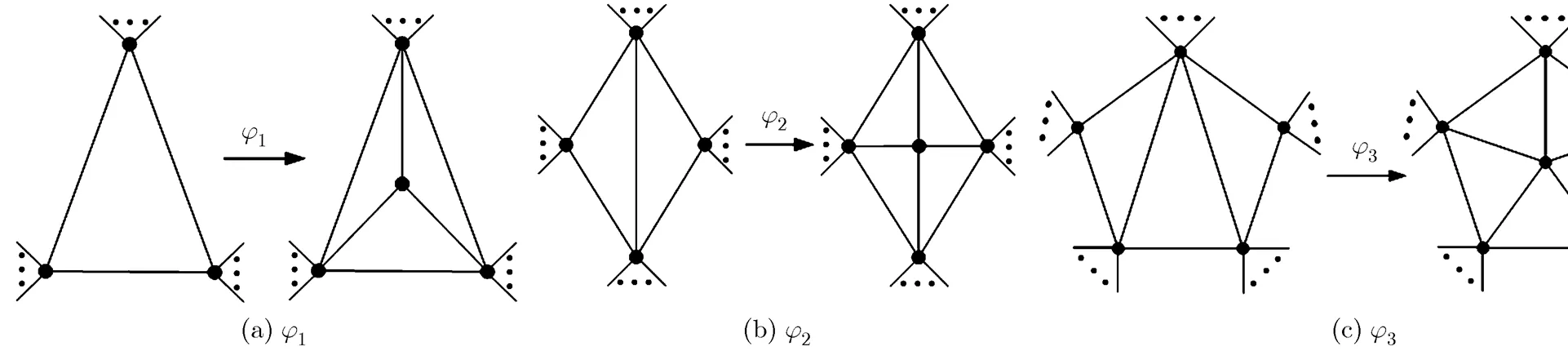
Fig. 1 Three generating operations used by EBERHARD to construct maximal planar graphs

From 1999 to 2000, WANG[5,6]independently proposed a similar method as that of EBERHARD to construct maximal planar graphs. On the basis of EBERHARD’s method, he extend the length of purely-chord cycles from 3, 4, 5 to arbitrary.

After EBERHARD’s work, the research on this topic advanced little for almost a century, and drew our attention again in 1974 with the study of constructing all 5-connected maximal planar graphs by BARNETTE[7]and BUTLER[8], independently. Different from EBERHARD’s operational system, BARNETTE and BUTLER’s operational system is, in which the original objectis the icosahedron and the operation set is(see Fig. 2; the ellipses attached to the vertices in the description of the generating operations denote any number (zero or more) of edges satisfying). In short, BARNETTE and BUTLER’s method starts with the icosahedron and uses the operations,, andto generate 5-connected maximal planar graphs.

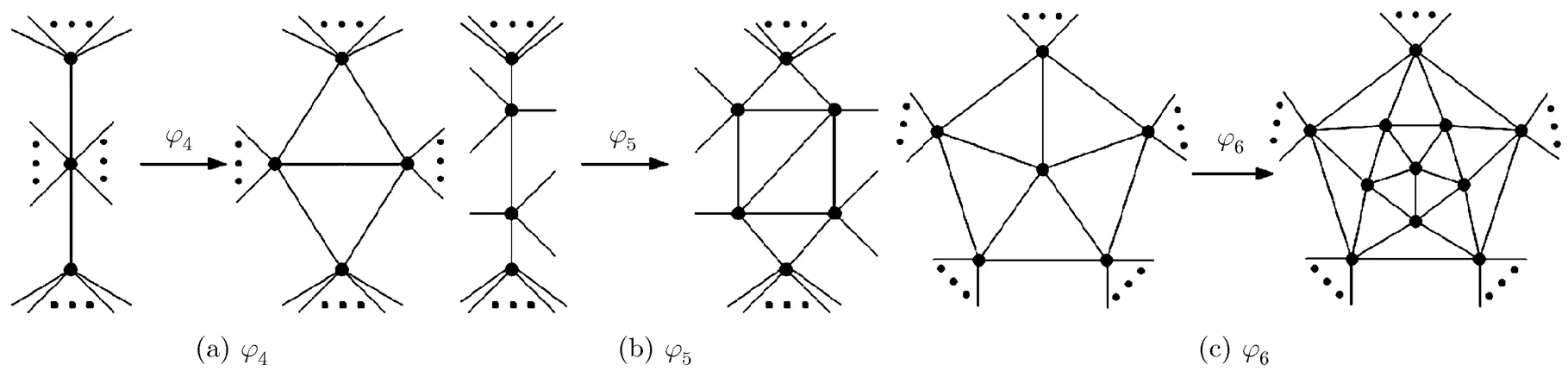
Fig. 2 BARNETTE and BUTLER’s operations

In 1983, BATAGELJ[9]improved the method of BARNETTE and BUTLER by changing one of the operations. Specifically, he used a new generating operationinstead ofand kept the remaining parts unchanged. The new operational system is denoted by, whereis called the flip operation (Fig.3).

The research of flip operation has been a long history. This concept was introduced by WAGNER[10]in 1936. Up to now, the flip operation has been studied very thoroughly, so we will give a specific discussion about it in the following paragraph.

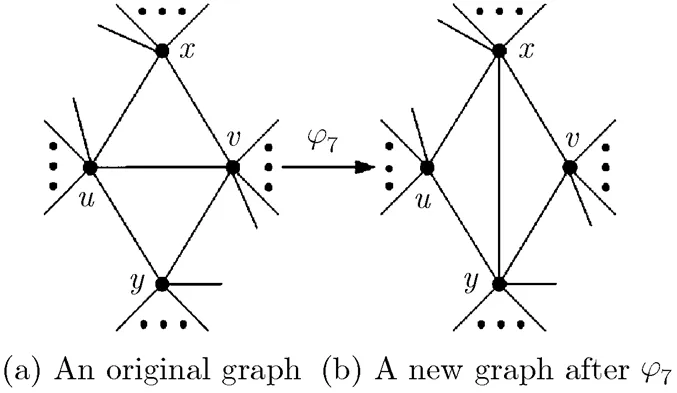
Fig. 3 The edge flip operation

In 2005, further works were done by BRINKMANN and MCKAY[11]in terms of BARNETTE, BUTLERY, and BATAGELJ’s conclusions. They gave an efficient method to construct all simple maximal planar graphs of minimum degree 5. Moreover, they pointed out the restrictions using, andto construct the maximal planar graphs with minimum degree 5, which contain separating 3-cycles, 4-cycles, and 5-cycles respectively, and gave an algorithm to construct the graphs on computers. Particularly, by constructive method, they listed the number of maximal planar graphs of minimum degree 5 with orders from 12 to 40, where the numbers of 3-connected, 4-connected, and 5-connected 40-vertex maximal planar graphs of minimum degree 5 are 8469193859271, 7488436558647, and 5925181102878, respectively. Note that they used the canonical construction path method proposed by MCKAY[12]in 1998, to avoid the generation of isomorphic copies in his computer program.

The study on algorithms for generating maximal planar graphs also inspires many scholars’ interests. In 1996, AVIS[13]gave an- time algorithm for generating all-rooted 3-connected maximal planar graphs onvertices by the reverse search technique. First, construct an-vertex canonical maximal planar graph (contains exactly two vertices of degree); then generate all-rooted 3-connected maximal planar graphs of orderby means of flip operations.

In 2004, NAKANO[14]gave a simple algorithm to generate all 3-connected-rooted plane triangulations with at mostvertices. He showed that all 3-connected rooted plane triangulations with exactlyvertices and exactlyvertices on the outer face can be generated intime without duplications. In 2007, BRINKMANN and MCKAY[15]introduced the Plantri-operational rule based on the canonical configuration path[12], and gave the program plantri[16].

It is clear that edge flip operation transforms a maximal planar graph into another one with the same number of edges. Naturally, this raises a question: can an arbitrary-vertex maximal planar graph be transformed into a given-vertex maximal planar graph through a finite sequence of flips? In 1936, WAGNER[10]first addressed this question with the positive answer. Although the number of-vertex maximal planar graphs is exponential in, WAGNER avoided the issue of graph isomorphism by converting a maximal planar graph into a canonical maximal planar graph, and proved that any given maximal planar graph can be transformed into a given-vertex maximal planar graph by at mostedge flips.

After that there are lots of scholars working on this topic, and improving the upper bound. In 1993, NEGAMI and NAKAMOTO[17]proved that any given-vertex maximal planar graph could be converted into the canonical maximal planar graph viaedge flips. KOMURO[18]proved that any two-vertex maximal planar graphs can be transformed into mutually through at most(or) edges flips for(or). MORI[19]. showed that any Hamiltonian maximal planar graph onvertices could be transformed into a canonical maximal planar graph by at mostedge flips, preserving the existence of HAMILTON cycle. He also proved that any-vertex maximal planar graph could be made 4-connceted by at mostedge flips, and any two maximal planar graphs onvertices could be converted into each other by at mostedge flips.

In 2001, GAO.[20]proved that every maximal planar graph onvertices contains at leastflippable edges and that there exist some maximal planar graphs that contain at mostflappable edges. Moreover, he showed that there were at leastflippable edges in a maximal planar graphif, and the bound was tight in certain cases.

In 2001, BOSE.[21]showed that a maximal planar graph onvertices could become 4-cconnected by at mostedge flips, and any two maximal planar graphs onvertices could be transformed into each other by at mostedge flips.

The above review the construction methods and algorithms. By the existing methods of generating maximal planar graphs, it is very hard to associate the structure with coloring. In this paper, we introduce a novel technique, extending- contracting operation, to construct maximal planar graphs. Our method can well associate the structure of a maximal planar graph with its coloring. We prove that any two maximal planar graphs can be transformed into each other by four pairs of basic extending-contracting operators. The essence of this technique is to study a special kind of configurations, domino configurations. To characterize the properties of such class of configurations, we propose an operational system to generate all of the domino configurations, on the basis of which a method is proposed to construct all of the ancestor-graphs and descendent-graphs of a graph. Particularly, we show that every maximal planar graph with orderand minimum degreehas an ancestor-graph of orderor. Moreover, we give an approach to construct separable maximal planar graphs.

Notice that, to prove Four-Color Conjecture according to the idea proposed in the first paper of this series of articles[22], we need to use the extending-contracting operational system introduced in this article.

From coloring perspective, adding or deleting vertices of degree 3 in a 4-colorable maximal planar graph has no effect on the study of relation between structure and coloring. Therefore, unless otherwise stated, graphs considered in this paper are assumed to be a maximal planar graph with minimum degree. As an example for illustrating the extending-contracting operational system, all maximal planar graphs with order 6~12 and minimum degreeare constructed in this paper.

All graphs considered in this paper are finite, simple and undirected. For a given graph, we use,,, andto denote the vertex set, the edge set, the degree of, and the neighborhood ofin(the set of neighbors of), respectively, which can be written as,,, andfor short. The order ofis the number of its vertices. A graphis a subgraph ofifand. For a subgraphof, iffor any, thenis called an induced subgraph ofor a subgraph ofinduced by, denoted by. Two graphsandare disjoint if they have no vertex in common. By starting with a disjoint union ofand, and adding edges joining every vertex ofto every vertex of, one obtains the join ofand, denoted by. We writeandfor the complete graph and cycle of order, respectively. The joinof a cycle and a single vertex is referred to as a wheel, denoted by(the examplesare shown in Fig. 4), whereis called the wheel-cycle ofand the vertex ofis called the wheel-center of. If, we also denote bythe wheel-cycle of.

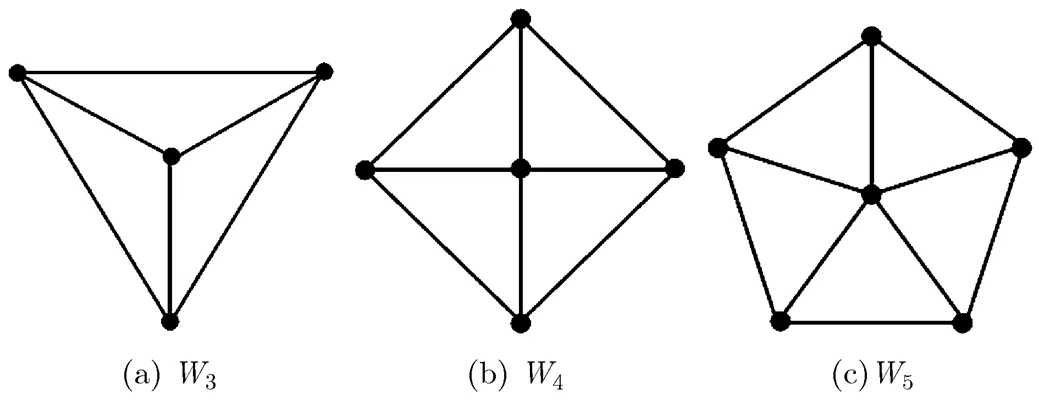
Fig. 4 Three wheels , and

A graph is said to be planar if it can be drawn in the plane so that its edges intersect only at their ends. Such a drawing is called a planar embedding of the graph. Any planar graph considered in the paper is assumed one of its planar embedding. A maximal planar graph is a planar graph to which no new edges can be added without violating planarity. A triangulation is a planar graph in which every face is bounded by three edges (including its infinite face). It can be easily proved that maximal planar graphs are triangulations, and vice versa. A graph is separable if one of its proper induced subgraph is a maximal planar graph, otherwise, it is non-separable.

The definitions and notations not mentioned here can be found in Refs. [22,23].

2 Basic Extending-contracting Operational System

In this section, we introduce the basic extending-contracting operational system. This system consists of two parts: operating objects and basic operators, where the operating objects are maximal planar graphs; the basic operators include four pairs of operators: the extending-wheel operation and the contracting-wheel operations,The function of this system is: starting with, we can generate any given maximal planar graph by using the four pairs of operators repeatedly.

The extending 2-wheel operation consists of 2 steps: (1)add a new edge between two adjacent vertices, which will generate a 2-parallel edge (namely a 2-cycle, a cycle of order 2); (2)add a new vertex in the face of the 2-cycle and connecting the new vertex to the two vertices of the 2-cycle. Naturally, the object of extending 2-wheel operation is an edge of a maximal planar graph, see Fig. 6(a).

For a graph with 2-wheels, the contracting 2-wheel operation is to delete the wheel-center of a 2-wheel and the two edges incident with the wheel-center, and then delete one of the parallel edges of the 2-cycle. The procedures of extending and contracting 2-wheel operations are shown in Fig. 5.

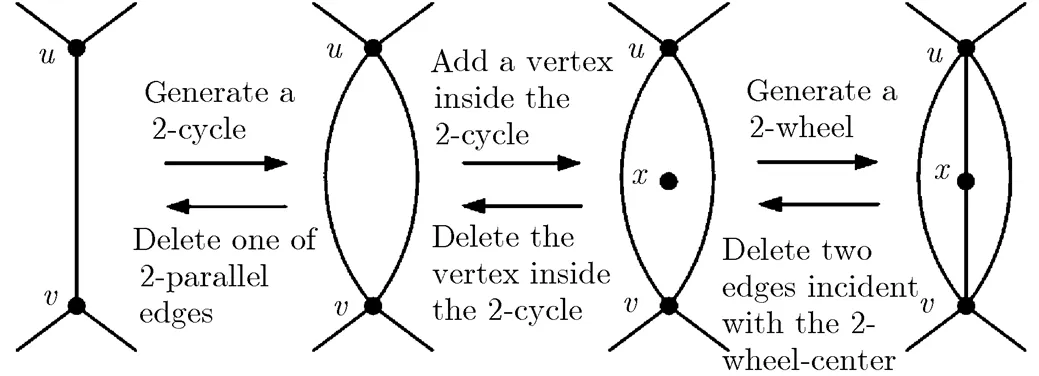
Fig. 5 The procedures of extending

and contracting 2-wheel operations

The extending 3-wheel operation is to add a new vertex in a certain face of the maximal planar graph, and connect it to the three vertices of the face, respectively. The object of extending 3-wheel operation is a triangle of a maximal planar graph, see Fig. 6(b). The contracting 3-wheel operation is to delete a certain 3-degree vertex and its incident edges.

The contracting 4-wheel operation includes three steps: (1)to delete a certain 4-degree vertex and the edges incident with it; (2)to identify a pair of the non-adjacent vertices; (3)to delete one of 2-parallel edges if there exists 2-parallel edges in

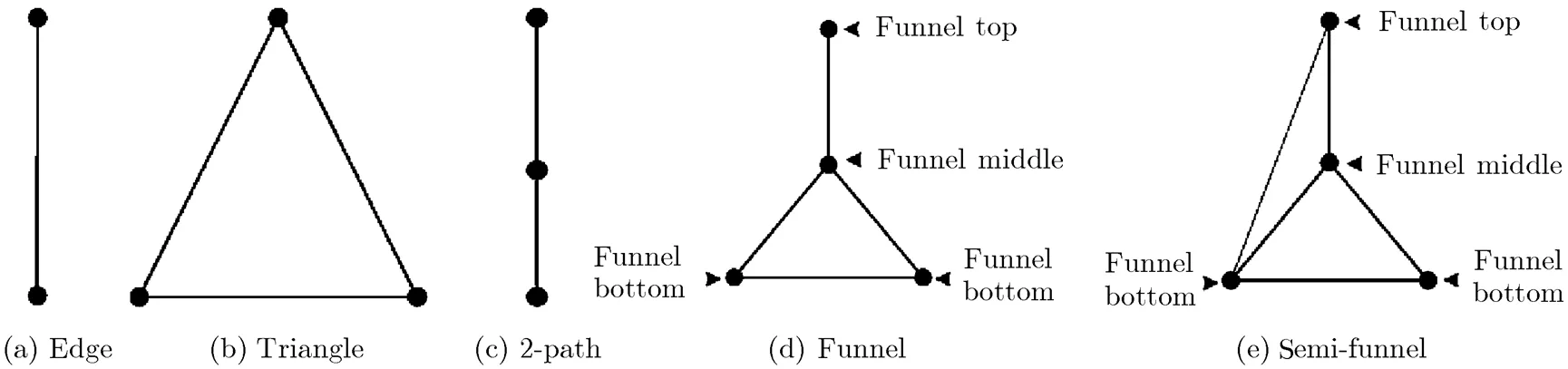
Fig. 6 The objects of basic extending wheel operations and semi-funnel

Fig. 7 The procedures of extending and contracting 4-wheel operations

the obtained new graph, and no vertex in the face of 2-parallel edges. This procedure is shown in Fig. 7 (see the fifth to the first graph).

The graph shown in Fig. 6(d) is called a funnel, denoted by, where the 1-degree vertex is the top of the funnel, the 3-degree vertex is the middle of the funnel, and the two 2-degree vertices are the bottoms of the funnel. As the middle and two bottoms ofare vertices of a triangle, we also writeby, whereis the top of. If we add an edge between the top and one of bottoms of the funnel, then we call the new graph a semi-funnel (see Fig. 6(e)). Letbe an induced subgraph of. We calla funnel (or semi- funnel) subgraph ifis isomorphic to a funnel (or a semi-funnel). The semi-funnel subgraph is one of objects to construct ancestor-graphs or descendent-graphs of a graph.

Fig. 8 The procedures of extending and contracting 5-wheel operations

Obviously, for a non-separable maximal planar graphwith, we can see that bothandare maximal planar graph, while they are possible to be separable, or have minimum degree 2 or 3. No matter what the degrees of them are, the following result holds.

Theorem 1 can be easily obtained, and we leave the proof to the reader.

3 Domino Extending-contracting Operational System

3.1 Consecutive extending-contracting operation and domino extending-contracting operation

The previous section introduces four pairs of basic extending and contracting operators, which can generate maximal planar graphs. More importantly, the method proposed can associate structure with coloring easily. Starting with3, we can generate any given maximal planar graph using this system. Generally, to generate a desired graph we need to implement many times of extending and contracting operations. We refer to such a sequence of extending and contracting operations as a consecutive extending-contracting operation.

Recall that the maximal planar graphs considered in this paper are assumed to be those with minimum degree at least 4. Therefore, if the minimum degree oforis 2 or 3, then we need to further implement extending or contracting operations repeatedly until we obtain a graph withor.

implement a contracting 2-wheel or 3-wheel operation, and denote the resulting graph by. If, we refer to these two successive contracting wheel operations as a domino contractingwheel operation. Ifor 3, then we implement contracting 2-wheel or 3-wheel operations repeatedly until aor a graphwithis obtained. If, we refer to thesecontracting wheel

operations as a domino contracting wheel operation; if, we calla dominoable maximal planar graph. Fig. 9(a) shows a dominoable maximal planar graphof order 9, and Fig. 9(b) isthat is obtained from Fig. 9(a) by implementing one contracting 4-wheel operation on the 4-wheel (marked by bold lines in Fig. 9(a)), in the process of whichare identified. As there exists two 2-degree vertices in, we implement contracting 2-wheel operations on the two 2-degree vertices respectively. The resulting graphis shown in Fig. 9(c), which has minimum degree 3. Therefore, we continually conduct contracting wheel operations till the resulting graph isor the one with minimum degree. The process of a domino contracting wheel operation onis illustrated in Fig. 9(a)~9(d).

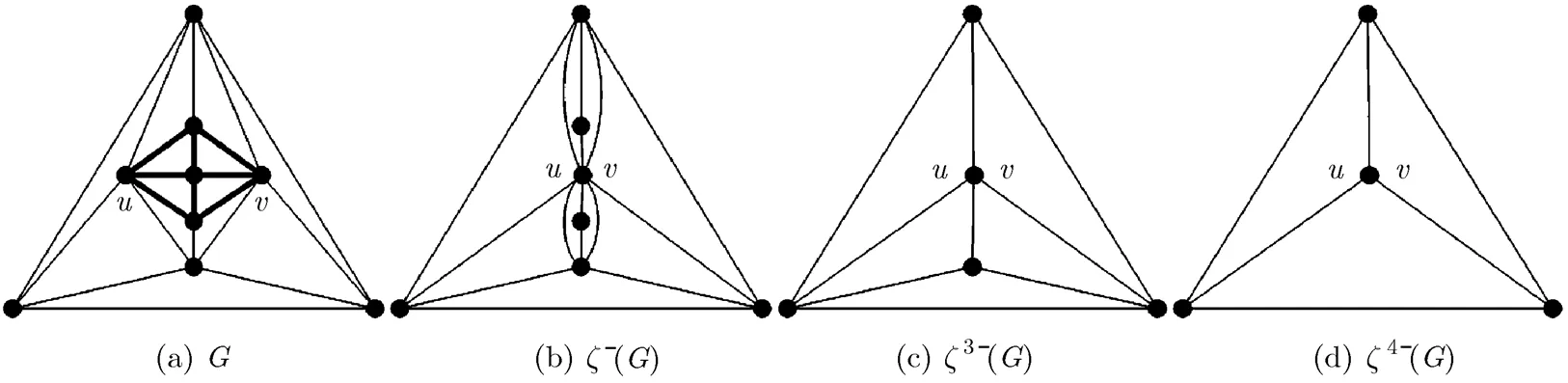
Fig. 9 A dominoable maximal planar graph of order 9

conducting an extending 4-wheel (or 5-wheel) operation on(or), then we call the extending 4-wheel (or 5-wheel) operation a domino extending wheel operation. Ifis the resulting graph by conducting an extending 2-wheel (or 3-wheel) operation, then the minimum degree ofis 2 or 3. We continue to implement an extending wheel operation on, and denote the resulting graph by. If, we refer to these two consecutive extending wheel operations as a domino extending wheel operation;

3.2 Domino extending-contracting operations with inner verticesand domino configuration

Remark Domino configurationsinduced by extending 25-wheel, 34-wheel and 35- wheel operations respectively are isomorphic.

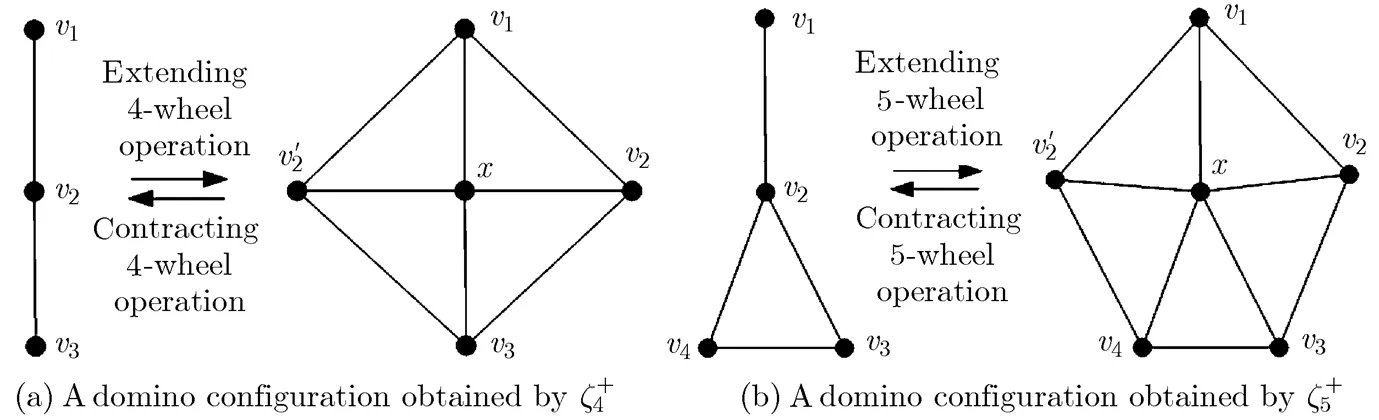
Fig. 10 Two domino configurations with one vertex inside the infinite face

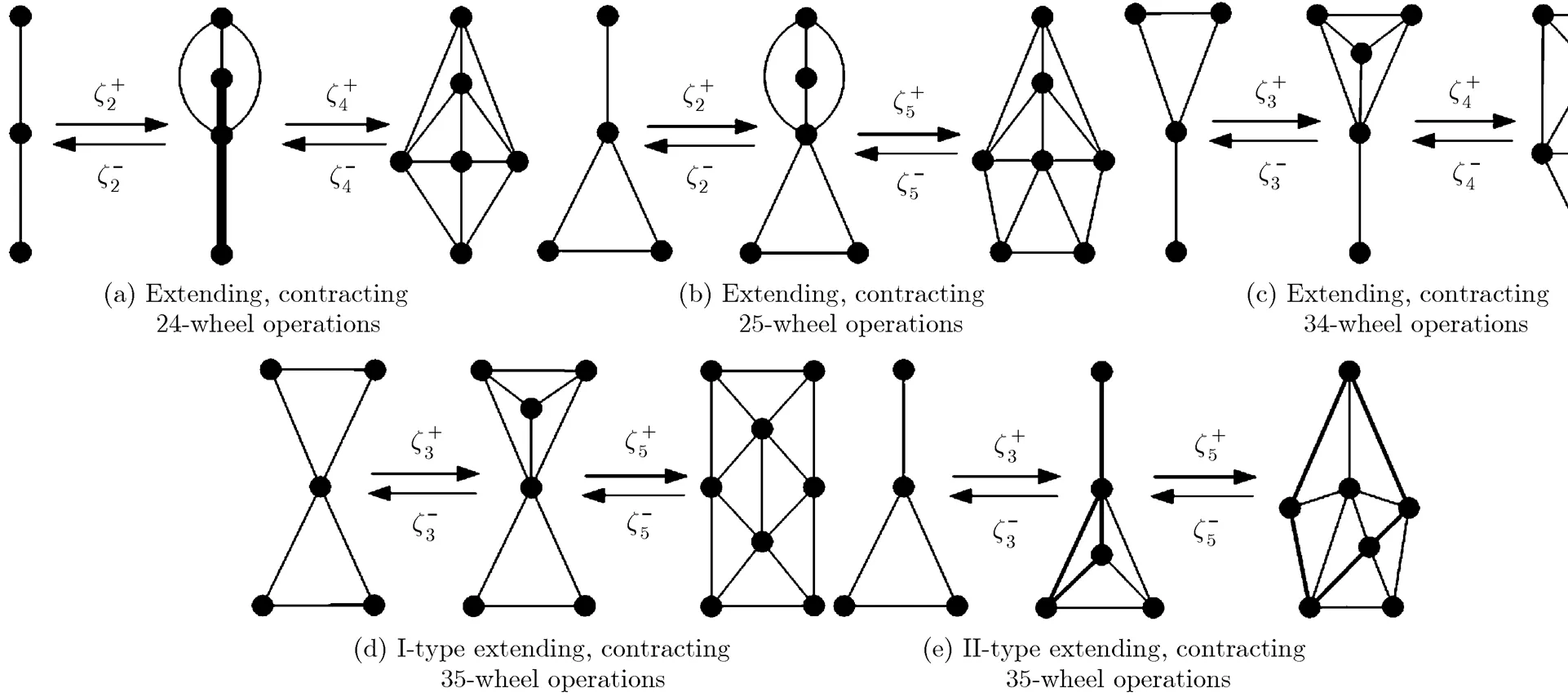
Fig. 11 Domino configurations with two vertices inside the infinite face

Therefore, the number of domino configurations including two wheel-centers is 3.

Analogously, the number of domino contracting wheel operations that involve two wheel-centers is in total five: contracting 24-wheel operation, contracting 25-wheel operation, contracting 34-wheel operation, I-type contracting 35-wheel operation, and II-type contracting 35-wheel operation, respectively; see Fig. 11. It is not hard to obtain the necessary conditions for implementing these five kinds of domino contracting wheel operations. For example, the necessary condition for implementing contracting 24-wheel operation is all vertices in the outer cycle of the corresponding configuration have degree at least 6, except two ones which are identified in the process of contracting 4-wheel operation.

Remark Domino configurations induced by extending 334-wheel and 235-wheel operations are isomorphic, by extending 234-wheel and 335-wheel operations are isomorphic. Therefore, the number of domino configurations that contain three wheel- centers is 7.

Similarly, there are 9 kinds of domino contracting wheel operations involving three wheel- centers: contracting 224-wheel operation, contracting 234-wheel operation, non-adjacent contracting 334-wheel operation, adjacent contracting 334-wheel operation, adjacent

contracting 235-wheel operation, non-adjacent contracting 235-wheel operation, non-adjacent contracting 335-wheel operation, asymmetric and adjacent contracting 335-wheel operation, symmetric and adjacent contracting 335-wheel operation; see Fig. 12. The necessary conditions for implementing these operations can also be deduced easily, so we are not going to repeat them in detail.

To sum up, there are in total a number of 12 domino configurations with 1~3 wheel-centers. For convenience, we list all of them in Fig. 16. In what follows, the wheel-centers in a domino configuration are also called inner vertices of the domino configuration, and the 5 domino configurations illustrated in the first two lines in Fig. 17 are also called basic domino configurations.

3.3 The set of objects of domino extending wheel operations

Based on these three remarks, it is easy to know that there are in total 6 objects in domino extending wheel operations; see Figs. 13(a)~ 13(f).

3.4 General definition of domino configurations

In Subsection 3.2, we showcased all domino configurations containing 1~3 inner vertices. A question naturally arises: what is the structure of a domino configuration when it containsinner vertices? To answer this question, we give a general definition of the domino configuration, and characterize properties of such a class of graphs in this subsection. First, we give three examples to illustrate the processes of domino contacting wheel operations on domino configurations withinner vertices, shown in Fig. 14.

Note that for any domino configuration with 1~3 inner vertices given in Subsection 3.2 or more than 3 inner vertices obtained by implementing domino extending wheel operation, there are the following properties. At least one of 4-wheelor 5-wheelin the domino configuration satisfy: (1) letbe the wheel-center ofor, then there exists a pair of non-adjacent verticesonsuch that; (2)when conducting one domino contracting wheel operation onor, in whichare identified, we can obtain a 2-path, funnel or dumbbell.

Based on the above discussions, we introduce the general definition of domino configurations as follows. Letbe a maximal planar graph with minimum degree at least 4, andbe a semi- maximal planar subgraph ofwith outer cycle. We calla domino configuration if there exists a 4-wheelor a 5-wheelinsatisfying: (1)letbe the wheel-center ofor. Then there exists a pair of non-adjacent verticesonsuch that; (2)when conducting a domino contracting wheel operation onor, in whichare identified, we can obtain a graph without any wheels. Here, we callthe contracted vertices of, and callthe initial contracted wheel-center of.

It is easy to see that every domino configurationcan be contracted into a 2-path, a funnel or a dumbbell subgraph, which implies that the length ofis 4, 5 or 6. So, we have the following theorem.

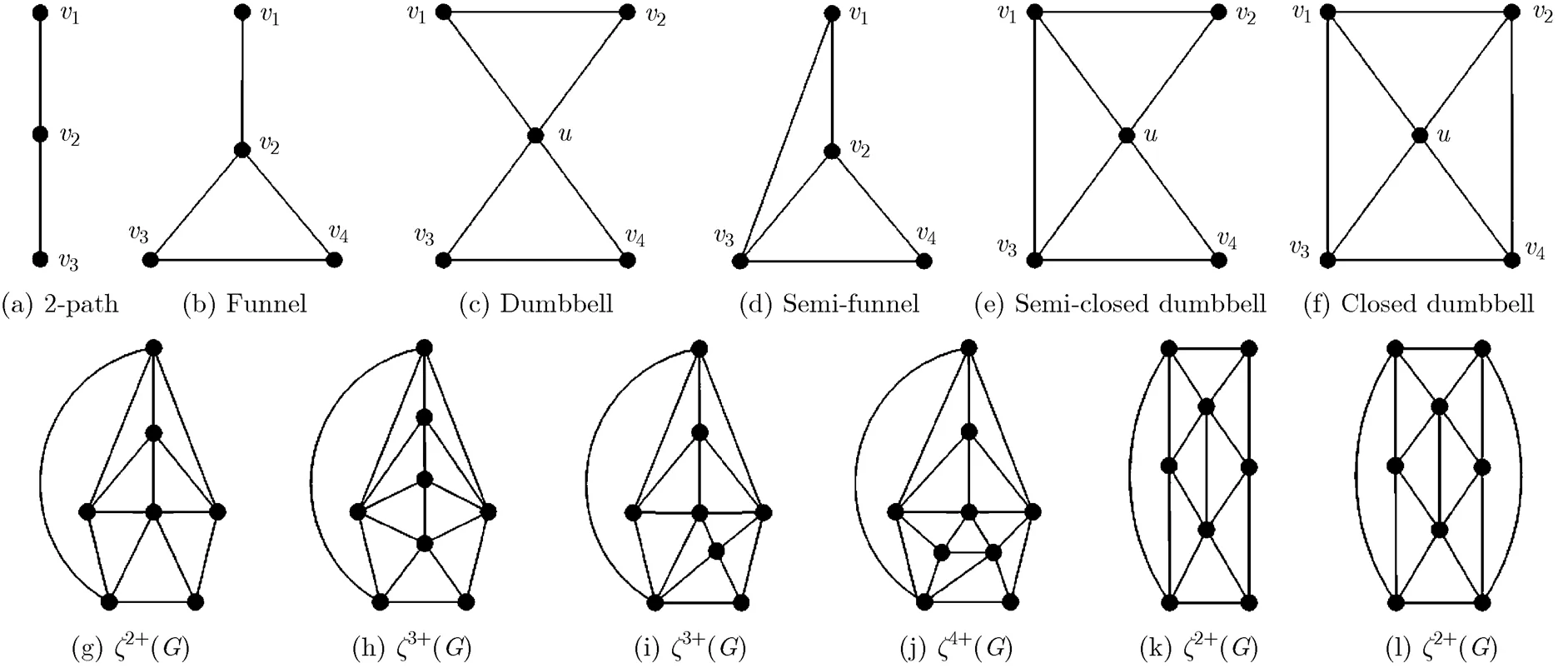
Fig. 13 Sixobject subgraphs that are extended in domino extending wheel operations and examples

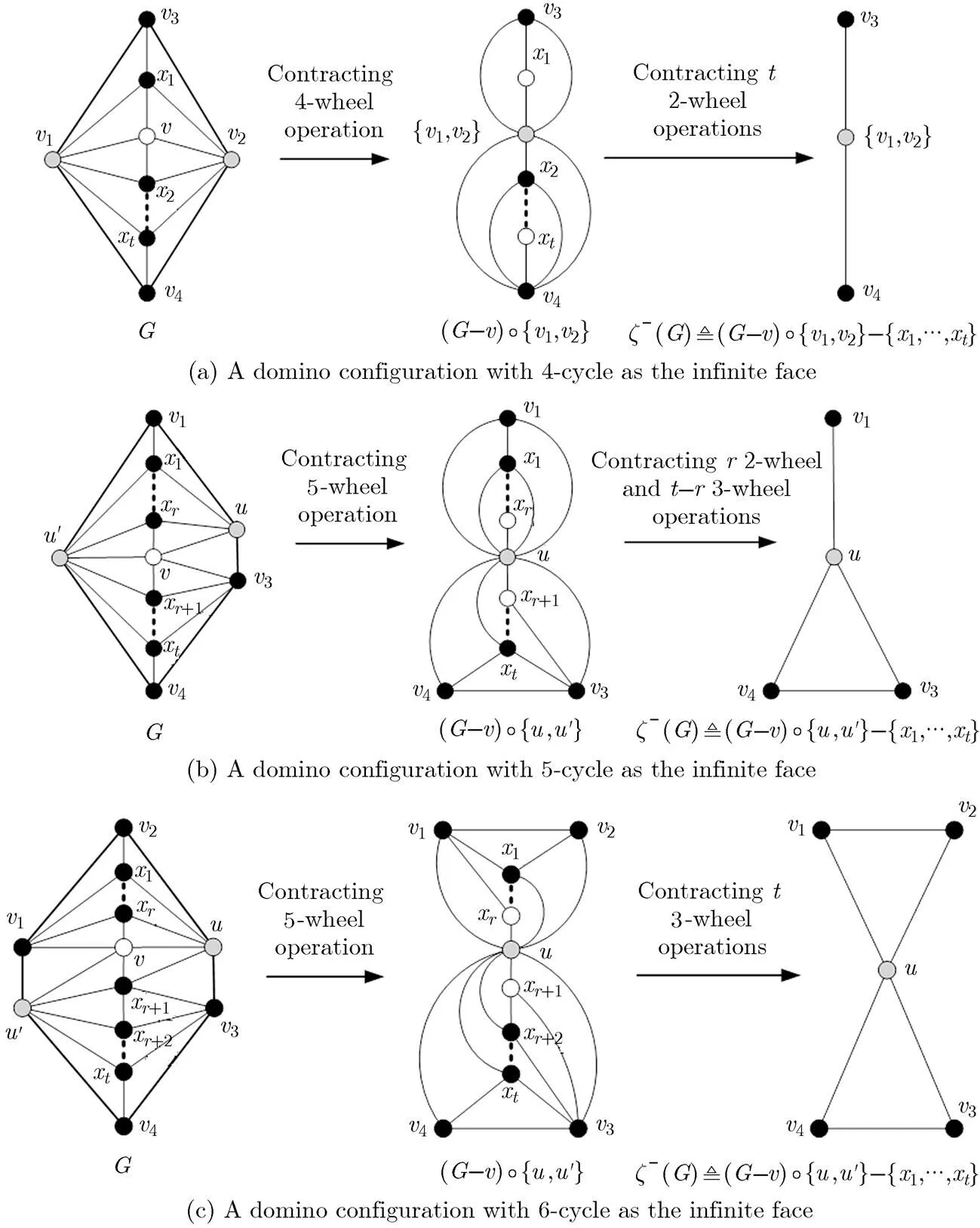
Fig. 14 Three domino configurations with inner vertices

funnel, or a dumbbell subgraph by conducting a domino contracting operation whereare contracted vertices;

Based on Theorem 2, we further have the following result.

Proof For (1), to the contrary we assume

initial contracted wheel-center of. Thencan be contracted into a 2-path by conducting a domino contracting operation. It is easy to see that all degrees ofarein. Suppose that in the process of the above domino contracting wheel operationis the first vertex into be contracted. We useto denote the graph just before the wheel with wheel-centeris contracted during the domino contracting wheel operation. Whenor, it has thatoris adjacent toin, whereis the new vertex after identifyingand. Thus,is adjacent to,

For (2), we present an analogous proof of that for (1).We have that. Obviously,and. Assume thatand. Letbe theneighbors ofor, one by one in, whereis the common neighbor ofand,,. Then in, the

For (3), analogously to the proof of (2), we can deduce thator,or. So the result holds.

Theorem 3 follows from Lemma 1 directly.

configuration with initial contracted wheel-centerand contracted vertices.

3.5 Properties of domino configurations

In order to characterize domino configurations,

we first introduce four operators,,,,,

called generated operations of domino configurations.

Based on the above four operators, we built an operational system to generate domino configurations, denoted by, where. This system aims to generate all domino configurations based onandby using,,,repeatedly. For example, starting with, we can obtain, shown in Fig. 16(a) by implementingsuccessively; starting with, we can obtain

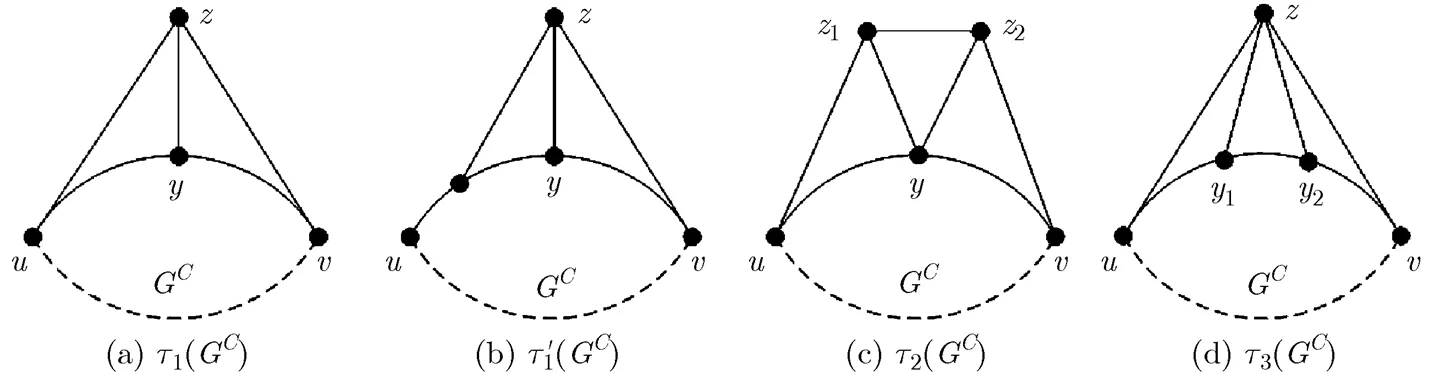
Fig. 15 Four kinds of generated operations of domino configurations

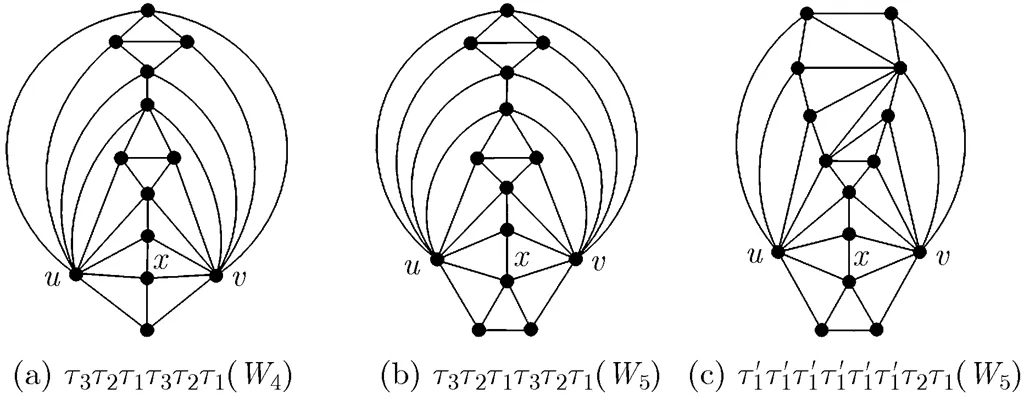
Fig. 16 Threedomino configurations

Note that for any configurationwith the contracted vertices, there exist the following facts.

Theorem 4 Any domino configuration can be generated by.

Proof The proof is by inducing the numberof inner vertices of a domino configuration.

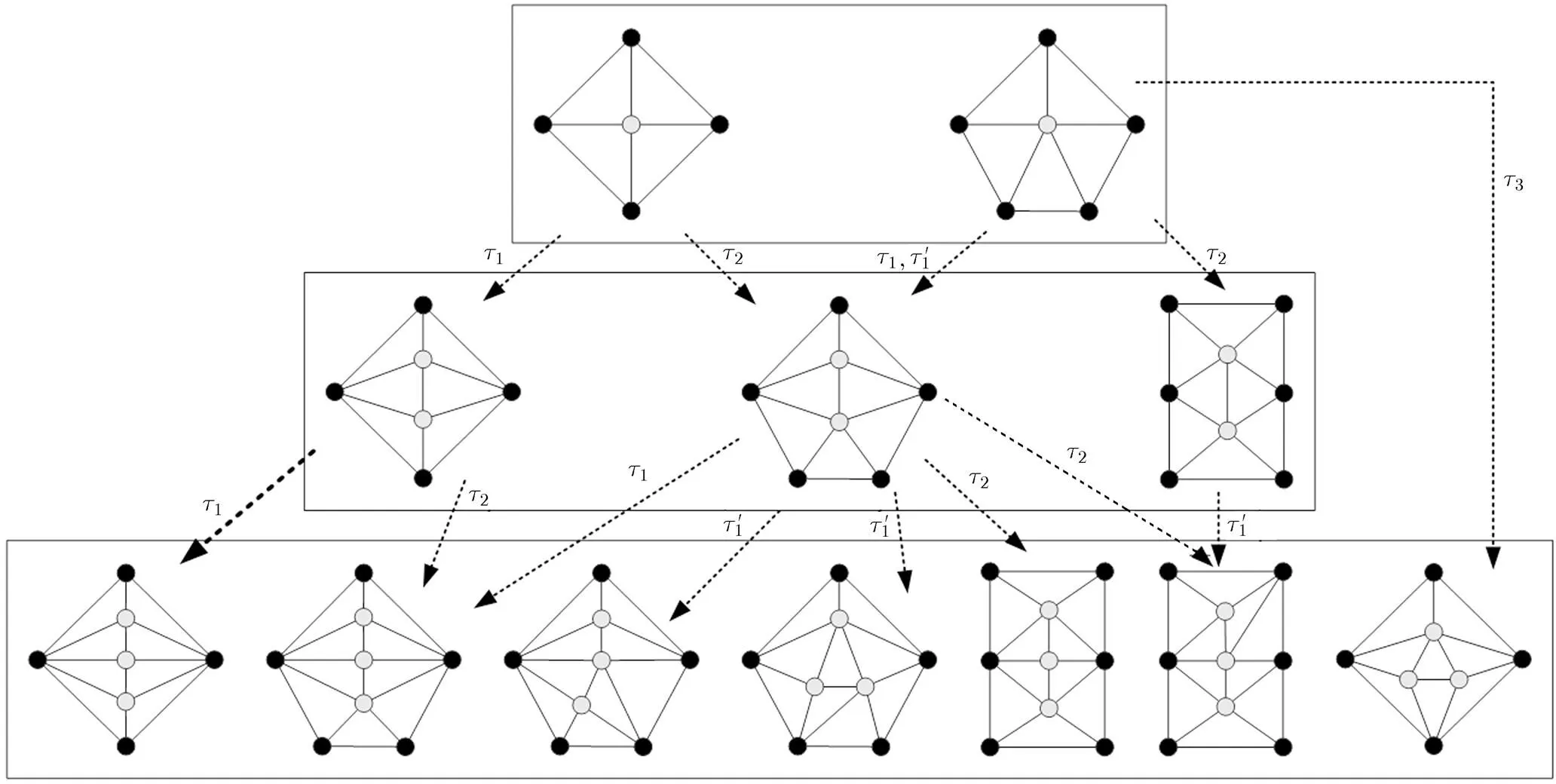
Fig. 17 All the domino configurations with 1~3 inner vertices

domino configuration (in line 3 of Fig. 17) which contain three inner vertices.

In Fig. 17, we get the first and second domino configurations (in line 3) with three inner vertices by conductingandto the first graph in line 2. In addition, we can get the second, third, fourth, fifth, and sixth domino configurations (in line 3) with 3 inner vertices by implementing operations,,,, andon the second graph in line 2, respectively. Note that in the process of these operations, the involved contracted vertices are different. If we conducton the third graph in line 2, then we can also obtain the sixth graph in line 3.

Suppose that the result holds for(). We now consider the case of. Letbe the contracted vertices of. According to Lemma 1, we need to consider the following three cases.

Without loss of generality, we assume thatis not adjacent to the initial contracted wheel-center,

Hence, the conclusion holds.

Theorem 4 provides a method for generating domino configurations, by which any given domino configuration can be generated from. The domino configuration is the core of extending- contracting operational system of maximal planar graphs.

4 Ancestor-graphs and Descendent-graphs

In regard to the construction of maximal planar graphs, we need to consider two basic problems. (1)Where is a maximal planar graph from? More specifically, given a maximal planar graph, what are the characteristics of the maximal planar graphs generatingby using extending wheel operation? (2)How many non- isomorphic maximal planar graphs can be generated from a given one? In order to solve these two problems, we need to use Theorem 4 as a key technique. For this, we introduce the concepts of ancestor-graphs and descendent-graphs.

4.1 Descendent-graphs

outer cycles’ length 4, 5 and 6, respectively, whereare the contracted vertices of. Similarly, descendent-graphs ofare classified into the following three types.

(1)Path-type descendent-graphs

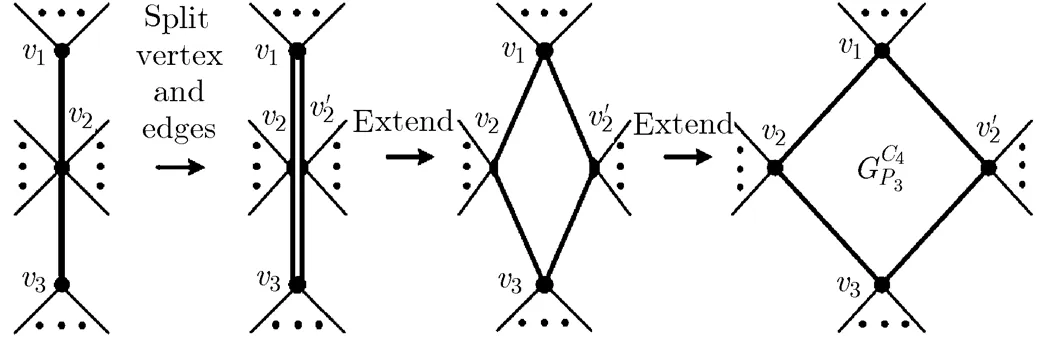
Fig. 18 The process of constructing an extending

-4-cycle-type semi-maximal planar graph

(2)Funnel-type descendent-graphs

(3)Dumbbell-type descendent-graphs

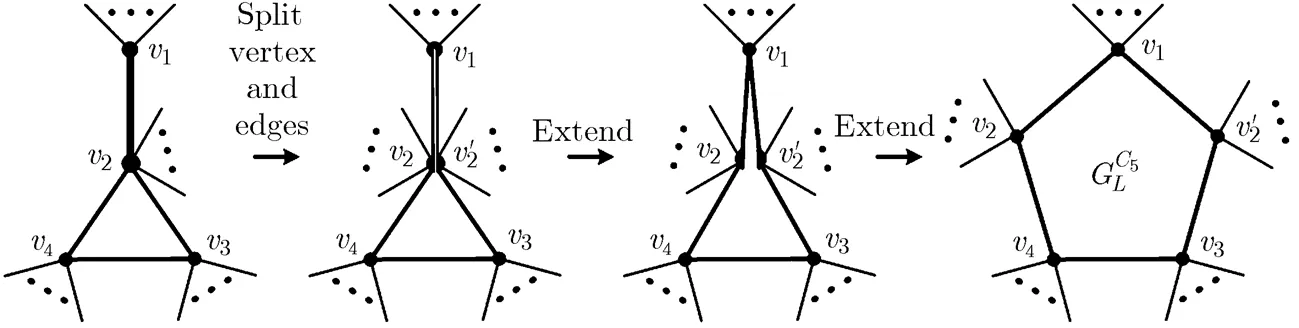
Fig. 19 The process of constructing an extending-5-cycle-type semi-maximal planar graph

This process is shown in Fig. 20, whereandare called extended vertices of.

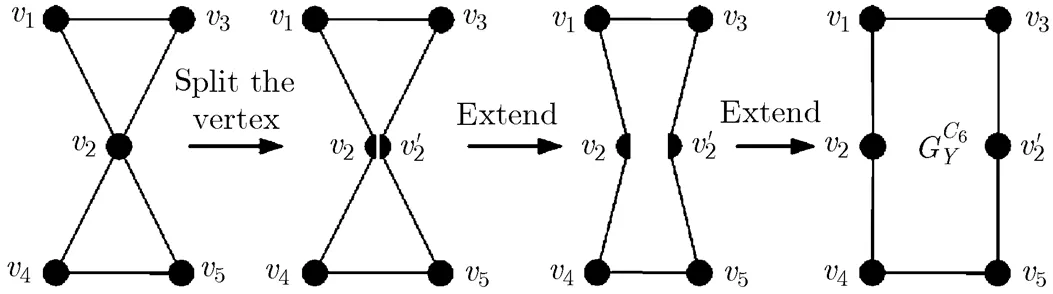
Fig. 20 The process of constructing an extending

-6-cycle-type semi-maximal planar graph

We collectively refer to the three types of descendent-graphs as descendent-graphs. Without taking the length of outer cycle into account, we also call the process of deriving a descendent-graph from a graph as embedding a domino configuration in an extending-cycle-type semi-maximal planar graph. By the discussion in the last section, we have that

The above formula means that every maximal planar graphwithhas infinite amount of descendent-graphs. So the descendent- graphs ofcan be classified by the number of inner vertices of domino configurations. Generally, if there areinner vertices in the domino configuration, then we call the corresponding descendent-grapha-th descendent-graph of, and useto denote the set of all-th descendent-graphs of. Particularly, the 1-st, 2-nd and 3-rd descendent-graphs are also called the son-graph, grandson-graph, and great-grandson- graph, respectively.

Throughout this paper, we denote bythe set of all non-identical subgraphs ofIn particular, we use,,,,andto denote the sets of all non-identical 2-path, funnel subgraph, semi-funnel subgraph, dumbbell subgraphsemi-closed dumbbell subgraphand closed dumbbell subgraphof, respectively.

4.2 Ancestor-graphs

configuration with contracted vertices, and the subgraph ofinduced byand its

interior is a domino configurationwith contracted vertices, andin whichis the semi-

maximal planar graph consisting ofand its exterior, then werefer toas the ancestor-graph ofbased on, or the dumbbell-type ancestor-graph of.

When ignoring the length of outer cycle of domino configurations, the above three types of ancestor-graphs are collectively called ancestor- graphs.

Remark For a maximal planar graphwith, different from its descendent-graphs, there is only one ancestor-graph based on a given domino configuration.

the 1-st, 2-nd and 3-rd ancestor-graphs are also called the father-graph, grandfather-graph, and great-grandfather-graph, respectively.

As an illustration, we take the icosahedron for instance (see the graph of order 12 and degree sequence 555555555555 shown in Appendix B). Since icosahedron contains only one non-identical domino configuration, the 5-wheel, it follows that icosahedron has only one ancestor-graph according to Theorem 5; see Fig. 21(a).

In addition, by Equation (6), we can see that icosahedron contains one non-identical 2-path, one

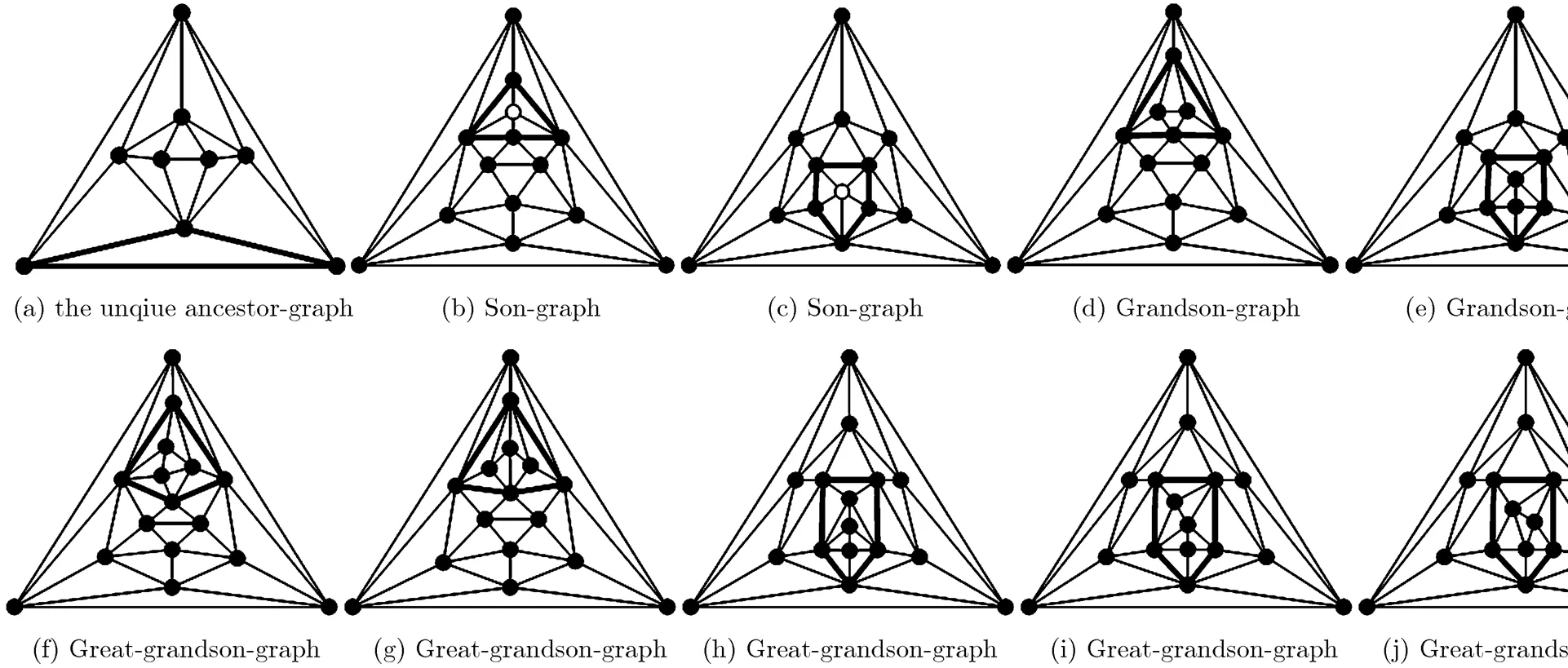
Fig. 21 The icosahedron together with its ancestor-graph and the 1~3rd descendent-graphs

non-identical funnel subgraph and no dumbbell subgraph. Therefore, according to Fig. 17 and discussions in Subsection 4.1, it has that the number of the 1~3rd descendent-graphs of icosahedron is 9; see Figs. 12(b)~12(j).

5 Methods to Generate Maximal Planar Graphs

The previous two sections give methods to construct ancestor-graphs and descendent-graphs of a maximal planar graphwith. This section is devoted to considering how to construct a maximal planar graph of order. First, we prove that every maximal planar graph can be generated from another one by a sequence of extending wheel operations, in other words, by some domino extending wheel operations. Then we describe how to construct a separable maximal planar graph. Finally, we show that any maximal planar graph with orderand minimum degreehas an ancestor-graph of orderor.

5.1 General theory on constructing graphs

Proof The proof is by inducing the number. When, there is only one maximal planar graph. So the conclusion is true. Suppose that the conclusion holds for(), which means that any maximal planar graph with order at mostcan be contracted toby implementing contracting 2-wheel, 3-wheel, 4-wheel, and 5-wheel operations, repeatedly.

Now we consider the case when. For any maximal planar graphof order, ifhas a 2-degree or 3-degree vertex, then we will get a maximal planar graph with order,or, by deleting a 2-degree or a 3-degree vertex and its incident edges. According to the induction hypothesis, the conclusion holds. Ifor 5, then properly implementing a contracting 4-wheel operation or a contracting 5-wheel operation for some 4-degree or 5-degree vertex, we will get a graphorwhich is a maximal planar graph of order. On the basis of the induction hypothesis, they can be contracted toby a series of contracting-wheel operations for. Hence, the conclusion holds.

According to Theorem 6, we can see that every maximal planar graph of ordercan be contracted toby implementing four basic contracting wheel operations repeatedly. Accordingly, if we trace back to the reverses of contracting-wheel operations of graph, then by starting withand conducting the corresponding extending-wheel operations,

we can get the original graph. So, the following corollary holds.

Corollary 1 Any two maximal planar graphs can be transformed into each other by implementing the four pairs of contracting and extending operations.

5.2 Construction of separable maximal planar graphs

Remark In the process of relabeling,can also be defined in other ways. For example,,, andcan be relabeled by,, and, respectively. Of course, we will obtain different separable graphs by relabelingin different ways.

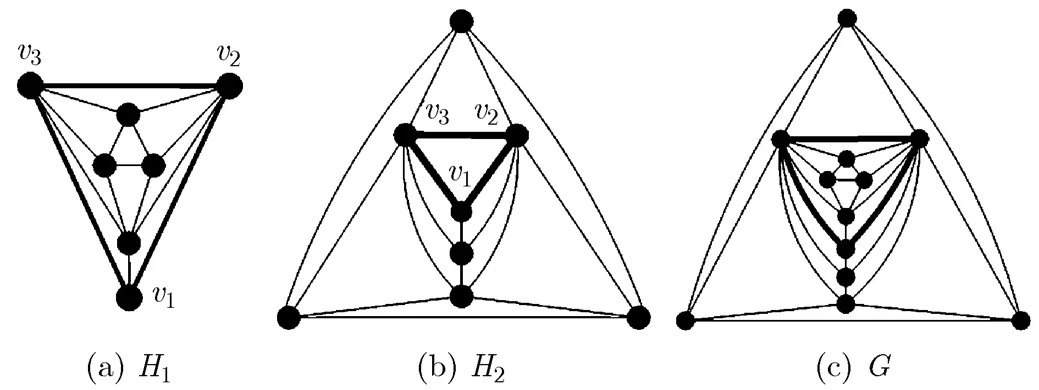
Fig. 22 The process of an embedding operation

to generate a separable graph

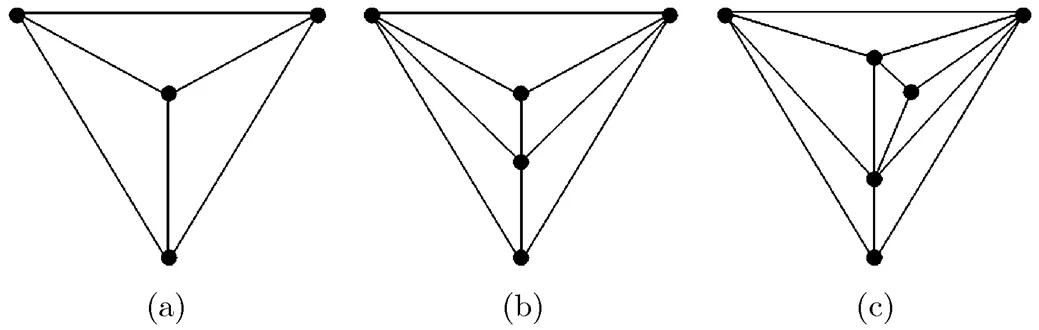
Fig. 23 Three recursive maximal planar graphs

It is easy to prove that every recursive maximal planar graph has at least two vertices of degree 3. A recursive maximal planar graph is called a (2,2)-type recursive maximal planar graph if it contains only two vertices of 3-degree. For example, graphs shown in Figs. 23(b) and 23(c) are (2,2)-type recursive maximal planar graphs. An in-depth research on recursive maximal planar graphs is given in Ref. [24].

It is easy to see that the following result holds.

The smallest maximal planar graph with minimum degreehas six vertices; see the first graph in Appendix B. The smallest maximal planar graph with exactly one 3-degree vertex is the graph shown in Fig. 22(a). Thus, by Theorem 7, the smallest separable maximal planar graph has an order of 9 (). Further, according to Theorem 7, we give a method to generate any separable graph with orderas follows.

In this case, we can construct a separable graph of orderusingandtwo maximal planar graphs with minimum degree at least 4, by the following steps, wherehas order(),.

Step 1 Find out all the non-identical triangle faces ofand, respectively;

Step 2 For every non-identical triangle face of, embed it in every non-identical triangle face of, and the resulting graphs are our desired ones.

Step 1 Find out all the non-identical triangle faces ofand;

Step 3 For any triangle face of, denoted by, implement an embedding operation ofandbased onrespectively. Then, the resulting graphs are the desired ones.

Step 1 Find out all the non-identical triangle faces ofand;

By the above method, we construct all of the two separable maximal planar graphs of order 10 as

follows.

By using this method, we can construct all the nine separable maximal planar graphs of order 11; see the 17, 19, 24~28, 30, 32nd graphs among maximal planar graphs of order 11 in Appendix B. Similarly, all forty-three separable maximal planar graphs of order 12 are also constructed; see the 38, 49~52, 58, 62, 64, 68, 70, 72, 74, 81, 83, 84, 86~94, 98~100, 103, 105, 107, 109, 110, 112, 113, 115~117, 119, 120, 122, 125, 127, 129th graphs among maximal planar graphs of order 12 in Appendix B.

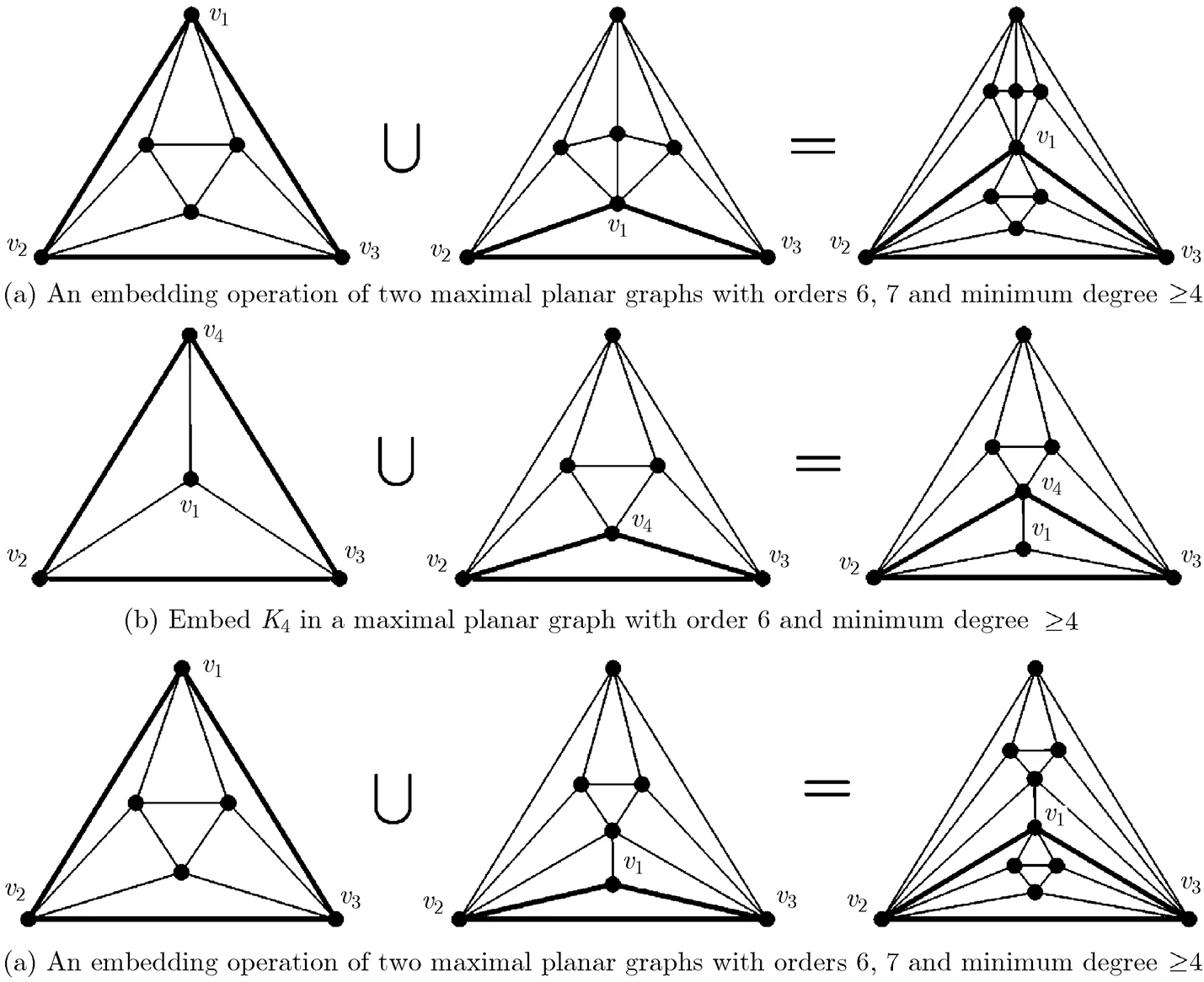
Fig. 24 Processes of constructing two separable maximal planar graphs of order 10

5.3 Basic theorem on constructing non-separable maximal planar graphs of minimum degree

The neighbors of1,2, and3are denoted by1,in clockwise, as shown in Fig. 25(a). We then further deal with three cases as follows.

The neighbors of1,2, and3in this situation are shown in Fig. 25(e).

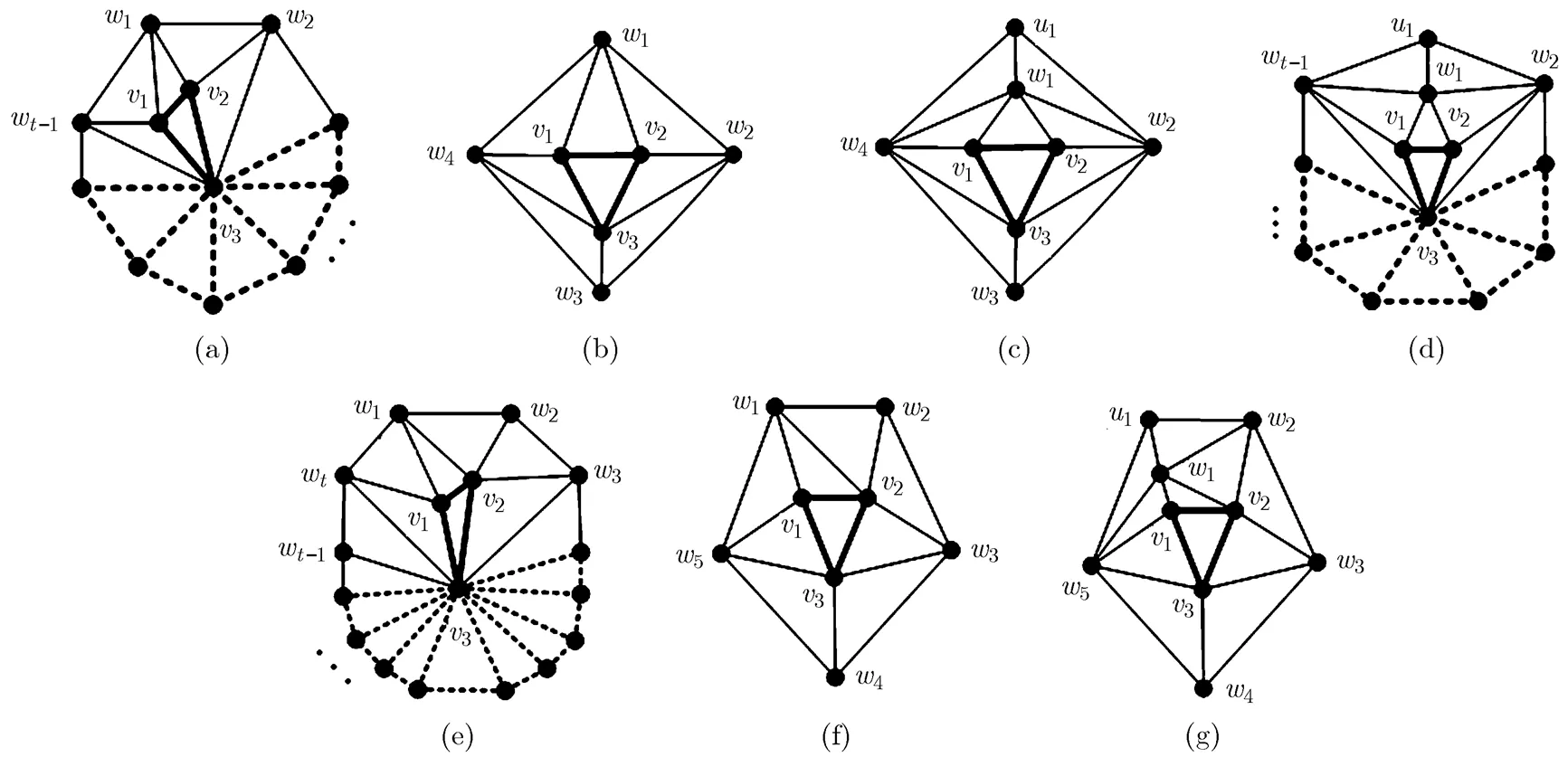
Fig. 25 The schematic for the proof of Theorem 8

Hence, the theorem holds.

5.4 A recursive method to generate non-separable maximal planar graphs with orderand minimum degree

Based on the Theorem 8, this section will present an approach to construct non-separable maximal planar graphs recursively. Suppose thatis the set of all non-identical and non- separable maximal planar graphs with orderand minimum degree. Now, we generate all of graphs inby the following.

We illustrate the process of constructing(9) as follows.

Notice that there is only one non-separable maximal planar graph of minimum degreeand order 7, denoted by; see Fig. 26(a). It is easy to see thatand(the bold lines in Figs. 26(a)~26(d)). Thus, if we implement an extending wheel operation on every 2-path inand funnel in, respectively, then we can obtain four maximal planar graphs with order 9 and minimum degree; see Figs. 26~26, in which two graphs shown in Fig. 26and

In addition, one can readily confirm thatcontains only one graph, denoted also by, see Figs. 26(e). This graph has strongly symmetrical

Above all, we construct all of the four non- isomorphism and non-separable maximal planar graphs with minimum degreeand order 9; see Fig. 26 or Appendix B.

By using the methods on how to generate

separable and non-separable maximal planar graphs, prescribed in Subsections 5.2 and 5.4, we construct all of the maximal planar graphs with order 6~12 and minimum degree. These graphs are listed in Appendix B.

6 Conclusion and Prospection

The first paper of this series of articles revealed that the Four-Color Conjecture can be hopefully proved mathematically by investigating a special class of graphs, called the 4-chromatic-funnel pseudo uniquely-4-colorable maximal planar graphs. The 4-coloring of this kind of graphs is closely related to the funnel subgraphs in the graphs. Based on these observations, we introduce the extending-contracting operational system. This system not only correlates with funnel subgraphs naturally, but also associates the structure with 4-coloring of a maximal planar graph closely (see the later paper of this series of articles). This is the essential advantage over the existing methods, and also a novel idea to solve hard problems, such as Four-Color Conjecture, Uniquely Four-Colorable Planar Graphs Conjecture, Nine-Color Conjecture,.

The main contributions of this paper are as follows.

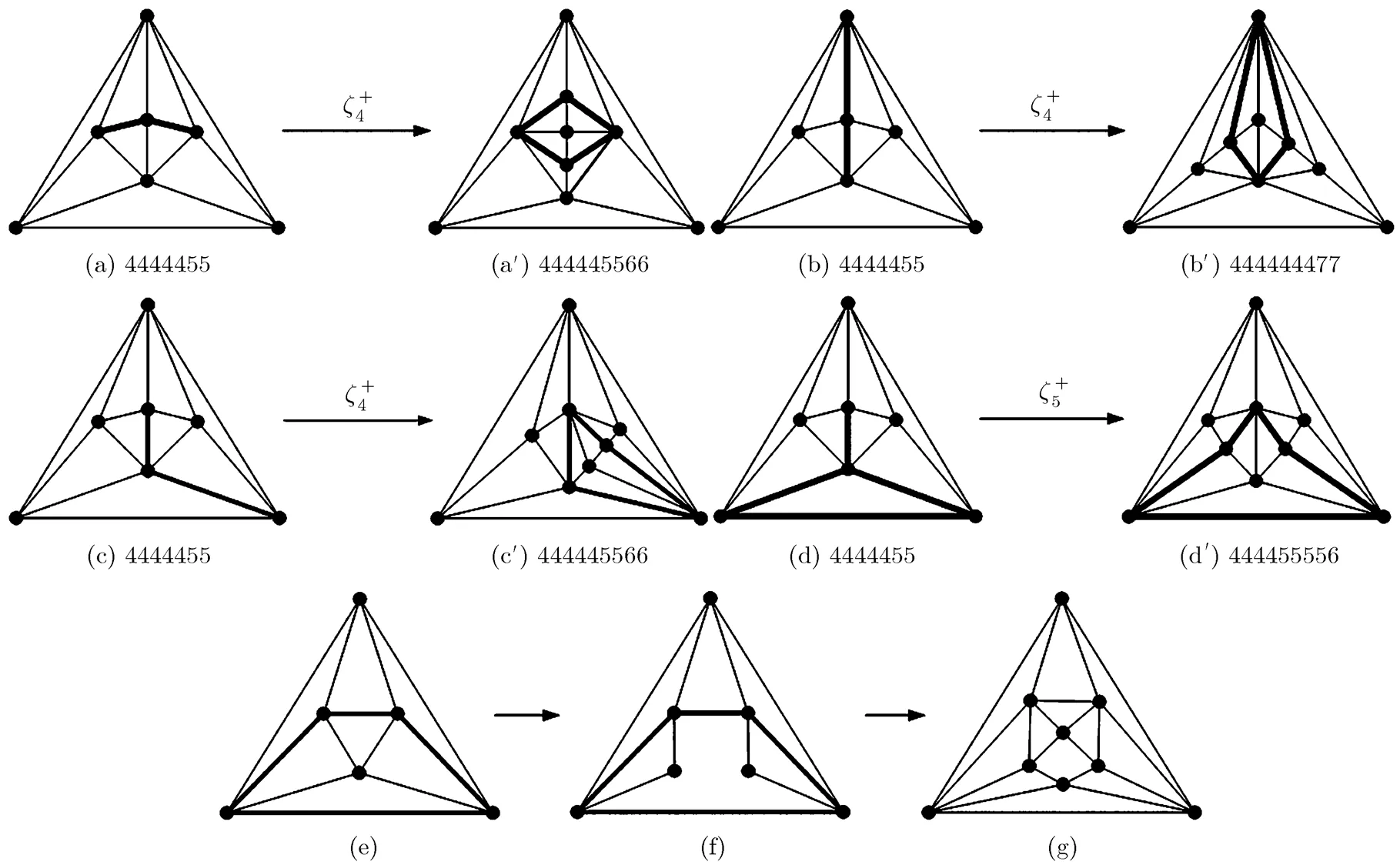
Fig. 26 Procedures of constructing

(1)A new method, called extending- contracting operation, is established to generate maximal planar graphs, which can connect the structure and coloring of an arbitrary maximal planar graph closely.

(2)A useful class of subgraphs in maximal planar graphs of minimum degreeis observed and studied. We characterize the structures of these graphs in depth and propose an approach to construct them. This work is the foundation to construct maximal planar graphs recursively.

(3)We introduce the definitions of ancestor- graphs and descendent-graphs of a maximal planar graph of minimum degree, and propose a method to construct them.

(4)It is proved that every maximal planar graph with order() and minimum degreehas an ancestor-graph of orderor(Theorem 8), based on which a recursive method is given to construct maximal planar graphs of order(). As examples, all maximal planar graphs with order 6~12 and minimum degreeare constructed.

Note that Theorem 8 is the foundation for our subsequent study. Based on the work Shown in this paper, starting from the third paper of this series of articles, we will demonstrate the combination of structures and 4-colorings of maximal planar graphs.

Acknowledgements The author would like to gratefully acknowledge the efforts of discussions with and communications from many colleagues, among them Professors YAO Bing, CHEN Xiangen, WU Jianliang, and my students LIU Xiaoqing, ZHU Enqiang, LI Zepeng, WANG Hongyu, and ZHOU Yangyang. Many thanks to Associate Professor BIAN Kaigui who revised the English version carefully. Finally, I would especially like to thank the Academician HE Xingui and Processor YU Daoheng in Peking University for their reviews, selfless supports and encouragements to accomplish this study.

Appendix A Table of the number of all maximal planar graphs of order 6~23 and minimum degree

In order to verify the main results in Section 5, we need to know the total number of maximal planar graphs with order 6~12 and minimum degree. Here, we count the number of all maximal planar graphs of order 6~23 and minimum degreeby using the algorithm proposed by BRINKMANN and MCKAY[15]in 2007, see the Table A1.

Table A1 The number of all the maximal planar graphs of order 6~23 and minimum degree

Order6789101112 Number11251234130 Order13141516171819 Number52524721240065619357504199298511284042 Order20212223 Number64719885375126827219443939812941995397

Appendix B All the maximal planar graphs of order 6~12 and minimum degree

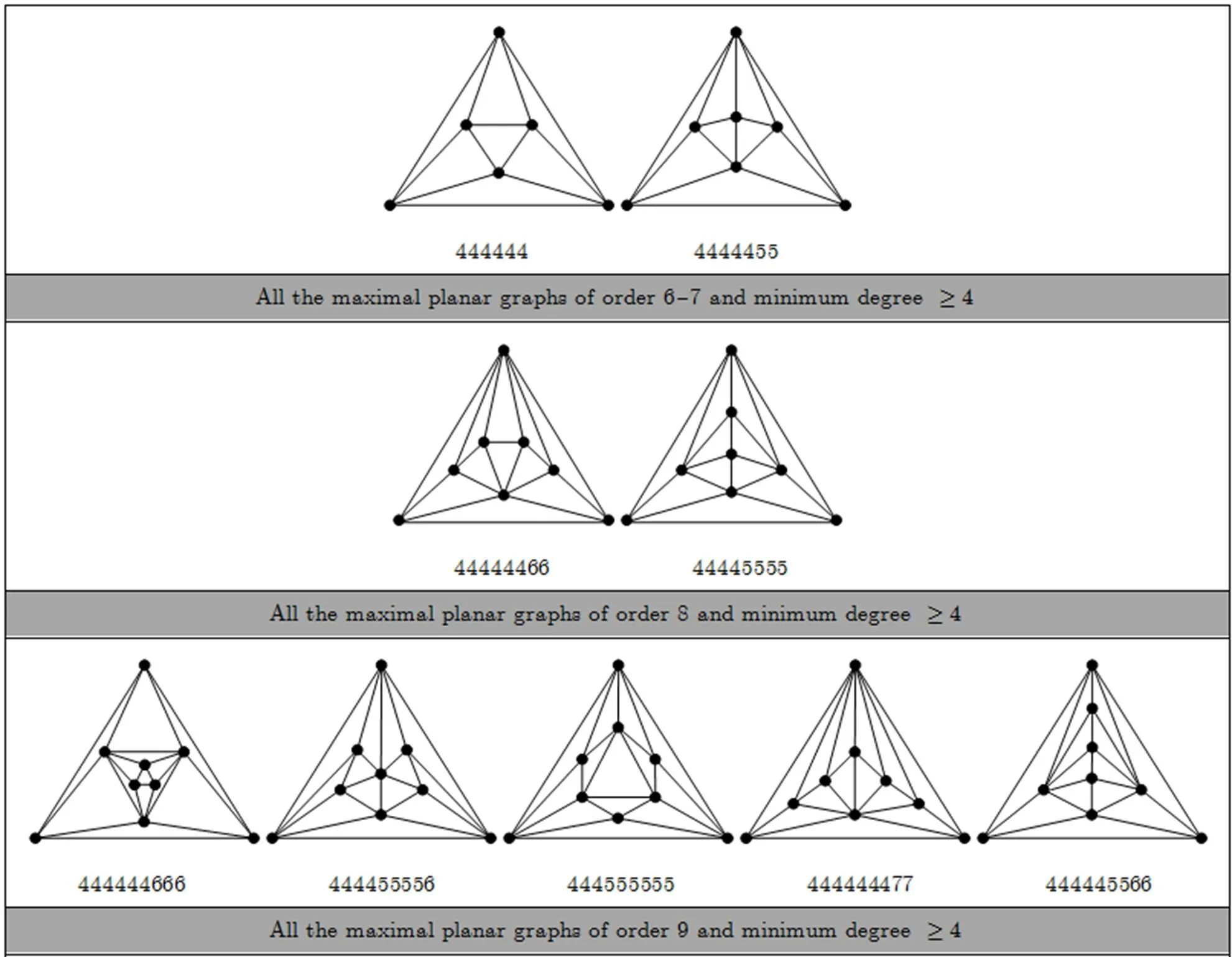
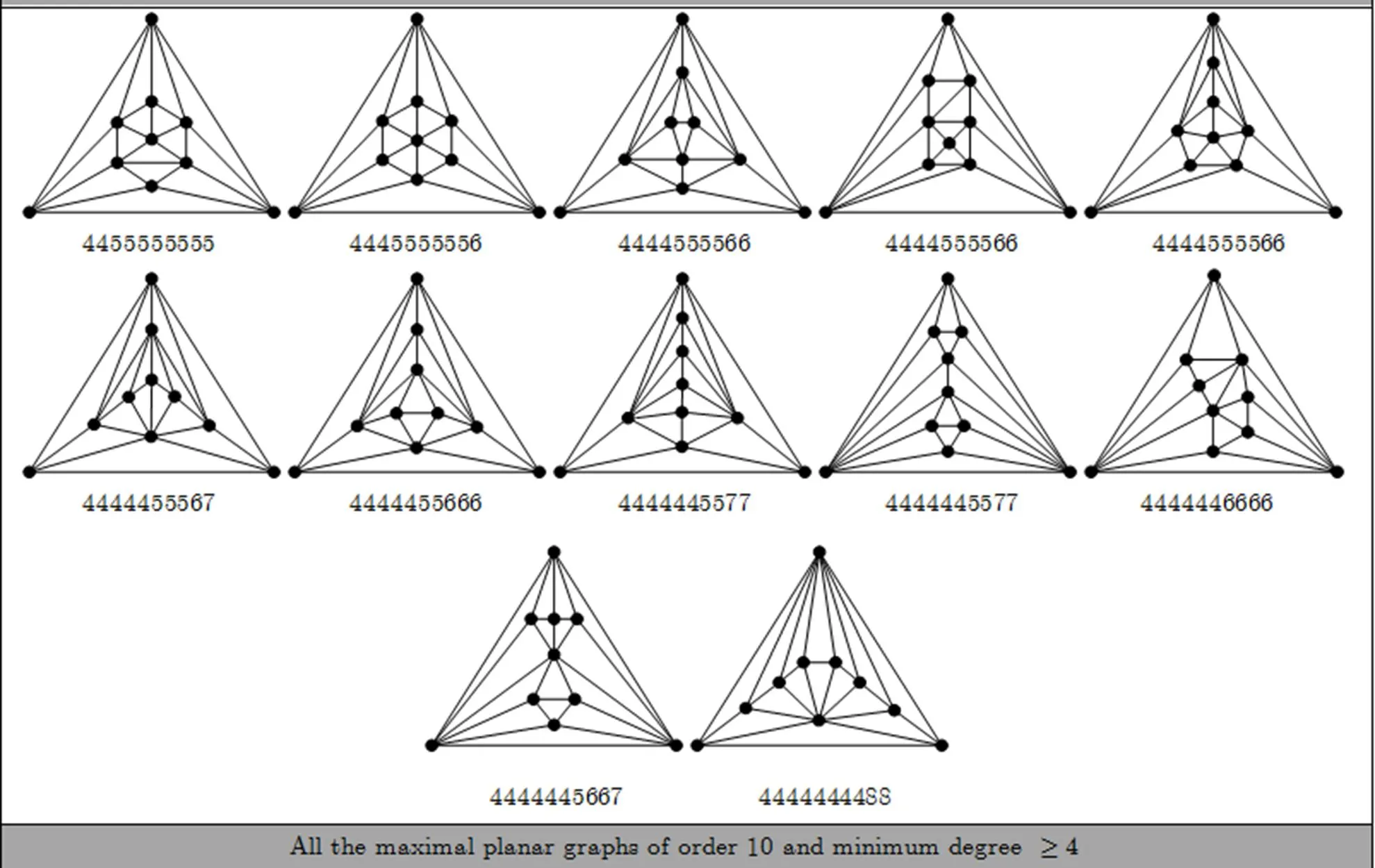
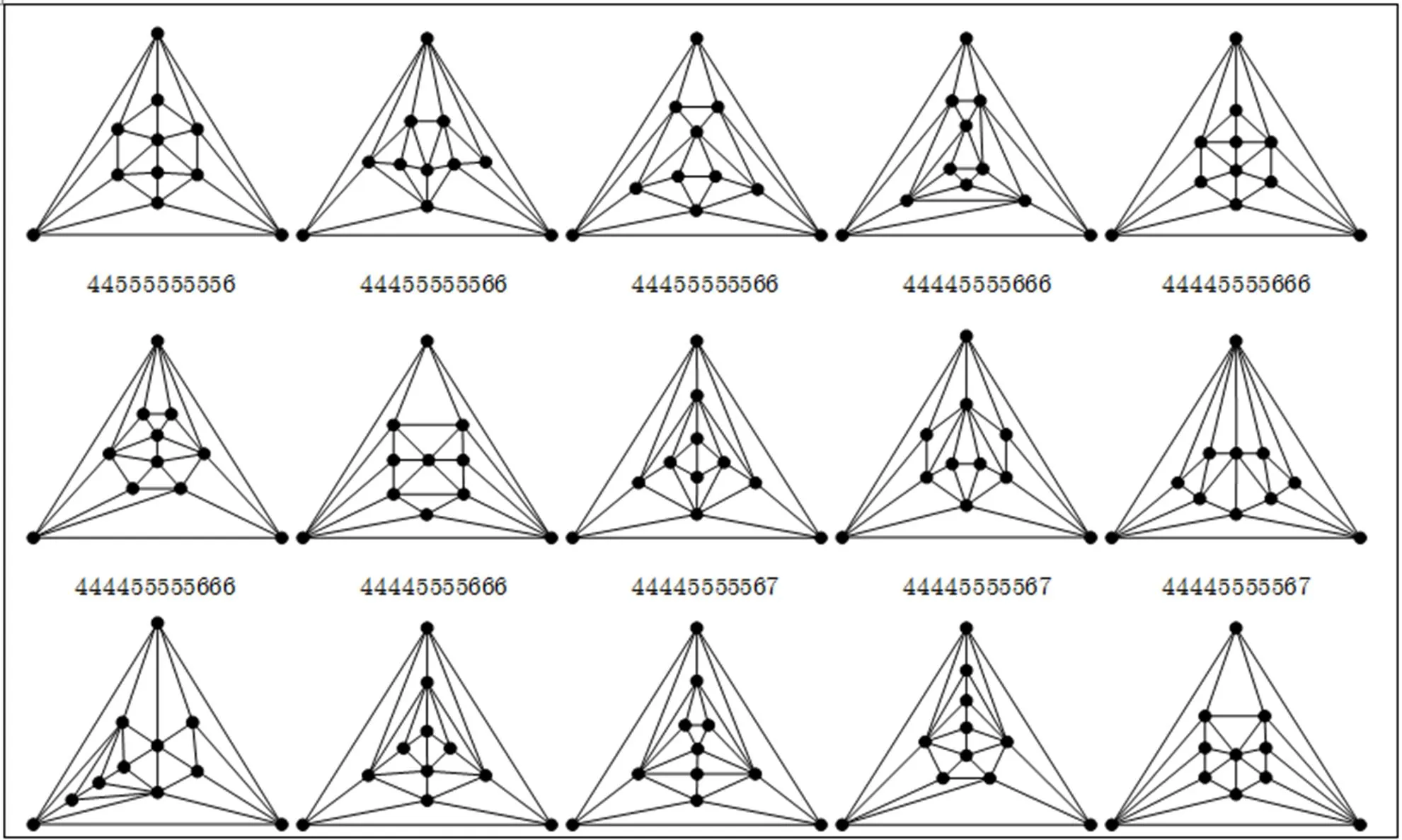
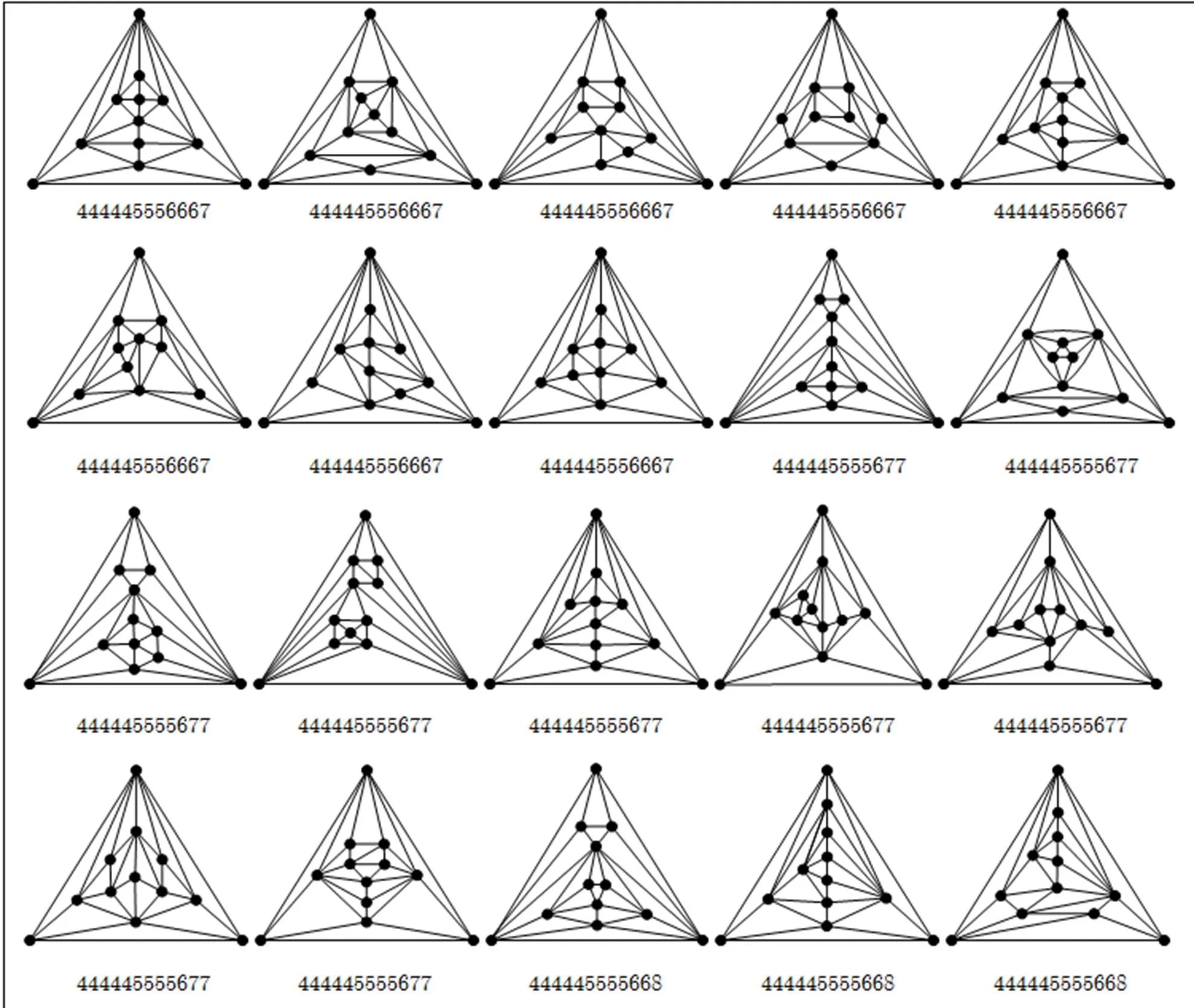
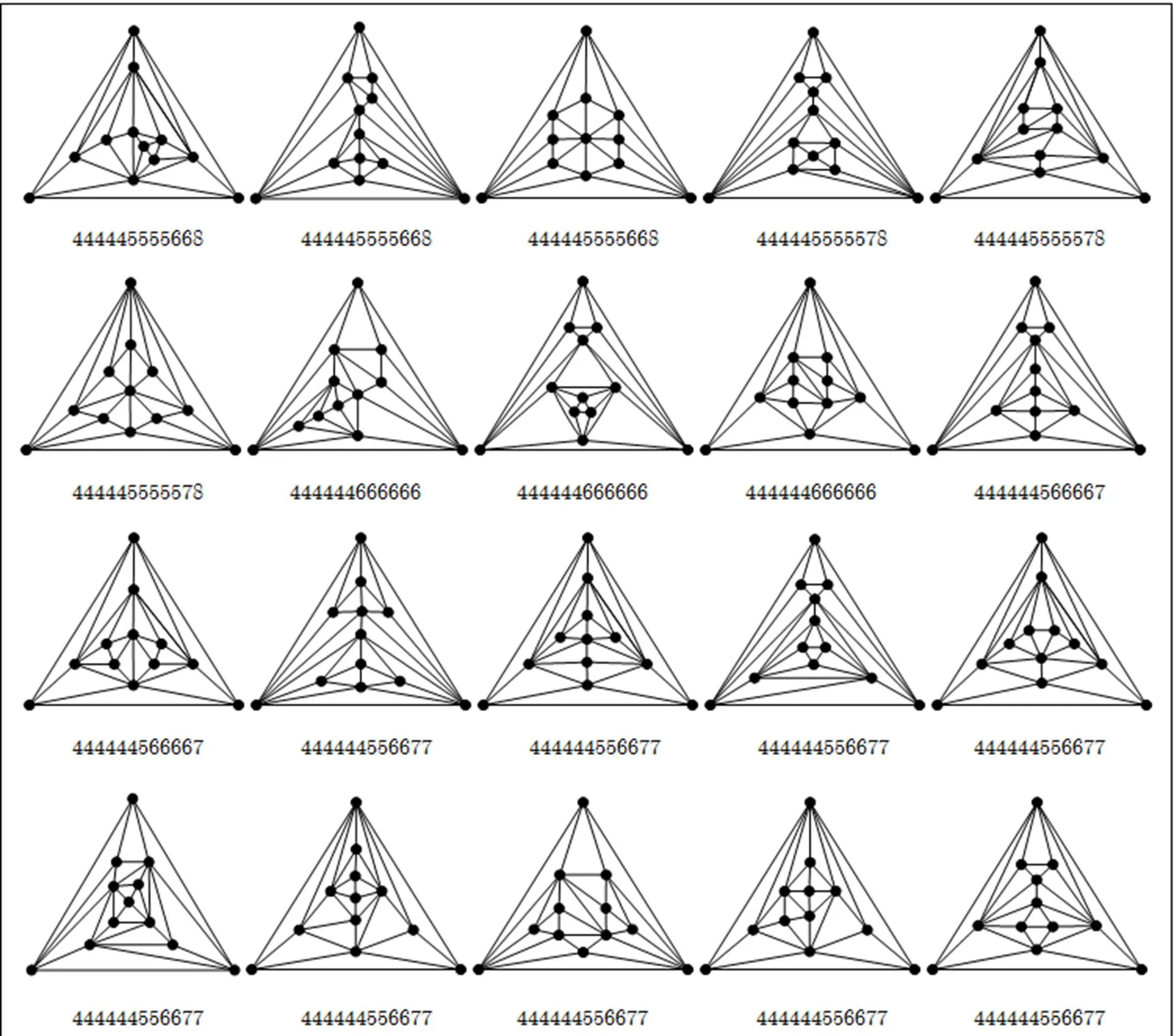
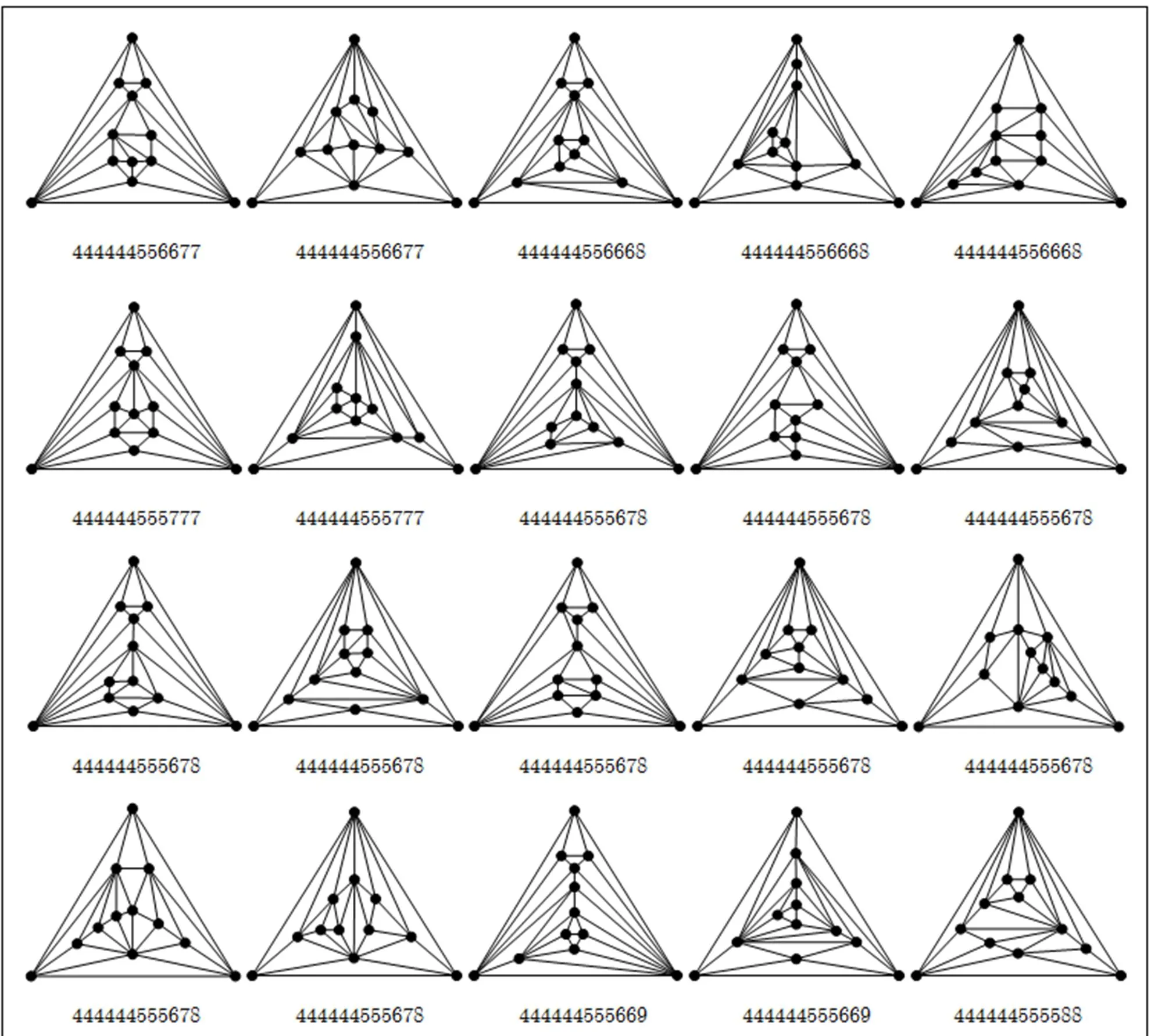
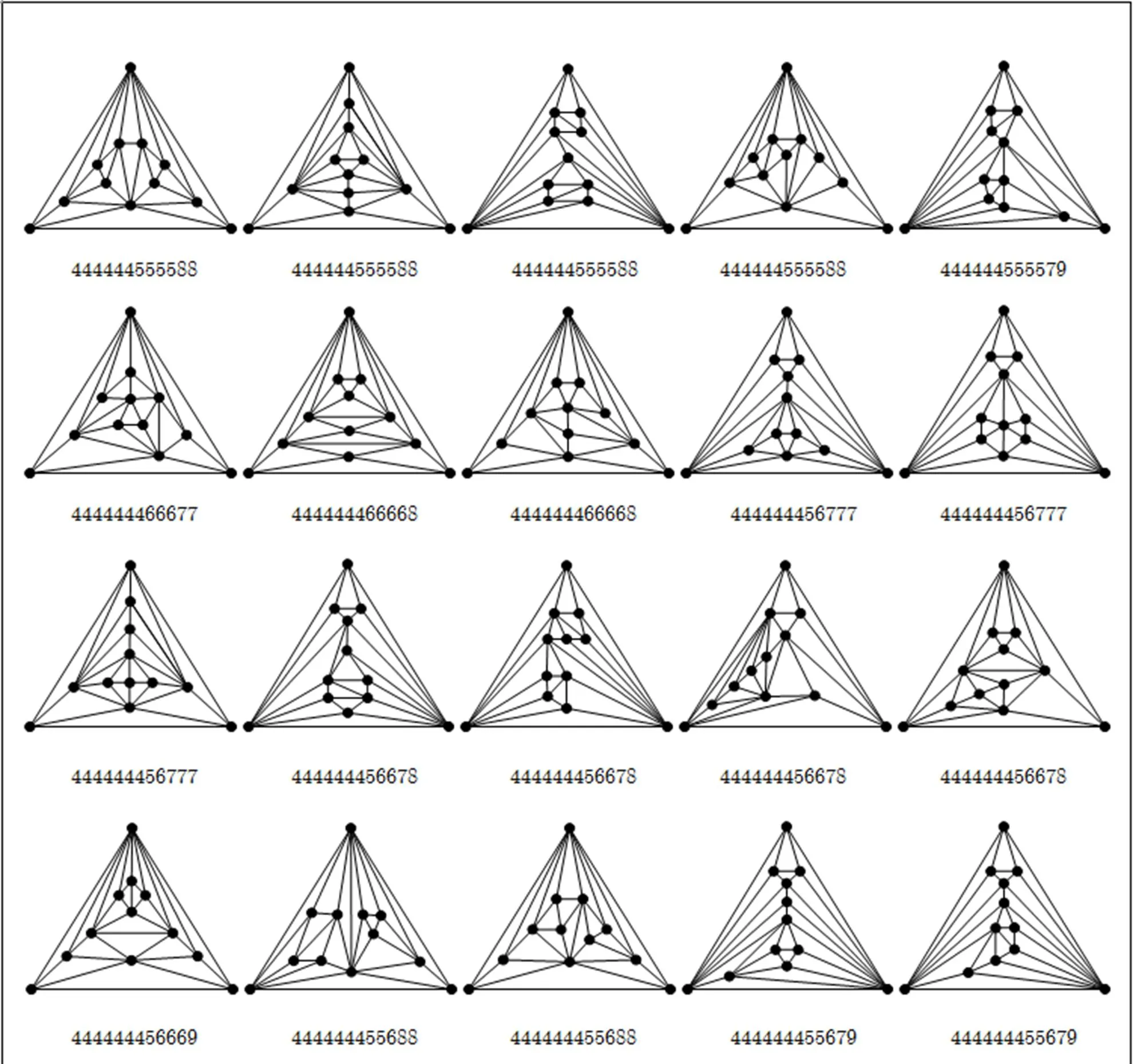
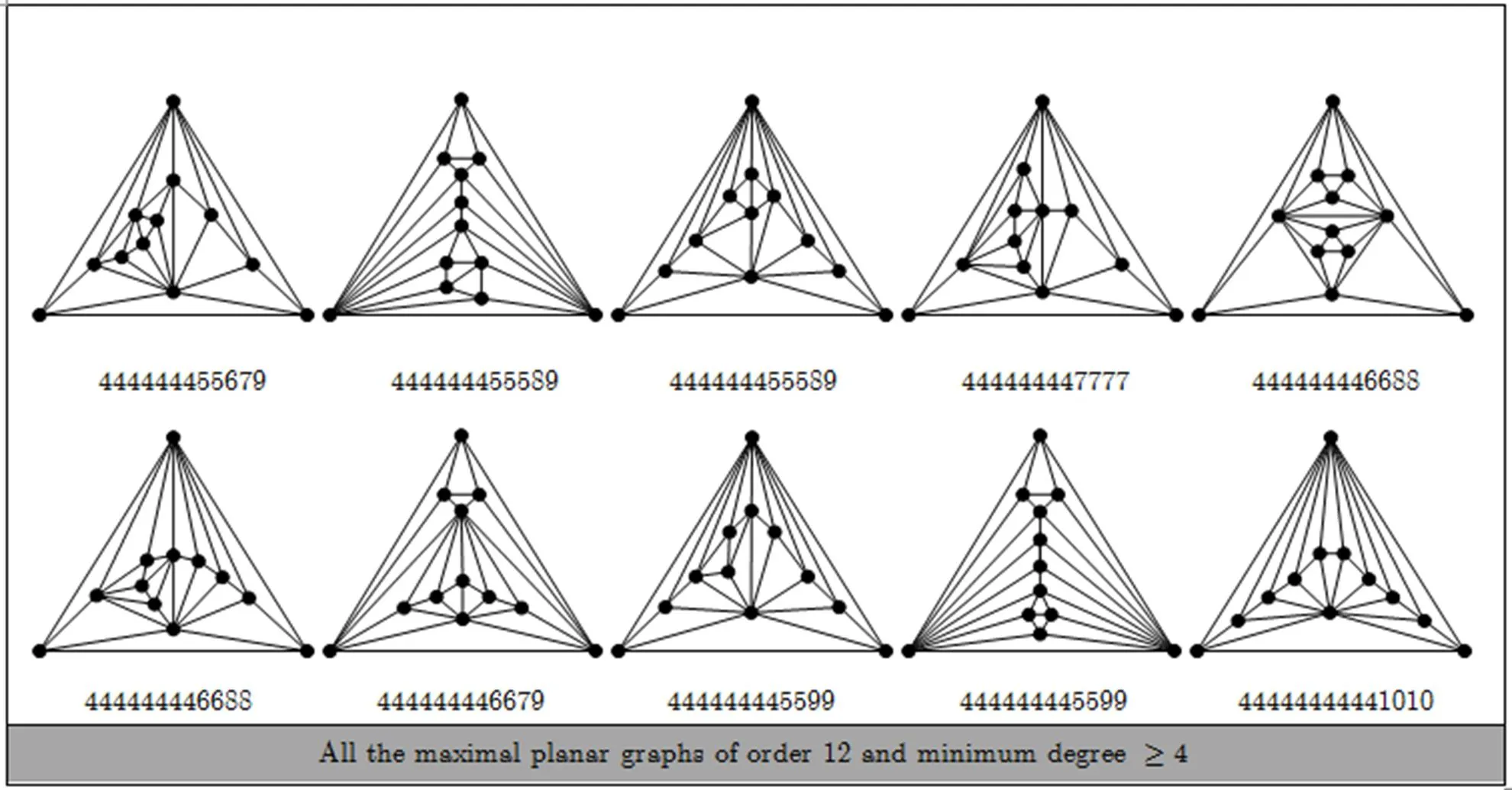
Fig. B1

References

[1] APPEL K and HAKEN W. The solution of the four-color map problem[J]., 1977, 237(4): 108-121. doi: 10.1038/scientificamerican1077-108.

[2] APPEL K and HAKEN W. Every planar map is four colorable, I: discharging[J]., 1977, 21(3): 429-490.

[3] APPEL K, HAKEN W, and KOCH J. Every planar map is four-colorable, II: Reducibility[J]., 1977, 21(3): 491-567.

[4] EBERHARD V. Zur Morphologie Der Polyeder, Mit Vielen Figuren Im Text[M]. Leipzig: Benedictus Gotthelf Teubner, 1891: 14-68.

[5] 王邵文. 構(gòu)造極大平面圖的圈加點法[J]. 北京機械工業(yè)學(xué)院學(xué)報, 2000, 15(1): 26-29.

WANG Shaowen. Method of cycle add-point to construct a maximum plate graph[J]., 2000, 15(1): 26-29.

[6] 王邵文. 構(gòu)造極大平面圖的三種方法[J]. 北京機械工業(yè)學(xué)院學(xué)報, 1999, 14(1): 16-22.

WANG Shaowen. Three methods to construct maximum plain graph[J]., 1999, 14(1): 16-22.

[7] BARNETTE D. On generating planar graphs[J]., 1974, 7(3-4): 199-208. doi: 10.1016/0012- 365X(74)90035-1.

[8] BUTLER J W. A generation procedure for the simple 3-polytopes with cyclically 5-connected graphs[J]., 1974, 26(2): 138-146.

[9] BATAGELJ V. An inductive definition of the class of all triangulations with no vertex of degree smaller than 5[C]. Proceedings of the Fourth Yugoslav Seminar on Graph Theory, Novi Sad, 1983: 15-24.

[10] WAGNER K. Bemerkungen zum vierfarbenproblem[J].-, 1936, 46: 26-32.

[11] BRINKMANN G and MCKAY B D. Construction of planar triangulations with minimum degree 5[J]., 2005, 301: 147-163. doi: 10.1016/j.disc.2005.06. 019.

[12] MCKAY B D. Isomorph-free exhaustive generation[J]., 1998, 26(2): 306-324. doi: 10.1006/ jagm.1997.0898.

[13] AVIS D. Generating rooted triangulations without repetitions[J]., 1996, 16(6): 618-632.

[14] NAKANO S. Efficient generation of triconnected plane triangulations[J]., 2004, 27(2): 109-122.

[15] BRINKMANN G and MCKAY B. Fast generation of planar graphs[J]. MATCH, 2007, 58(58): 323-357.

[16] BRINKMANN G and MCKAY B D. The program plantri [OL]. http://cs.anu.edu.au/~bdm/plantri.

[17] NEGAMI S and NAKAMOTO A. Diagonal transformations of graphs on closed surfaces[J]..I.,,, 1994, 40(40): 71-96.

[18] KOMURO H. The diagonal flips of triangulations on the sphere[J]., 1997, 44(2): 115-122.

[19] MORI R, NAKAMOTO A, and OTA K. Diagonal flips in Hamiltonian triangulations on the sphere[J]., 2003, 19(3): 413-418. doi: 10.1007/s00373- 002-0508-6.

[20] GAO Z C, URRUTIA J, and WANG J Y. Diagonal flips in labeled planar triangulations[J]., 2004, 17(4): 647-656. doi: 10.1007/s003730170006.

[21] BOSE P, JANSENS D, VAN RENSSEN A,. Making triangulations 4-connected using flips[C]. Proceedings of the 23rd Canadian Conference on Computational Geometry, Toronto, 2014, 47(2): 187-197. doi: 10.1016/j.comgeo.2012. 10.012.

[22] 許進. 極大平面圖的結(jié)構(gòu)與著色理論(1): 色多項式遞推公式與四色猜想[J]. 電子與信息學(xué)報, 2016, 38(4): 763-779. doi: 10.11999/JEIT160072.

XU Jin. Theory on the structure and coloring of maximal planar graphs(1): recursion formula of chromatic polynomial and four-color conjecture[J].&, 2016, 38(4): 763-779. doi: 10.11999/ JEIT160072.

[23] BONDY J A and MURTY U S R. Graph Theory[M]. Springer, 2008: 5-46.

[24] XU Jin, LI Zepeng, and ZHU Enqiang. On purely tree- colorable planar graphs[J]., 2016, 116(8): 532-536. doi: 10.1016/j.ipl.2016.03.011.

XU Jin: Born in 1959, Professor. His main research includes graph theory and combinatorial optimization, biocomputing, social networks, and information security.

Accepted: 2016-04-21;

Online published: 2016-04-26

*Corrcsponding author: XU Jin jxu@pku.edu.cn

Foundation Items: The National 973 Program of China (2013CB 329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

CLC index: O157.5

Document code: A

10.11999/JEIT160224

2016-01-24;