XU Jin

?

Theory on Structure and Coloring of Maximal Planar Graphs(3)Purely Tree-colorable and Uniquely 4-colorable Maximal Planar Graph Conjectures

XU Jin*

(Key Laboratory of High Confidence Software Technologies, Peking University, Beijing 100871, China)(School of Electronics Engineering and Computer Science, Peking University, Beijing 100871, China)

A maximal planar graph is called the recursive maximal planar graph if it can be obtained fromby embedding a 3-degree vertex in some triangular face continuously. The uniquely 4-colorable maximal planar graph conjecture states that a planar graph is uniquely 4-colorable if and only if it is a recursive maximal planar graph. This conjecture, which has 43 years of history, is a very influential conjecture in graph coloring theory after the Four-Color Conjecture. In this paper, the structures and properties of dumbbell maximal planar graphs and recursive maximal planar graphs are studied, and an idea of proving the uniquely 4-colorable maximal planar graph conjecture is proposed based on the extending-contracting operation proposed in this series of article (2).

Uniquely 4-colorable maximal planar graph conjecture; Purely tree-colorable planar graph conjecture; Dumbbell maximal planar graphs; Recursive maximal planar graphs

1 Introduction

Graph theory originated from the K?NIGSBERG seven bridges problem studied by EULERIN 1736, and the electric network problem studied by KIRCHHOFF in 1847. In the last 70 years, graph theory was rapidly developed. To its reason, one is influenced by the development of the electronic computer; the other more important is the Four-Color Conjecture. Specifically, due to the Four-Color Conjecture, many areas of graph theory were created, such as topological graph theory, maximum independent set and maximum clique theory, vertex and edge covering theory, chromatic polynomial theory, Tutte-polynomial theory, factor theory and integer flow theory, especially the graph coloring theory and so on.

In the field of graph coloring, apart from the famous Four-Color Conjecture, researchers have proposed many conjectures, including the uniquely 4-colorable maximal planar graph conjecture discussed in this paper. This conjecture was proposed by GREENWELL and KRONK[1]in 1973, which is closely related to the Four-Color Conjecture, and has not been resolved yet.

The concept of uniquely colorable graphs was proposed by GLEASON and CARTWRIGHT[2], and CARTWRIGHT and HARARY[3]successively. CARTWRIGHT and HARARY obtained some sufficient conditions for determining whether a labeled graph is uniquely colorable or not. Since then, many researches have been done in this field. For example, HARARY,[4]studied the connectivity and the number of edges of uniquely-colorable graphs. Furthermore, many scholars studied on the problem that whether there exists a uniquely-colorable graph withoutfor. NE?ETIL[5,6]studied the properties of critical- uniquely colorable graphs and proved that there exist uniquely-colorable graphs without triangles. In 1974, GREENWELL and LOVáSZ[7]proved that there exist uniquely-colorable graphs without short odd cycles; and in 1975, MüLLER[8]solved the general case of this problem by the method of construction (also see Ref. [9]), that is, for any integerand, there exists a uniquely- colorable graph with girth greater than. MüLLER[8,9], AKSIONOV[10], MELNIKOV and STEINBERG[11]investigated the edge-critical uniquely colorable graphs; WANG and ARTZY[12]showed that for, if there exists a uniquely-colorable graph without, then the number of edges of the graph is greater than; OSTERWEIL[13]constructed a kind of uniquely 3-colorable graphs by the so-called 6-cliquerings. Moreover, he demonstrated how to use this technique to construct uniquely-colorable graphs; BOLLOBáS and SAUER[14]proved that for alland, there exists a uniquely- colorable graph with girth at least. Also, they proved that for anyand, there always exists a critical-uniquely-colorable graph with at leastvertices; DMITRIEV[15]generalized the result of BOLLOBáS[16]; XU[17]proved that ifis a uniquely-colorable graph with orderand size, then, and showed this bound is the best possible. Furthermore, he conjecture that ifis a uniquely-colorable graph with orderand size, thencontains. At the same time, CHAO and CHEN[18]showed that for any integer, there exists a uniquely 3-colorable graph of orderwithout triangles; AKBARI,[19]proved that there exists a-free uniquely 3-colorable graphwith 24 vertices andedges, whereThis result disproved XU's conjecture[17].

In terms of the uniquely edge-colorable graphs, GREENWELL and KRONK[1]studied this problem first in 1973. They proposed a conjecture as follows.

In 1975, FIORINI[20]independently studied the problem of uniquely edge-colorable graphs, and obtained some similar results as GREENWELL and KRONK[1]. After that, many scholars involved in this field, such as THOMASON[21,22], FIORINI and WILSON[23], ZHANG[24], GOLDWASSER and ZHANG[25,26], and KRIESSELL[27].

In 1977, FIORINI and WILSON[23], and FISK[28]independently proposed the following conjecture, respectively.

Conjecture 2 Any uniquely 3-edge-colorable cubic planar graph with at least 4 vertices contains a triangle.

This conjecture was proposed based on Conjecture 1. FOWLER[29]also investigated this conjecture in detail. However, it is still open.

As for uniquely colorable planar graphs, CHARTRAND and GELLER[30]completed many important works in 1969. They proved that any uniquely 3-colorable planar graph of ordercontains at least two triangles, any uniquely 4-colorable planar graph is a maximal planar graph, and there is no uniquely 5-colorable planar graph.

What is the necessary and sufficient condition for a planar graph to be uniquely 3-colorable? This problem is still open. Many scholars studied the properties of uniquely 3-colorable planar graphs. In 1977, AKSIONOV[31]proved that uniquely 3- colorable planar graphs with ordercontain at least 3 triangles, also described the structure of those graphs contain exactly 3 triangles. In the same year, MELNIKOV and STEINBERG[11]investigated the edge-critical uniquely 3-colorable planar graphs and proposed the following problem: find the exact upper boundof edges in edge-critical uniquely 3-colorable planar graphs with order. In 2013, MATSUMOTO[32]provedRecently, LI,[33,34]proved, and showed that there exist adjacent triangles in uniquely 3-colorable planar graphs containing at most 4 triangles.

Naturally, a problem will be raised that which maximal planar graphs are uniquely 4-colorable? In other words, what is the characteristic of uniquely 4-colorable planar graphs? Obviously, this problem is the key to study uniquely 4-colorable planar graphs. So far, many scholars have been investigating this problem.

Indeed, FISK[28]proposed a conjecture equivalent to Conjecture 2.

Conjecture 3 A planar graphis uniquely 4-colorable if and only ifis a recursive maximal planar graph.

It can be checked that Conjecture 2 and Conjecture 3 are equivalent, and both of them are the special case of Conjecture 1. In 1998, BOHME,[35]proved that the minimum counterexample of this conjecture is 5-connected. We call Conjecture 3 the uniquely 4-colorable maximal planar graph conjecture.

All graphs considered in this paper are finite, simple, and undirected. For a given graphand a vertexofanddenote the vertex set, the edge set, the degree of, and the neighborhood of(the set of all vertices adjacent to) respectively, which are written as,,, andfor short. The cardinalityof the setis called the order of. For a graph, if,, thenis called a subgraph of. Wheneverare adjacent in the graph, they are also adjacent in the graph, thenis called an induced subgraph of. An induced subgraph ofwith vertex setis denoted by. By starting with a disjoint union ofandand joining every vertex ofto every vertex ofby adding edges, one obtains the join ofand, denoted by. We useto denote the complete graph of order. The joinof a cycle and a single vertex is referred to as a wheel withspokes, denoted by, whereandare called the cycle and the center of the wheel, respectively. If, we also write the cycleof the wheelas.

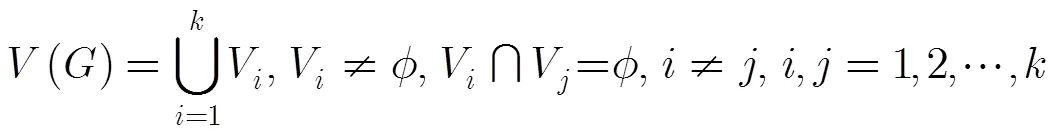
Similarly, the concept of edge coloring of a graph can be given, that is, an assignment from the color set to its edge set such that no two adjacent edges have the same color. A graphis uniquely-edge colorable if there is exactly one partition of the edge setintomatchings.

A maximal planar graph is a planar graph to which no new edges can be added without violating the planarity. A triangulation is a planar graph in which every face is bounded by three edges (including its infinite face). It can be proved that a maximal planar graph is equivalent to a triangulation.

The concepts and symbols not given in this paper can be viewed in Refs. [38,39].

2 Tree-colorings and Cycle-colorings

3 Purely Tree-colorable Maximal Planar Graphs

In Section 2, we partitioned maximal planar graphs into three classes: purely tree-colorable graphs, purely cycle-colorable graphs, and impure colorable graphs. It is difficult to give a necessary and sufficient condition to determine which class a maximal planar graph belongs to, even to describe the structure of these three kinds of maximal planar graphs. In fact, if we can characterize the purely tree-colorable graphs, then the uniquely 4-colorable maximal planar graph conjecture is proved naturally. So, we will study these three kinds of maximal planar graphs in the following series of papers, and mainly consider the purely tree-colorable graphs in this section.

3.1 Purely tree-colorable maximal planar graph Conjecture with minimum degree 5

In Ref. [41], it has been found that the icosahedron is a purely tree-colorable maximal planar graph with minimum degree 5, which has ten different tree-colorings shown in Fig. 2.

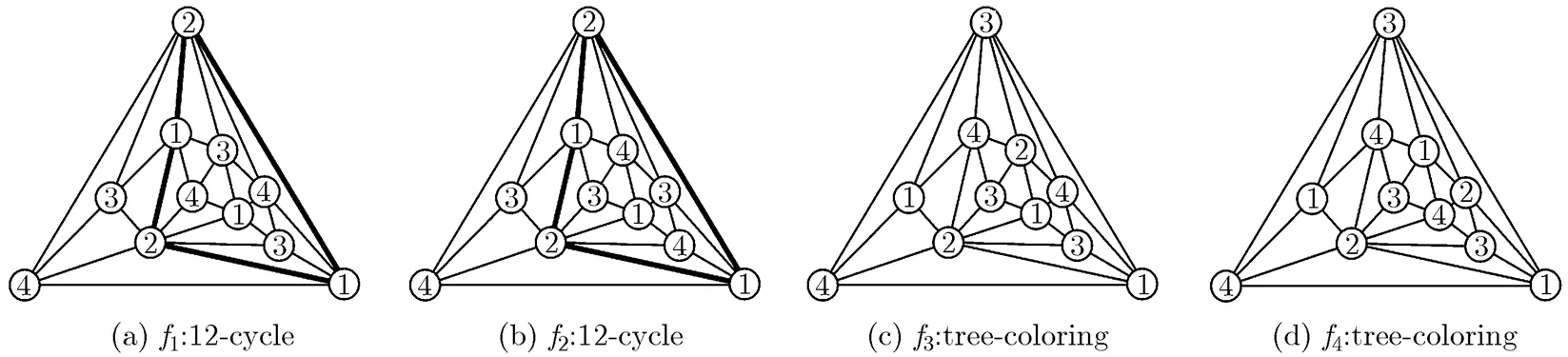
Fig. 1 All 4-colorings of a maximal planar graph with order 11

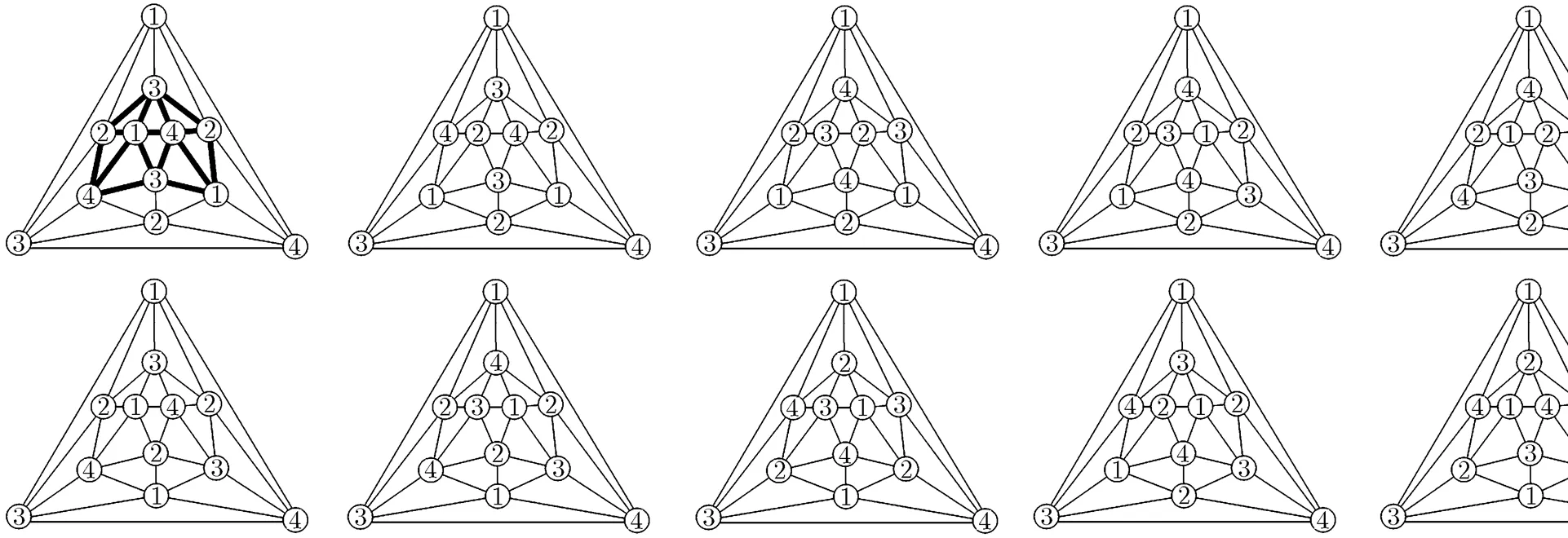
Fig. 2 The icosahedron and its all ten 4-colorings

Therefore, the domino configuration contained in the icosahedron with 2 inner vertices must be unique. We can choose the bold domino configuration of the first graph in Fig.2 as a representative.

3.2 Dumbbell-maximal planar graphs

3.2.1 Dumbbell transformation

The object graph of dumbbell transformation is a closed dumbbell, namely a 4-wheel, shown in Fig. 3. The so called dumbbell transformation is to replace the closed dumbbell by the fourth graph shown in Fig. 3(a) or Fig. 3(b). The specific steps are as follows:

Step 1 Split the wheel centerinto two verticesand, vertically or horizontally, shown in the second graph of Fig. 3(a) or Fig. 3(b), respectively.

Step 2 Extend to the third graph of Fig. 3(a) or Fig. 3(b).

Step 3 Add a 2-length path in the 6-cycle, vertically or horizontally, and then join edges between the 2-length path and 6-cycle to form the configuration shown in the fourth graph of Fig. 3(a) or Fig. 3(b).

Moreover, the inverse operation of dumbbell transformation is called dumbbell contracting- transformation, and the fourth graph in Fig. 3(a) is called the object graph of dumbbell contracting- transformation. In Fact, the dumbbell transformation is equivalent to the extending 334- wheel operation, as shown in Fig. 3(c). For more information, readers can refer to this series of article (2) (see Ref. [39]).

3.2.2 Structure of dumbbell-maximal planar graphs

In the following, we give the steps to construct a dumbbell-maximal planar graph of orderfrom.

Step 1 Find all unidentical closed dumbbells

Fig. 3 The object graph and the process of dumbbell transformation

Step 2 Implement the dumbbell transformation on each unidentical 4-wheel in, then we can obtain dumbbell-maximal planar graphs with order. For example,(shown in Fig. 4(b)) is obtained by implementing the dumbbell transformation on the 4-wheel bolded in(shown in Fig. 4(a)). It is easy to prove that there are two closed dumbbells inwhich are identical. So, we obtain two dumbbell-maximal planar graphs with order 17 by implementing the dumbbell transformation, shown in Fig. 4(c) and Fig. 4(d), respectively.

3.2.3 Properties of dumbbell-maximal planar graphs

We further discuss some properties of dumbbell maximal planar graphs in this subsection.

Theorem 1 (1) Any dumbbell-maximal planar graph contains exactly 3 vertices of degree 4; (2) Any dumbbell-maximal planar graph hasvertices, where; (3) Every dumbbell- maximal planar graph is purely tree-colorable, and each dumbbell maximal planar graph with orderhas exactlydifferent colorings.

(3) By induction. Obviously, the result holds ifThe dumbbell-maximal planar graph of order 13 has totally 4 different colorings and each of these colorings is tree-coloring, shown in Fig. 5. So, the theorem holds.

Suppose that the result holds for, that is,is purely tree-colorable and has exactlydifferent colorings. Now, we discuss the case of. Letbe a 4-wheel ofandbe the center of the wheel, shown in Figs. 6(b). Implement the dumbbell transformation on dumbbellof(shown in Figs. 6(a) and 6(c)). Suppose that the obtained graphcontains a bicolored cycle, then there must exist a, such thatcontains a bicolored cycle. So, there are two cases: one is, shown in Fig. 6(a); the other is, shown in Fig. 6(c). For both of the two cases, we can obtainby implementing the dumbbell contracting-transformation. Since the dumbbell contracting-transformation is indeed implementing contract 4-wheel operation one time and then contract 3-wheel two times, the natural coloring (based on) of the obtained graph contain bicolored cycles. This contradicts the fact thatis purely tree-colorable. So,

Fig. 4 Four dumbbell-maximal planar graphs with lower orders

Fig. 5 All 4-colorings of the dumbbell maximal planar graph with order 13

Fig. 6 Dumbbell transformation and dumbbell contracting-transformation based on colorings

is purely tree-colorable.

Without loss of generality, we suppose that each 4-wheel ofis colored as Fig. 6(b). Then subject to the coloring of the external cycle, the dumbbell contracting-transformation object subgraph ofhas exactly 2 colorings, as shown in Fig. 6(a) and Fig. 6(c), respectively. So,has exactlydifferent colorings. The proof is completed.

3.2.4 Enumeration

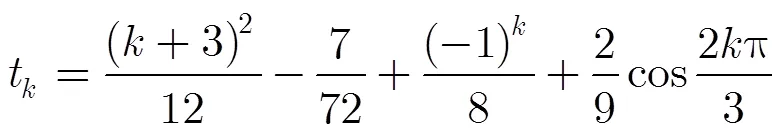
The proof can be found in Ref. [41].

4 Recursive Maximal Planar Graphs

In addition to the Four-Color Conjecture, the uniquely 4-colorable maximal planar graph conjecture (Conjecture 3) has been a very influential conjecture in the graph coloring theory, which has 43 years of history. Uniquely 4-colorable maximal planar graphs are conjected to

be recursive maximal planar graphs[28], so we study

on this class of graphs in this section.

The so called recursive maximal planar graph (RMPG) is obtained fromby embedding a 3-degree vertex in some triangular face continuously, where embedding a 3-degree vertex in a triangular is to add a vertex on the face of this triangular, and then connect this vertex to the three vertices of the triangular. In this paper,denotes the set consisting of all RMPGs andthe set of graphs inwith order. Let. Obviously,,, the corresponding RMPGs are shown in Fig. 7.

4.1 Basic properties

Proof By induction on the numberof vertices. When,, and the corresponding graphs are shown in Fig. 7. So the result is true obviously.

Assume that the theorem holds when. That is, for any RMPGwithvertices, it has at least two 3-degree vertices, and all the vertices of 3-degree are not adjacent to each other.

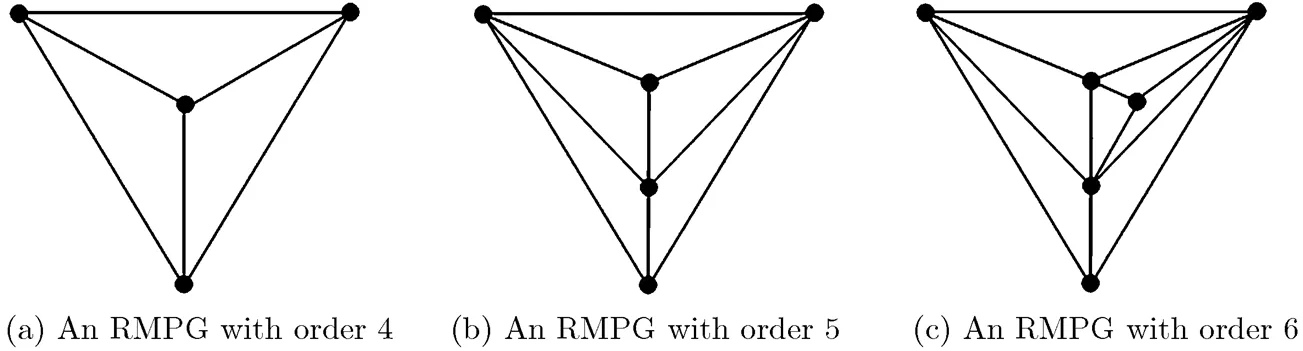
Fig. 7 Three RMPGs with orders 4,5,6

3-degree are not adjacent to each other in. For, if 3-degree vertices are included in, then one exists at most, saying. Obviously, there is at least another 3-degree vertex except forin, and all those 3-degree vertices are not adjacent to each other. Sinceis a 3-degree vertex ofand it is not adjacent to any other vertices except for, there are also at least two 3-degree vertices in, and all those 3-degree vertices are not adjacent to each other. Thus, the conclusion holds. For, if there exists no 3-degree vertices in, the conclusion holds by the same way above. The theorem follows by the principle of induction.

Theorem 4 (1) There exists no maximal planar graph having exactly two adjacent vertices of degree 3; (2) There exists no maximal planar graph with exactly three vertices of degree 3 adjacent to each other.

Proof (1) By contradiction. Assume thatis a maximal planar graph with two adjacent vertices, satisfying. Let. Notice thatis a maximal planar graph andmust be in a triangular face which consists of the vertices,, and. In other words,is adjacent toand. These four vertices can form a subgraph, as shown in Fig. 8. Sinceis a maximal planar graph, if there exist any other vertices of, then it can form a triangle withor. It contradicts. Otherwise, if there exists no other vertices, thenis isomorphism to, which has four vertices of degree 3. Therefore, there exists no maximal planar graph with two adjacent vertices of 3-degree exactly. Similarly, (2) holds.

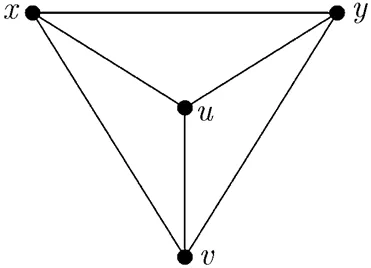
Fig. 8

(2)There exists only one 3-degree vertex;

(3)There exactly exist two 3-degree vertices;

(4)There exactly exist three 3-degree vertices.

For Case (1), the theorem holds naturally, and the Cases (3) and (4) do not exist by Theorem 4. So we just need to consider the Case (2). In this case, there exists only one 3-degree vertex in subgraph, denoted by. Let. Like the method mentioned above, if, then the theorem holds. Otherwise,must contain a 3-degree vertex. In this way, we can getwithin finitesteps. Otherwise,whencontains only four vertices. It means that the graphis an RMPG. But there is only one 3-degree vertex in, which contradicts Theorem 3.

4.2 (2,2)-recursive maximal planar graphs

In this subsection, we introduce and study (2,2)- RMPGs, which are a special class of RMPGs. An RMPG is called a (2,2)-RMPG if it contains only two vertices of degree 3, and the distance between them is 2. It is easy to check that there exists only one (2, 2)-RMPG with orders 5 and 6, shown in Fig. 9(a) and Fig. 9(b), respectively.

To understand the structure of (2,2)-RMPGs,

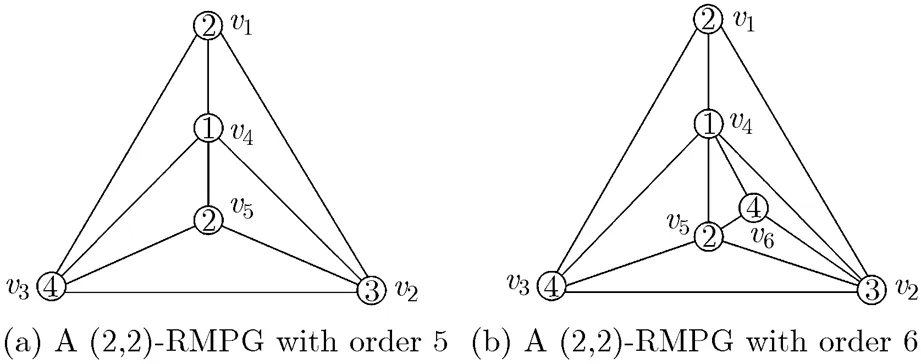
Fig. 9 (2,2)-RMPGs with orders 5 and 6

we divide three inner faces of the complete graphinto three regions, and label its vertices correspondingly. In Fig.10, the triangle labeled byis called the outside triangle, and the vertexis called the central vertex. Here we define that the verticesare colored with color 2, color 3, color 4, and color 1, respectively. The four vertices and their corresponding colorings are called the basic axes in the color-coordinate system of a (2,2)-RMPG. Four color axes are(color 1),(color 2),(color 3),(color 4). Obviously, there exists no (2,2)- RMPG with order 4; and there is only one (2,2)- RMPG with 5 vertices up to isomorphism, which can be obtained by embedding a 3-degree vertex in the region I, II or III of the graph(shown in Fig.10). Without loss of generality, we make an agreement that new vertices are only added in the region II. Thus, the vertex is colored by color 2 (Fig. 9(a)); the non-isomorphic (2,2)-RMPGs with order 6 can be obtained by embedding a 3-degree vertex in any region of the (2,2)-RMPG with order 5. It is easy to prove that this kind of graphs with 6 vertices obtained by embedding a new vertex in any face are isomorphic. Thus, there is only one (2,2)- RMPGs with order 6. In general, we make an agreement that the 6th vertex is embedded in the face composed of the vertices(.. the sub-region I of the region II), which is colored by color 4 (Fig. 9(b)). Further, for (2,2)-RMPGs with

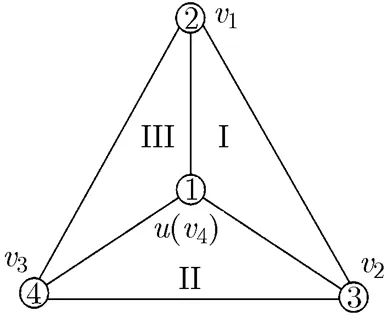
Fig. 10 The basic frame diagram of the color-coordinate system

higher orders, we restrict that new vertices are only added in the regions I and II, but not in the region III.

Based on the agreement above, we can discuss the classification of (2,2)-RMPGs. Two methods for this purpose will be introduced as follows.

The first is based on the region where the 3-degree vertices are embedded: (1) (2,2)-RMPGs

which are obtained by successively embedding 3-degree vertices only in the region II, such graphs are shown in Fig.11; (2) (2,2)-RMPGs are obtained by successively and randomly embedding 3-degree vertices in the regions I and II, shown in Fig.12. For maximal planar graphs, we have a straightforward fact as follows.

Proposition 1 Any face in a maximal planar graph can become the infinite outside face.

That is, the (2,2)-RMPGs mentioned above are obtained by embedding 3-degree vertices randomly in the regions I and II. We can transform any 3-degree vertex in the regions I or II to the outside triangular face by Proposition 1, which is equivalent to the first classification. It means that this kind of (2,2)-RMPGs are obtained by successively embedding 3-degree vertices only in the region II. Therefore, we only consider this kind of graphs in the later sections.

The second method is based on whether there exists a common edge between the two triangular surfaces of two 3-degree vertices or not. It is called the adjacent type if there is a common edge;

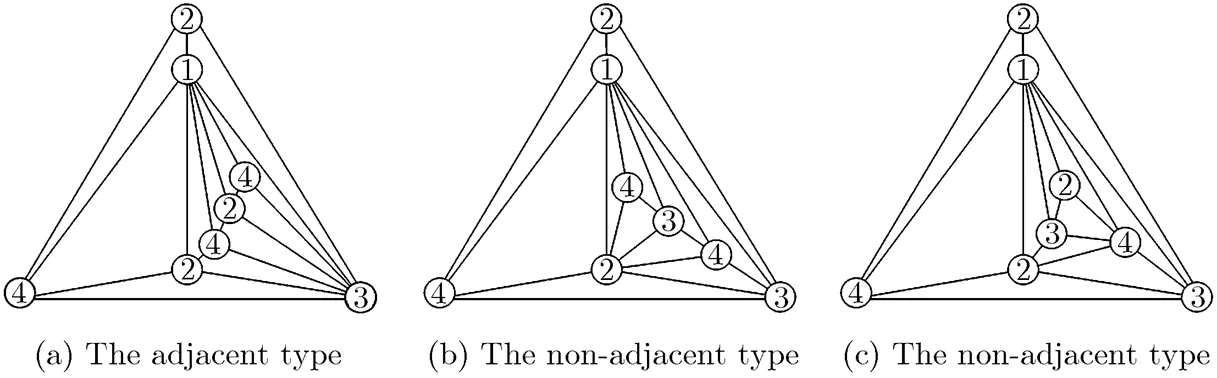
Fig. 11 The (2,2)-RMPGs obtained by embedding 3-degree vertices only in the region II

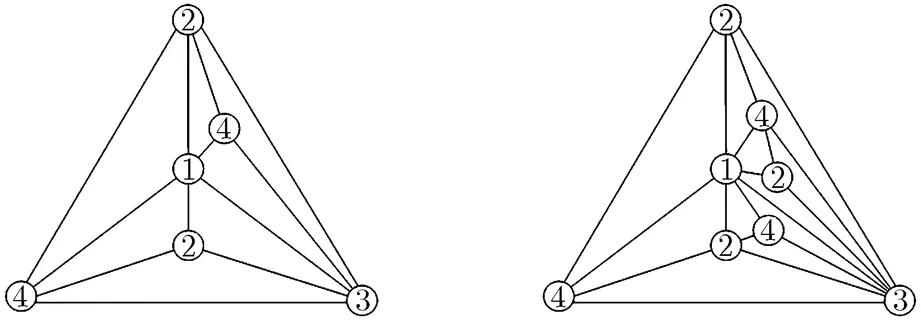
Fig. 12 The (2,2)-RMPGs obtained by embedding 3-degree

vertices in the regions I and II randomly

otherwise, the non-adjacent type. As shown in Fig. 11, the first graph belongs to the adjacent type, whereas the last two graphs belong to the non- adjacent type.

In Fig. 9(a), the (2, 2)-RMPG with order 5 is a double-center wheel, and the degree of vertices in the neighbor of each center is 4, where a double- center wheel is a specific maximal planar graph constructed by the join of a cycle and two single vertices. When the order of a (2,2)-RMPG is not less than 6, we have the following results.

Proof (1) By induction. There is only one maximal planar graph of order 5 (shown in Fig. 9(a)), it is also a double-center wheel, so all triangular faces are equivalent. Therefore, in the view of isomorphism, there exist only one RMPG with order 6, also a (2,2)-RMPG (shown in Fig. 9(b)). Thus, the theorem holds when.

Assume that the theorem holds when. We now consider a (2, 2)-RMPGof order. Suppose thatis a 3-degree vertex in, then there are two cases as follows:

Case 1 two or three vertices of 4-degree are included in, thenis also an RMPG with order at least 6 which contains two or three vertices with degree 3 adjacent to each other, which contradicts with Theorem 3.

Case 2 There exists no vertex of degree 4 in, thenis also an RMPG with order at least 6 which contains only one vertex of degree 3, which contradicts with Theorem 3.

In conclusion, we have proved that only one vertex of degree 4 is included in.

(2) and (3) can be proved by the gradual construction of (2,2)-RMPGs. The proof is completed.

ProofAny (2,2)-RMPG can be obtained by embedding 3-degree vertices in the region II from the (2,2)-RMPG with order 6. When embedding the-th vertex in (2,2)-RMPG with order,, there are only 2 triangles can be chosen for the non-adjacent type and 3 triangles for the adjacent type. It is easy to prove that the graphs obtained by embedding 3-degree vertices in the two faces incident with the 4-degree vertex are isomorphic. Therefore,The (2,2)- RMPGs with orders 7, 8, 9 are shown in Fig. 13, respectively. The proof is completed.

4.3 The colorings of extending 4-wheel operation graphs

Without loss of generality, we can always assume that the (2,2)-RMPGis obtained by embedding 3-degree vertices only in the region II in following discussion. Thus, a (2,2)-RMPGcan be uniquely represented by its color sequence.

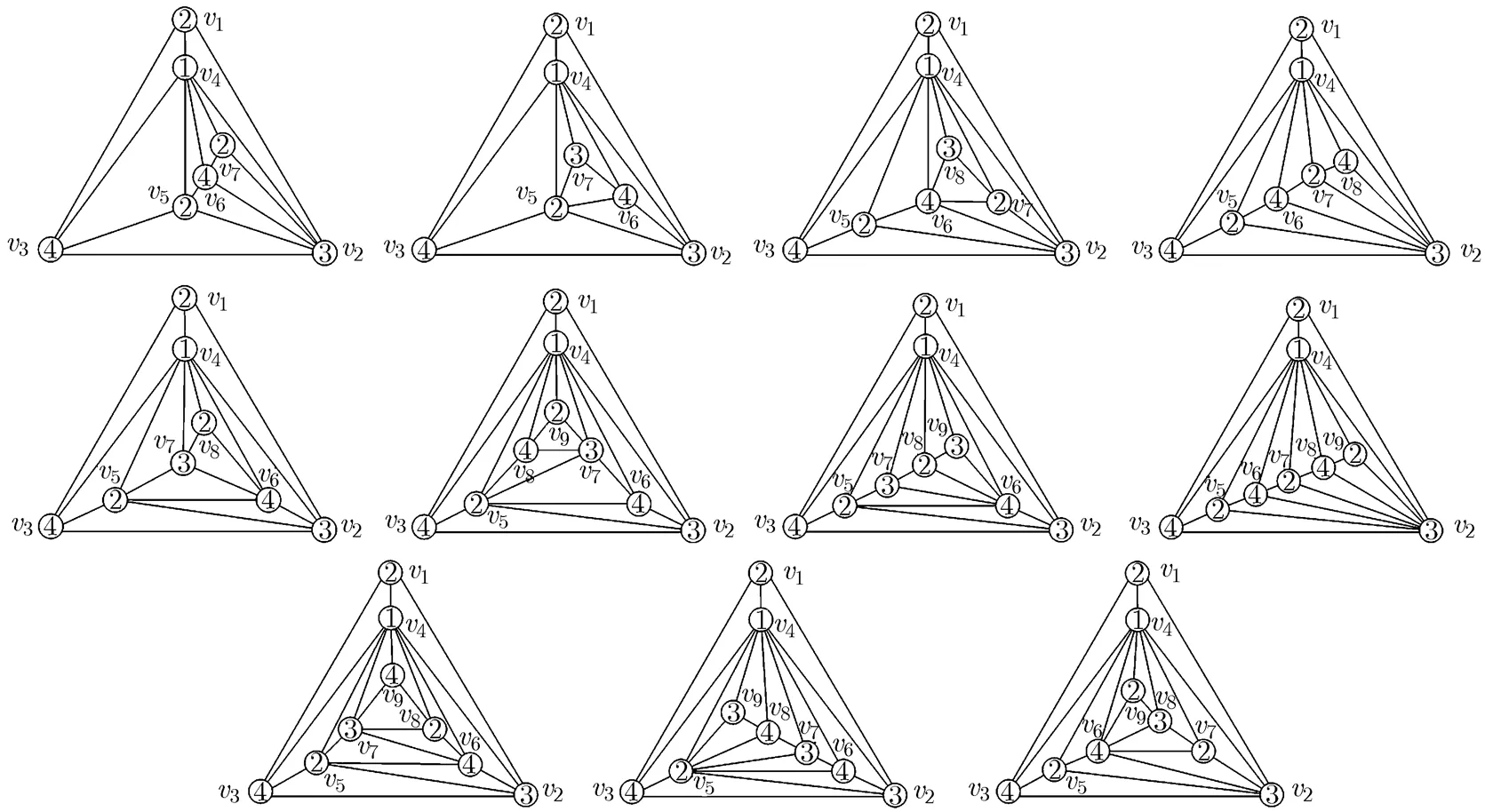
Fig. 13 All of the (2,2)-RMPGs with orders 7, 8, 9

According to the definition of (2,2)-RMPGs, this representation also determines the structure of a graph. This structure starts from(shown in Fig. 10), and selects a triangular face to embed vertices according to the color of each vertex.

For example, for the color sequence, its corresponding (2, 2)-RMPG is the middle graph of row 3 in Fig. 13.

For the color sequence of a (2,2)-RMPG, we can obtain the following:

Proof It follows from Fig. 10 that,,and. Then we obtainby Fig. 9(a) andby Fig. 9(b). Again by Fig. 9(b),or. The proof is completed.

In the following, we are devoted to discussing the vertex coloring problem of the induced graph from a (2,2)-RMPG by extending 4-wheel operation. We know that any given (2,2)-RMPG is uniquely 4-colorable, and every vertex can also be colored determinately.

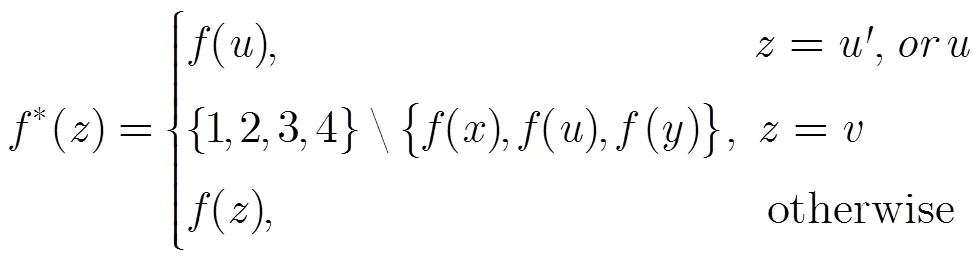
Naturally, one question is proposed that whether the graphobtained by extending 4-wheel operation is uniquely 4-colorable or not. In fact, the answer is negative, that is,.

Proof Obviously, the conclusion holds when. So we only need to consider the case when. Let,,,,. According to Theorem 7, only vertexincan be colored with coloring 1, so the vertexshould be colored with coloring 3 or 4. Without loss of generality, let. Sinceis a (2,2)-RMPG, it can be obtained fromby addingvertices of degree 3 in turn, namely. Letbe the vertex adjacent toand with the largest subscript in, thenor.

Remark In Theorem 10, we showed that the graphobtained from a (2,2)-RMPGby extending 4-wheel operation on the pathis not uniquely 4-colorable, wheremust be 3- degree vertices of. Whenare not vertices of degree 3, the graphmay be uniquely 4- colorable.

5 An Idea to Prove the Uniquely 4-colorable Maximal Planar Graph Conjecture

The uniquely 4-colorable maximal planar graph conjecture is still an open problem until now. The object of this conjecture is the RMPG, so we discussed the properties of RMPGs in detail. Also, we have proposed the purely tree-colorable maximal planar graph conjecture in Ref. [41], and if this conjecture holds, then the uniquely 4- colorable maximal planar graph conjecture is solved. Specially, we studied the dumbbell maximal planar graphs in Section 3 of this article. In this section, we give an idea to prove the uniquely 4-colorable maximal planar graph conjecture, which in fact is an idea to prove the purely tree-colorable maximal planar graph conjecture.

In the following, we give an idea to prove the purely tree-colorable maximal planar graph conjecture. Specifically, we need to prove the 9 cases below one by one.

For more information, we refer the reader to XU[39](Subsection 3.4, especially for the Fig. 17). In addition, studies on this conjecture will be given in the later article of this series.

6 Conclusion and Prospection

In this paper, we mainly studied a famous conjecture in graph coloring theory, the uniquely 4-colorable maximal planar graph conjecture. Since any uniquely 4-colorable maximal planar graph is conjected to be an RMPG, we studied the RMPGs in Section 4.

In Ref. [41], we proposed the purely tree- colorable graphs conjecture, which states that a maximal planar graph is purely tree-colorable if and only if it is the icosahedron or a dumbbell maximal planar graph. Moreover, we proved that if this conjecture holds, then the uniquely 4-colorable maximal planar graph conjecture also holds. So, we further studied the structures and properties of dumbbell maximal planar graphs in Section 3.

Finally, we give an idea to prove the purely tree- colorable graphs conjecture, which naturally implies the uniquely 4-colorable maximal planar graph conjecture. Specifically, suppose thatis purely tree-colorable, there are 9 cases to prove the conjecture based on the extending-contracting operation proposed in this series of article (2) and the result that any maximal planar graph with orderand minimum degreehas a father- graph or a grandfather-graph. Among the 9 cases, 8 cases are negative and only one is positive.

The work of this paper lays a foundation for proving the purely tree-colorable graphs conjecture. In the later article of this series, we will give the extending-contracting operational system of 4- colored maximal planar graphs, simply as the colored extending-contracting operational system. On this basis, the purely tree-colorable graphs conjecture is expected to be solved.

Acknowledgements The author would like to thank Professor YAO Bing, CHEN Xiang’en, WU Jianliang, and my students ZHOU Yangyang, LI Zepeng, LIU Xiaoqing, ZHU Enqiang, and WANG Hongyu for some useful discussions. Finally, the author would especially like to thank the Academician HE Xingui and Processor YU Daoheng of Peking University for their reviews, selfless supports, and encouragements to accomplish this work.

References

[1] GREENWELL D and KRONK H V. Uniquely line-colorable graphs[J]., 1973, 16(4): 525-529. doi: 10.4153/CMB-1973-086-2.

[2] GLEASON T C and CARTWRIGHT F D. A note on a matrix criterion for unique colorability of assigned graph[J]., 1967, 32(3): 291-296. doi: 10.1007/ BF02289592.

[3] CARTWRIGHT F D and HARARY F. On the coloring of signed graphs[J]., 1968, 23(4): 85-89.

[4] HARARY F, HEDETNIEMI S T, and ROBINSON R W. Uniquely colorable graphs[J]., 1969, 6(3): 264-270. doi: 10.1016/S0021-9800(69) 80086-4.

[5] NESTRIL J. On critical uniquely colorable graphs[J]., 1972, 23(1): 210-213. doi: 10.1007/ BF01304871.

[6] NESTRIL J. On uniquely colorable graphs without short cycles[J]. Casopis Pro Pěstování Matematiky, 1973, 98(2): 122-125.

[7] GREENWELL D and LOVASZ L. Applications of product coloring[J]., 1974, 25(3): 335-340. doi: 10.1007/BF01886093.

[8] MULLER V. On colorable critical and uniquely colorable critical graphs[J]., 1974: 385-386.

[9] MULLER V. On coloring of graphs without short cycles[J]., 1979, 26(2): 165-176. doi: 10.1016/ 0012-365X(79)90121-3.

[10] AKSIONOV V A. Chromatically connected vertices in planar graphs[J]., Russian, 1977, 31(31): 5-16.

[11] MELNIKOV L S and STEINBERG R. One counter example for two conjectures on three coloring[J]., 1977, 20(77): 203-206. doi: 10.1016/0012-365X (77)90059-0.

[12] WANG C C and ARTZY E. Note on the uniquely colorable graphs[J].,, 1973, 15(2): 204-206. doi: 10.1016/0095-8956(73)90022-1.

[13] OSTERWEIL L J. Some classes of uniquely 3-colorable graphs[J]., 1974, 8(1): 59-69. doi: 10. 1016/0012-365X(74)90110-1.

[14] BOLLOBAS B and SAUER N W. Uniquely colorable graphs with large girth[J]., 1976, 28(6): 1340-1344. doi: 10.4153/CJM-1976-133-5.

[15] DMITRIEV I G. Weakly cyclic graphs with integral chromatic spectra[J]., 1980, 34(34): 3-7.

[16] BOLLOBAS B. Uniquely colorable graphs[J].,, 1978, 25(1): 54-61. doi: 10. 1016/S0095-8956(78)80010-0.

[17] XU S J. The size of uniquely colorable graphs[J].,, 1990, 50(2): 319-320. doi: 10. 1016/0095-8956(90)90086-F.

[18] CHAO C and CHEN Z. On uniquely 3-colorable graphs[J]., 1993, 112(1): 21-27. doi: 10.1016/0012- 365X(93)90220-N.

[19] AKBARI S, MIRROKNI V S, and SADJAD B S.-free uniquely vertex colorable graphs with minimum possible edges[J].,, 2001, 82(2): 316-318. doi: 10.1006/jctb.2000.2028.

[20] FIORINI S. On the chromatic index of a graph, III: Uniquely edge-colorable graphs[J]., 1975, 26(3): 129-140.

[21] THOMASON A G. Hamiltonian cycles and uniquely edge colorable graphs[J]., 1978, 3: 259-268. doi: 10.1016/S0167-5060(08)70511-9.

[22] THOMASON A G. Cubic graphs with three Hamiltonian cycles are not always uniquely edge Colorable[J]., 1982, 6(2): 219-221. doi: 10.1002/jgt. 3190060218.

[23] FIORINI S and WILSON R J. Edge colouring of graphs[J]., 1977, 23(1): 237-239.

[24] ZHANG C Q. Hamiltonian weights and unique edge-3- colorings of cubic graphs[J]., 1995, 20(1): 91-99. doi: 10.1002/jgt.3190200110.

[25] GOLDWASSER J L and ZHANG C Q. On the minimal counterexamples to a conjecture about unique edge-3- coloring[J]., 1996, 113: 143-152.

[26] GOLDWASSER J L and ZHANG C Q. Uniquely edge- colorable graphs and Snarks[J]., 2000, 16(3): 257-267. doi: 10.1007/PL00007221.

[27] KRIESELL M. Contractible non-edges in 3-connected graphs [J].,, 1998, 74(2): 192-201. doi: 10.1006/jctb.1998.1842.

[28] FISK S. Geometric coloring theory[J]., 1977, 24(3): 298-340. doi: 10.1016/0001- 8708(77)90061-5.

[29] FOWLER T. Unique coloring of planar graphs[D]. [Ph.D. dissertation], Georgia Institute of Technology, 1998: 19-55.

[30] CHARTRAND G and GELLER D. On uniquely colorable planar graphs[J]., 1969, 6(3): 271-278. doi: 10.1016/S0021-9800(69)80087-6.

[31] AKSIONOV V A. On uniquely 3-colorable planar graphs[J]., 1977, 20(3): 209-216. doi: 10.1016/ 0012-365X(77)90061-9.

[32] MATSUMOTO N. The size of edge-critical uniquely 3-colorable planar graphs[J]., 2013, 20(4): 1823-1831.

[33] LI Z P, ZHU E Q, SHAO Z H,. Size of edge-critical uniquely 3-colorable planar graphs[J]., 2016, 339(4): 1242-1250. doi: 10.1016/j.disc.2015.11.009.

[34] LI Z P, ZHU E Q, SHAO Z H,. A note on uniquely 3-colorable planar graphs[J]., 2016: 1-8. doi: 10.1080/00207160. 2016.1167196.

[35] BOHME T, STIEBITZ M, VOIGT M,. On uniquely 4-colorable planar graphs[OL]. url=cite-seer.ist.psu.edu/ 110448.html. 1998.

[36] DAILEY D P. Uniqueness of colorability and colorability of planar 4-regular graphs are NP-complete[J]., 1980, 30(3): 289-293. doi: 10.1016/0012- 365X(80)90236-8

[37] XU J and WEI X S. Theorems of uniquely-colorable graphs[J].(), 1995, 23: 59-62.

[38] BONDY J A and MURTY U S R. Graph Theory[M]., 2008: 6-58.

[39] XU J. Theory on structure and coloring of maximal planar graphs(2): Domino configurations and extending-contracting operations[J].&, 2016, 38(6): 1271-1327. doi: 10.11999/ JEIT160224.

[40] ZHU E Q, LI Z P, SHAO Z H,. Acyclically 4-colorable triangulations[J]., 2016, 116(6): 401-408. doi: 10.1016/j.ipl.2015.12.005.

[41] XU J, LI Z P, and ZHU E Q. On purely tree- colorable planar graphs[J]., 2016, 116(8): 532-536. doi: 10.1016/j.ipl.2016.03.011.

XU Jin: Born in 1959, Professor. His main research includes graph theory and combinatorial optimization, biocomputing, social networks, and information security.

2016-05-05

*Corresponding author: XU Jin jxu@pku.edu.cn

Foundation Items: The National 973 Program of China (2013CB 329600), The National Natural Science Foundation of China (61372191, 61472012, 61472433, 61572046, 61502012, 61572492, 61572153, 61402437)

2016-04-22; Accepted: 2016-04-26; Online published:

10.11999/JEIT160409

CLC index: O157.5 Document code: A