LUO Jian-ping

School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 200235, China,

E-mail: jp_luo@163.com

LU Zhi-ming

Shanghai Key Laboratory of Mechanics in Energy Engineering and Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

QIU Xiang

School of Science, Shanghai Institute of Technology, Shanghai 200235, China

LI Dong-mei, LIU Yu-lu

Shanghai Institute of Technology, Shanghai 200235, China

(Received September 24, 2012, Revised October 8, 2012)

EFFECT OF SWEEP AND EJECTION EVENTS ON PARTICLE DISPERSION IN WALL BOUNDED TURBULENT FLOWS*

LUO Jian-ping

School of Mechanical Engineering, Shanghai Institute of Technology, Shanghai 200235, China,

E-mail: jp_luo@163.com

LU Zhi-ming

Shanghai Key Laboratory of Mechanics in Energy Engineering and Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

QIU Xiang

School of Science, Shanghai Institute of Technology, Shanghai 200235, China

LI Dong-mei, LIU Yu-lu

Shanghai Institute of Technology, Shanghai 200235, China

(Received September 24, 2012, Revised October 8, 2012)

This paper studies the sweep and ejection events in a channel flow with Reτ=80 by using Direct Numerical Simulation (DNS). The effects of ejection and sweep events on the transport of fluid particles are analyzed separately through a quadrant technique. By analyzing trajectories of the particles released at different wall-normal locations, it is found that the particles from the ejection events mainly move upward while the particles from the sweep events move downward of the flow during short and intermediate diffusion time durations. Numerical results show that the effects of the ejection and sweep events on the mean displacement and the mean square dispersion remain for a long time, one-order of magnitude larger than the streamwise Lagrangian integral scales.

sweep, ejection, dispersion, quadrant analysis, turbulent channel flow

Introduction

One of the most ubiquitous properties of turbulent flows is the enhancement of transport processes, such as those of mass, heat or momentum, and many engineering devices depend on the ability to control and predict those processes for their successful operations[1]. It is now recognized that the downdrafts (orthe sweeps) and the updrafts (or the ejections) are the typical constitutive motions of coherent structures near the wall. These events make the most of contributions to both the Reynolds stresses and the momentum transfer[2]. Hence, the properties of these two types of eddy motions were extensively studied[1-9]. Keshavarzi et al.[3]studied experimentally the burst events, and their effects on the sediment entrainment and the deposition over two types of ripples, and found that the downstream of the ripple burst events are dominant in Quadrants 1 and 3, wheareas the upstream of the ripple burst events are dominant in Quadrants 2 and 4. Further, they found that the sediment entrainment/deposition would occur upstream/ downstream of the ripple burst events. Ojha and Mazumder[4]investigated experimentally the shear stress generation in a flow over a series of two-dimensional dunes and found that the relative dominance of the sweep and eject events in the generation ofshear stress is in a spatially cyclic manner near the bed region. Mianaei and Keshavarzi[5,6]found that at the stoss side of ripples, quadrants (II) and (IV) were dominant over quadrants (I) and (III), wheareas the reverse is true in the lee side. Huang et al.[7]discussed the bubble effects on the sweep and ejection events as a function of the Reynolds number. They found that the bubble might suppress the ejection and sweep events in high Reynolds number flows. The ejection-sweep cycle over bare and forested gentle hills was examined by Poggi and Katul[8]experimentally. It is shown that the ejections dominate the momentum transfer for both surface-covers at the top of the inner layer. However, the sweeps dominate the momentum transfer within and near the canopy. Besides these experimental studies, there were also extensive numerical simulations of the burst phenomena[1,9]. In conclusion, there were many studies of ejection and sweep events on momentum and particle transportation, but very few about the contributions of sweep and ejection events to the particle dispersion behavior in wall turbulent flows.

In this paper, we investigate in details the transport of fluid particles for a channel flow with a Reynolds number Reτ=80using the Direct Numerical Simulation (DNS) approach. The effects of the ejection and sweep events on the transport of the particles are analyzed separately.

1. Numerical results and discussions

A DNS of a turbulent channel flow is carried out with 96×65×64 mesh points at a Reynolds number of Reτ=uτδ/ν=80, where uτ, δ and ν are, respectively, the friction velocity, the half width of the channel and the kinematic viscosity. The domain dimesions in the streamwise, wall-normal, and spanwise directions are 1 880×160×630 in units of wall thickness. The corresponding grid numbers in three directions are 96×65×64. The mass conservation equation and the Navier-Stokes (the momentum) equations of incompressible fluids are as follows

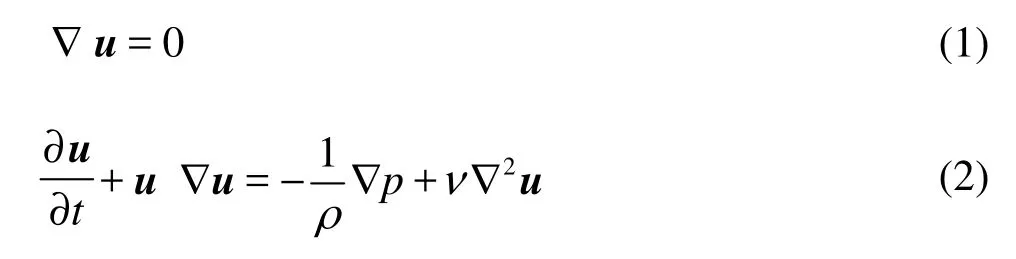
where u, ν and p are the velocity vector, the kinematic viscosity and the pressure, respectively. A pseudo-spectral method is used in the spatial domain to solve the Navier-Stokes equations. Orszag and Kells[10]proposed a method to split the Navier-Stokes equation in time with fractional steps to integrate the non-linear terms, the pressure and the viscous terms separately. Periodic boundary conditions are imposed on the streamwise and spanwise directions to obtain the velocity of the fluid particles. The velocity fields are computed and stored with a time intervalΔt+=/ν=0.2for a period of 1 000. The fluid particle velocity along a particle trajectory is computed by employing a third-order Hermite polynomials in the homogeneous directions and a Chebyshev polynomial in the wall-normal direction[11-13]. The particles are tracked through the computed velocity fields to obtain the Lagrangian velocity data[11-13].

The quadrant analysis is a useful technique to study how the turbulent fluctuations contribute to the momentum transfer throughout the bottom boundary layer[1,14,15]. As argued by Bogard and Tiederman[14], the quadrant analysis depends on the value of the hyperbolic-hole size H, and the optimum threshold for the buffer region is H≈1, based on direct comparisons between the detected events and instantaneous visualizations of the flow[14]. Following this line, we take H=1 in the present study[15].

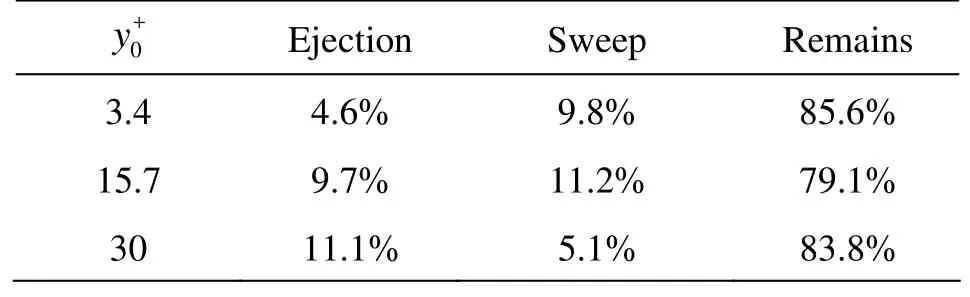
Table 1 Number-fraction of ejection and sweep particles at different released positions

Table 2 Lagrangian integral time scales in the streamwise ()and wall-normal () directions

Table 2 Lagrangian integral time scales in the streamwise ()and wall-normal () directions

+T+L 1 T2L3.4 30 6 15.7 42.7 10 30 48.5 12

Table 1 shows the number fraction of the ejection and sweep particles at various released positions (30 720 particles are released from each location). Note that only a small fraction of particles participate in the ejection and sweep events, as shown below, however, the ejection and sweep events play a dominant role in the particle dispersion behavior. It is also seen from Table 1 that more sweep events are detected than the eject events in a viscous sub-layer(y+=

0 3.4), whereas more eject events than sweep events are detected in a log-layer (y+=30). The Lagrangian in-

0 tegral time scale is an important typical time scale in the study of particle dispersion. The Lagrangian integral scales at three different vertical positions obtained by using the autocorrelation method are listed in Table 2. It is clearly seen that longitudinal integral timescales are much longer than the vertical ones.

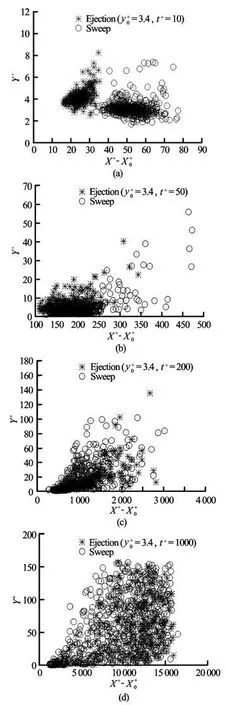
Fig.1 Distribution of particles released from y+=3.4 inx-0y plane at different times

Now we focus our attention to the different contributions of the eject and the sweep events in the boundary layer to the mean displacements in both streamwise and wall-normal directions. Figure 1 shows the evolution of the particle distribution released from= 30 in x-y plane at t+=10, 50, 200and1 000,respectively,wheredenotesthereleased position in the streamwise direction. In the figure, the notation “ejection” denotes the particles originally in the ejection events, and the notation“sweep” means the particles originally in the sweep events. It is clearly seen that the particles from the sweep or the ejection events move in different ways, particularly at the early stage, i.e., the particles from the ejection events mainly move upward (i.e., leave the wall) and streamwise at the same time, while the particles from the sweep events move downstream close to the wall. The different movements of the particles from the sweep and the ejection events can still be seen clearly at t+=200. Similar behavior is found for the particles released from=15 or 30, but they are not shown here for clearness of the picture. To see more clearly (quantitatively) the different movements of the particles from the sweep and the ejection events, we plot the difference of the mean displacementsof the ejected and the swept particles released from three different locations as shown in Fig.2. First, it is found that, for the three release locations, the mean displacements of the particles from the sweep eventsare larger than that from the ejection eventswhen t+is less than aboutandbecomes smallerthanwhen t+≥, wheredenotes the integral time scale in the streamwise direction as listed in Table 2. This behavior can be mainly explained as follows. During the early stage, the particles from the sweep events have a larger streamwise velocity and move faster than those from the ejection events, and after some time (about one to two integral time scales after releasing), the ejected particles gather a higher momentum from the surrounding fluid as they leave the wall whereas the swept particles lose their high momentum as they approach the wall. Secondly, the displacement difference between the ejected and the swept particles is much larger for the particles released from=3.4 as compared to the particles released from=15.7 and 30 in a large time duration. The un-vanished difference between the ejected and the swept particles may indicate that the particles from the sweep motion stay for a fairly long time in the low-speed area close to the wall.

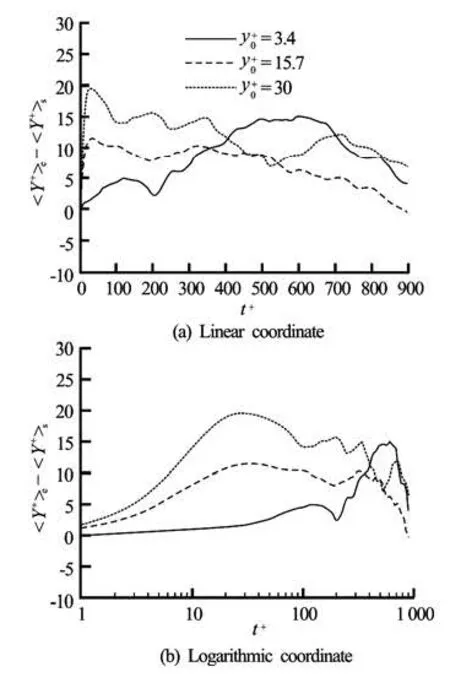
Fig.3 Difference of mean displacementbetween the ejected and the swept particles released from different locations

Figure 3 shows the difference of the mean displacement between the ejected and the swept particles released from y+=3.4, 15.7, 30 in the wall-normal

0direction. The difference between sweep and ejection is clearly seen in a short diffusion duration. First, The differenceincreases rapidly with time for a short duration and then decreases gradually with time when t+passes the pointfor the particles released from=15.7 and 30. Meanwhile, for the particles released from=3.4, the differenceincreases slowly with time at the early stage, then rapidly after t+≈200, reaches the maximum value at about the time t+≈500, and after that, the difference decreases steadily. Secondly, the difference for the case t+<300 increases with the initial releasing distance from the wall. i.e.,

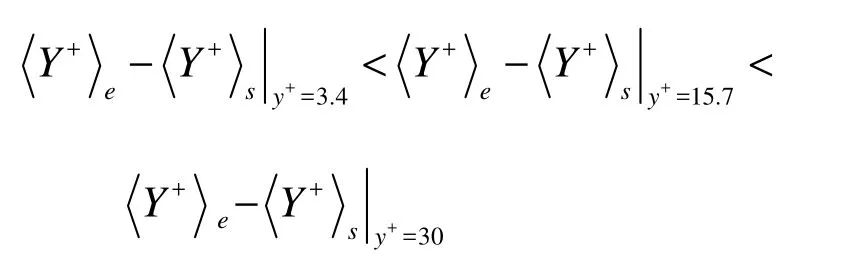
when t+<300. For a large diffusion time duration, the particles are expected to distribute uniformly across the whole channel, so little difference is generated by ejection and sweep, i.e., the differencedecreases for a long time and disappears in a sufficiently long time. This property is demonstrated in Fig.3.

Now, we consider the particle’s mean-square dispersion, which is calculated as

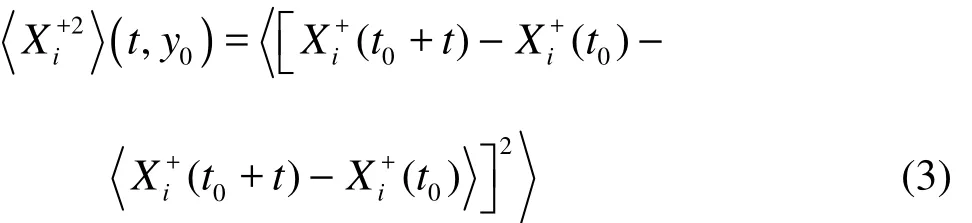
where y0and t0are the initial spatial location and the initial time. The different behaviors of the meansquare dispersion in three directions for the particles released from the viscous sub-layer, the buffer layer and thelog layer were investigated in detail byLuoet al.[10]. In this study, we consider especially theeffects of the sweep and eject events on the mean-square dispersion. The mean-square dispersionin the streamwise and wall-normal directions for the particles released from the viscous sublayer (=3.4), the buffer layer (=15.7) and the log layer(= 30)are shown in Figs.4-5. For a comparison, the results for the dispersion of all released particles are also shown in these figures. As explained in Ref.[10], the results offor all particles show that the particles released from each layer disperse in proportion to t+2for short diffusion time durations, to t+3for intermediately large time durations due to the mean shear, and to t+1for a long time duration. It is interesting to note that the dispersion behavior for eitherthe ejection or the sweep events is qualitatively the same as the total dispersion behavior, i.e., there also exist three regimes with different power indices after the release of the particles. Quantitatively, the particle dispersion for the sweep events at a short time duration is smaller than that for the ejection events when the particles are released from the viscous sublayer (=3.4), but the reverse is true if the particles are released from the log layer (=30). Meanwhile, it is seen that the dispersion for the two events is nearly the same when the particles are released from the buffer layer (=15.7). This means that the sweep events disperse the particles in the streamwise direction more efficiently than the ejection events in the viscous sublayer and the reverse is true in the log layer. While the efficiency of the sweep and the ejection events is approximately the same near the buffer layer.

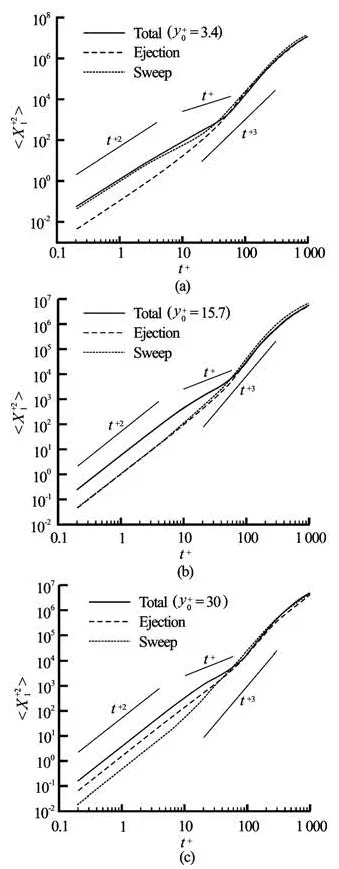
Fig.4 Mean-square dispersion of particles released from= 3.4, 15.7, 30 in the streamwise direction

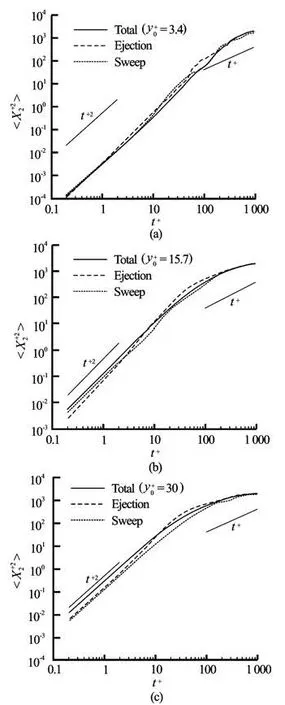
Fig.5 Mean-square dispersion of particles released from= 3.4, 15.7, 30 in the wall-normal direction

From Fig.5, it is seen that the dispersion in the wall normal direction from both events is proportional to t+2for a short time duration, then reduces tot+1for an intermediate time duration and finally reduces to t+0due to the wall constraint. The difference of the mean square dispersion between the two coherent events is relatively small except during the period of several integral time scales. The non trivial difference between the two coherent events in both streamwise and wall normal directions during an intermediate time duration needs a further investigation.

2. Conclusions

In this paper, the DNS method is applied to study the contributions of the sweep and ejection events to the particle dispersion in the wall-bounded turbulentflows with Reτ=80. The quadrant technique is adopted to analyze the events of sweep and ejection. By analyzing the trajectories of the particles released from the sweep and ejection events at different heights, it is found that remarkable differences appear for the mean displacement and the dispersion of the particles during short and intermediate diffusion time durations. The main results are as follows:

(1) The mean displacement of the particles released from the sweep events in the streamwise direction is larger than that from the ejection events at t+＜, but the reverse is true later on. The displacement difference between the ejected and thwswept particles is much larger for the particles released from=3.4as compared to the particles released from=15.7 and 30 after a long time. The initial effects of the ejection and sweep events on the mean displacement remain for several Lagrangian time scales.

(2) The mean square dispersion of the particles from the ejection and sweep events in the streamwise direction is proportional to t+2, t+3and t+1in the early time stage, the intermediate time stage and the long time stage, respectively for all three release locations. However, quantitatively, the dispersion of the particles from the sweep events is smaller (larger) than that from the ejection events when the particles are released from the viscous sublayer (the log layer), and the two dispersions are nearly the same when the particles are released from the buffer layer. Again, the numerical results show that the initial effects from the two events remain for quite a long time, as long as one-order of magnitude larger than the Lagrangian time scales.

[1] ADRIAN L. D., OSCAR F. and JAVIER J. Three-dimensional structure of momentum transfer in turbulent channels[J]. Journal of Fluid Mechanics, 2012, 694: 100-130.

[2] GUO H., BORODULIN V. I. and KACHANOV Y. S. et al. Nature of sweep and ejection events in transitional and turbulent boundary layers[J]. Journal of turbulence, 2010, 11(34): 1-51.

[3] KESHAVARZI A., BALL J. and NABAVI H. Frequency pattern of turbulent flow and sediment entrainment over ripples using image processing[J]. Hydrology and Earth System Sciences, 2012, 16(1): 147-156.

[4] OJHA S. P., MAZUMDER B. S. Turbulence characteristics of flow region over a series of 2-D dune shaped structures[J]. Advances In Water Resources, 2008, 31(3): 561-576.

[5] MIANAEI S. J., KESHAVARZI A. Spatio-temporal variation of transition probability of bursting events over the ripples at the bed of open channel[J]. Stochastic Environmental Research and Risk Assessment, 2008, 22(2): 257-264.

[6] MIANAEI S. J., KESHAVARZI A. Study of near bed stochastic turbulence and sediment entrainment over the ripples at the bed of open channel using image processing technique[J]. Stochastic Environmental Research and Risk Assessment, 2010, 24(5): 591-598.

[7] HUANG Jian, MURAI Yuichi and YAMAMOTO Fujio. Quadrant analysis of bubble induced velocity fluctuations in a transitional boundary layer[J]. Journal of

[8] POGGI D., KATUL G. The ejection-sweep cycle over bare and forested gentle hills: A laboratory experiment[J]. Boundary-Layer Meteorology, 2007, 122(3): 493-515.

[9] JIMENEZ J., HOYAS S. and SIMENS M. P. et al. Turbulent boundary layers and channels at moderate Reynolds numbers[J]. Journal of Fluid Mechanics, 2010, 657: 335-360.

[10] ORSZAG S. A., KELLS L. C. Transition to turbulence in plane posiseuille and plane coquette flow[J]. Journal of Fluid Mechanics, 1980, 96: 159-205.

[11] LUO J., USHIJIMA T. and KITOH O. et al. Lagrangian dispersion in turbulent channel flow and its relationship to Eulerian statistics[J]. International Journal of Heat and Fluid Flow, 2007, 28(5): 871-881.

[12] LUO Jian-Ping, LU Zhi-Ming and USHIJIMA T. et al. Lagrangian structure function’s exponents in turbulent channel flow[J]. Chinese Physics Letters, 2010, 27(2): 024708. Hydrodynamics, 2009, 21(1): 93-99.

[13] LUO Jian-ping, QIU Xiang and LI Dong-mei et al. High order Lagrangian velocity statistics in a turbulent channel flow with =Reτ80[J]. Journal of Hydrodynamics, 2012, 24(2): 287-291.

[14] BOGARD D. G., TIEDERMAN W. G. Burst detection with single-point velocity measurements[J]. Journal of Fluid Mechanics, 1986, 162: 389-413.

[15] LUO J., USHIJIMA T. and KITOH O. et al. Contributions of sweep and ejection events to particle disperrsion in wall turbulent flows[J]. Procedding of the 5th International Conference on Asian and Pacific Coasts. Singapore, 2009, 4: 93-99.

10.1016/S1001-6058(11)60305-3

* Project supported by the National Natural Science Foundation of China (Grant Nos. 11172179, 11102114), the Scientific Research Foundation for the Returned Overseas Chinese Scholars, State Education Ministry (Grant No. ZX2010-12), the Key Project of Shanghai Municipal Education Commission (Grant No. 11ZZ87) and the Shanghai Pujiang Program (Grant No. 08PJ1409100).

Biography: LUO Jian-ping (1964-), Female, Ph. D.,

Associate Professor

LU Zhi-ming,

E-mail: zmlu@staff.shu.edu.cn