郭育紅

(河西學(xué)院數(shù)學(xué)系,甘肅 張掖 734000)

關(guān)于正整數(shù)有序分拆的一些恒等式和n-colour有序分拆的兩個(gè)組合性質(zhì)

郭育紅

(河西學(xué)院數(shù)學(xué)系,甘肅 張掖 734000)

研究了正整數(shù)的無序分拆與有序分拆的關(guān)系.給出了正整數(shù)的無序分拆與有序分拆的一些恒等式.并且利用菲波拉契數(shù)與正整數(shù)n分拆成不含分部量1的有序分拆數(shù)的關(guān)系給出了n-colour有序分拆的兩個(gè)組合性質(zhì).

分拆恒等式;n-colour有序分拆;組合性質(zhì);菲波拉契數(shù)

1 引言

關(guān)于正整數(shù)無序分拆的第一個(gè)恒等式是由Euler[1]給出的.即:“將正整數(shù)分拆成分部量為奇數(shù)的分拆數(shù)等于將正整數(shù)分拆成互不相同的分部量的分拆數(shù)”.分拆恒等式一直吸引著數(shù)學(xué)工作者,同時(shí)也產(chǎn)生了許多豐富的結(jié)果[2-3].如著名的Rogers-Ramanujan恒等式曾是分拆理論中非常重要而有趣的一部分內(nèi)容.

然而,在分拆恒等式的研究中,對(duì)于與正整數(shù)的無序分拆和有序分拆相關(guān)的恒等式討論的卻相對(duì)比較少.2003年,文獻(xiàn)[4]發(fā)現(xiàn)了與正整數(shù)的無序分拆和有序分拆相關(guān)的一個(gè)恒等式,并且分別用分析和組合方法給出了證明.文獻(xiàn)[5-7]的作者相繼討論了一些與正整數(shù)的無序分拆和有序分拆相關(guān)的恒等式.本文第二節(jié)在文獻(xiàn)[5]的基礎(chǔ)上利用Agarwal的組合方法又給出了一些關(guān)于正整數(shù)有序分拆的恒等式.在第三節(jié),利用菲波拉契數(shù)與正整數(shù)的n-colour有序分拆的關(guān)系又得到了正整數(shù)的n-colour有序分拆的兩個(gè)組合性質(zhì).

首先,給出幾個(gè)定義:

定義 1.1[8]一個(gè)2行非負(fù)整數(shù)矩陣:

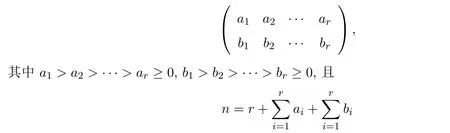
叫做正整數(shù)n的Frobenius-分拆.

正整數(shù)的任意一個(gè)無序分拆都能表示成Frobenius-分拆.事實(shí)上,在無序分拆的Ferrers圖中,假設(shè)主對(duì)角線上有r個(gè)點(diǎn).將這r個(gè)點(diǎn)刪掉,然后將主對(duì)角線右上方的點(diǎn)分別按各行計(jì)算,并將各行的點(diǎn)數(shù)仍以Ferrers圖中行排列的順序排成矩陣的第一行;同樣將主對(duì)角線下方的點(diǎn)分別按各列計(jì)數(shù),將各列的點(diǎn)數(shù)仍以Ferrers圖中列排列的順序排成矩陣的第二行,如果在Ferrers圖中第r行(列)沒有點(diǎn)就用“0”計(jì).于是就得到與該無序分拆對(duì)應(yīng)的Frobenius-分拆.

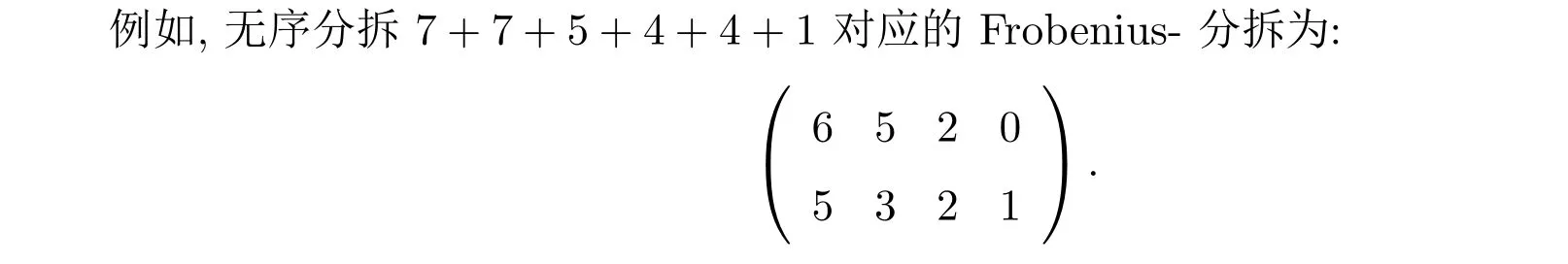
定義 1.2[4]正整數(shù)n的“奇-偶”無序分拆是指在n的無序分拆中分部量分別以奇數(shù)和偶數(shù)交替出現(xiàn),且最小分部量是奇數(shù)的無序分拆.

定義 1.3[5]正整數(shù)n的一個(gè)“奇”無序分拆是指其分部量為互不相同的奇數(shù)的無序分拆.

定義 1.4[5]正整數(shù)n的一個(gè)“偶”無序分拆是指其分部量為互不相同的偶數(shù)的無序分拆.

定義 1.5[4]一個(gè)k-彎是指在第一行和第一列各有k個(gè)點(diǎn)的向右彎曲的圖.

例如,下圖就是一個(gè)3-彎:

在文獻(xiàn)[4-5]中已經(jīng)證明了下述定理:

定理 1.1[4]將正整數(shù)n分拆成分部量為奇數(shù)的有序分拆數(shù)等于將正整數(shù)分拆成最大分部量為n的“奇-偶”無序分拆數(shù).

定理 1.2[5]將偶數(shù)n分拆成分部量為偶數(shù)的有序分拆數(shù)等于將正整數(shù)分拆成最大分部量為n的“偶”無序分拆數(shù).

注 本文中未加說明的概念或符號(hào)的含義與文獻(xiàn)[2]中的相同.

2 關(guān)于正整數(shù)有序分拆的恒等式

給出下面的定理:

定理 2.3 正整數(shù)n的有序分拆數(shù)等于最大分部量為2n?1的“奇”無序分拆數(shù).

證明 將定理 2.2中最大分部量為 n且滿足 Frobenius-分拆的自共軛無序分拆對(duì)應(yīng)的Ferrers圖中的每一個(gè)k-彎拉直就得到最大分部量為2n?1的“奇”無序分拆數(shù).

例 4 取n=4,則最大分部量為7的“奇”無序分拆有:

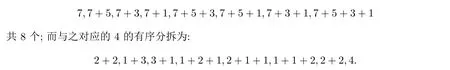
3 n-colour有序分拆的兩個(gè)組合性質(zhì)

文獻(xiàn)[9-10]拓廣了正整數(shù)無序分拆的概念,給出了正整數(shù)的n-colour無序分拆.即在正整數(shù)ν的無序分拆中對(duì)于每一個(gè)分部量n著n種不同的顏色.他們將這n種不同的顏色用下標(biāo)表示為:n1,n2,…,nn.類似正整數(shù)的有序分拆,文獻(xiàn)[11]又定義了n-colour有序分拆.即在n-colour無序分拆中考慮了分部量的順序.例如,3有8個(gè)n-colour有序分拆:

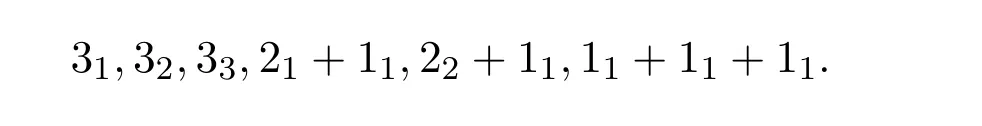
關(guān)于n-colour有序分拆的許多性質(zhì)見文獻(xiàn)[10-11].文獻(xiàn)[11]給出了下述結(jié)果:

引理 3.1[11]設(shè)C(m,ν)和C(ν)分別表示正整數(shù)ν分成m個(gè)分部量的n-colour有序分拆數(shù)和ν的所有n-colour有序分拆數(shù);c(m,q)和c(q)分別表示c(m,ν)和c(ν)的生成函數(shù).則

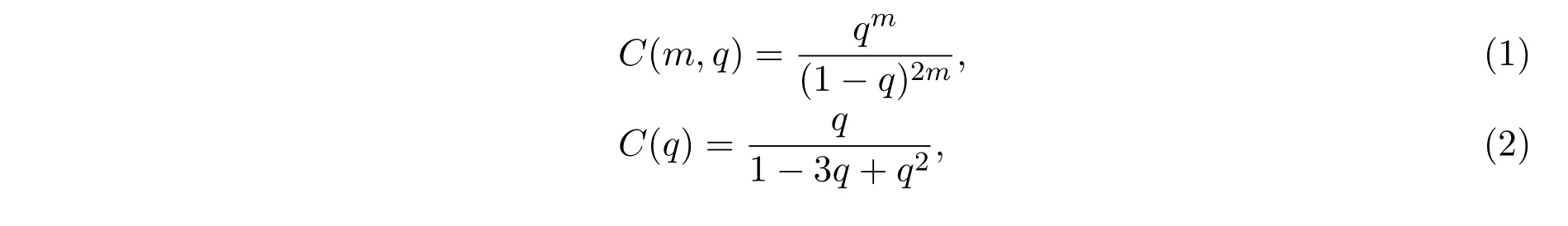
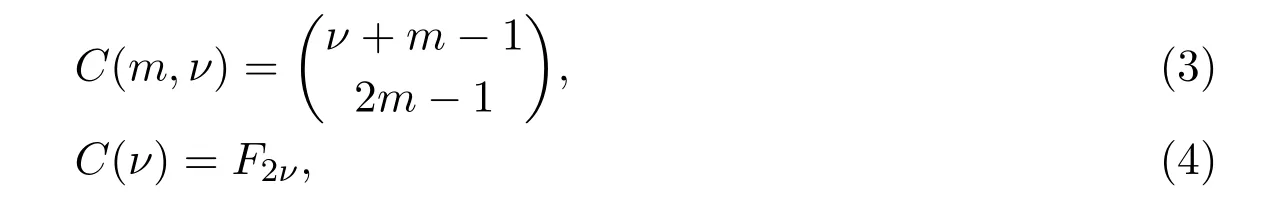
其中,Fn表示第n個(gè)Fibonacci數(shù).

文獻(xiàn)[4]利用正整數(shù)有序分拆和無序分拆的關(guān)系以及菲波拉契數(shù)與n-colour有序分拆的關(guān)系給出了n-colour有序分拆的一些組合性質(zhì).在這一節(jié)中,將利用菲波拉契數(shù)以及文獻(xiàn)[5]給出的正整數(shù)不含分部量1的有序分拆的組合性質(zhì)給出n-colour有序分拆的兩個(gè)組合性質(zhì).首先給出下面引理.

于是,得到ν的n-colour有序分拆的兩個(gè)組合性質(zhì):

定理 3.1 正整數(shù)ν的n-colour有序分拆數(shù)等于2ν+1不含分部量1的有序分拆數(shù).

證明 由引理3.2知2ν+1不含分部量1的有序分拆數(shù)等于第2ν個(gè)菲波拉契數(shù)F2ν,又由引理3.1的(4)式可知ν的n-colour有序分拆數(shù)等于F2ν,故正整數(shù)ν的n-colour有序分拆數(shù)等于2ν+1不含分部量1的有序分拆數(shù).

由引理3.3和定理3.1就得到下面的性質(zhì):

定理 3.2 正整數(shù)ν的n-colour有序分拆數(shù)等于最大分部量是2ν+1,各分部量≠1且相鄰分部量之差≥2的無序分拆數(shù).

證明 由引理3.3知2ν+1不含分部量1的有序分拆數(shù)等于最大分部量為2ν+1,各分部量≠1且相鄰分部量之差≥2的無序分拆數(shù),又由定理3.1可知2ν+1不含分部量1的有序分拆數(shù)等于正整數(shù)ν的n-colour有序分拆數(shù),故正整數(shù)ν的n-colour有序分拆數(shù)等于最大分部量是2ν+1,各分部量≠1且相鄰分部量之差≥2的無序分拆數(shù).

[1]MacMahon P A.Memoir on the compositions of numbers[J].Philos.Trans.Roy.Soc.London A,1894, 184:835-901.

[2]Andrews G E.The Theory of Partitions[M].Cambridge:Cambridge University Press,1998.

[3]Alladi k.A Variation on a theme of Sylvester-a smoother road to Gollniz(Big)theorem[J].Discrete Math., 1999,196:1-11.

[4]Agarwal A K.An analogue of Euler′s identity and new combinatorial properties of n-colour compositions[J]. J.Computational and Applied Mathematics,2003,160:9-15.

[5]郭育紅.與正整數(shù)的無序分拆和有序分拆相關(guān)的一些恒等式[J].數(shù)學(xué)學(xué)報(bào),2007,50(3):707-710.

[6]黃鳳英,柳柏濂.與有序分拆相關(guān)的一些恒等式[J].數(shù)學(xué)學(xué)報(bào),2009,52(2):403-408.

[7]邢林燕,尤利華.與無序分拆和有序分拆相關(guān)的幾個(gè)新的恒等式 [J].西南師范大學(xué)學(xué)報(bào):自然科學(xué)版, 2010(1):20-23.

[8]Frobenius G.Uper die Charakter der Symmetrischen Gruppe[M].Berlin:Sitzber.Press,1900.

[9]Agarwal A K.Rogers-Ramanujian identities for n-color partitions[J].J.Number Theory,1988,28(3):299-305.

[10]Agarwal A K,Andrews G E.Rogers-Ramanujian identities for partitions with“N copies N”[J].J.Combin. Theory Ser-A,1987,45(1):40-49.

[11]Agarwal A K.n-colour compositions[J].Indian J.Pure Appl.Math.,2000,31(11):1421-1427.

Some identities are relative to compositions and two combinatorial properties of n-colour compositions

Guo Yuhong
(Department of Mathematics,Hexi University,Zhangye 734000,China)

This paper discusses some relations between partitions and compositions of integers.As main results, some identities between partitions and compositions are obtained.Further,two combinatorial properties of the n-colour compositions,involving Fibonacci numbers and the number of compositions of n in with no part 1 appearing,are also presented.

partitions identity,n-colour compositions,combinatorial property,Fibonacci number

O157

A

1008-5513(2012)05-0590-05

2011-10-10.

甘肅省高等學(xué)校研究生導(dǎo)師科研項(xiàng)目(200809-04);河西學(xué)院校長(zhǎng)基金(XZ2011-01).

郭育紅(1970-),碩士,副教授,研究方向：組合數(shù)論.

2010 MSC:05A17