徐 平,王 偉,林德福,王 江,杜運(yùn)理

(1.北京理工大學(xué)宇航學(xué)院,北京 100081;2.中國(guó)兵器科學(xué)研究院,北京 100081）

隨著現(xiàn)代國(guó)防科技的飛速發(fā)展,對(duì)武器裝備的要求越來(lái)越高,為了使武器裝備達(dá)到未來(lái)戰(zhàn)爭(zhēng)的要求,近年許多學(xué)者對(duì)最優(yōu)制導(dǎo)律進(jìn)行了深入研究,并取得了許多成果.這些最優(yōu)制導(dǎo)律基本可以分為以下3類:①考慮導(dǎo)彈過(guò)載限制和目標(biāo)機(jī)動(dòng)的最優(yōu)制導(dǎo)律[1-2];②考慮自動(dòng)駕駛儀動(dòng)力學(xué)的最優(yōu)制導(dǎo)律[3-5];③增加末端約束的最優(yōu)制導(dǎo)律[6-8].本文推導(dǎo)了一種考慮自動(dòng)駕駛儀動(dòng)力學(xué)和目標(biāo)機(jī)動(dòng)的最優(yōu)制導(dǎo)律,并分析了基于捷聯(lián)導(dǎo)引頭這種最優(yōu)制導(dǎo)律的實(shí)現(xiàn)方案.捷聯(lián)導(dǎo)引頭相對(duì)于框架式導(dǎo)引頭主要擁有以下優(yōu)勢(shì)[9]:①質(zhì)量和體積優(yōu)勢(shì),由于去掉了框架,使得導(dǎo)引頭的質(zhì)量和體積大大地減小,節(jié)約了寶貴的彈上空間;②最大跟蹤彈目視線角速度不受機(jī)械限制,可以跟蹤高機(jī)動(dòng)目標(biāo);③對(duì)導(dǎo)彈的過(guò)載不敏感;④相對(duì)于框架式導(dǎo)引頭而言成本低廉;⑤可靠性高.正是捷聯(lián)導(dǎo)引頭擁有以上的明顯優(yōu)勢(shì),所以捷聯(lián)導(dǎo)引頭技術(shù)受到了各國(guó)軍方的高度重視.研究基于捷聯(lián)導(dǎo)引頭的最優(yōu)制導(dǎo)律實(shí)現(xiàn)擁有非常重大的現(xiàn)實(shí)意義.

1 最優(yōu)制導(dǎo)律推導(dǎo)

在推導(dǎo)最優(yōu)制導(dǎo)律前,先做以下幾個(gè)假設(shè):①導(dǎo)彈自動(dòng)駕駛儀可以用一個(gè)二階欠阻尼環(huán)節(jié)表示;②在制導(dǎo)過(guò)程中目標(biāo)以常值過(guò)載做機(jī)動(dòng);③忽略除導(dǎo)彈自動(dòng)駕駛儀以外所有環(huán)節(jié)的動(dòng)力學(xué).圖1給出了基于以上假設(shè)的簡(jiǎn)化制導(dǎo)系統(tǒng)原理框圖.其中aT表示目標(biāo)過(guò)載,aL表示彈體過(guò)載,˙aL表示彈體過(guò)載對(duì)時(shí)間的一階導(dǎo)數(shù),¨aL表示彈體過(guò)載對(duì)時(shí)間的二階導(dǎo)數(shù),aC表示過(guò)載指令,y表示導(dǎo)彈位置誤差,˙y表示導(dǎo)彈速度誤差,¨y導(dǎo)彈過(guò)載誤差,Tm表示自動(dòng)駕駛儀的時(shí)間常數(shù),μm表示自動(dòng)駕駛儀的阻尼系數(shù).

根據(jù)圖1可得

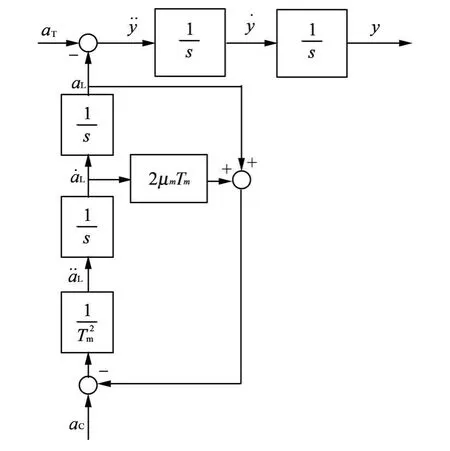
圖1 簡(jiǎn)化制導(dǎo)系統(tǒng)原理框圖F ig.1 Simplified guidancesystem p rinciple block diagram

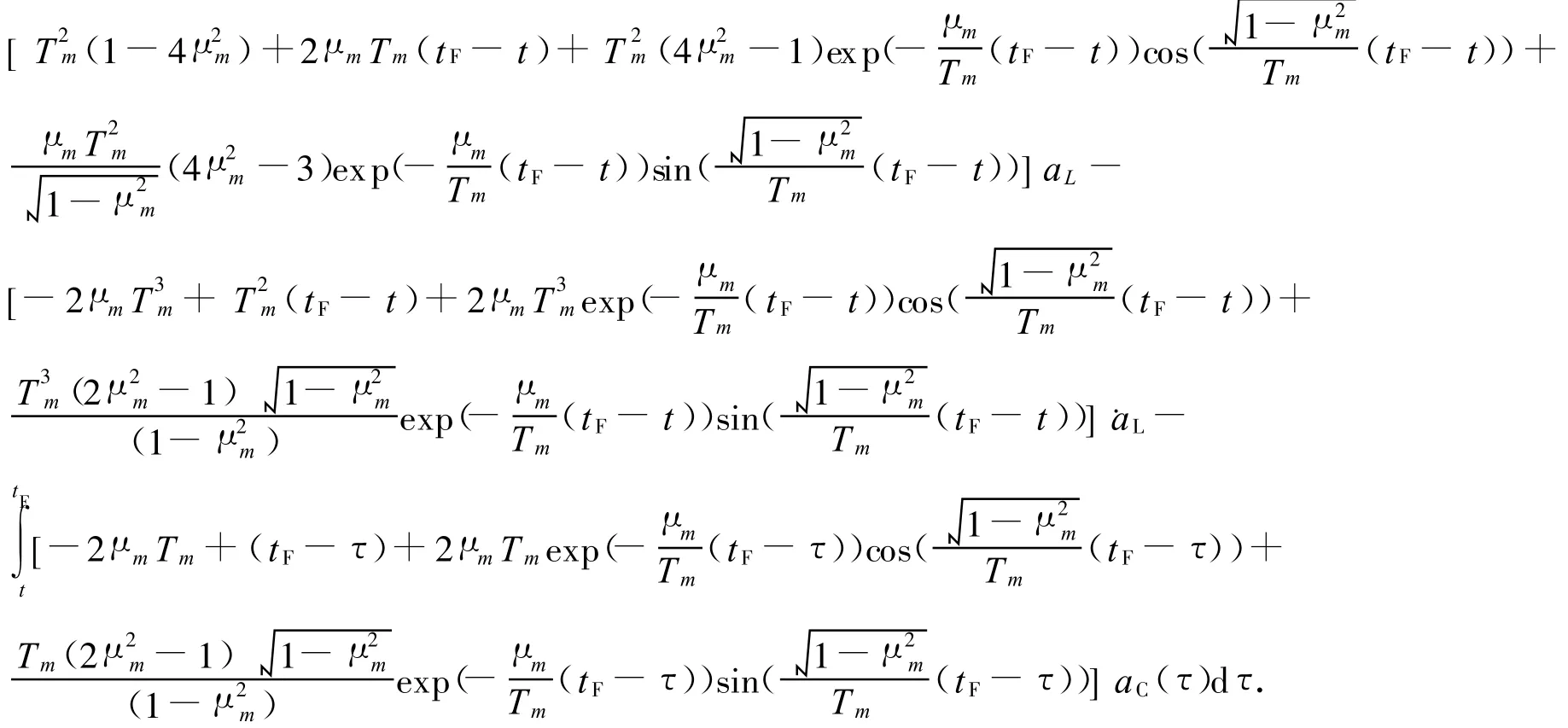
最優(yōu)制導(dǎo)律是一種使導(dǎo)彈以最小的控制能量準(zhǔn)確命中目標(biāo)的控制策略,根據(jù)以上結(jié)果運(yùn)用最優(yōu)制導(dǎo)律的這一原則可得最優(yōu)制導(dǎo)律如(1)式所示,其中˙q表示彈目旋轉(zhuǎn)角速度,v表示彈目接近速度.

2 基于捷聯(lián)導(dǎo)引頭最優(yōu)制導(dǎo)系統(tǒng)模型的建立

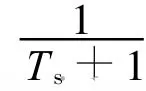
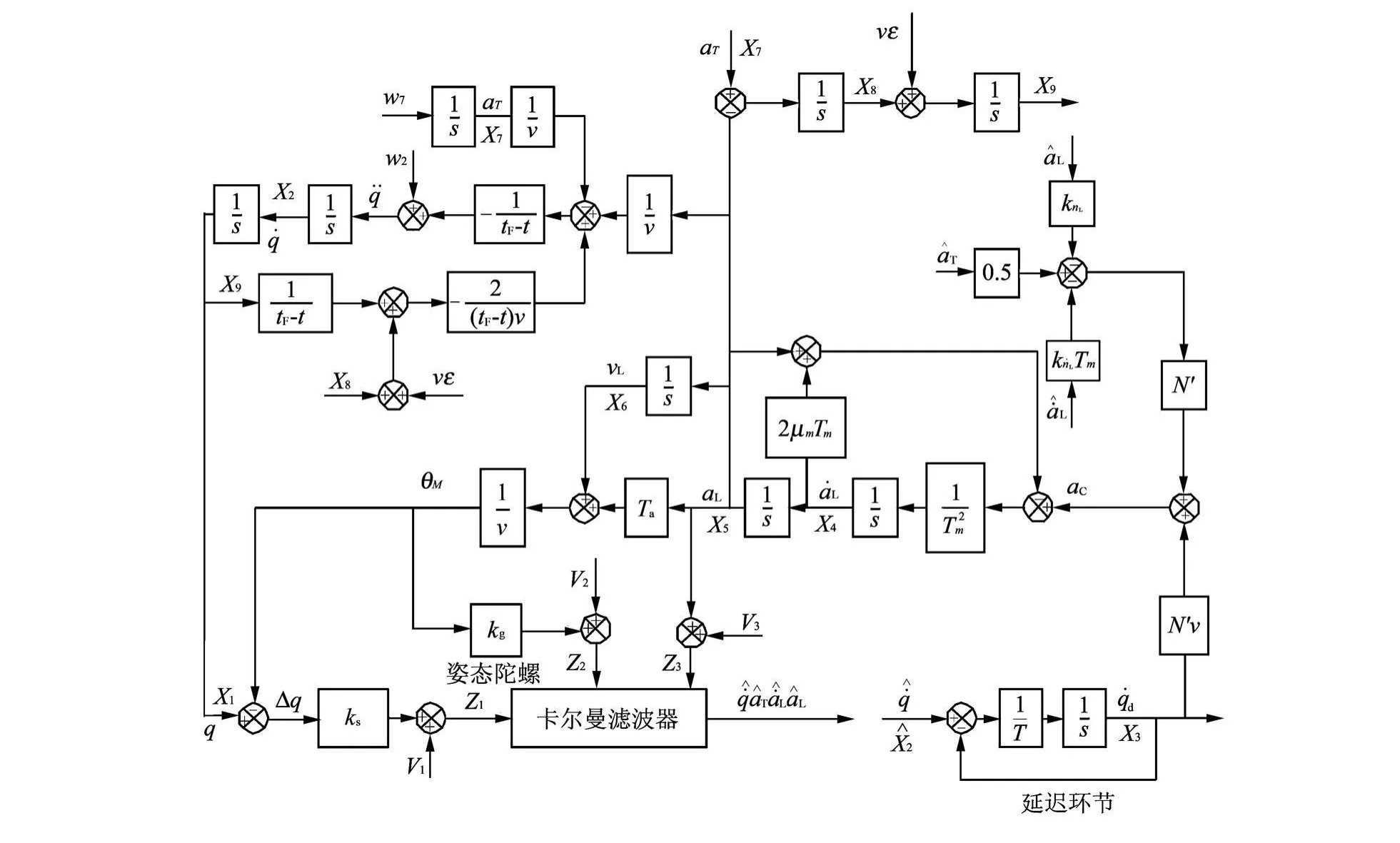
圖2 基于捷聯(lián)導(dǎo)引頭最優(yōu)制導(dǎo)系統(tǒng)框圖Fig.2 Optimal guidance system based on strapdown seeker block diagram

由圖2可得系統(tǒng)狀態(tài)方程為

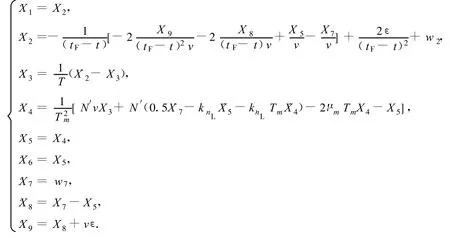
系統(tǒng)量測(cè)方程為

3 仿真分析

3.1 卡爾曼濾波器公式

由式(2)表示的系統(tǒng)的卡爾曼濾波公式如下[13]:

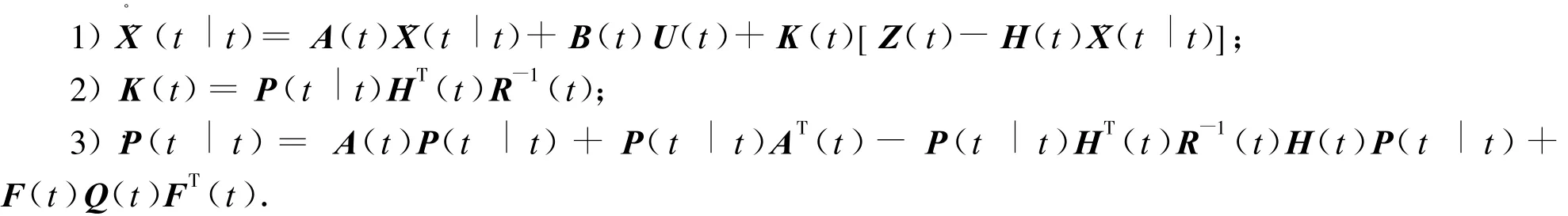
3.2 仿真算例

設(shè)制導(dǎo)初始時(shí)刻存在瞄準(zhǔn)誤差角 ε,目標(biāo)以加速度a T做機(jī)動(dòng).取T=0.02 s,N=3,v=220m/s,μm=0.1,Tm=0.08 s,k s=1.0,k g=1.0,a T=10m/s,ε=10°.取系統(tǒng)干擾噪聲的功率譜密度矩陣

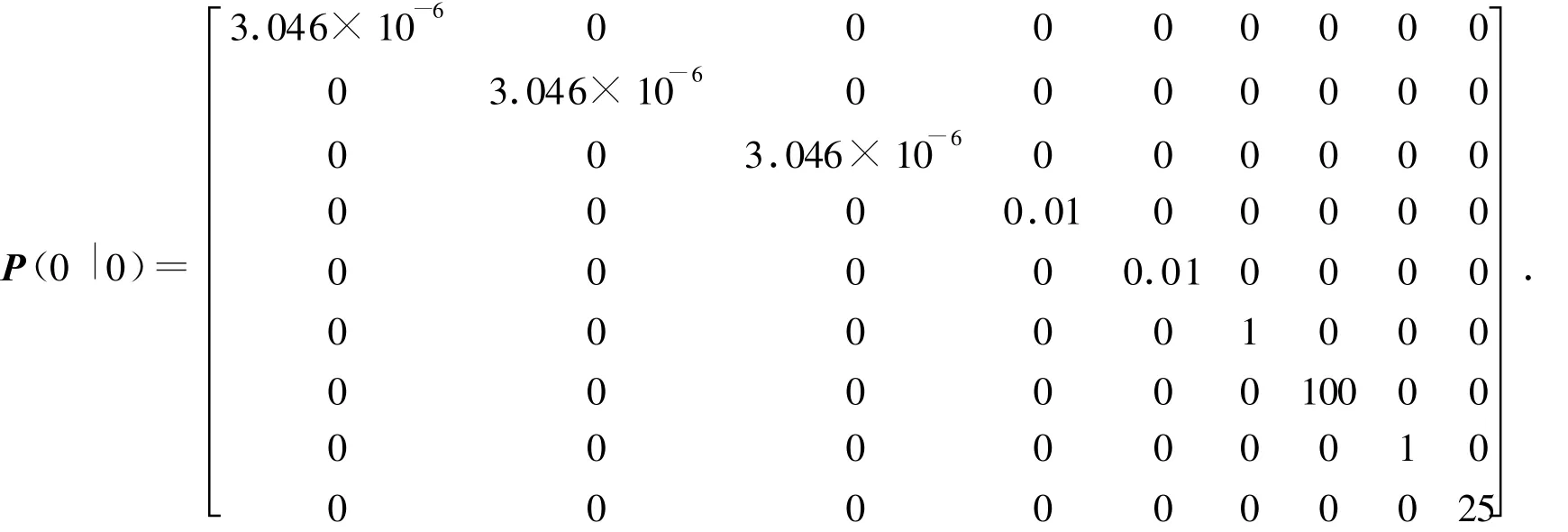
圖3給出了卡爾曼濾波器輸出的彈目視線角速率估計(jì)值和實(shí)際彈目視線角速率值的對(duì)比曲線,由圖3可以知,卡爾曼濾波器可以快速準(zhǔn)確地估計(jì)彈目視線角速率.圖4給出了卡爾曼濾波器輸出的目標(biāo)機(jī)動(dòng)過(guò)載與目標(biāo)實(shí)際機(jī)動(dòng)過(guò)載的對(duì)比曲線,由圖4可以看出,卡爾曼濾波器最后可以準(zhǔn)確地估計(jì)出目標(biāo)過(guò)載,但是需要一個(gè)較長(zhǎng)的過(guò)渡時(shí)間.

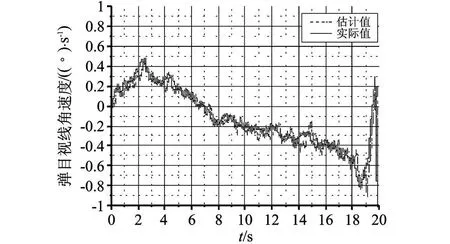
圖3 彈目視線角速率估計(jì)值與實(shí)際值對(duì)比曲線Fig.3 Curve of line of sight rate estimation value com pare w ith the actual value

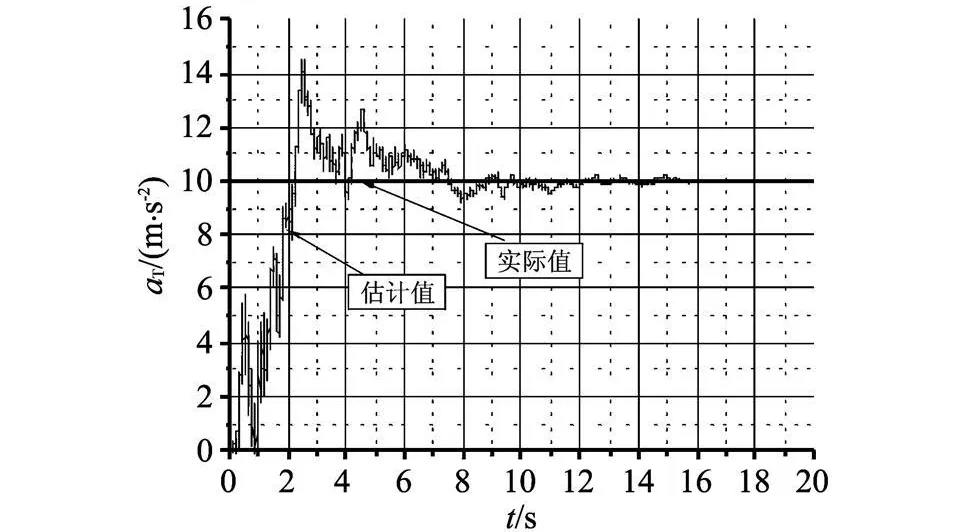
圖4 目標(biāo)過(guò)載估計(jì)值與實(shí)際值對(duì)比曲線Fig.4 Curve of target acceleration estim ation value compare with the actual value

圖5給出了使用最優(yōu)制導(dǎo)律和比例導(dǎo)引彈體的實(shí)際過(guò)載曲線對(duì)比,由圖5可以看出,采用最優(yōu)制導(dǎo)律彈體最大過(guò)載小于比例導(dǎo)引的最大過(guò)載,而且采用最優(yōu)制導(dǎo)律在制導(dǎo)末端彈體過(guò)載遠(yuǎn)小于采用比例導(dǎo)引制導(dǎo)律的情況.圖6給出了采用最優(yōu)制導(dǎo)律和采用比例導(dǎo)引的彈體位置誤差對(duì)比曲線,由圖6可以看出,采用最優(yōu)制導(dǎo)律的彈體位置誤差遠(yuǎn)小于采用比例導(dǎo)引時(shí)的情況.

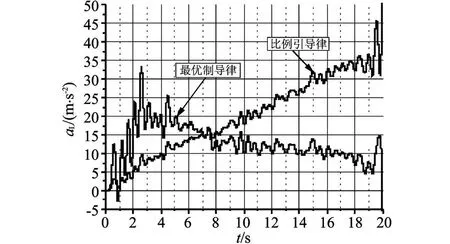
圖5 彈體過(guò)載對(duì)比曲線Fig.5 Missile acceleration com parison curve

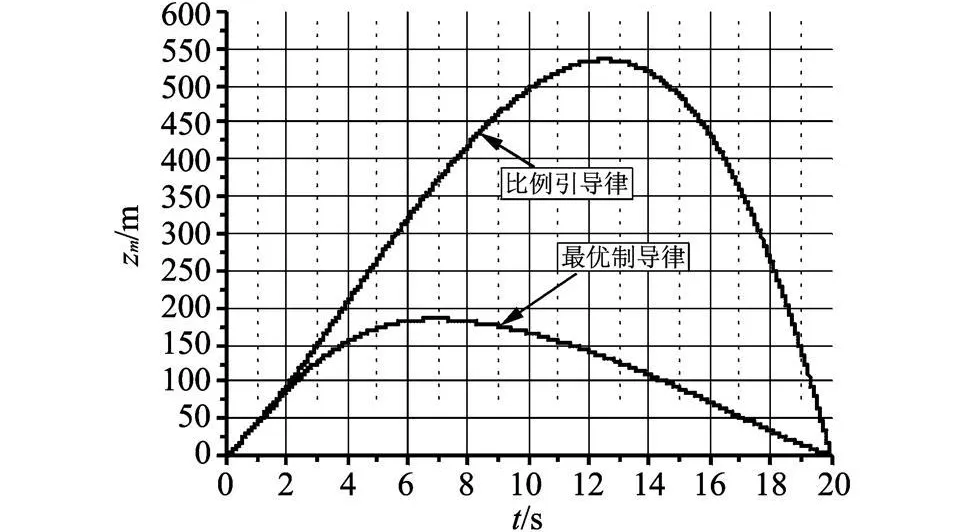
圖6 位置誤差對(duì)比曲線Fig.6 Position error comparison curve

4 結(jié)束語(yǔ)

本文推導(dǎo)了考慮目標(biāo)機(jī)動(dòng)和自動(dòng)駕駛儀動(dòng)力學(xué)的最優(yōu)制導(dǎo)律,并運(yùn)用卡爾曼濾波技術(shù)估計(jì)最優(yōu)制導(dǎo)律過(guò)載指令形成需要的狀態(tài),給出了一種基于捷聯(lián)導(dǎo)引頭的最優(yōu)制導(dǎo)律實(shí)現(xiàn)方案.仿真結(jié)果表明,雖然卡爾曼濾波器估計(jì)目標(biāo)過(guò)載的時(shí)候,過(guò)渡過(guò)程較長(zhǎng),但是采用了最優(yōu)制導(dǎo)律的導(dǎo)彈無(wú)論是在過(guò)載方面還是位置誤差方面都要遠(yuǎn)優(yōu)于采用比例導(dǎo)引的導(dǎo)彈.

[1] Hexner G,Pila A W.A p ractical stochastic optimalguidance law for a bounded acceleration m issle[J].A IAA,2010(8):54.

[2] 謝希權(quán),易華.主動(dòng)雷達(dá)型空空導(dǎo)彈最優(yōu)末制導(dǎo)律工程研究[J].系統(tǒng)工程與電子技術(shù),2000,22(12):66-68.

Xie Xiquan,YiHua.Study on optimal terminal guidance law for AAM[J].Systems Engineering and Electronics,2000,22(12):66-68.(in Chinese)

[3] 劉德忠,劉潔慧,朱曉東.二次型一階最優(yōu)制導(dǎo)律的一種實(shí)現(xiàn)方案[J].航空兵器,2007(6):3-5.

Liu Dezhong,Liu Jiehui,Zhu Xiaodong.Implementation of a sing le-lag optimal control guidance law[J].Aero Weaponry,2007(6):3-5.(in Chinese)

[4] 莊志洪,路建偉,丁慶海,等.一種基于二階制導(dǎo)系統(tǒng)的最優(yōu)導(dǎo)引律研究[J].南京理工大學(xué)學(xué)報(bào),1999,23(3):237-239.

Zhang Zhihong,Lu Jianwei,Ding Qinghai,etal.Performance analysis of oneop timal guidance law for2-orders system[J].Journal of Nanjing University of Science and Technology,1999,23(3):237-239.(in Chinese)

[5] Jalali-NainiSH.Modern explicit guidance law for high-order dynam ics[J].JGuidance,2004,27(5):918-922.

[6] Vitaly Shaferman,Tal Shima.Linear quadratic guidance laws for imposing a term inal intercept ang le[J].Journal of Guidance,Control,and Dynam ics,2008,31(5):1400-1412.

[7] 孫未蒙,鄭志強(qiáng).多約束條件下對(duì)地攻擊的最優(yōu)制導(dǎo)律[J].兵工學(xué)報(bào),2008,29(5):567-571.

Sun Weimeng,Zheng Zhiqiang.Op timal guidance law w ith mu ltip le constraints in ground strike[J].A cta Arm a Men Trail,2008,29(5):567-571.(in Chinese)

[8] 劉丹,祁載康.限制導(dǎo)彈落角和落點(diǎn)的最優(yōu)制導(dǎo)律[J].北京理工大學(xué)學(xué)報(bào),2001,21(3):278-281.

Liu Dan,Qi Zaikang.Impactangle and final position constrained optimal guidance law[J].Journal of Beijing Institute of Technology,2001,21(3):278-281.(in Chinese)

[9] Captain Thomas,Callen R.Guidance Law Design For TacticalW eaponsW ith StrapDown Seekers[J].A IAA,1979,1732:161-180.

[10] Paul L Vergez.Linear Op timal Guidance for an AIM-9L Missile[J].JGuidance and Control,1981,4(6):662-663.

[11] Gordon K F Lee.Estimation of the Time-to-Go Parameter for Air-to-Air Missile[J].JGuidance,1985,8(2):262-266.

[12] Chang-Kyung Ryoo,Min-jea Tahk,Hangju Cho.Practical Time-to-Go Estimation Methods for Optimal Guidance[J].AIAA,1999,4143:29-37.

[13] G rewalM S,Andrew s A P.Kalman Filtering Theory and Practice[Z].Prentice Hall:Englewood Cliffs,New Jersey,1993.