WANG Xiao-ping,GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

The Derivation A lgebra of the Schrdinger-Viraso ro Lie A lgebra*

WANG Xiao-ping,GAO Shou-lan

(Faculty of Science,Huzhou Teachers College,Huzhou 313000,China)

Fo r the perfect Lie algebra w ith one-dimensional center at lest,there is not a general result about the relationship between its derivation algebra and that of its universal central extension.In this paper,we determine the derivation algebra of the Schr?dinger-Viraso ro Lie algebra L,w hich is the universal central extension of the Schrdinger-Virasoro Lie algebraw ith one-dimensional center.It is p roved that L has only one outer derivation,w hilehas three outer derivations[1].Hence,we get one examp le that the derivation algebra of the universal central extension of a Lie algebra,the center of w hich is not zero,is not isomorphism to that of the Lie algebra.

Schrdinger-Virasoro algebra;central extension;derivation

MSC 2000:17B40

0 In troduction

The Schr?dinger-Viraso ro Lie algebra,o riginally introduced by M.Henkel in[2]during his study on the invariance of the free Schr?dinger equation,is a vecto r space over the comp lex field C w ith a basisand the Lie brackets:

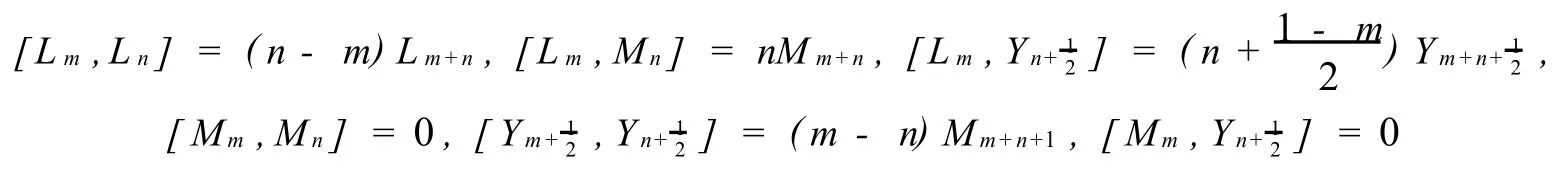
for all m,n∈Z.Due to its important app lications in many areas of Mathematics and Physics,the structure and rep resentation theory ofhave been extensively studied.For examp le,M.Henkel investigated thathasone-dimensional universal central extension in[2].C.Roger and J.Unterberger p resented a detailed cohomological study and determinedhas three outer derivations[1].And the automorphism group ofis determined in[3].Nowadays,extensions and generalizations related to the Schr?dinger-Virasoro algebra have appeared and their structure and rep resentation theory have been extensively studied,such as[4]～[6].

The derivation algebra of a centerless perfect Lie algebra is isomorphism to that of the universal central extension of the Lie algebra[7].While for the perfect Lie algebra w ith one-dimensional center at lest,there is not a general result about the relationship between its derivation algebra and that of its universal central extension.In this paper,we determine the derivation algebra of the Schr?dinger-Virasoro Lie algebra L,w hich is the universal central extension of the Schr?dinger-Virasoro Lie algebraw ithone-dimensional center.It show s that L has only one outer derivation,w hilehas three outer derivation[1].Therefo re,the derivation algebra of L is not isomo rphism to that of.

Throughout the paper,we denote by Z and C*the set of integers and the set of non-zero comp lex numbers respectively,and all the vector spaces are assumed over the comp lex field C.

1 The Derivation Algebra of L

[1]ROGER C,UN TERBERGER J.The Schrdinger-Viraso ro Lie group and algebra:Rep resentation theo ry and cohomological study[J].Annales Henri Poincar,2006(7～8):1477～1529.

[2]HENKEL M.Schrodinger invariance and strongly anisotropic critical systems[J].J Stat Phys,1994,75:1023～1061.

[3]GAO S.The automorphism group of the Schr?dinger-Virasoro Lie algebra[J].Journal of Huzhou Teachers College,2010,32:1:6～10.

[4]GAO S,JIANG C,PEI Y.Structure of the extended Schr?dinger-Viraso ro Lie algebra[J].A lgebra Colloq,2009,16:4 549～566.

[5]L IJ,SU Y.Rep resentations of the Schrodinger-Viraso ro algebras[J].J Math Phys,2008,49,053512:14.

[6]UNTERBERGER J.On vertex algebra rep resentations of the Schr?dinger-Viraso ro Lie algebra[EB/OL].[2007-03-21].arXiv:cond-mat/0703214v2.

[7]BEN KART G,MOODY R.Derivations,central extensions and affine Lie algebras[J].A lgebras Groups Geom,1986,3(4):456～492.

[8]FARNSTEINER R.Derivations and extensions of finitely generated graded Lie algebras[J].J Algebra,1988,118(1):34～45.

MSC 2000:17B40

王曉萍,高壽蘭

(湖州師范學(xué)院理學(xué)院,浙江湖州313000)

對(duì)于中心非零的perfect李代數(shù),關(guān)于它的泛中心擴(kuò)張的導(dǎo)子代數(shù)與它本身的導(dǎo)子代數(shù)之間的關(guān)系尚未有一個(gè)一般的結(jié)論.通過計(jì)算帶有一維中心的 Schr?dinger-Virasoro李代數(shù)的泛中心擴(kuò)張L的導(dǎo)子,證明了L只有一個(gè)外導(dǎo)子,而由文獻(xiàn)[1]知有三個(gè)外導(dǎo)子,從而得到了一個(gè)中心非零的perfect李代數(shù)的導(dǎo)子代數(shù)與其泛中心擴(kuò)張的導(dǎo)子代數(shù)不同構(gòu)的例子.

Schrodinger-V iraso ro李代數(shù);中心擴(kuò)張;導(dǎo)子

O152.5

O152.5 Document code:A Article ID:1009-1734(2010)02-0022-05

date:2010-01-21

Biography:WANG Xiao-ping,Undergraduate student of grade 2006,Faculty of Science,Huzhou Teachers College,

Research Interests:Lie algebra.