An underdamped and delayed tri-stable model-based stochastic resonance
Yan-Fei Jin(靳艷飛), Hao-Tian Wang(王昊天), and Ting-Ting Zhang(張婷婷)
Department of Mechanics,Beijing Institute of Technology,Beijing 100081,China
Keywords: stochastic resonance, underdamped tri-stable system, spectral amplification, time-delayed feedback
1.Introduction
The ambient noise can play a constructive role in the output of the nonlinear system under some conditions.The benefits of noise and nonlinearity lead to the classical stochastic resonance (SR) phenomenon.[1]It is known that the SR has been widely studied theoretically,numerically and experimentally in many fields over the past decades.[2–4]However,most SR studies focus on the first-order dynamical model describing overdamped motions,in which the inertia term is ignored for simple of theoretical analysis.In practice,many systems generally need to be described as the second-order underdamped dynamical models,where the damping coefficient plays an important role in the SR effect.[5–11]For example,it is shown that a specific damping can generate the largest enhancement in SR under Gaussian white noises[5]or trichotomous noises[6]in the coupled underdamped bi-stable systems.The non-monotonic dependence of SR measures,such as SNR and spectral amplification, on damping parameter is found in an underdamped bi-stable system driven by noise and different harmonic signals.[7,8]For the underdamped periodic potential system,[9–11]the average input energy is maximized with the proper damping parameter.Yet it is a fact that the consideration of inertia term leads to the difficulty in theoretical analysis of SR.It is thus necessary to develop some new methods to deal with the SR theoretical derivation of the second-order or high-dimensional dynamical systems.
Multi-stability refers to the coexistence of multiple stable equilibrium states in nonlinear dynamical systems, which has been observed in many mechanical systems such as multi-stable energy harvesters,[12,13]nonlinear vibrational isolators,[14]and multi-stable inflatable origami structures.[15]When noise is considered in multi-stable systems,some interesting phenomena such as noise-induced resonances,[16,17]attractor preference,[18]and attractor hopping[19]spring up.Especially,the study of SR in multi-stable systems has attracted widely attentions.[20–26]For example,Nicoliset al.[20,21]analyzed the phenomenon of SR in multi-stable systems through the linear response and information entropy.Xu and Jinet al.[22,23]studied the noise-induced resonances in the Josephson junction and triple-well potential respectively, where the constructive effects of trichotomous noises and friction memory are explored.Zhanget al.[24]studied the logical SR induced by additive or multiplicative colored noise in the triplewell potential systems.Arathiet al.[25]reported that signalto-noise ratio(SNR)can attain its maximum in the triple-well potential with a uniform depth.Jinet al.[26]studied SR and mean-first passage time of a quad-stable potential, which is applied to the fault diagnosis of inner and outer race bearing.
The time-delayed state feedback control is one of feasible methods of controlling unstable and chaotic motions by designing feedback gains and time delays.[27–29]However,the infinite dimensions of the solution space produce a hard problem to the theoretical treatment of stochastic delay differential equations (SDDEs).Some approaches such as the approximate Fokker–Planck equation[30]and the extended semidiscretization method[31]have been proposed to deal with SDDEs.Moreover, SR has been investigated in the dynamical system with time delay.[32–36]Tsimringet al.[32]proposed the SR theory of a delayed bi-stable system under the twostate system approximation.Jinet al.[33,34]studied the noiseinduced resonances in the delayed bi-stable and tri-stable systems driven by correlated additive and multiplicative noises.Xuet al.[35]found the correlation between the multiplicative and additive noises can induce stochastic multi-resonance phenomenon and noise-enhanced stability in a delayed triple-well potential.To the knowledge of authors,less attention has been paid to the SR in a second-order tri-stable system with timedelayed feedback control and colored noise.
The main purpose of this study is to derive the analytical expression of the spectral amplification and analyze the SR in an underdamped tri-stable system with both displacement and velocity delayed states feedback and colored noise.In Section 2,an underdamped tri-stable system with displacement and velocity delayed states feedback is modeled, which is driven by colored noise and a periodic signal.The stationary probability density(SPD)is obtained analytically by using the improved energy envelope stochastic average method.In Section 3, the analytical expression of the spectral amplification is derived to describe the SR phenomenon.The effects of noise intensity,damping coefficient and time delay on SR are discussed.Finally,some conclusions are drawn in Section 4.
2.An underdamped tri-stable system with delayed state feedback
In this study, the system of concern is an underdamped Brownian particle in a tri-stable potential with the displacement and velocity delayed states feedback.The corresponding Langevin equation is governed by
wherexτ=x(t ?τ), ˙xτ= ˙x(t ?τ),γis the damping coefficient,βandνare the feedback gains,τ ≥0 is the time delay in the paths of displacement feedback and velocity feedback.εandωare the amplitude and frequency of the periodic signal.Theη(t)denotes a Gaussian colored noise with the following statistical properties:[12]
whereDis noise intensity andτ1is correlation time of the colored noise.The colored noiseη(t)in Eq.(1)can be obtained through a first-order low-pass filter by passing Gaussian white noiseW(t)as the following form:
where〈W(t)〉=0,〈W(t)W(s)〉=2Dδ(t ?s).δis the Dirac delta function.
The potential functionU0(x)in Eq.(1)has the following form:
where the parametersb,c,hare positive.From Eq.(2), the equilibrium points ofU0(x)are easily found
where(xmi,0)(i=1,2,3)denote stable equilibrium points and(xn j,0)(j=1,2)denote unstable equilibrium points.In Fig.1,U0(x)is plotted for fixedh=1,b=0.9,andc=0.6.It is seen thatU0(x)has the triple-well potential structure.
2.1.Stationary probability density
To obtain the SPD of Eq.(1), the generalized harmonic function is introduced and the system states can be expressed as
whereA(H) represents the energy-dependent amplitude,ω(H) denotes the energy-dependent frequency,xmi(H)(i=1,2,3) represents the stable equilibrium points as displayed in Fig.1.
Based on the transformation (3), the time-delayed displacement and velocity feedback control terms in Eq.(1)can be expressed approximately as
Substituting Eq.(4) into Eq.(1) leads to the following equation:
where
According to Eq.(5),one can get the equivalent potential function and total energy function as
From Eqs.(5)and(6),it is seen that theω(H)depends on the system energy (8).Thus, for a given energy levelH, one can get the energy-dependent period
and the energy-dependent frequencyω(H)=2π/T(H)by the iteration method due to the existence of the unknownω(H)inU(X).That is,
where the minimum and maximum vibrating displacementsx1andx2are determined by equationH=U(A) for the system without delayed states feedback.
Figure 2 shows the calculated total energy and different energy-dependent frequency for different steady states of potential function.At the three stable equilibrium points(xm1,0),(xm2,0),(xm3,0),the total energyHreaches a local minimum while the energy-dependent frequencyω(H) exhibits a local maximum.It is observed that the local maximum ofω(H)at the left-side and right-side stable equilibrium point is larger than that at middle stable point.
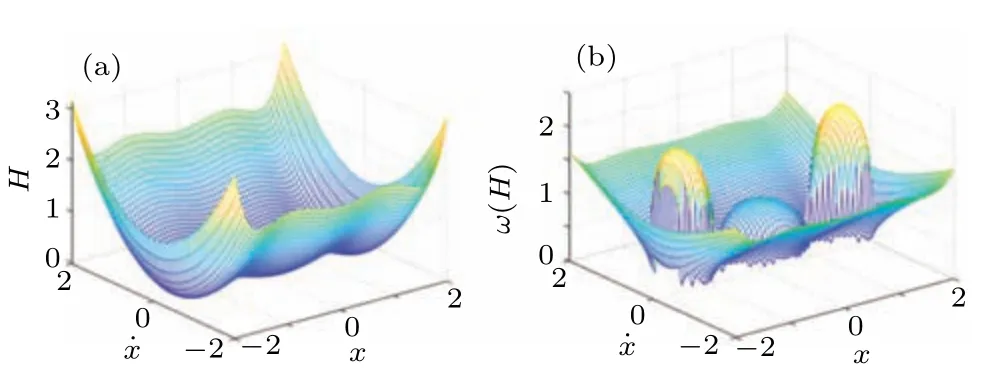
According to Eq.(8),equation(5)can be rewritten as
HereH(t)is an approximate Markovian process,then the It?o equation for the limiting diffusion processH(t)can be expressed as
whereB(t)is a standard Wiener process,m(H)andσ(H)respectively represent the drift and diffusion coefficients
where the time averaging
The closed-loop integration is carried out corresponding to different energy levels.Especially,when the motion is moving in the right-side or left-side potential well,one has
Based on Eqs.(12)and(13),the SPD of the total energyH(t)can be derived as
where theNis a normalization constant.
Considering the formula
and Eq.(14),the joint SPD of system(5)can be obtained as
From Eq.(15), the expression of generalized potential function is given as
2.2.The effects of system parameters on SPD
It is shown that there is enough time for the tristable system to reach the local equilibrium point during the period of 1/?.[14]Thus, the effects of colored noise, damping coefficient, and delayed states feedback on the joint SPD (15) are analyzed as following by ignoring the periodic excitation(i.e.,ε=0).
Figure 3 shows the effects of feedback gains and time delay on the joint SPD.In Fig.3(a), the shape of the joint SPD displays a triple-peak structure,which indicates the system has a transition motion among three inter-wells.With the increase of displacement feedback gainβin Fig.3(b),the middle peak of the joint SPD decreases while the peaks on left and right sides increase.That is, the system mainly performs a motion between the left and right potential well, whose dynamical behaviors are similar to those of bistable system.When the velocity feedback gainυis increased,compared with that in Fig.3(a), figure 3(c) shows the height of middle peak decreases slightly.When the time delay is increased in Fig.3(d),the joint SPD is a trimodal structure with a uniform depth for the triple-well potentials.In a word,the time delay and feedback gains play an important role in the shapes of the joint SPD, which can be used to adjust the system structure for achieving the desired dynamics.
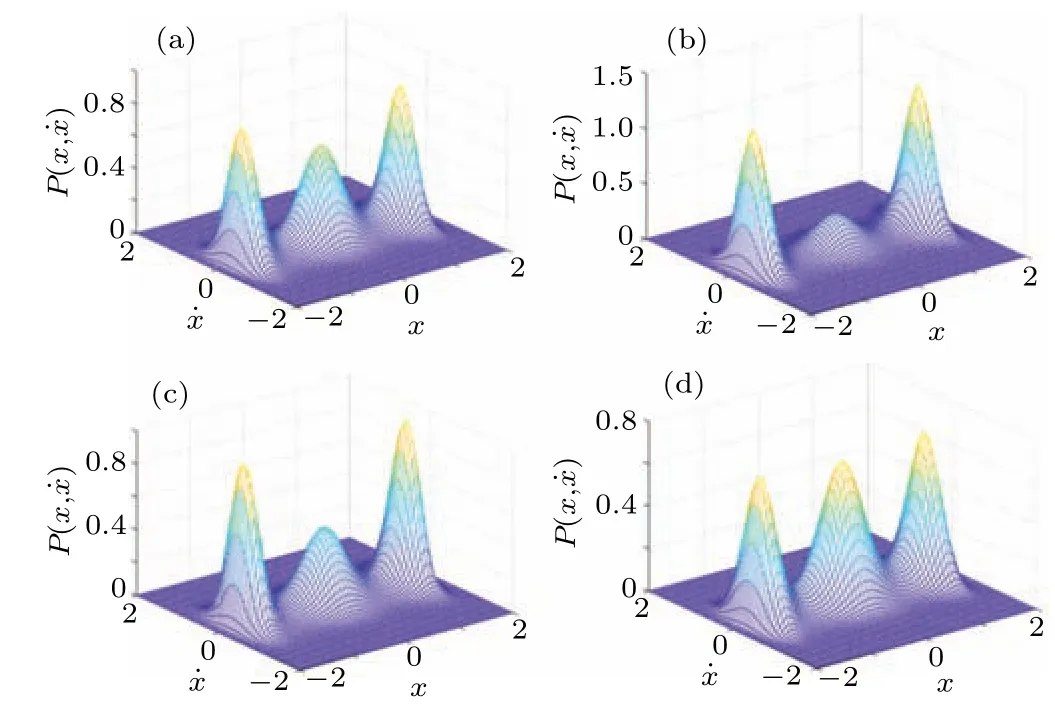
Fig.3.The effects of feedback gains and time delay on the joint SPD: (a)β =0.01,υ =0.01,τ =0.1;(b)β =0.1,υ =0.01,τ =0.1;(c)β =0.01,υ=0.1,τ=0.1;(d)β =0.01,υ=0.01,τ=1.5.The other parameters are chosen as c=0.6,τ1=0.1,D=0.1,γ =1.
The plots of joint SPD with different noise intensity,noise correlation time,and damping coefficient are demonstrated in Fig.4.The following conclusions are obtained mainly by comparing with Fig.3(a).From Fig.4(a), it is seen that the increase of correlation timeτ1results in the decrease of middle peak in joint SPD.The system spends most time in the left and right sides potential wells.In Fig.4(b),the heights of three peaks in joint SPD tend to the same as the noise intensityDincreases.That is,noise intensity of colored noise can strengthen the inter-well transition.Figure 4(c)shows that the decrease of damping coefficientγleads to a trimodal structure with a uniform depth for the tristable potentials.This phenomenon is in line with the physical intuition because the particles are increased their energy very rapidly and released from the potential wells for small damping coefficient.To verify the theoretical result (15), the MCS of Eq.(1) with the same parameters as Fig.4(c)is given in Fig.4(d).It is obvious that the theoretical and numerical results coincide very well.
3.Stochastic resonance
Based on the generalized potential function (16) and the linear response theory, the analytical expression of the spectral amplification will be derived and the influents of system parameters on SR will be discussed in the following subsections.
3.1.Spectral amplification
Let ˙x=y,equation(5)can be rewritten as
Equation (17) can be considered as a discrete-state Markov process describing the transfer of probability massespi(i=1,2,3)within the adiabatic approximation.The corresponding master equation is derived as
in which
The expressions of(i= 1,2,3) and(j= 1,2) in Eqs.(20)–(23)can be determined by
where the(i=1,2,3)are eigenvalues of the linearization matrix of Eq.(17)on stable states(xmi,0)(i=1,2,3)and the(j=1,2) are eigenvalues of the linearization matrix of Eq.(17)on unstable points(xn j,0)(j=1,2).
For the small signal amplitudeε,the first-order approximation ofPcan be expressed as
where Δpiis the first-order correction topi.
Expanding the transfer matrixW=W0+εΔWcosωtand substituting Eq.(26) into Eq.(18) leads to the following expressions:
whereW0and(i=1,2,3)are the transition rate matrix and probability for system without periodic signal, respectively.The(i= 1,2,3;l= 1,2,3) are the corresponding element of matrixW0and theσ0i(i=1,2,3)are the element of three-dimensional column vectorσ0.That is,
The solution of Eq.(27)has the following form for considering the limit of long time:
Substituting Eq.(28)into Eq.(27),one has
whereκkandζkare the eigenvalues and the eigenvectors ofW0,respectively.Theαk(k=1,2,3)are the expansion coefficients of vectorσ0of Eq.(27)in the basis ofζk.In general,σ0can be expressed as
According to Eq.(28), the steady-state response of system(17)can be derived as follows:
Based on Eq.(29), the spectral amplificationη=(V/ε)2is obtained as
In the following analysis,the spectral amplificationηis used to characteristic the SR phenomenon when the plot ofηdisplays a non-monotonic behaviorversusnoise intensity.
3.2.The effects of system parameters on SR
The effects of time delay and feedback gains on the spectral amplificationηand SR are shown in Fig.5.In Fig.5,the curves ofη versus Dshow a single-peak structure and the SR phenomenon is observed.In Figs.5(a) and 5(b), the curves ofηare plotted for the case of time-delayed displacement feedback and time-delayed velocity feedback respectively.For both cases,the maximum peak value ofηappears in the system with negative feedback gain, which means that the negative feedback gain tends to strengthen SR phenomenon for fixedτ.However,the SR effect for positive feedback gain case is even worse than that without feedback control as shown in Figs.5(a)and 5(b).Figures 5(c)and 5(d)display the effects of time delay on SR in the system with displacement and velocity delayed states feedback.A comparison between Figs.5(c)–5(d) and 5(a)–5(b) illustrates that the value of resonant peak increases when both displacement and velocity time-delayed feedback control are considered.With the increase ofτ, the SR peak increases for negative velocity feedback gain (i.e.,υ <0);while it decreases with increasingτfor positive velocity feedback gain(i.e.,υ >0).In other words, the SR effect and control performance can be enhanced by choosing appropriate combination of time delay and feedback gain.
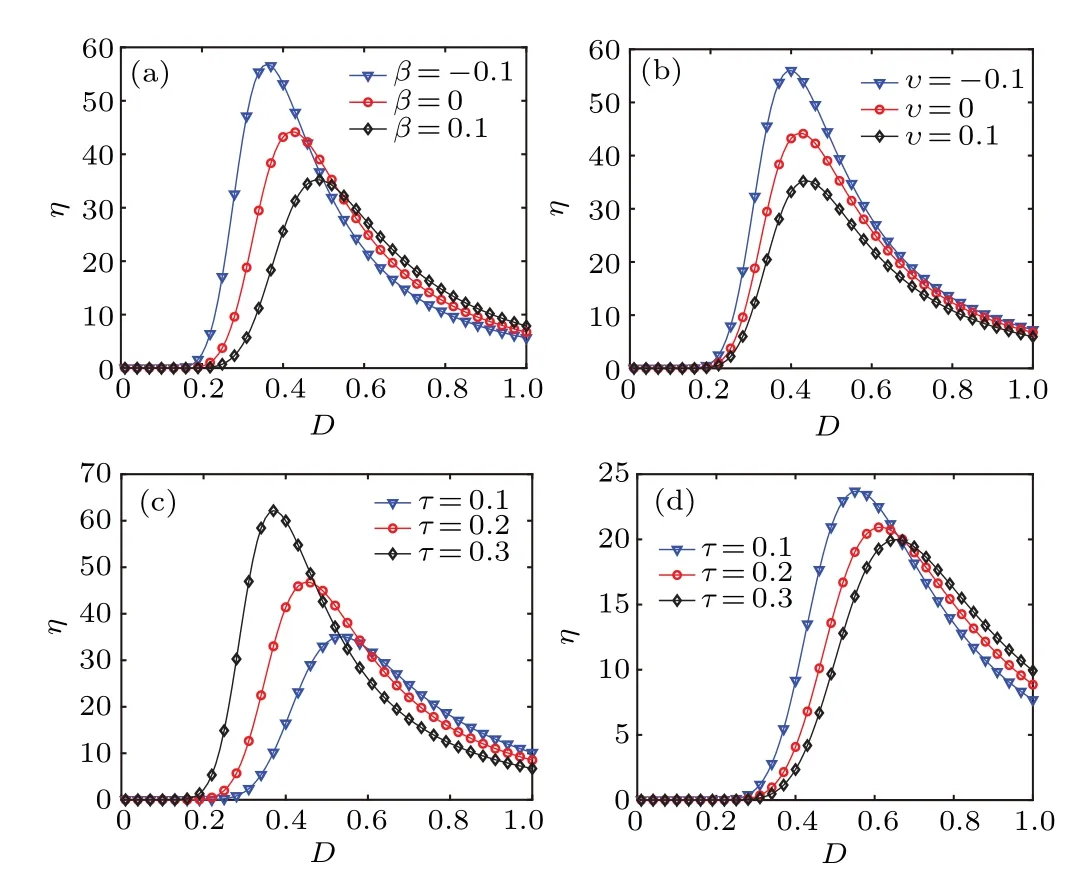
Fig.5.The spectral amplification η versus noise intensity D with different values of β,υ,and τ: (a)υ =0,τ =0.1; (b)β =0,τ =0.1; (c)β =0.2,υ=?0.1;(d)β =0.2,υ=0.1.The other parameters are chosen as c=0.4,τ1=0.1,γ =1.
Figure 6 depicts the curves of the spectral amplificationηas a function of noise intensityDfor different correlation time and damping coefficient.It is observed that the curve exhibits a maximum at the optimal noise intensity, where the SR appears.From Fig.6(a),the peak value is decreased while the optimal noise intensity increases with increasing correlation time of noise.That is, the SR effect is suppressed by correlation time.In Fig.6(b), the increasing damping coefficient decreases the SR peak value and increases the optimal noise intensity.This phenomenon can be understood as the big damping hinders the system from transiting among the potential wells.Thus,the system needs to overcome this hinderance by increasing the noise intensity.
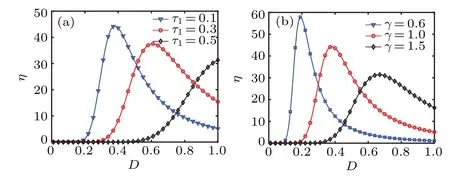
Fig.6.The spectral amplification η versus noise intensity D with different values of τ1 and γ: (a)γ =1;(b)τ1=0.1.The other parameters are chosen as c=0.4,β =?0.1,υ =0.1,τ =0.1.
4.Conclusions
In this paper,the displacement and velocity delayed states feedback are considered in an underdamped tri-stable model,which is driven by colored noise and a periodic signal.To explore the SR phenomenon, the stochastic averaging based on energy-dependent frequency is proposed to tackle the theoretical treatment of SR in the SDDE.The analytical expressions for SPD and spectral amplification are derived.The effects of noise intensity,damping coefficient and time-delayed feedback on SPD are discussed.It is found that the shape of joint SPD depends on the time delay,feedback gains and correlation time.Especially, the joint SPD is a trimodal structure with a uniform depth by choosing proper time delay and feedback gains.At the optimal noise intensity,the curve of spectral amplification shows a single-peak structure and SR phenomenon is observed.When the time delay increases, the SR peak increases for negative velocity feedback gain and decreases for positive velocity feedback gain.That is, the SR effect and control performance can be improved through adjusting time delay and feedback gains.
In practice, numerous physical systems are subjected to randomly fluctuating excitation and time delay.The obtained results provide the reliable basis for studying the other noiseinduced behaviors in the tri-stable dynamical model with timedelayed feedback,such as coherence resonance and stochastic bifurcation.Furthermore,multi-stable characteristics are usually encountered in some physical devices and mathematical models.
Acknowledgements
Project supported by the National Natural Science Foundation of China(Grant No.12072025)and the Beijing Natural Science Foundation(Grant No.1222015).
- Chinese Physics B的其它文章
- Photophysics of metal-organic frameworks: A brief overview
- Anelasticity to plasticity transition in a model two-dimensional amorphous solid
- Ab initio nonadiabatic molecular dynamics study on spin–orbit coupling induced spin dynamics in ferromagnetic metals
- Ultrafast dynamics in photo-excited Mott insulator Sr3Ir2O7 at high pressure
- Universal basis underlying temperature,pressure and size induced dynamical evolution in metallic glass-forming liquids
- Valley filtering and valley-polarized collective modes in bulk graphene monolayers

