Ultrafast dynamics in photo-excited Mott insulator Sr3Ir2O7 at high pressure
Xia Yin(尹霞), Jianbo Zhang(張建波), Wang Dong(王東), Takeshi Nakagawa, Chunsheng Xia(夏春生),Caoshun Zhang(張曹順), Weicheng Guo(郭偉程), Jun Chang(昌峻), and Yang Ding(丁陽),?
1Center for High-Pressure Science and Technology Advanced Research,Beijing 100094,China
2College of Physics and Information Technology,Shaanxi Normal University,Xi’an 710119,China
Keywords: ultrafast dynamics,high pressure,phase transition,Mott insulator
1.Introduction
The ultrafast dynamics of non-equilibrium excited states offer direct insight into phase transitions in strongly correlated[1–5]and spin–orbit coupling(SOC)materials,[6–10]both of which are key topics in condensed matter physics.In 5d transition metal compounds,particularly typical Mott insulator Srn+1IrnO3n+1(n=1, 2, ∞), electron–electron correlation and spin–orbit coupling have similar energy scales.They play important roles among all cooperative and strong competing interactions resulting in a remarkable playground for exploring not only novel phases at equilibrium states,[11]but also emergent transient phases and ultrafast dynamics of quasiparticles in non-equilibrium processes.[12]Srn+1IrnO3n+1(n=1,2, ∞) has attracted much attention due to complex magnetic states at high critical temperature and abnormal insulating states rather than metallic states.[13–17]This narrow-bandgap Mott insulating phase has a complex lattice frustration under high pressure,[18–20]and does not exhibit the expected insulating state collapse and metallization with compression of the unit cell,which has stimulated great interest in tuning the material with pressure.[19–26]However,the ultrafast dynamics of the transient phases in the non-equilibrium region is still less explored at high pressure,[27,28]especially the related research on Sr3Ir2O7has not been published yet.
Recently, several studies have shown that the magnetic and structural transitions of Sr3Ir2O7at high pressure are interdependent.While at 14 GPa in Sr3Ir2O7,a magnetic transition occurs at 10 K[20]and a structure transition occurs around 25 K,[29]respectively.Because these two transitions are practically simultaneous, it becomes uncertain whether the magnetic transition is caused by the structural transition or vice versa.According to theoretical modeling,[30]the magnetic transition is triggered by a lattice distortion from a tetragonal IrO6octahedral to a cubic IrO6octahedral through spin–lattice coupling.To confirm the prediction requests to decouple the magnetic transition and structural transition.One approach is to investigate the lattice distortion above the N′eel temperature (285 K)[14]where the magnetic transition is inhibited.Intriguingly,such structural transition observable at room temperature as well as the metal–insulator transition does not occur until 60 GPa,[22,30]possibly because the structure change is too small to be resolved by conventional high-pressure xray diffraction and Raman methods.As ultrafast dynamics are sensitive to subtle non-equilibrium state changes, timeresolved studies provide critical information for studying delicate phase transitions at high pressure.
In this work,we investigate the time-resolved differential reflectivity ΔR/Rof Sr3Ir2O7at room temperature and high pressure by combining the pump–probe approach with diamond anvil cells(DAC).Our work has achieved high pressure of 23.2 GPa andin situenvironment.To minimize the errors caused by removing the sample and DAC from the light path to change and measure the pressure, which is a critical step in the pump–probe transient reflectivity measurements, we and colleagues have developed an on-sitein situsetup.[27,28]We discover that above the N′eel temperature,the density and lifetime of quasiparticles (QPs) fluctuate significantly at the transition pressure 14.3 GPa and remain stable in other pressure ranges,indicating the formation of a critical phenomenon.Furthermore, we provide a model that combines quantum interference to account for the crucial behavior near the transition pressure, which provides important information for understanding the phase transition.Our findings suggest that ultrafast non-equilibrium excited states could provide important information for studying phase transitions inaccessible from equilibrium states, and also reveal the potential development prospects for high-pressure ultrafast physics research.
2.Experiments
The 5d transition metal oxide Srn+1IrnO3n+1(n=1,2,∞)with typicalJeff=1/2 Mott insulating state has a tetragonal perovskite structure, wherenrepresents the number of Ir–O layers in each unit cell.Electron hopping depends on the overlapping d–d orbitals of Ir ions or/and the p orbitals of oxygen atom, therefore the ground state is exceptionally sensitive to the lattice structure.Asnincreases,the ground state has narrower charge gapΔand widerJeff=1/2 bandwidth,developing from stable insulating phase in Sr2IrO4to weak insulating state in Sr3IrO7.[14]Sr3IrO7is at the Mott insulation limit with a charge gap of 0.15 eV[31]and a bandwidth of 0.56 eV.[32]The IrO6octahedra in Sr3IrO7has structural distortion with significance for ground state,exhibiting a rotation angle of 11°along thec-axis and a tilt angle of about 1°between thecaxis and thezdirection(Fig.1(a)).[18,33,34]Related reports of Sr3IrO7show that the crystal structure measured from x-ray diffraction is usually stable atI4/mmm[35]symmetry,but may be reduced toBbca,[18]Bbcb[34]or evenC2/c.[33]due to the structural distortion.In this work, the single crystal samples were all synthesized by flux technique.High-purity SrCO3,IrO2and SrCl2·6H2O powders were mixed in a certain proportion and kept at high temperature (~1500 K) for several hours.The high-purity single crystal of 0.8×0.8×0.3 mm3can be obtained after gradually cooling to room temperature.
We performed the high-pressure time-resolved reflectivity measurements on Sr3IrO7single crystals loaded in Mao–Bell type DAC.The DAC enables a pressurized environment by type-II diamonds with 300μm culet size, and T301 stainless steel gaskets with 30 μm thickness and 150–170 μm diameter.The selected square sample has a width of 40–50μm and a thickness of 10μm.The inert gas neon was used as the pressure transmission medium to achieve a better hydrostatic pressure environment, and the specific pressure was obtained through the ruby fluorescence signal.
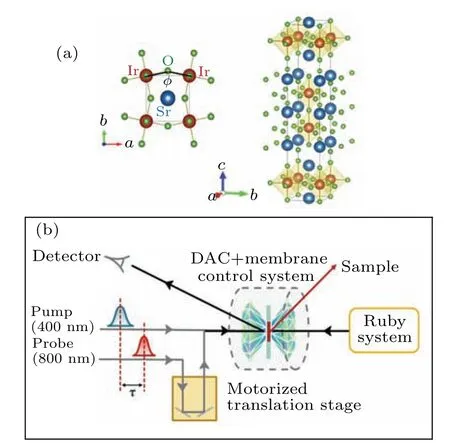
Fig.1.(a)The lattice structure of Sr3Ir2O7,with iridium atoms in red,oxygen atoms in green, and strontium atoms in blue. ? is in-plane rotation angle.(b) The main components of high-pressure pump–probe optical path.
A pump–probe system equipped with a regenerated Ti:sapphire amplifier generates an incident ultrafast pulse laser with a center wavelength of 800 nm,an initial pulse duration of 80 fs,and a repetition rate of 250 kHz.We developed anin situsetup to reduce possible measurement artifacts,[28]in which the DAC pressurized using a gas membrane system was kept fixed in the optical path and the pressure was calibrated with an online spectrometer system.The measurement on Sr3IrO7used a 400 nm pump laser beam with a diameter of 4.93 μm(1/e2beam diameter) and a fluence of 11.89 mJ/cm2, and a 800 nm probe beam with a diameter of 4.69 μm and a fluence of 2.16 mJ/cm2.These beams pass through a motorized translation stage to generate a time-dependent optical path difference,which is time-delayed to enable the time-resolved capacities(Fig.1(b)).The fluences of the pump and probe pulses are linearly dependent on the signal,allowing us to minimize the heating effects.Additionally, the selected data ensures a sufficiently high signal-to-noise ratio, enabling us to acquire high-quality data.
3.Results and discussion
3.1.Time-resolved reflectivity of Sr3Ir2O7 at high pressure
We obtained the dynamic process of Sr3Ir2O7at high pressure of 2–23.2 GPa by time-resolved pump–probe reflectivity(ΔR/R)at room temperature.In the pump–probe experiments,a larger pump laser energy was chosen to enhance the intensity of reflection to counteract the possible drop of the signal passing through the DAC, while the probe energy was concentrated near the Fermi surface we are interested in.According to the electronic structure of Sr3Ir2O7,[22]the 3.1 eV pump laser pulse excites electrons from the O 2p orbital to theJeff=1/2 upper Hubbard band (UHB) in Sr3Ir2O7,[6,36]and the probe laser pulse with an energy of 1.55 eV excites electrons from theJeff=3/2 to theJeff=1/2 states(inset of Fig.2).In theory, ΔR/Ris proportional to the QPs density of the photo-excited states,[37,38]and its variation over time reflects the ultrafast relaxation dynamics observed in pump–probe measurements.ΔR/Rshows a rapid positive peak at the initial time(t=0 ps)and decays with time,as shown in Fig.2.
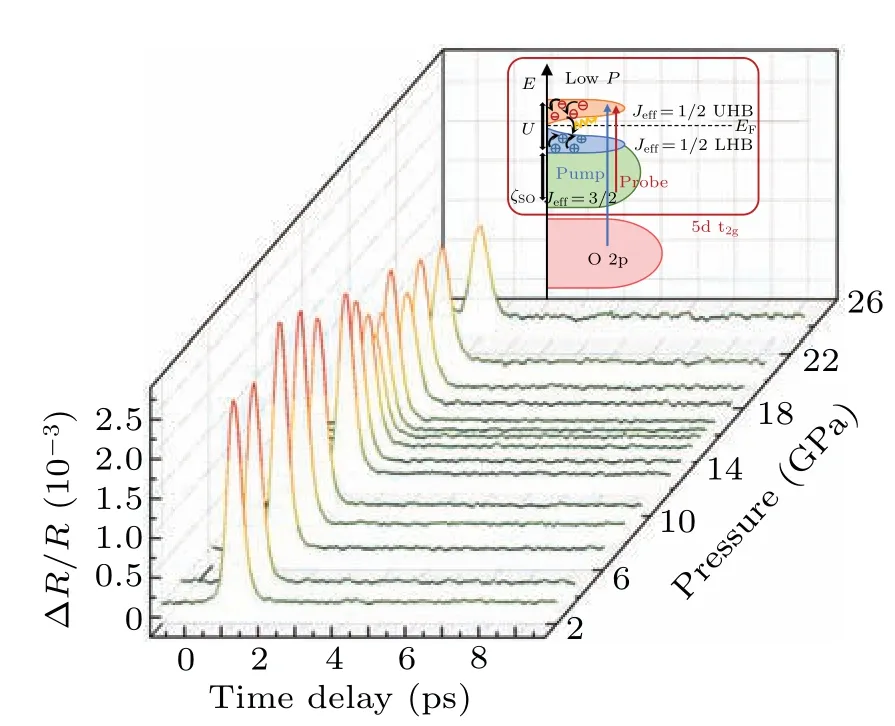
Fig.2.Time-resolved differential reflectivity ΔR/R of Sr3Ir2O7 in the pressure range of 2–23.2 GPa.The colors of the curve (from green to red)show the strength of ΔR/R(from low to high).The inset shows the schematic diagram of the low-energy electronic density of states evolving with pressure.The blue arrow indicates the pump pulse with the energy of 3.1 eV,and the red arrow is the probe pulse with the energy of 1.5 eV.The circles with signs are photo-induced holes and electrons.
Sr3Ir2O7exhibits pressure-regulated rotation and tilt distortions, which can have a significant impact on its magnetic and electrical properties due to the strong influence of O 2p orbitals on electronic hopping.Previous studies have identified a structural phase transition driven by lattice frustration atPc(~14 GPa)using x-ray diffraction(XRD).[29]The antiferromagnetic transition and structural phase transition were found to occur simultaneously atPc,[20]and a several-fold drop in resistivity also occured at this pressure.[30,39]Interestingly,these conclusions were drawn from low-temperature experiments, and neither XRD nor Raman spectroscopy was able to detect the structural transition characteristics at room temperature.The subtle nature of this structural distortion makes it challenging to discern using traditional methods,and its source is difficult to analyze since no symmetry transition is induced.However, despite its subtlety, this transition can cause significant changes in the magnetic and electrical properties,making it a topic of great interest.In our experiments,we have observed that the amplitude of ΔR/Rneart=0 ps decreases with increasing pressure,but exhibits a suppression atPc=14.3 GPa,which is in good agreement with the observed transition pressure.This is the first time that high-pressure phase transition signatures in Sr3Ir2O7have been observed by measuring non-equilibrium dynamics at room temperature.The lattice structure transition also affects the electronic structure,as reflected in the non-equilibrium dynamic process,providing us with a research idea to capture the subtle phase transition.
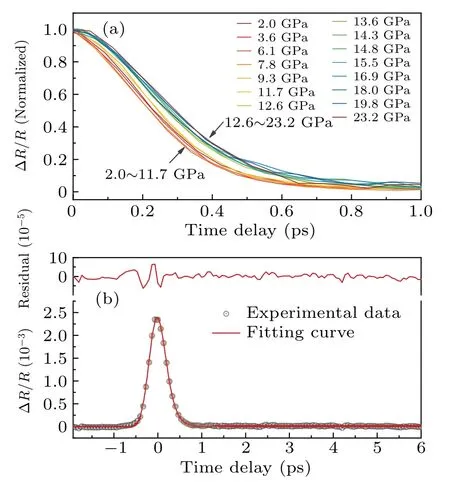
Fig.3.(a) The normalized results of relative differential reflectivity ΔR/R of Sr3Ir2O7.(b)Schematic of the deconvolution fitting of ΔR/R at 9.3 GPa.The red solid curve is the fitting result according to the function.Residuals of fitting are shown by the red line above the experimental data.
Phase transitions can also manifest themselves through relaxation processes ΔR/R(t >0).The dynamic behavior of Sr3Ir2O7occurs quite rapidly(in less than 1 ps),possibly due to its narrow energy band gap.[31]Nevertheless, a comparative analysis of the normalized relaxation process reveals distinct dynamic characteristics within the two pressure ranges(Fig.3(a)).The relaxation process is divided into 2–11.7 GPa and 12.6–23.2 GPa,with the decay becoming slower at higher pressure range.The relaxation frequently involves multiple time-dependent processes, requiring more detailed fitting to determine the details of the phase transitions observed in experiments.Each process can be characterized with two parameters, amplitudeAand lifetimeτ, by fitting ΔR/Rin exponential function.In our measurements, the output signal results from a convolution of the resolution function with the response function from the samples.Peak fitting and deconvolution techniques are commonly used to resolve the time response from samples.Fitting ΔR/Rto the convolution function accomplishes this,[5,9]
where the exponential functionf(t)=Aexp(?t/τ)+A0(A0is the time-independent component) andg(t) is the Gaussian function.The fitted half-width of the Gaussian function is 160 fs, which correlates to the laser pulse.The fitted image and raw data are shown in Fig.3(b), with error bar reflected by the residual that is 1–2 orders smaller than the experimental result (see Appendix B for detailed fitting process).Through deconvolution fitting,the data reflecting the real dynamic process in the experimental results can be more accurately separated,consequently,a clearer and more refined physical image can be extracted.
3.2.Critical anomalies of dynamic parameters at Pc
Sr3Ir2O7usually has two relaxation components at low temperatures.[9]At room temperature, the fitting yields only one process characterized by parametersA,τandA0(Figs.4(a)–4(c)).R, exclusively excited by the probing laser,exhibits a uniform linear relationship (Fig.4(d)), indicating that the critical dynamics reflect sample characteristics rather than being influenced by the background.The linear decrease ofRunder high pressure may be affected by diamond window or pressure transmission medium on pulsed laser under high pressure, and the influence of this problem on the signal can be reduced by ΔR/Rprocessing.We discovered that the densityAand lifetimeτof quasiparticles(QPs)vary significantly atPc,indicating an unusual electrodynamic signature.

Fig.4.Pressure dependence of the (a) amplitude A, (b) lifetime τ and (c)constant A0 in Sr3Ir2O7.(d)The experimentally measured R when only the probe laser is used for excitation.It is relatively stable at high pressure and proves that there is indeed a critical fluctuation.The vertical dotted lines mark the phase transition pressure, and the green curves in(a), (b)and red dotted lines in(a),(c),(d)represent the trend guide of points.
Overall,Adecreases linearly with pressure,but there is a noticeable dip near critical pressure and rapidly reaches a minimum atPc.In this pressure range,τrapidly increases from 0.15 ps to 0.22 ps, also forming a small peak at 14.3 GPa.This type of fluctuation distinguishes a crucial phenomenon from the rest of the pressure range.According to the pressure dependence ofAandτ, the phase space can be divided into three regions: phase I(<Pc),a critical region aroundPc,and phase II(>Pc).Simultaneously,it can be considered that time-independent componentA0fluctuates around a relatively stable constant value at high pressure.The following discussion will focus on the phenomena observed inAandτ.
According to the Fermi gold rule,[40]the amplitudeAin the photoexcited system is dominated by the joint electron density of states between the O 2p band and theJeff=1/2 UHB,and the successive decrease ofAwith pressure reflects the increases in bandwidth due to compression.Given that the O 2p band is commonly wider than theJeff=1/2 UHB, it is expected that the broadening of the O 2p band will play a dominant role in the change ofA, which is not very sensitive to small change of the IrO6octahedral.As pressure-induced increase in bandwidth is common,a decrease in the amplitudeAwith pressure at the non-phase transition point is also frequently observed in some high-pressure studies.[27,41]Another possibility is that the pulse signal is weakened by the diamond window and the pressure medium at high pressure.However,none of the above can explain the problem of fluctuations in the critical pressure pointPcobserved inA.
The fast decay component (as shown in Fig.4(b))less than 1 ps is widely thought to reflect electron–phonon scattering,[27,28]which is usually difficult to change by external temperature or pressure modulation,and also generally manifested a constant in ultrafast experiments.[42]Theτobtained in this experiment remains stable in phases I and II,but exhibits some critical pressure dependence,such as a rapid rise near thePc.
The anomalies observed in the ultrafast dynamics have important implications for the study of difficult-to-metallize properties and associated phase transitions at high pressures.First-principles calculations[30]predict that the 0.15 eV band gap in Sr3Ir2O7will be closed at 20 GPa due to volumereduction-induced bandwidth broadening,[30,39]while up to 60 GPa,Sr3Ir2O7still does not exhibit full metallization.[22,30]This is due to Sr3Ir2O7’s remarkable lattice frustration,which is caused by the spin–orbital coupling presenting in the interplay of the lattice, orbital, spin, and charge.[14,20,22,29,43,44]In previous work, structural phase transitions at~14 GPa were often accompanied by changes in conductivity and magnetism,[20,29,39]and such strong correlations could not be separated.However, the critical anomaly observed in this study coincides well with the phase transition pressurePcand occurs at room temperature (above the N′eel temperature 285 K of paramagnetic–antiferromagnetic transition point),which can clearly rule out the influence of the magnetic order phase transition.Therefore,the observed rapid increase in the quasiparticle(QP)lifetimeτatPccan be attributed to the abundance of lattice distortions in iridium oxides.Theoretical models suggest that high pressure may induce lattice distortion from tetragonal IrO6octahedra to cubic IrO6octahedra,[30]and some experiments have found that variations in the rotational angles within the Ir–O–Ir plane[20]or the tilting angles outside the plane[45]may affect the band structure.These lattice distortions of IrO6octahedra will affect the distribution of O 2p orbitals and overlap of d–d orbitals,[14]leading to hybridization of t2gorbitals and affecting electron hopping,which can result in changes in electron–phonon interaction and/or band gap, and reflected in the dynamic lifetimeτ.In any case, it is obvious that we observed an anomaly in the nonequilibrium dynamics at phase transition pressure through the analysis of the QPs density and lifetime.
3.3.Critical phenomena model
The fluctuations in densityAand lifetimeτaroundPccan also be explained by critical phenomena.The non-equilibrium critical slowing is universally observed at the charge density wave or superconducting transition temperature,[46]however,similar fluctuations near the critical points of other phase transition mechanisms repeatedly found in ultrafast experiments are still poorly understood.[1,27,41,47]In the following section,we use a model to account for the universal temporal behavior of the photoexcited states forming around the phase transition point of the phase transition.
According to Landau phase-transition theory based on the free energy of equilibrium ground states,the well-known critical slowing down or the lifetime divergence under perturbation can clearly be observed at a continuous phase transition point.However,the photoexcited states are far from the equilibrium states and our experiment’s relaxation-time enhancement is relatively weak.More remarkably, in some other experiments,the relaxation time even is strongly shortened at the phase transition point,[3,27]in contrary to the expectation of the critical slowing down.In addition,the density of the photoinduced QPs shows a dip near the critical pressure but almost linearly depends on the pressure in other pressure regimes.A parameter change that is induced by the phase transition is supposed to give rise to a step function-like response for the density.Therefore, a new model is expected to explain the anomaly around the phase-transition point.The anomalous phenomenology of dynamics near a phase transition point is much more general in first and second order phase transitions,glasses and dynamical systems.[48]Here, we propose a phenomenological model to study the time evolution of the photoexcited states near the phase-transition points, as shown in Fig.5.We assume thatψ1andψ2are the wave functions of the excited states in the neighboring phases I or II, respectively.At the phase-transition point,two excited states coexist and weakly couple.The quantum coherence is set up by“tunneling”between the two excited states.Mimicking Feynman’s phenomenological model of the Josephson junction,[49,50]the time evolutions of the two coupling wave functions of the excited states are written as
whereU1,U2andΓ1,Γ2are the energies and the relaxation rates of the two excited states, respectively.KandK'are the state coupling constant and relaxation rate constant, respectively.IfKandK'are zero, then the two Schr¨odinger equations only describe the two respective excited states.Near the phase transition point,the coupling or fluctuation between the two states may induce tunneling from one state to the other.Following Feynman’s method, we define the wave functions aswhereθ1andθ2are the phases of the two wave functions, respectively, andρ1andρ2the corresponding densities of the QPs of the two excited states.Substituting the above equations into the Schr¨odinger equations,one gets
with the phase differenceδ=θ2?θ1.We further define the total excited QPs density asρ=ρ1+ρ2, givingˉh?ρ/?t=?2Γ'ρwith the effective relaxation rate
We assumeΓ1≈Γ2=Γwhen only considering the phasetransition point;then,the effective relaxation rate reads

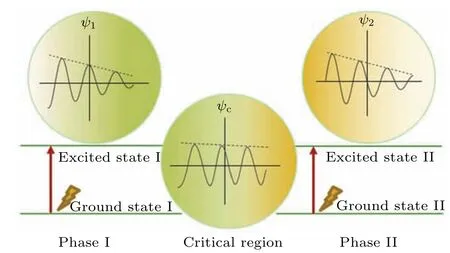
Fig.5.Schematic of critical point model demonstrating interference between two excited states belonging to two neighboring phases.The wave figures show the real (imaginary) part of the wave functions ψ1 =?1 eiθ1 in phase I, ψ2 =2 eiθ2 in phase II and ψc in the critical region.The ground state I, II and the excited state I, II could coexist together and the relaxation time could be far from that in phase I and II in the critical region.
4.Conclusion and perspectives
In summary, we investigated the ultrafast dynamics in photo-excited Sr3Ir2O7under high pressures at 300 K by applyingin situtime-resolved differential spectroscopy.The density and lifetime of QPs vary widely atPc=14.3 GPa, evincing the lattice phase transition induces significant changes in the transient dynamics.Furthermore, we propose a model that accounts for the crucial behavior near the transition pressure point.The ability to reveal novel phase from its distinct non-equilibrium states demonstrated in this study gives a new way to investigate more delicate phases at high pressure, which are unresolvable by standard x-ray diffraction and Raman spectroscopy.Since non-equilibrium dynamics involves many influencing factors, we need further experimental or computational support to explain the observed physical phenomena at high pressure clearly.For example,if the correlation between structural transformation and electroacoustic coupling can be clarified, the lifetime difference between two phases at high pressure can be well explained by electron–phonon coupling alone without introducing other considerations.In any case,paying attention to nonequilibrium state under high pressure will provide a new perspective for the study of condensed matter physics and help people solve some long-standing problems.
Appendix A: The trajectories of Gaussian function and exponential function fittings
In the measurements,the output signal is resulted from a convolution of the temporal resolution function of the instrument with the temporal response function from the materials.To resolve the time response from samples, one needs to apply peak fitting and deconvolution techniques,the precision of such analysis is typically about 1/10 of the temporal resolution of the experiment, which in this study is about 8–10 fs.Figure A1 shows the analysis.It can be observed that using deconvolution fitting reveals the true relaxation dynamics process(green curve),while neglecting this treatment would mask this information.
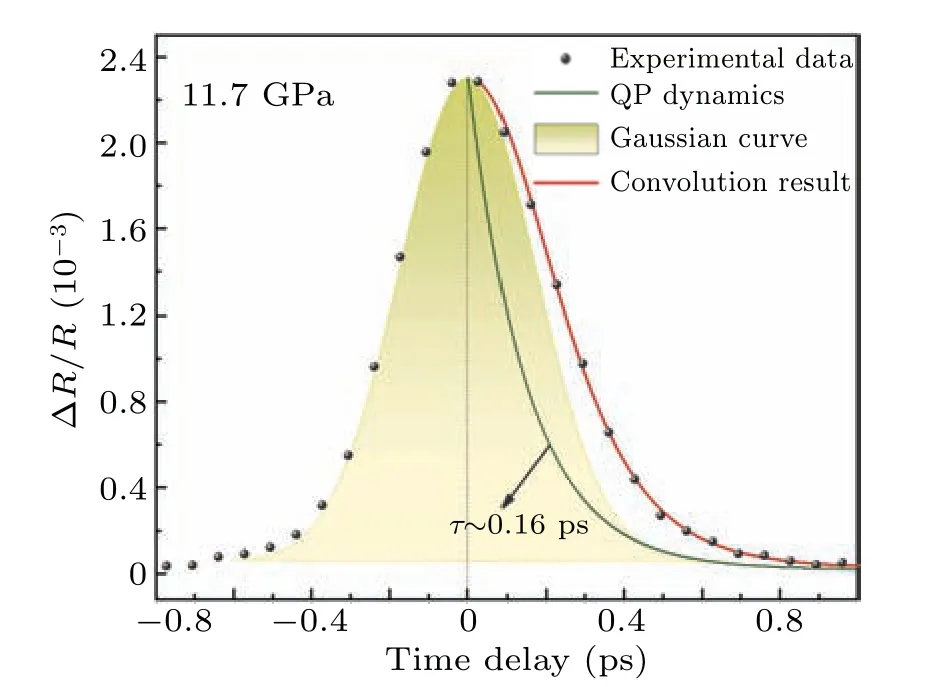
Fig.A1.Deconvolution of the QP dynamics in Sr3Ir2O7.
Appendix B: Deconvolution fitting of high pressure time-resolved dynamics
In this study, carefully fitting the dynamic spectra under high pressure was performed,as shown in the comparison between the deconvolution fitting results and the original data of the differential reflectivity ΔR/R.The peak shape of the differential reflectivity can be well fitted, and the relaxation parameters obtained from the fitting above 0 ps accurately reflect the dynamic processes of the experimental data.

Fig.B1.Raw data and deconvolution fitting results of each highpressure ultrafast dynamic spectrum in the pressure range of 2–23.5 GPa.
Acknowledgements
The project supported by the National Key Research and Development Program of China (Grant No.2018YFA0305703), Science Challenge Project (Grant No.TZ2016001), and the National Natural Science Foundation of China(Grant Nos.U1930401 and 11874075).
- Chinese Physics B的其它文章
- Photophysics of metal-organic frameworks: A brief overview
- Anelasticity to plasticity transition in a model two-dimensional amorphous solid
- Ab initio nonadiabatic molecular dynamics study on spin–orbit coupling induced spin dynamics in ferromagnetic metals
- Universal basis underlying temperature,pressure and size induced dynamical evolution in metallic glass-forming liquids
- Valley filtering and valley-polarized collective modes in bulk graphene monolayers
- Sharing quantum nonlocality in the noisy scenario

