Anelasticity to plasticity transition in a model two-dimensional amorphous solid
Baoshuang Shang(尚寶雙)
Songshan Lake Materials Laboratory,Dongguan 523808,China
Keywords: amorphous solid,deformation mechanism,anelasticity to plasticity transition,molecular dynamics simulation
1.Introduction
Amorphous solids, as non-equilibrium materials, have captivated the interest of both academic researchers and industrial applications due to their diverse deformation behaviors.[1–3]However, unlike crystalline materials, the underlying deformation mechanism in amorphous solids remains a topic of debate.While crystalline materials exhibit topological defects such as dislocations or grain boundaries as plasticity carriers,amorphous solids rely on shear transformations or rearrangement events rather than specific topological structures.[4–6]
Previous studies[7–11]have observed that rearrangement events in amorphous solids are localized and can occur within the apparent elastic regime.However,considering plastic rearrangements as excitation elements is inappropriate due to their entanglement with long-range elastic interactions and plastic events.[12–18]Consequently,identifying the excitation element in amorphous solids remains a topic of ongoing debate.[5,19]
Furthermore, it is crucial to note that not all rearrangement events in amorphous solids exhibit irreversible plastic behavior.Recently, a new type of rearrangement event characterized by an intrinsic anelastic nature has garnered significant attention.[20–23]Unlike plastic events, these anelastic rearrangements are reversible during the loading–unloading process.They play a vital role in influencing various mechanical properties of amorphous solids,including relaxation,[24,25]thermal cycling rejuvenation,[26]mechanical anisotropy,[27,28]and memory effect.[29,30]
However,the understanding of the discrepancies and connections between anelastic and plastic events, as well as the key parameters governing the transition from anelasticity to plasticity, remains elusive.Further investigations are necessary to unravel the underlying mechanisms and establish a comprehensive understanding of the relationship between these two deformation modes in amorphous solids.
In this study, we aim to address these questions through molecular dynamics simulations.We investigate the mechanical response of amorphous solids using athermal quasistatic shear and frozen matrix methods.Our focus is on observing the transition from anelasticity to plasticity and understanding the underlying mechanisms.By analyzing the characterized parameters,we identify three distinct deformation modes:elasticity,anelasticity,and plasticity.Specifically,we explore the effects of finite system size on these parameters.Our findings reveal that anelasticity precedes plasticity and serves as a critical intermediary between elasticity and plasticity.Furthermore,we observe that anelastic events,characterized by their system size independence, exhibit a localized nature within the material.On the other hand,plastic events display subextensive behavior.This suggests that plasticity emerges from the collective interaction of a series of anelastic events.As a result, anelastic events can be regarded as potential element excitations in amorphous solids.
2.Method
2.1.Initial sample preparation
We used a well studied two-dimensional binary Lenard–Jones model with a polynomial cutoff smooth[21,31]to investigate the mechanical property of amorphous solid.All units were expressed in terms of the massmand the two parameters describing the energy and length scales of interspecies interaction,εandσ,and the Boltzmann constantkB=1.Therefore,the time was measured in units ofand the temperature was measured in units ofT0=ε/kB.The composition ratio of large(L)and small(S)wasNL:100 samples each containing 104atoms with periodic boundary condition were obtained by quenching fromT=2.0 toT=0.18 with constant volume,and the quench rate was fixed at 0.0000325T0/t0, and then the initial sample was obtained by minimized the quenched sample with conjugate gradient(CG)method,where the fictive temperature of the sample was around 0.335.The reduced density of system was fixed at 1.02.All the results were presented in reduced units.We performed all the simulations using the LAMMPS molecular dynamics package,[32]and used the OVITO package[35]for atomic visualization.
2.2.Frozen matrix method
Frozen matrix method is a useful tool to investigate the local yield stress[34]or local modulus[35]of the amorphous system,and local relaxation time[17]of supercooled liquid,it can also use to study the thermally activated rearrangement[36]and to calibrate more quantitatively elastoplastic models,[37]even for different preparation protocols.[38]Here,we extended this method to study the anelasticity to plasticity transition in the amorphous solid.The investigated region was selected within a radiusR, then the outside region was frozen with affine deformation(Fig.1(a)).In this study,the investigated region was fixed at the center of each sample.The mechanical response of amorphous solid was probed by the athermal quasi-static shear(AQS)protocol.The simple shear deformation was performed in all regions and the shear strain increment wasδγ=10?5,during each shear strain increment,the investigated region was relaxed by energy minimization, and the outside region was frozen with affine deformation.The loading process continued until the shear strain reached 0.3.The choice of 0.3 was not grounded in specific physical reasoning;rather,it was selected to ensure that all investigated samples exhibited a transition from anelasticity to plasticity.

Fig.1.The loading process of the amorphous solid.(a)The schematic of frozen matrix deformation.(b)The shear stress τ changes with shear strain γ in various systems.(c) The potential energy U ?UI changes with strain in various systems.(d) The typical stress drops in R=26 system and the corresponding atomic displacement color map shown in the inset.(e)The stress drops(Δτ)changes with strain in R=5 and R=26 systems.(f)The potential energy drop(ΔU)changes with strain in R=5 and R=26 systems,respectively.
2.3.Physical property characterization
2.3.1.Anelastic event and plastic event
During the loading process, stress and potential energy drops occur (Figs.1(b) and 1(c)), which are caused by rearrangement events (Fig.1(d)).A rearrangement event is defined as when the maximum atomic displacement exceeds 0.1,or the potential energy drop per atom ΔUis greater than 0.1,in the investigated region.To characterize the anelastic and plastic events, the following unloading process was performed.After each potential energy drop,the shear strain was reversed and sheared back toγ=0,which is called the unloaded sample.The mean squared displacement(MSD)between the unloaded sample and the initial sample was compared, and if MSD was zero,the drop was an anelastic event; otherwise,it was a plastic event.The potential energy per atomUand the shear stressτof the investigated region were monitored during the loading and unloading processes, and the shear strain increment was fixed atδγ=10?5.
2.3.2.Atomic displacement
To compare configuration 1 and configuration 2, the atomic displacement of atomiis defined asdi=ri(1)?ri(2),whereri(1)is the coordination vector of atomiciat configuration 1.The MSD between two configurations can be defined as 1/N∑i∈N di·di,whereNis the atomic number in the investigation region.
3.Results and discussion
Figure 1 shows the loading process of the amorphous solid with various system sizes.There are notable finite size effects with frozen matrix boundary condition, both the frequency of stress drop Δτand potential energy drop per atom ΔUincrease with system sizeR.Conversely, the amplitudes of Δτand ΔUdecrease with the system size (Figs.1(e) and 1(f)).During the stress drop (Fig.1(e)), the atomic displacementdishows a typical quadrupolar symmetry.This is qualitatively consistent with the situation with periodic boundary condition.[10,39]However, the frozen matrix boundary condition not only blocks the long range elastic interaction from outside region,but also causes significant confinement effect.[17]As suggested by Regevet al.,[23]the confinement effect can lead to reversible rearrangement.As shown in Fig.2, forR=6 system, both the stress and potential energy state are fully recovered after the loading–unloading process, indicating an anelastic behavior.In contrast, forR= 26 system,both the stress and potential energy states are different from the initial ones, indicating a plastic behavior.Interestingly,forR=11 system,the stress state is almost recovered but the energy state is not.This behavior can be attributed to the confinement effect of the frozen matrix boundary,and it signifies a transition from anelasticity to plasticity controlled by the system size.Increasing the system size weakens the confinement effect, thereby influencing the nature of the deformation response.
Moreover,it should be noted that for a given system size,the increase in strain can also lead to a transition from anelasticity to plasticity.This behavior is depicted in Fig.3,which illustrates the loading process with various unloading processes for a system size ofR=11.When the unloading process starts from a strain ofγ=0.14, the potential energy of the system can be fully recovered to its initial state.However, when the unloading process starts fromγ=0.15 orγ=0.19, the potential energy of the unloaded samples(back-1 and back-2)is higher than that of the initial state (Fig.3(a)).The loading process exhibits a characteristic first drop strain, denoted asγe=0.02545(Fig.3(b)).When the loading strainγis smaller thanγe,the loading–unloading process can be fully recovered.This behavior is indicative of elasticity, where no dissipation(∮τdγ ≡0)occurs during the loading phase.
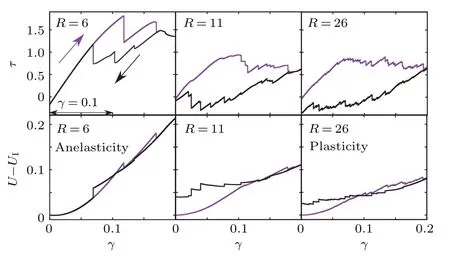
Fig.2.The loading and unloading process for various system sizes.The up panel shows the shear stress evolves with shear strain during loading and unloading processes,the down panel shows the potential energy evolves with shear strain.The purple arrow and black arrow illustrate the loading and unloading directions,respectively.
In addition, when the loading strain exceedsγe(γ >γe),the potential energy–strain curve exhibits sudden drops, indicating atomic rearrangement events.These energy drops are further examined through the unloading process.The last energy drop corresponding to an anelastic event can be identified (Fig.3(c)).The loading process exhibits a last anelastic drop strain denoted asγp=0.145.For loading strains betweenγeandγp, the loading–unloading process can be fully recovered,but dissipation occurs.When the loading strain exceedsγp(γ >γp), the unloaded sample cannot be fully recovered to its initial state, and plastic rearrangement takes place.The displacement color map of the anelastic drop is presented in Fig.3(d).A comparison of the atomic displacement during the anelastic drop with the plastic displacement of back-1 and back-2 samples reveals that the atomic displacement during the anelastic drop is reversible,while plastic rearrangement results in permanent displacement.By comparing the energy of the unloaded sample with that of the initial state,three types of mechanical properties during the loading process can be identified: elasticity,anelasticity,and plasticity(Fig.3(e)).
The anelasticity to plasticity transition is both controlled by system sizeRand loading strainγ, and the key parameters for the transition areγeandγp.Figure 4(a) shows that the mean values ofγeandγpdecrease with system sizeR,and the finite size effect can be well depicted by a power-law formulaγ~R?α, i.e.,γe~R?1.09±0.02andγp~R?0.86±0.04.The discrepancy of exponent betweenγeandγpreveals that,as the system size increases,the anelastic property will be more significant.It will dominate the deformation of the apparent elastic region.Furthermore,for thermodynamic limitR →∞,both elasticity and anelasticity will disappear,and the intrinsic mechanical property of amorphous solid is inelasticity,this is consistent with the observation of avalanche statistics in the apparent elastic region.[17]It confirms that regardless of the boundary condition, the nature of amorphous solid is inelastic.
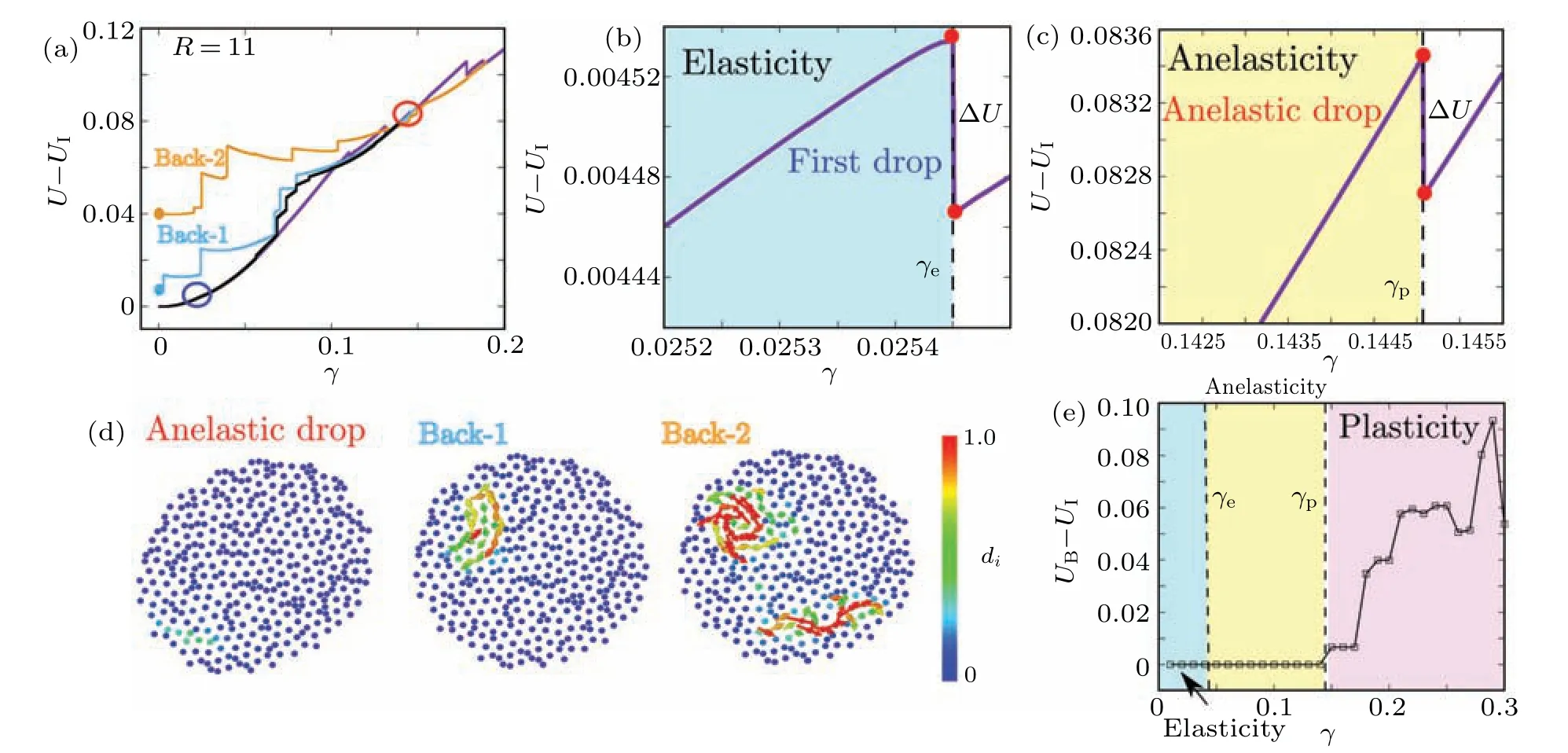
Fig.3.The characterization of elastic, anelastic and plastic events by loading–unloading process.(a) The potential energy per atom (U) changes with strain during loading and unloading processes,where UI is the potential energy per atom of the initial state.The purple curve shows the loading process, and the black one shows the anelastic unloading process, starting from a strain of γ =0.14.The yellow and cyan unloading curves start from γ =0.15 and 0.19,respectively,and back-1 and back-2 indicate the corresponding unloaded states.(b)The first drop event during the loading process, marked by a blue circle in (a), and the strain of the first drop event (γe), below which the unloading curve matches the loading curve.(c)The last anelastic drop event during the loading process,and the corresponding strain(γp),marked by a red circle in(a).(d)Depiction of atomic displacement in three sample scenarios: anelastic drops,back-1,and back-2.(e)Evolution of potential energy difference from the unloaded state to the initial state with loading strain.Three distinct regions are illustrated by γe and γp,indicated by the vertical dash line.

Fig.4.(a) The strain boundaries of elasticity and anelasticity γe and of anelasticity and plasticity γp depend on system size R.(b)The mean value of avalanche size NΔU for anelasticity and plasticity,respectively,varies with the square of the system size R2.
The finite size exponent can determine the property of avalanche statistic,and the avalanche size is defined asNΔU.The boundary between anelasticity and plasticity is marked byγp.Avalanches during loading betweenγeandγpare anelastic;beyond this range,they are plastic.Figure 4(b)illustrates avalanche size statistics.Plastic avalanches grow with the system size, while anelastic ones stay constant regardless of the size.It reveals that the anelastic avalanche is a localized event,which is distinguished from the sub-extensitive nature of plastic avalanche.[12,13]The anelastic event can be recognized as the basin hopping within a metabasin based on the view of potential energy landscape,[24,40]and the accumulation of basin hopping would arouse metabasin hopping, it means that the plastic event can be only triggered when the strain is larger thanγp.Therefore,the anelasticity can be identified as the activation of element excitation,such as STZ[10]or fluid units,[41]and the sub-extensitive plasticity is composed of the element excitation,and entangled with long range elasticity.
4.Conclusion
In summary, our study focused on understanding the transition from anelasticity to plasticity in amorphous solids.We employed molecular dynamics simulations using athermal quasistatic shear and frozen matrix methods.By analyzing various parameters, we identified three distinct deformation modes: elasticity, anelasticity, and plasticity.We found that anelasticity acts as a critical intermediary between elasticity and plasticity,and it precedes the onset of plastic deformation.The transition from anelasticity to plasticity is influenced by both the system size(R)and the applied loading strain(γ).We characterized this transition using key parametersγeandγp.The transition from anelasticity to plasticity occurs when the loading strain exceedsγp.Anelastic events were found to exhibit localized behavior,while plastic events exhibited subextensive behavior.
Our findings suggest that plasticity arises from the interaction of a series of anelastic events,with anelastic events acting as potential element excitations in amorphous solids.The transition from anelasticity to plasticity is influenced by system size and loading strain, and the properties of avalanche statistics depend on the system size and the distinction between anelastic and plastic avalanches.
Acknowledgements
Project supported by Guangdong Major Project of Basic and Applied Basic Research, China (Grant No.2019B030302010), the National Natural Science Foundation of China (Grant No.52130108), Guangdong Basic and Applied Basic Research, China (Grant No.2021B1515140005), and Pearl River Talent Recruitment Program(Grant No.2021QN02C04).
- Chinese Physics B的其它文章
- High responsivity photodetectors based on graphene/WSe2 heterostructure by photogating effect
- Progress and realization platforms of dynamic topological photonics
- Shape and diffusion instabilities of two non-spherical gas bubbles under ultrasonic conditions
- Stacking-dependent exchange bias in two-dimensional ferromagnetic/antiferromagnetic bilayers
- Controllable high Curie temperature through 5d transition metal atom doping in CrI3
- Tunable dispersion relations manipulated by strain in skyrmion-based magnonic crystals

