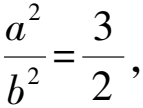
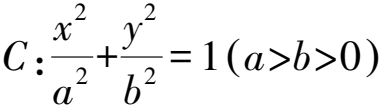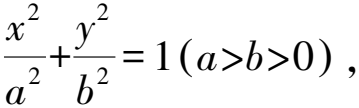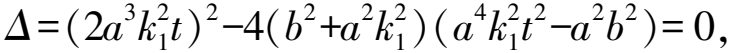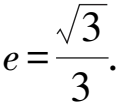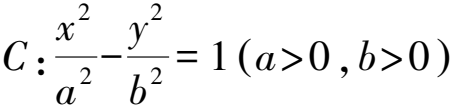圓錐曲線離心率的求解策略
李發(fā)明
(山東省泰安第一中學,山東 泰安 271000)

1 直接分析圓錐曲線的扁平程度
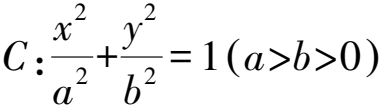
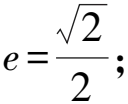


評注橢圓的離心率e∈(0,1),離心率越小橢圓越圓,離心率越大橢圓越扁.雙曲線的離心率e∈(1,+∞),離心率越小張口越小,離心率越大張口越大.直接分析圓錐曲線的扁平程度有時能起到立竿見影的效果.
2 由幾何關系構造等式求離心率

解析設|PF2|=x,則|PF1|=3x.

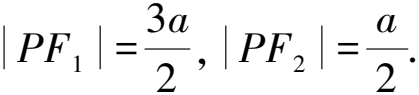
由余弦定理,得
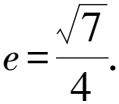


評注充分挖掘題干中所包含的信息,尋找合適的幾何關系,建立關于a,b,c的等式,求出離心率.
3 由幾何關系構造不等式求離心率

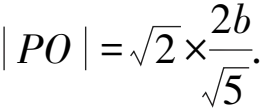
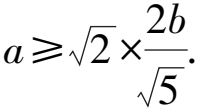

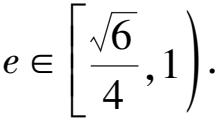
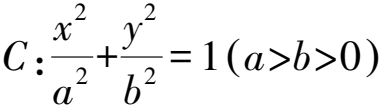
解析連接AF1,BF1,則A,F1,B,F四點構成平行四邊形,設|FB|=x,則|FA|=2x,|AF1|=x.
所以x+2x=2a.



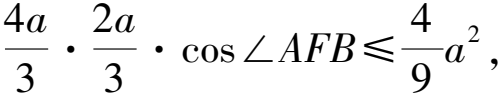
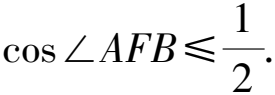
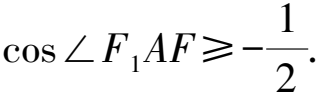


評注利用題干中包含的幾何關系,建立關于a,b,c的不等式,求出離心率的取值范圍.
4 解齊次方程(或齊次不等式)求離心率
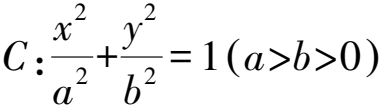
解析AP的垂直平分線過點F等價于在橢圓上存在點P使得|PF|=|AF|.
整理,得ac+2c2-a2≥0.
左右兩邊同時除以a2,得2e2+e-1≥0.

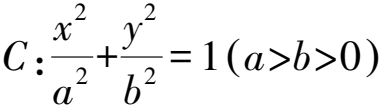


因為焦點F在正方形ABCD的外面,

即c2(a2+b2)>a2b2.
即c4-3a2c2+a4<0.
左右兩邊同時除以a4,得e4-3e2+1<0.
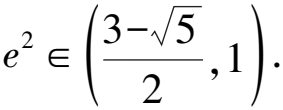
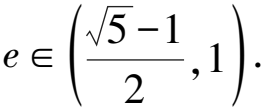
評注利用題干中包含的幾何關系,建立關于a,b,c的等式(或不等式)之后,有時會得到一個關于a,c的齊次式,此時只需將等式(或不等式)兩邊分別除以a或a2或a4轉化為關于e的方程(或不等式),解方程(或不等式)即可得e(或e的取值范圍).解齊次方程(或齊次不等式)求離心率在高考及模擬考試中考查最頻繁,地位最重要.
5 利用橢圓的參數(shù)方程求離心率
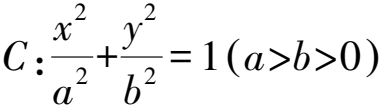
解析設P(acosφ,bsinφ),易知B(0,b).

即a2cos2φ+b2sin2φ-2b2sinφ+b2≤4b2.
即c2sin2φ+2b2sinφ+3b2-a2≥0.
令t=sinφ,t∈[-1,1],則c2t2+2b2t+3b2-a2≥0對t∈[-1,1]恒成立.


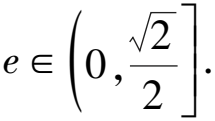

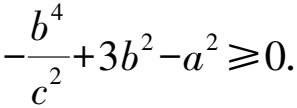
即-b4+2b2c2-c4≥0.
即-(b2-c2)2≥0,此時b=c,與b 所以a2cos2φ-c2+b2sin2φ≤ac對任意實數(shù)φ恒成立. 即c2cos2φ-c2+b2≤ac. 左右兩邊同時除以a2,得e2+e-1≥0, 解析題干所述符合橢圓的第三定義, 評注圓錐曲線的第三定義:平面內的動點到兩定點A1(-a,0),A2(a,0)的斜率乘積等于常數(shù)e2-1的點的軌跡叫做橢圓或雙曲線(實際上兩定點關于原點O對稱即可),當e∈(0,1)時軌跡為橢圓,當e∈(1,+∞)時軌跡為雙曲線.利用圓錐曲線的第三定義求離心率在近幾年的高考模擬考試中頻繁出現(xiàn),應引起足夠重視. 故選ACD. 由余弦定理,得(2c)2=(a1+a2)2+(a1-a2)2-2(a1+a2)(a1-a2)cos60°. 兩式相減,得 因為M(-3,2)為線段AB的中點, 所以x1+x2=-6,y1+y2=4. 所以切線AC的方程為y=k1(x+at). 切線BD的方程為y-bt=k2x. 解析不妨設點A在第一象限,記△AF1F2的內切圓的圓心為點M,圓M與x軸切于點N,由三角形內心的性質我們有 所以點N的橫坐標為a. 所以點M的橫坐標為a. 因為AF2與漸近線平行, 整理,得3c2-8ac+5a2=0. 所以3e2-8e+5=0, 評注求圓錐曲線的離心率(或離心率的取值范圍)是高考的重點也是熱點,問題的關鍵在于通過題干中的條件,尋找a,b,c所滿足的幾何關系,有時是等量關系,有時是不等關系,列出幾何關系之后往往還需要消去b2,轉化為關于a,c的等式(或不等式),進而求解.例15是典型的弦的中點問題,點差法是處理這類問題的利器;例16是具有相同離心率的橢圓方程的設法;例17與三角形內心的性質有關,這些特殊問題的特殊解法也是需要掌握的.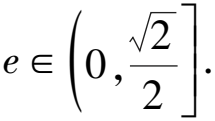
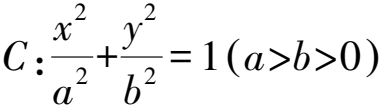


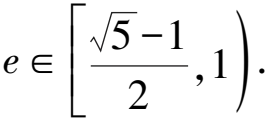
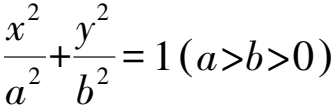
6 利用圓錐曲線的第三定義求離心率
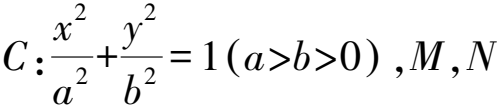
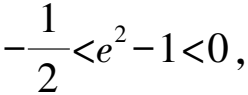
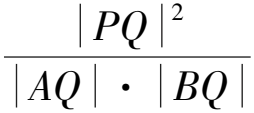


7 橢圓與雙曲線結合的問題

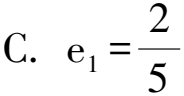
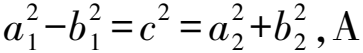
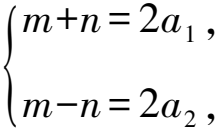


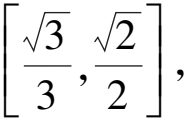

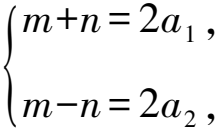
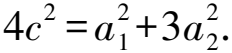

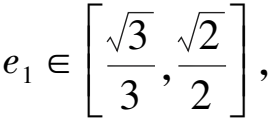
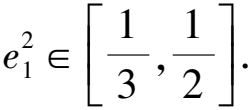
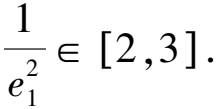
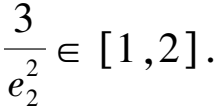

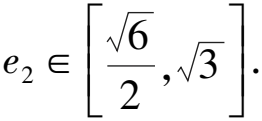
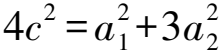
8 求圓錐曲線的離心率雜題賞析