Underwater Acoustic Signal Noise Reduction Based on a Fully Convolutional Encoder-Decoder Neural Network
SONG Yongqiang, CHU Qian,LIU Feng, WANG Tao, and SHEN Tongsheng
Underwater Acoustic Signal Noise Reduction Based on a Fully Convolutional Encoder-Decoder Neural Network
SONG Yongqiang1), 2), CHU Qian3),LIU Feng1), *, WANG Tao1), and SHEN Tongsheng1)
1),100089,2),100071,3),264000,
Noise reduction analysis of signals is essential for modern underwater acoustic detection systems. The traditional noise reduction techniques gradually lose efficacy because the target signal is masked by biological and natural noise in the marine environment. The feature extraction method combining time-frequency spectrograms and deep learning can effectively achieve the separation of noise and target signals. A fully convolutional encoder-decoder neural network (FCEDN) is proposed to address the issue of noise reduction in underwater acoustic signals. The time-domain waveform map of underwater acoustic signals is converted into a wavelet low- frequency analysis recording spectrogram during the denoising process to preserve as many underwater acoustic signal characteristics as possible. The FCEDN is built to learn the spectrogram mapping between noise and target signals that can be learned at each time level.The transposed convolution transforms are introduced, which can transform the spectrogram features of the signals into listenable audiofiles. After evaluating the systems on the ShipsEar Dataset, the proposed method can increase SNR and SI-SNR by 10.02 and 9.5dB, re- spectively.
deep learning; convolutional encoder-decoder neural network; wavelet low-frequency analysis recording spectrogram
1 Introduction
The collected signals from underwater targets such as ships and submarines may contain a portion of reverberant noise with complex spectral components due to the interference from complex and variable natural sound sources (Stulov and Kartofelev, 2014; Klaerner, 2019). Thesenoise disturbances can affect the detection, localization, andidentification of underwater acoustic signals. Therefore, help- ing the underwater acoustic signal-to-noise ratio achieve the experimental requirements before processing target source monitoring is necessary.
Underwater acoustic noise reduction methods can be divided into two main categories after a long development period: traditional and artificial intelligence methods. Traditional methods usually involve experimentalists using manual processing to achieve underwater acoustic signal noise reduction, which is essentially a data preprocessing step based on equational inference, relying on a blind source separation framework and interpretable assertions to construct denoising algorithms. Examples of these algorithms include multi-resolution and high-precision decomposition (Huang., 2012), bark wavelet analysis (Wang and Zeng, 2014), energy significance (Taroudakis, 2017),and empirical mode decomposition. However, as the environment changes, the corresponding biological and marine environmental noise will also change, causing significant dynamic deviations in the noise signal source. Chen(2021) showed that multiple feature extraction me- thods have an important impact on processing the original dataset. Thus, the traditional algorithm fails to learn stable noise features, making it difficult to realize breakthroughs in the signal-to-noise ratio after signal processing (Vincent., 2006). Additionally, these experiments can achieve simplified operations and partial assumptions only under certain types, particular circumstances, or partial sequences of signals (Le., 2020). These traditional methods fail to satisfy the extensive and varied nonlinear feature learn- ing capability of underwater acoustic signals.
Deep learning-based models (Hao., 2016) have de-monstrated considerable potential for applications in various disciplines compared to traditional approaches (Wu and Wu, 2022). For example, Wang(2020) proposed a novel stacked convolutional sparse denoising autoencoder model to complete the blind denoising task of underwater heterogeneous information data. Zhou and Yang (2020) de- signed a convolutional denoising autoencoder to obtain de- noising features with multiple images segmented by parallel learning and used it to initialize a parallel classifier. Yang(2021) presented deep convolutional autoencoders to denoise the clicks of the finless porpoise. Russo(2021)proposed a deep network for attitude estimation (DANAE), which works on Kalman filter data integration to reduce noise using an autoencoder. Qiu(2021) presented a reinforcement learning-based underwater acoustic signal processing system. However, complex system design and the selection of critical parameters are required to satisfy the oscillation conditions and maintain the nonlinear system of signal and noise balance. Zhou(2022) introduced the PF3SACO to accelerate convergence, improve search capability, enhance local search capability, and avoidpremature. The generative network is used to create highlyspurious data, and the discriminator is utilized to discriminate data availability. Yao(2022) expected that the scarcity problem of noisy data in complex marine environ-ments could be solved. However, the unstable marine environment makes the experiment costly, considering working time and human resources. Xing(2022) used or- thogonal matching pursuit and the optimal direction me- thod (MOD) to eliminate some noise in the underwater acoustic signal. Reaching a high step is difficult for signal-to-noise ratio improvement despite its adaptive capability. The signal reconstruction is completed in accordance with the updated dictionary and sparse coefficients. These intelligent methods mainly extract signal features manually, which causes a considerable amount of detail to be lost in the original signal (Hinton, 2015; Zhao,2021). However, these methods do not have the batch pro- cessing denoising function for underwater acoustic signals. In addition, numerous problems, such as changes in the ocean environment and the mixing of multichannel signals,increase the difficulty of obtaining high-quality signals for the above methods. Thus, realizing a breakthrough in the signal-to-noise ratio of the collected underwater acoustic signals is challenging.
Existing mature deep learning methods are difficult to reference and apply directly due to the unique characteris- tics of underwater acoustic signals compared to their acous- tic methods. With the application of the Fourier transform, thetime-domain signal can be converted to the time-frequency domain for representation. Compared with familiar images, the conventional time-frequency spectrum has no specific meaning and lacks texture features. However, somespecific correlations exist between the two axes of the spectrum.
These correlations must be dealt with concurrently du- ring the state analysis, which poses a significant challenge for feature extraction. In addition, traditional feature extraction methods (such as smoothing noise and removing outliers) frequently extract trait values without model training. Indiscriminate processing methods gradually contribute to the loss of some of the detailed information in the feature vector in subsequent module delivery. Therefore, a new low-frequency wavelet analysis of the recorded spectrumand a fully convolutional encoder-decoder neural network is proposed to reduce the noise of underwater acoustic signals. The following three significant contributions are in- cluded in this paper.
1) A new feature extraction technique is proposed to replace the data preprocessing procedure to extract the spectrogram of underwater acoustic signals effectively. This technique combines wavelet decomposition and low- frequency analysis theories to extract features from under- water acoustic signal spectrograms recorded in the time domain as the input of the denoised model.
2) The encoder-decoder framework is constructed to build the deep network. The fully convolutional encoder can compress underwater acoustic feature vectors of different lengths into the high-order nonlinear feature of the same dimension and obtain the optimal expression vector by designing different kernel sizes. More importantly, the transposed convolutional decoder can solve the bottleneck of information loss due to long sequence to fixed-length vector conversion.
3) A mapping-based approach that replaces masking is employed to optimize the fully convolutional encoder-de- coder neural network. The fully convolutional mapping layer is introduced, which contributes to extracting the local characteristics of signals and timing correlation pieces of information without considering the features of the pure natural noise signal.
2 Methodology
An overview of the proposed system is provided, and the following two parts of the pipeline are then analyzed: the wavelet low-frequency analysis recording spectrogramextraction and the fully convolutional encoder-decoder neu- ral network structure.
2.1 System Overview
First, wavelet low-frequency analysis recording spectrum features are extracted to increase the correlation be- tween adjacent frames. Second, a fully convolutional neural network and encoder-decoder network model is used for signal noise reduction, which extracts the structural and local information of the spectrum and considers contextualknowledge of the timing signal. Moreover, a brief description of the method is shown in Fig.1.
2.2 Wavelet Low-Frequency Analysis Recording Spectrogram Extraction
The wavelet low-frequency analysis recording spectrogram can be used to construct a feature map with desired characteristics by modifying different wavelet functions without the required CUDA space. More importantly, the generation of the feature spectrogram is independent of the interval, surface, interval sampling, and signal length. The wavelet low-frequency analysis recording spectrogram extraction is divided into three steps. The first step is to decompose the underwater acoustic signal sequence. The entire decomposition process is shown in Fig.2, and the operation is as follows:
Given an underwater acoustic signal sequence, as shown in Eq. (1), wherexis a value in the sequence, andis a time node:

A partial sequence of sequenceis selected and divided into two parts according to the series of parity samples, as shown in Eqs. (2) and (3), whereXandXare sequences of even and odd segments, respectively:
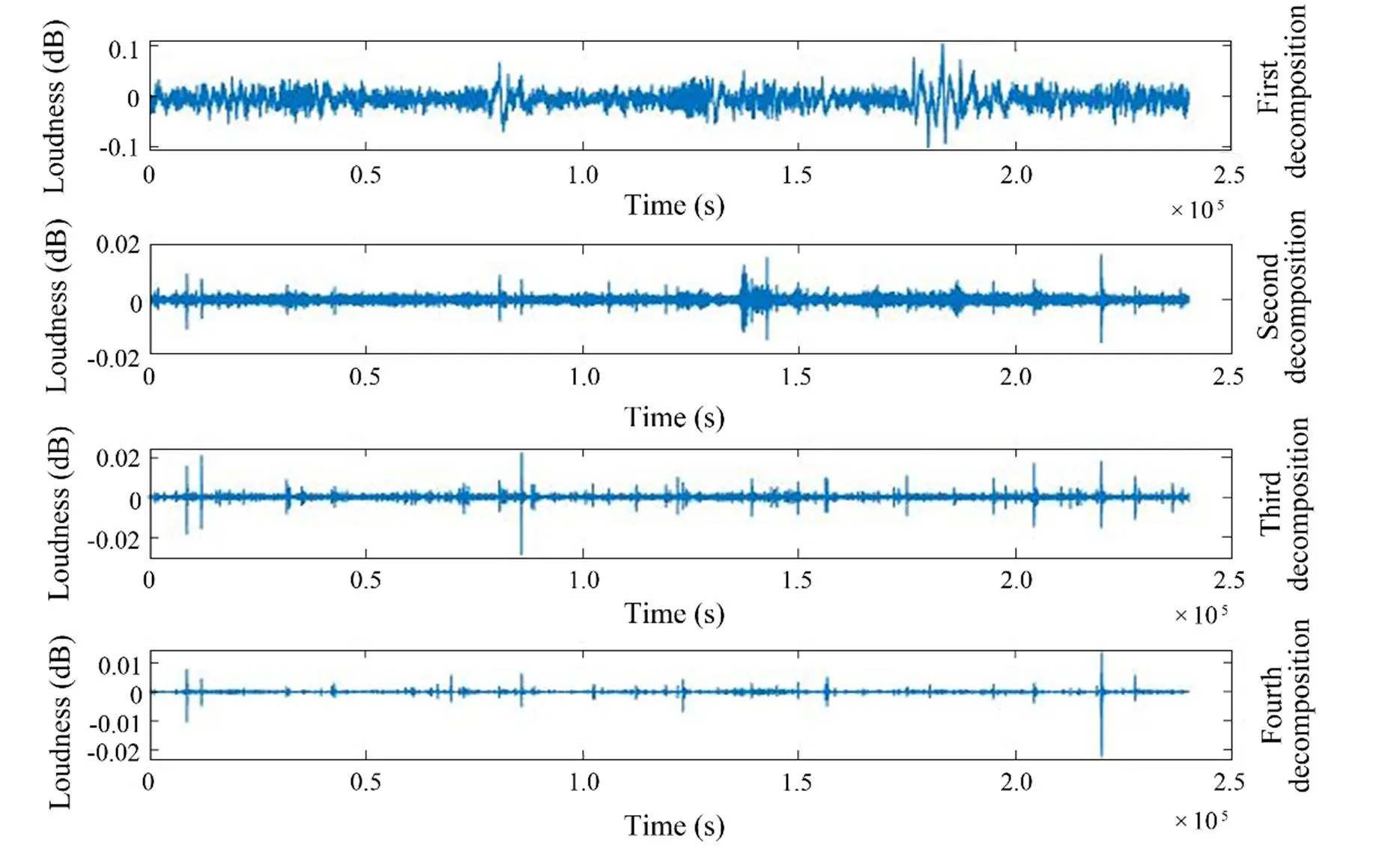
Fig.2 Waveforms of underwater acoustic signals under different states.
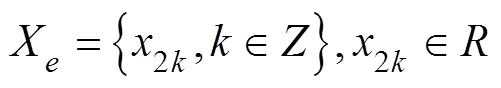
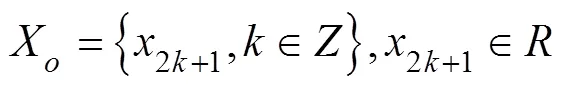
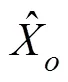
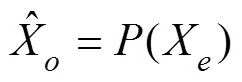

Among them,(?) is the predictor, as shown in Eqs. (6) and (7):
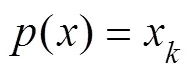
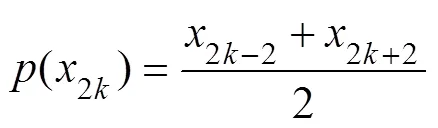
In the process of transformation, the frequency characteristic ofXis maintained, and the updater(?) is introduced. Thus, Eq. (8) holds
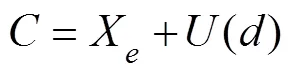
Among them, the update method can be selected from the following two functions, as shown in Eqs. (9) and (10):
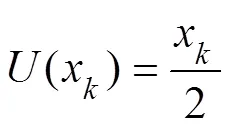
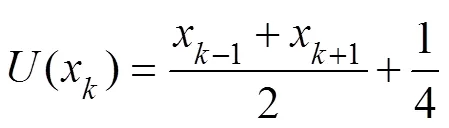
The second step is the underwater acoustic signal sequenceextraction, as shown in Fig.2. This step reflects the temporal state transformation of a segment of the signal (Hu.,2007). Different decomposition methods can be established to obtain highly detailed information regarding this signal.
The thresholdof coefficients is determined by Eqs. (11) and (12). The features of the signal sequence can be effectively extracted by setting the thresholdas follows:
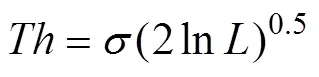
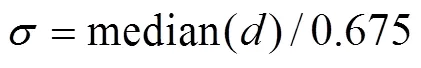
whereis the data length of the detail signal sequence={(),=1, 2, 3, ???,}and the thresholdprocessing method is shown in Eq. (13):
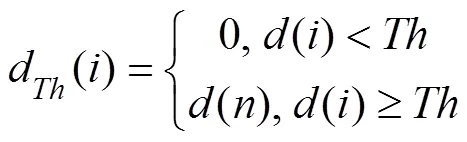
whered() is the detail signal after threshold processing and is then reconstructed by Eqs. (14) and (15) to obtain the signal:
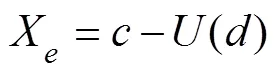
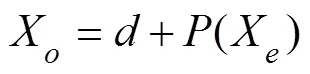
The third step is to extract the spectrogram features of the signal after the first two steps. Different wavelet bases (Bayes, BlockJs, FDR, Minimax, SURE, Universal Thres- hold) are selected to extract signal details, and low-fre- quency analysis recording is then employed to extract the spectrogram features of the signal. Fig.3 shows the waveform features of the input signal. Different waveform features can be obtained by setting different wavelet bases (Li., 2019). Afterward, the spectrogram features are obtained through low-frequency analysis recording, as shownin Fig.4, and the spectrogram features of the signal are usedas the fully convolutional encoder-decoder neural network input to train the model.
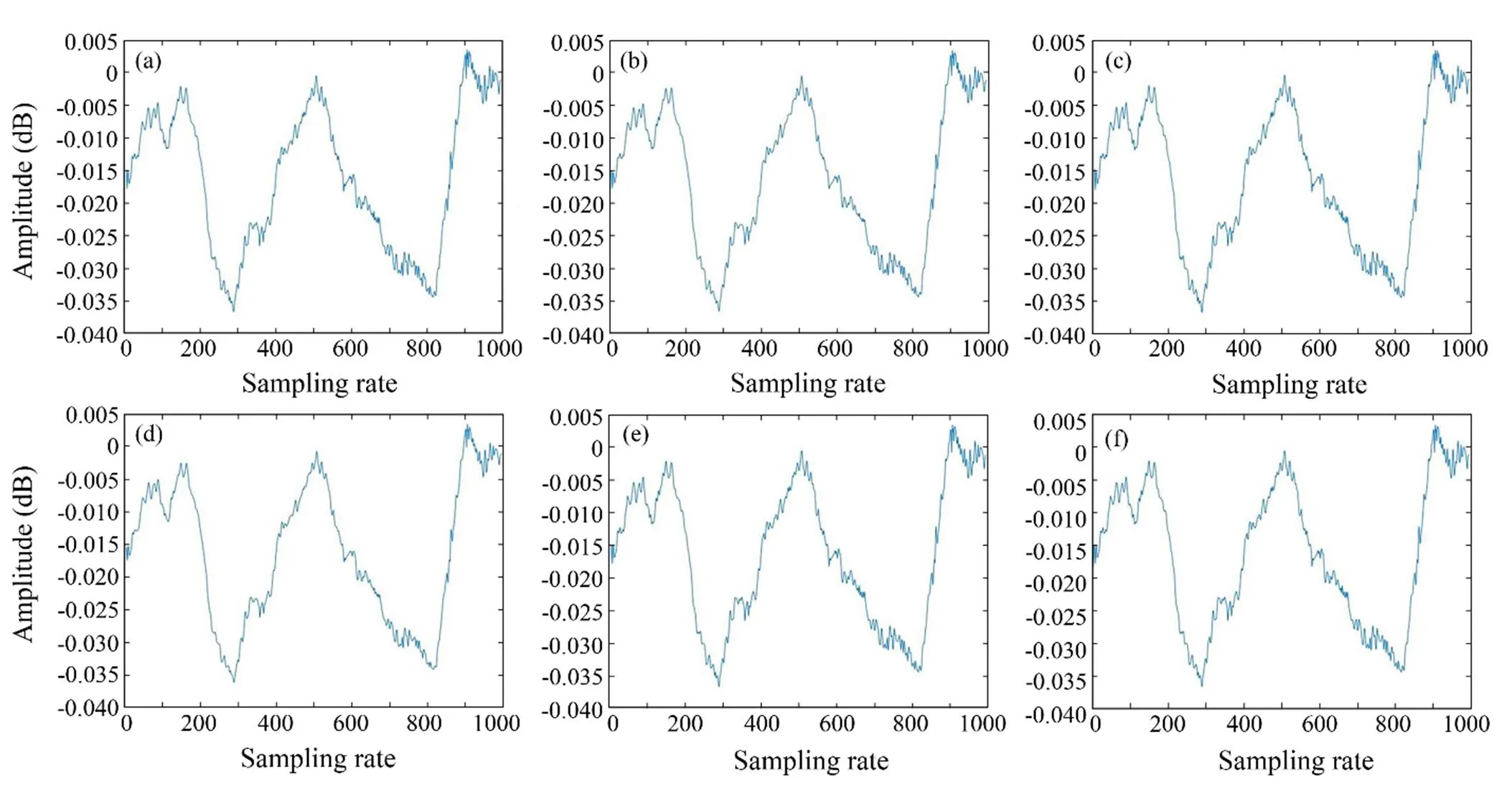
Fig.3 Waveform characteristics based on different wavelet bases. (a), Bayes; (b), BlockJS; (c), FDR; (d), Minimax; (e), SURE; (f), Universal threshold.
2.3 Fully Convolutional Encoder-Decoder Neural Network
A fully convolutional encoder-decoder neural network structure is constructed as a denoising base model. This structure improves the performance of the denoising modelby altering the network architecture or configuring various hyperparameters. Different network layers play various roles in the denoising process. The convolutional layer can be set with different kernel sizes to extract the local inva- riant features of the spectrogram. The encoder-decoder can be introduced to increase the weights of the relevant vectors and the feature aggregation of the local features extracted from the network. First, the acquired wavelet low- frequency analysis recording spectrogram features are used as input to the model. The encoding phase of the signal involves extracting its high-order features using successive one-dimensional convolutional networks that have been previously defined. Afterward, the input is fed into the fully convolutional mapping structure. The structure is then used to learn the high-dimensional mapping relationship between the noise and target signals. Finally, the acquired mapping features are converted into a time-series vector that can be used to generate audio files through a transposed convolution operation. The specific model architecture is shown in Fig.5.
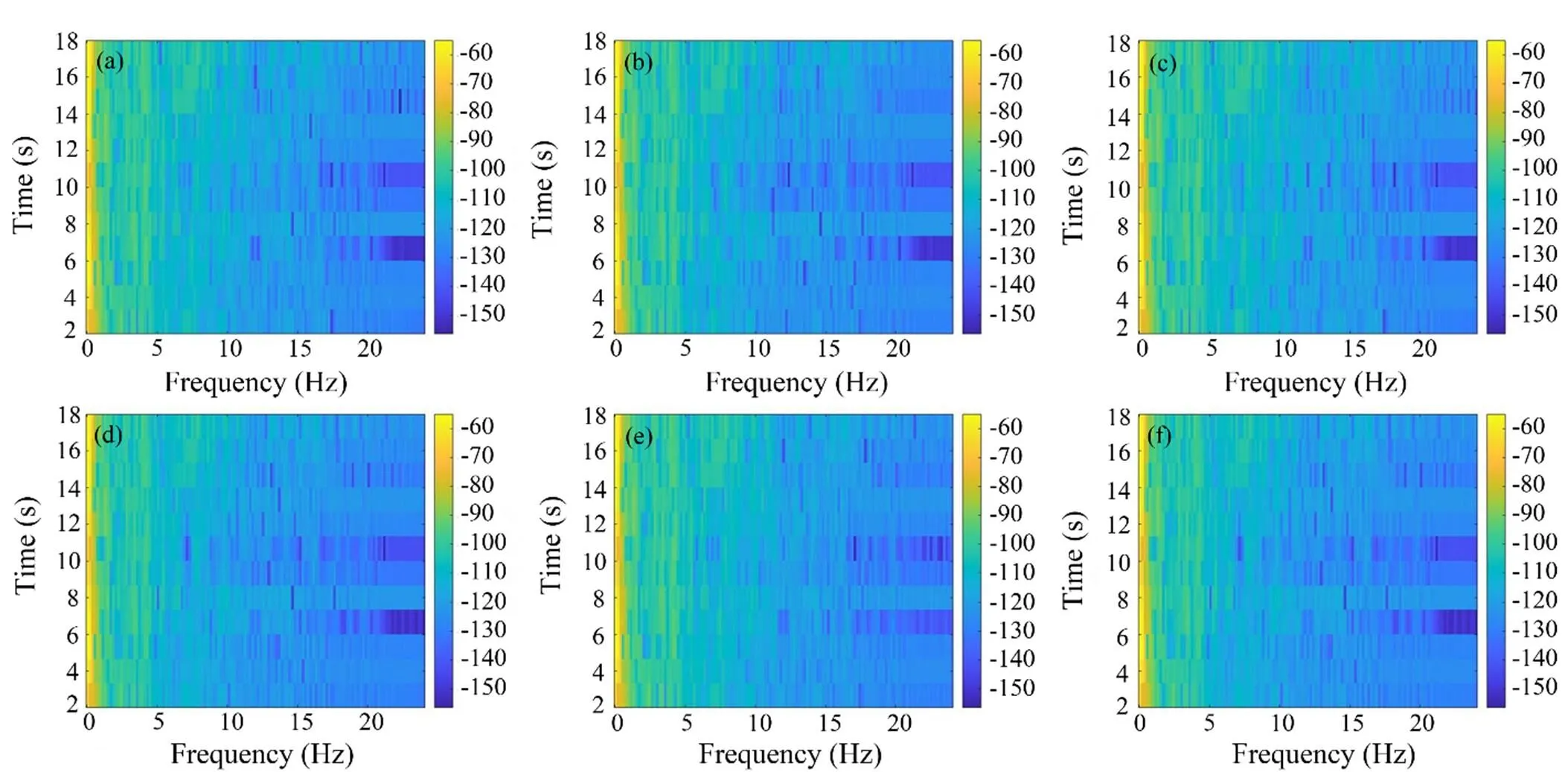
Fig.4 Spectrogram features based on different wavelet bases. (a), Bayes; (b), BlockJS; (c), FDR; (d), Minimax; (e), SURE; (f), Universal Threshold.
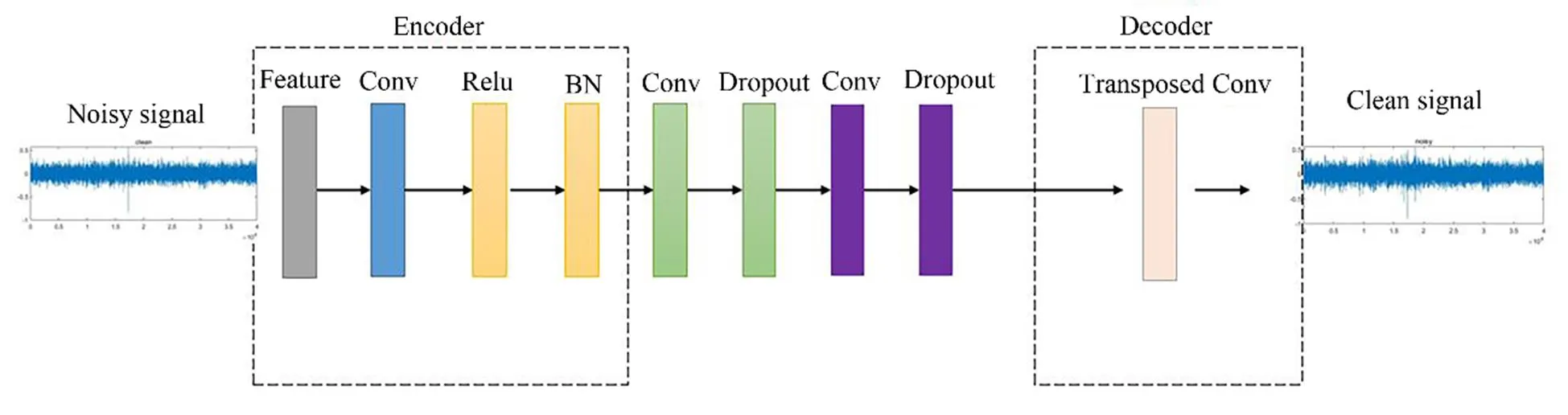
Fig.5 Fully convolutional encoder-decoder network.
The fully convolutional encoder-decoder neural networkhas three primary operations: 1) Encoder. The convolutional layers and activation functions reduce the size of the feature map. Therefore, the input spectrogram can become a low-dimensional representation and introduce a normalization method to prevent gradient disappearance. 2) Network separation module. The intermediate network layers can be adapted to any size of the input by removing the fully connected layer and replacing it with a convolutional layer. 3) Decoder. The transposed operation progressively recovers the spatial dimension. The decoder extracted the fixed length feature during the encoder-decoder process to complete the same size input and output with the least amount of information loss possible. The different parameters are described in Table 1. Where FCEDN3-8 means choosing the convolution kernel of size 3×3 and repeating the convolution operation eight times. FCEDN3-16 meanschoosing the convolution kernel of size 3×3 and repeatingthe convolution operation 16 times. FCEDN5-8 means choo- sing the convolution kernel of size 5×5 and repeating the convolution operation eight times. FCEDN5-16 means choo- sing the convolution kernel of size 5×5 and repeating the convolution operation 16 times.

Table 1 Fully convolutional encoder-decoder network (FCEDN) structure
3 Experiment
The ShipsEar dataset is presented in this section, and the experimental findings of underwater acoustic signal de- noising using it as test data are discussed (Santos., 2016). Different evaluation metrics are used to represent the effect of the noise reduction experiment (Yaman., 2021). Various outcomes from the investigations intothe reduction of underwater acoustic signal noise are shown in some ablation experiments.
3.1 Dataset
The dataset was collected with recordings made by hy- drophones deployed from docks to capture different vessel speeds and cavitation noises corresponding to docking or undocking maneuvers. The recordings are of actual vessel sounds captured in a real environment. Therefore, the an- thropogenic and natural background noise and vocalization of marine mammals are present. The dataset comprises90 recordings in .wav format with five major classes. Each major class contains one or more subclasses; the duration of each audio segment varies from 15s to 10min, and the appearance of different ships is shown in Fig.6.

Fig.6 Ships.
Each class is divided, as shown in Table 2. Class A com- prises dredgers, fishing ships, mussel ships, trawlers, and tug ships. Class B comprises motorboats, pilot ships, and sailboats. Class C comprises passenger ferries. Class D com- prises ocean liners and RORO vessels. Class E is the natural noise, and we mix it with the first four classes to construct targets containing noise, and the numbers represent the length of the signal time. A noise-laden data set containing a mixture of two acoustic signals was constructed to validate the denoising performance of the model effectively. All signals were segmented at a fixed time of 5s, re- sulting in a total of 1956 labeled sound samples. Sample without the noise class were randomly selected from the data and fused with the target samples of the noise class. Therefore, the signal-to-noise ratio of fused signals was 0dB. Afterward, the dataset was divided into validation, testing, and training sets in the ratio of 1:1:8, respectively, to verify the denoising performance of the model.

Table 2 Datasets of ShipsEar
3.2 Configuration
All networks are trained using backpropagation and gra-dient descent for batch normalization added after each convolutional layer in the mapping network. The optimization algorithm chooses an adaptive moment estimation algorithm that combines the first and second gradients(Wang, 2020). This article sets the exponential decay rates of the first- and second-order moment estimations to 0.9 and 0.999, respectively, for the setting of some specific parameters based on experience. The rates frequently lie infinitely close to 1 in sparse gradients. The sample rate is set to 44100, and the epoch is set to 50. The learning rate is reduced to 0.0001, which is then minimized by 25% from its initial value. The sampling rate is reduced by 25%, and the learning rate is reduced by 10% when the entire experiment is overfitted.
3.3 Experimental Evaluation
Training the end-to-end learning framework aims to ma- ximize the source-to-distortion ratioand the scale- invariant source-to-noise ratio. These ratios are commonly used as an evaluation metric for signal noise reduction. Therequires knowledge of the target and enhanced signals. It is an energy ratio, expressed in dB, between the energy of the target signal contained in the enhanced signal and the energy of the errors. Compared to the,uses a single coefficient to account for scaling discrepancies. The scale invariance is ensured by normalizing the signal to zero-mean before the calculation. A large scale of invariance is reasonable.andare defined as
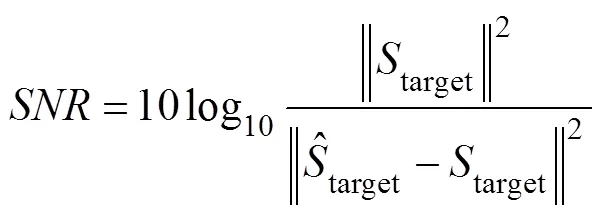
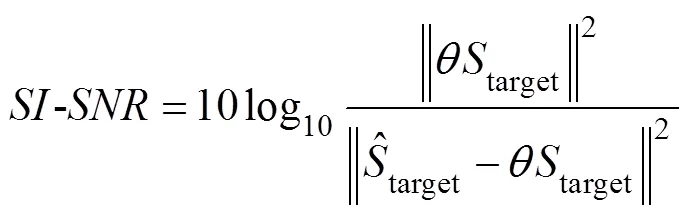
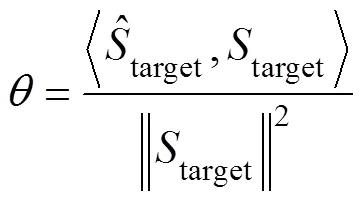
3.4 Results
Some ablation experiments were performed to compare the efficiency of denoising by introducing various models to confirm the validity of the proposed model. Tables 3 and 4 show the results achieved when applying the FCEDN- 3-8 construction to implement noise reduction for different target classes. Table 4 demonstrates the use of Class B as a test set to verify the noise reduction performance of the different base models. The base model mainly comprises interval-dependent denoising (IDD) (Yan, 2019), fully connected network (FCN) (Russo., 2021), con- volutional network (CNN), and wavelet denoising (WD) (Huang., 2012).
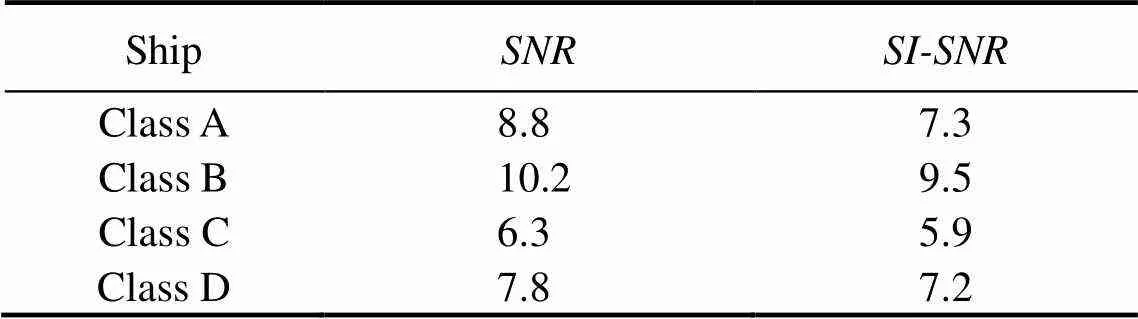
Table 3 Results of different targets
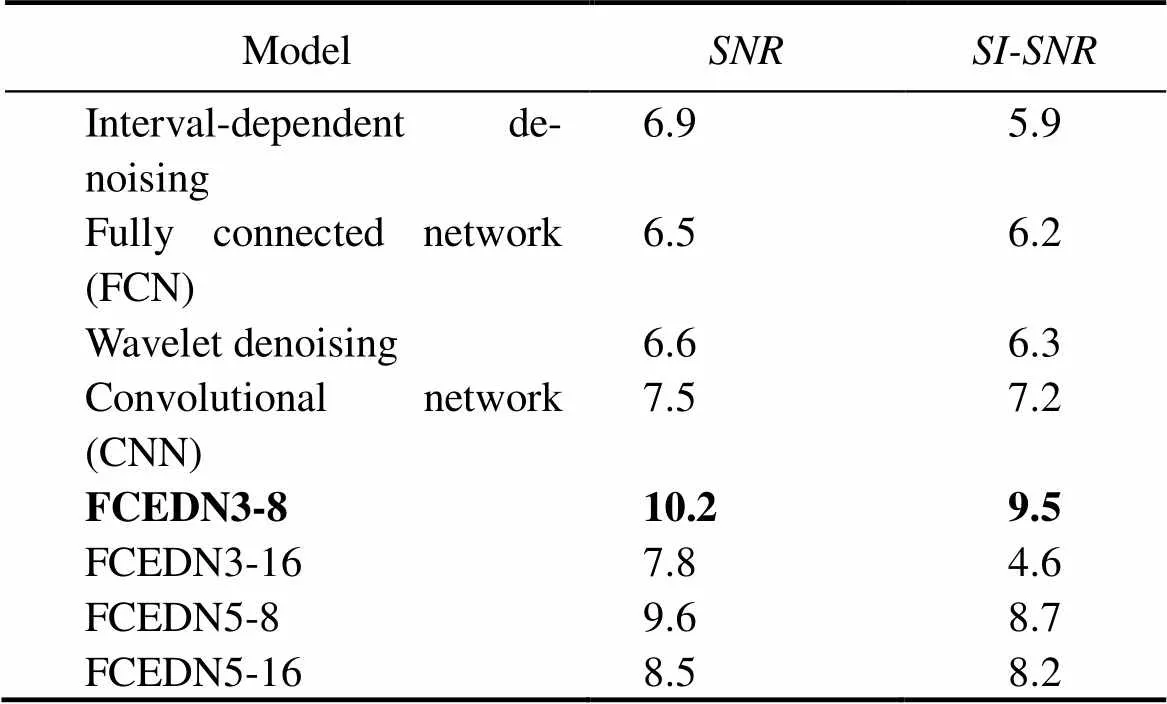
Table 4 Results of different noise reduction methods
The experimental results reveal the following:
1) A random selection of ambient natural sounds as perturbations was used to verify whether the model has a de- noising performance. Table 3 reveals that using FCEDN3-8to reduce natural environment noise can increase targetsignal SNR and SI-SNR by an average of 8.3 and 6dB, re- spectively. Therefore, using FCEDN3-8 significantly improves the target signal after processing various classes of the noisy signal.
2) The denoising of underwater acoustic signals can be significantly influenced by various network layer depths, layer structures, number of filters, filter width design me- thods, and filtering methods. Furthermore, the characteris-tic expression of energy transfer is significantly attenuatedwhen the number of layers reaches a particular range. There- fore, the impact of 3×3 and 5×5 convolution kernels and the iterations on experimental outcomes were compared, as shown in Table 4. The best results were achieved during the construction of the network with eight iterations of the 3×3 convolutional kernel. The model can extract local fea- tures precisely using small convolutional kernels, increasing the generalizability of the model. However, the model may be overfitted when the number of iterations is too high.Therefore, considering various factors, model sizes, and de- noising effects, FCEDN3-8 was selected as the model ar- chitecture method.
3) The full convolutional layer and the small kernel are used to construct the denoised network, which produces the best performance when compared to other base models. As shown in Fig.7, the FCEDN3-8 can steadily improve the signal-to-noise ratio during model training when convergence is reached after approximately 45 epochs. The FCN converges slowly during model training (Sutskever and Hinton, 2014). Therefore, the convolutional layer decreases the resource requirements of the model compared with the connected layer when the parameters are trained. Therefore, the full convolution operation of other models is replaced with successive convolution kernels, which is a practical and innovative step. Moreover, the continuous convolution kernel deepens the stack of network layers, allowing the parameters to grow linearly rather than exponentially during the forward pass.
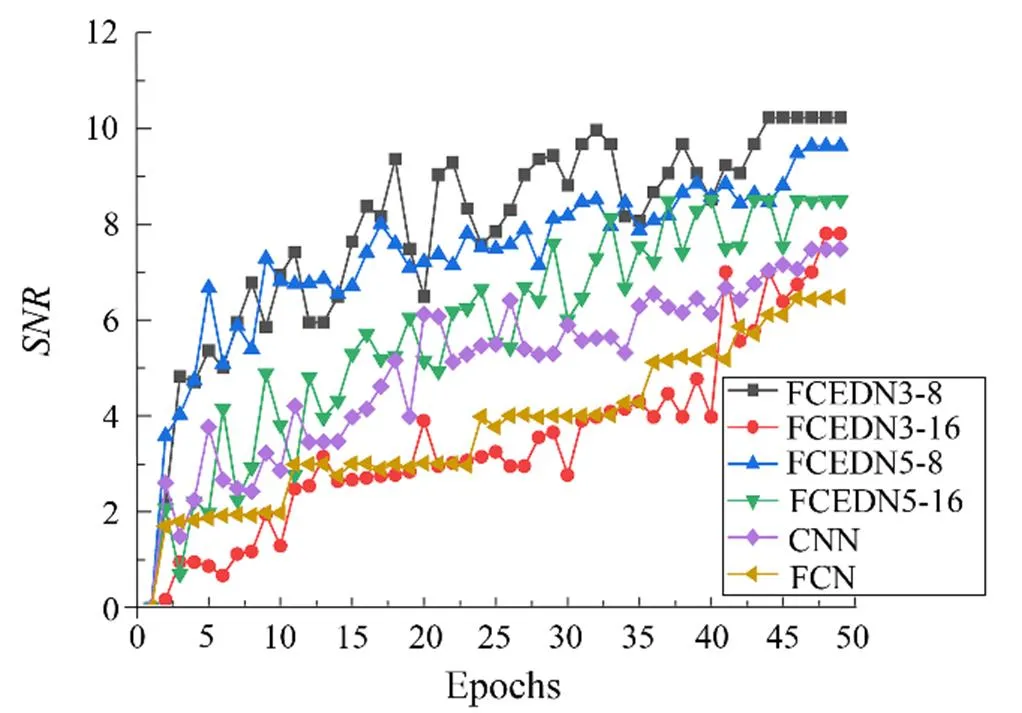
Fig.7 Noise reduction process for different methods.
4) As shown in Figs.8–11, the noise reduction effect of FCEDN3-8 can be confirmed by observing the change in the waveform and spectrogram of the signal. The original signal sampling rate was too high, and the feature information was not readily apparent. Thus, the classification network cannot accept the original signal directly. The signal features are usually extracted in spectrograms for classification experiments. The time-frequency analysis method provides joint information in the time and frequency domains, which can describe the relationship between the signal frequency and time change and thus determine the type of signal. However, spectrogram analysis cannot re- liably identify the signal class due to the inherent environmental noise (the top side of the figure shows the waveform map and spectrum of the target signal covered by noise). The low side of the figure shows the waveform and spectrogram of the signal after processing with FCEDN3-8. Different classes of underwater acoustic signals have been distinguished due to the noise reduction effect. Afterward, the acoustic generation mechanism and propagation law of ship noise were analyzed in combination with the underwater acoustic channel, and the particular time-frequency distribution difference was used for further signal detection and classification tasks.
5) The effects of different noise reduction signals on the classification results are verified, as shown in Table 5. In addition, the classification confusion matrix of FCEDN3-8 models before and after noise reduction is presented, as shown in Figs.12 and 13, respectively.
We adopt statistical sampling method where the model randomly selects different classes of denoised acoustic signals to validate the effectiveness of the noise reduction method. The validation model was chosen as the classical LSTM (Liu, 2021). The confusion matrix is used to describe the experimental results of the classification. According to Table 5, the accuracy of the LSTM model can reach 76.18% when the signal has been reduced for noise using the FCEDN3-8 method. The horizontal and vertical coordinates represent the predicted and true classes, respectively. The findings indicate that denoising improves accuracy by approximately 8%. In particular, the classification accuracy for Classes D and A increased from 67.9% to 79.4% and from 49.2% to 60.6%, as shown in Figs.12 and 13,respectively.
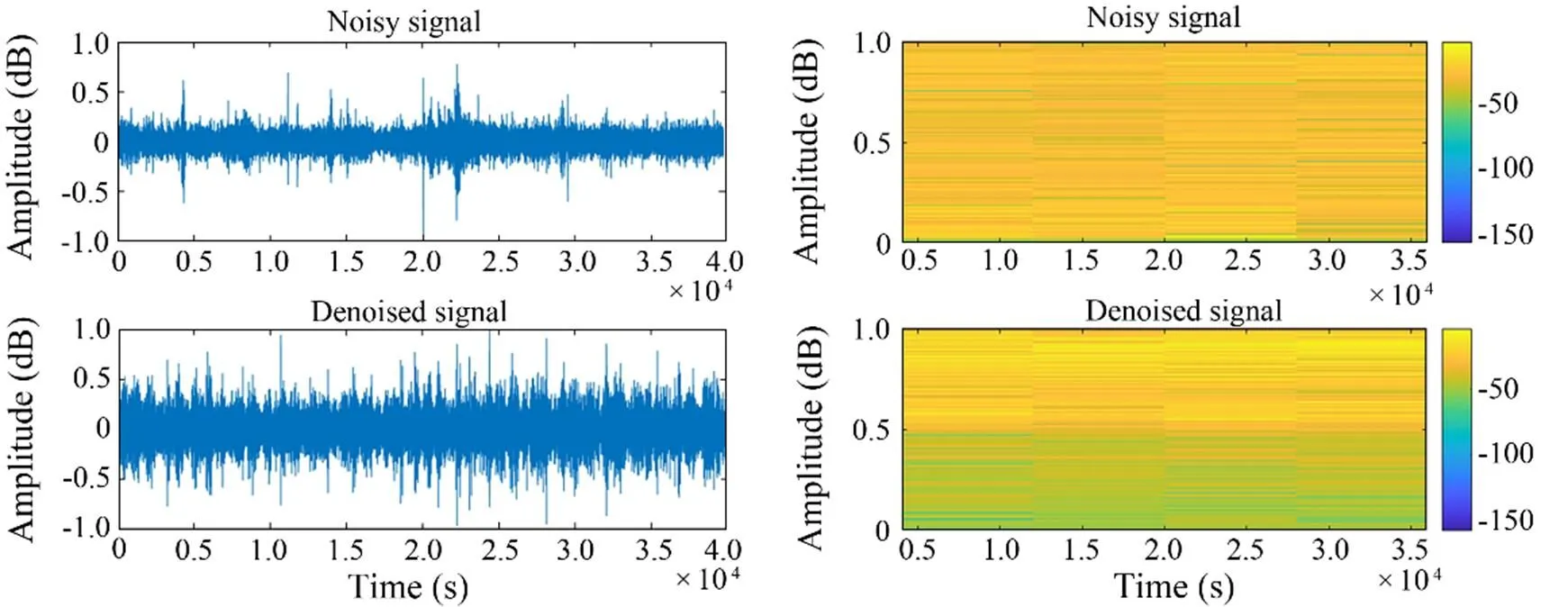
Fig.8 Class A signal waveform diagram and spectrogram.
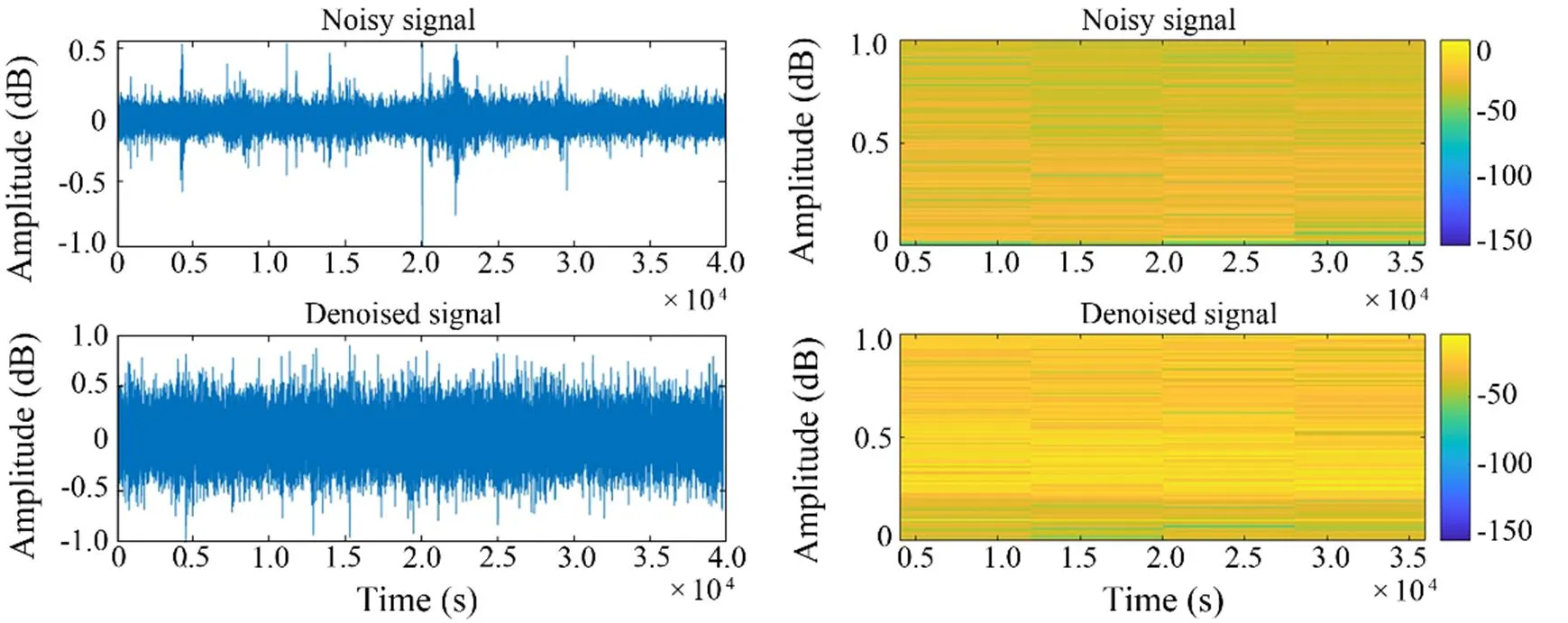
Fig.9 Class B signal waveform diagram and spectrogram.
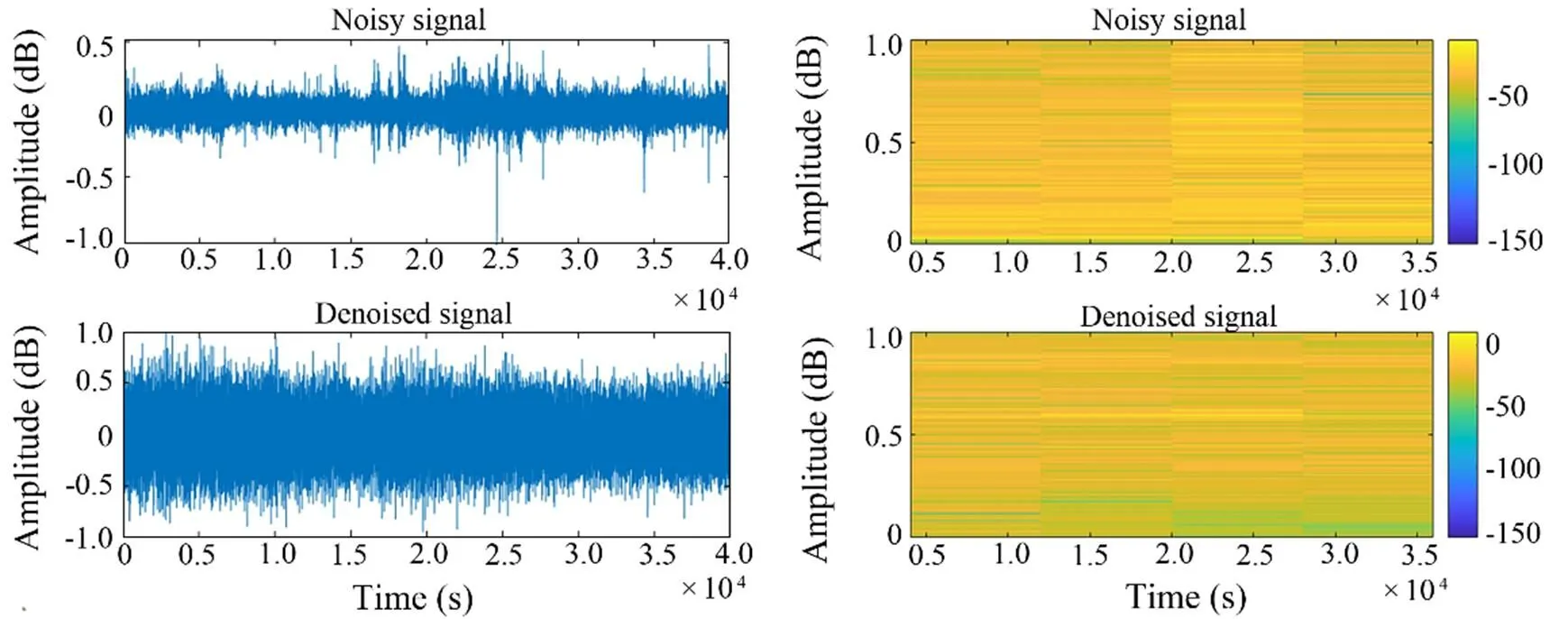
Fig.10 Class C signal waveform diagram and spectrogram.
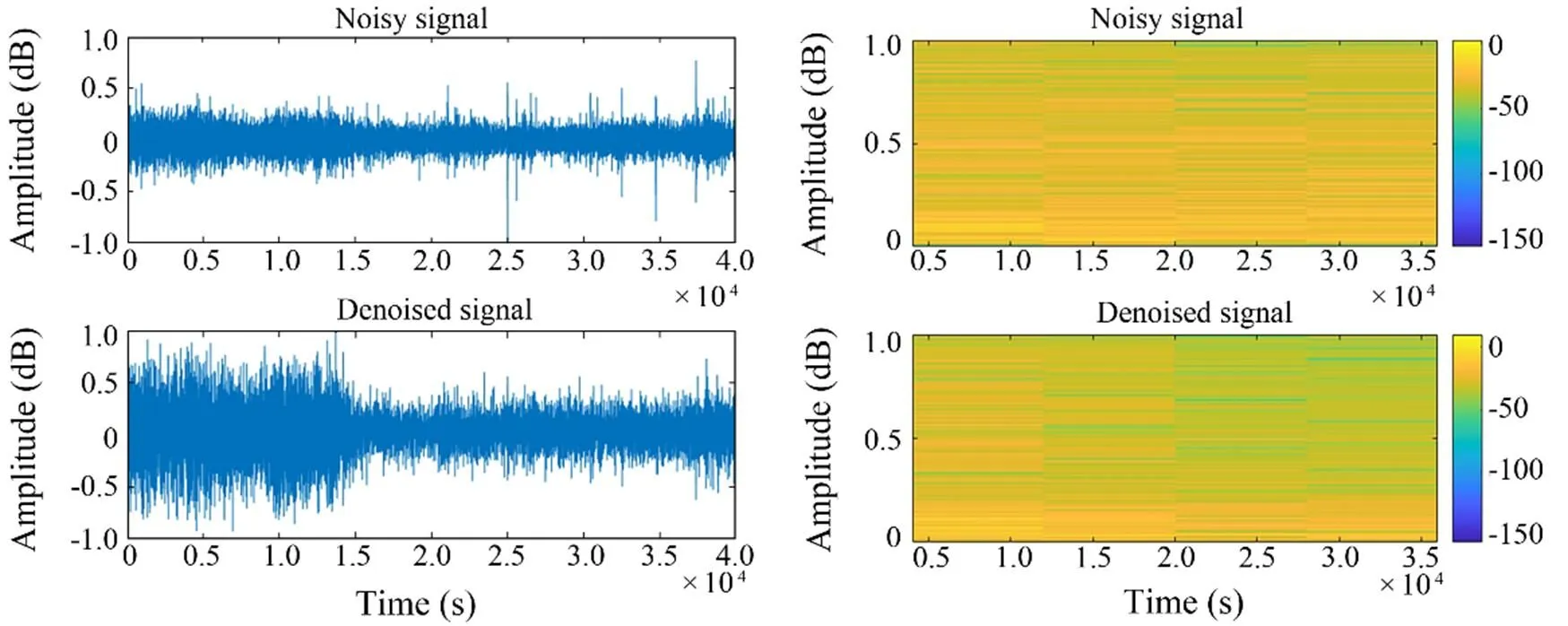
Fig.11 Class D signal waveform diagram and spectrogram.

Table 5 Classification results after noise reduction
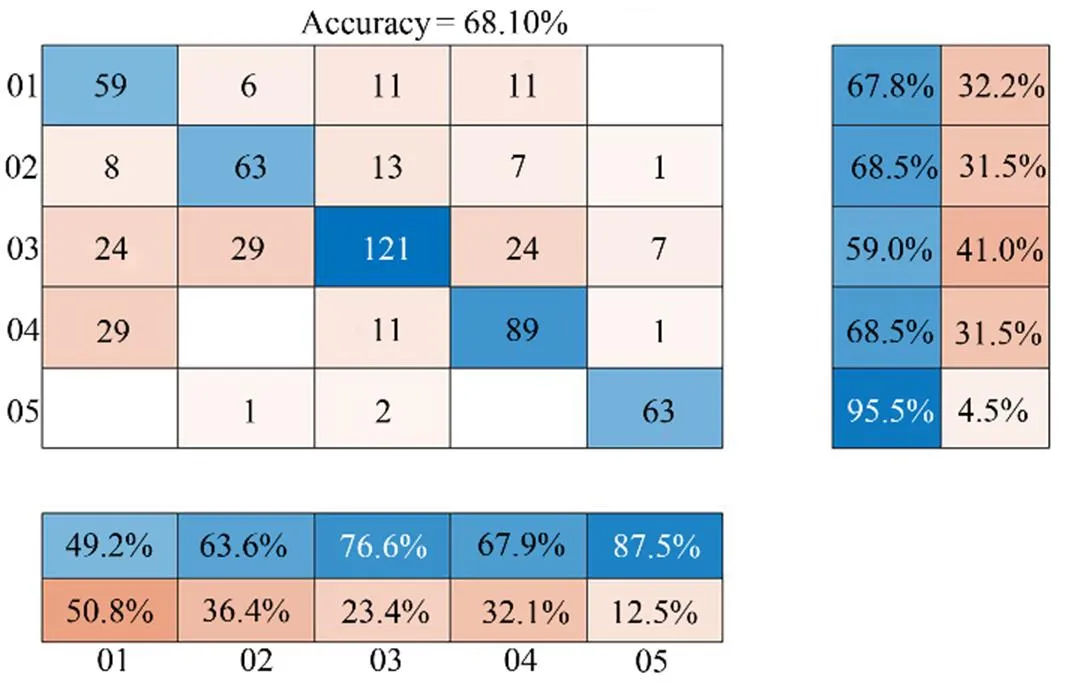
Fig.12 Classification results before underwater acoustic sig- nal noise reduction.
4 Conclusions
Noise reduction processing for underwater acoustic signals is implemented in this paper using deep learning techniques, and the FCEDN is proposed. The model is an end- to-end underwater acoustic signal denoising algorithm witha noise-containing signal at the input and a denoised signal at the output. Wavelet decomposition and low-frequency analysis theories are used to extract the features of the underwater acoustic signal. Deep neural networks are em- ployed to create the separation module between the target and noise signals. Meanwhile, the fully convolutional net- work structure is used to construct the mapping separation module based on an encoder-decoder neural network. This technique can successfully perform robust feature ex- traction and signal-to-noise separation for noisy underwater acoustic targets. The evaluation results were tested on the ShipsEar dataset, which can enhance theandto 10.2 and 9.5, respectively.
Acknowledgements
The study is supported by the National Natural Science Foundation of China (No. 41906169), and the PLA Aca- demy of Military Sciences.
Chen, H., Miao, F., Chen, Y., Xiong, Y., and Chen, T.,2021. A hyperspectral image classification method using multifeature vectors and optimized KELM., 14: 2781- 2795.
Hao, X., Zhang, G., and Ma, S., 2016. Deep learning., 10 (3): 417-439.
Hinton, G., Vinyals, O., and Dean, J., 2015. Distilling the knowledge in a neural network., 14 (7): 38-39.
Hu, Q., He, Z., Zhang, Z., and Zi,Y., 2007. Fault diagnosis of rotating machinery based on improved wavelet package transform and SVMs ensemble., 21 (2): 88-705.
Huang, H. D., Guo, F., Wang, J. B., and Ren, D. Z., 2012. High precision seismic time-frequency spectrum decomposition me- thod and its application., 47 (5): 773-780.
Klaerner, M., Wuehrl, M., Kroll, L., and Marburg, S.,2019. Ac- curacy of vibro-acoustic computations using non-equidistant frequency spacing., 145: 60-68.
Le, C., Zhang, J., Ding, H., Zhang, P., and Wang, G., 2020. Preliminary design of a submerged support structure for floating wind turbines., 19 (6): 49-66.
Li, H., Zhang, S., Qin, X., Zhang, X., and Zheng, Y., 2019. Enhanced data transmission rate of XCTD profiler based on OFDM., 18 (3): 1-7.
Liu, F., Shen, T., Luo, Z., Zhao, D., and Guo, S., 2021. Underwater target recognition using convolutional recurrent neural networks with 3-D Mel-spectrogram and data augmentation., 178: 107989.
Qiu, Y., Yuan, F., Ji, S., and Cheng, E., 2021. Stochastic resonance with reinforcement learning for underwater acoustic com- munication signal., 173: 107688.
Russo, P., Di Ciaccio, F., and Troisi, S., 2021. DANAE++: A smart approach for denoising underwater attitude estimation., 21: 1526.
Santos-Domínguez, D., Torres-Guijarro, S., Cardenal-López, A., and Pena-Gimenez, A., 2016. ShipsEar: An underwater vessel noise database., 113: 64-69.
Stulov, A., and Kartofelev, D., 2014. Vibration of strings with nonlinear supports., 76 (1): 223-229.
Sutskever, I., and Hinton, G. E., 2014. Deep, narrow sigmoid belief networks are universal approximators., 20 (11): 2629-2636.
Taroudakis, M., Smaragdakis, C., and Chapman, N. R., 2017. De- noising underwater acoustic signals for applications in acoustical oceanography., 25 (2): 1750015.
Vincent, E., Gribonval, R., and Févotte, C., 2006. Performance measurement in blind audio source separation., 14 (4): 1462-1469.
Wang, S., and Zeng, X., 2014. Robust underwater noise targets classification using auditory inspired time-frequency analysis., 78: 68-76.
Wang, X., Zhao, Y., Teng, X., and Sun,W., 2020. A stacked convolutional sparse denoising autoencoder model for underwater heterogeneous information data., 167: 107391.
Wu, D., and Wu, C.,2022. Research on the time-dependent split delivery green vehicle routing problem for fresh agricultural products with multiple time windows., 12 (6): 793.
Xing, C., Wu, Y., Xie, L., and Zhang, D., 2021. A sparse dictionary learning-based denoising method for underwater acoustic sensors., 180:108140.
Yaman, O., Tuncer, T., and Tasar, B., 2021. DES-Pat: A novel DES pattern-based propeller recognition method using under- water acoustical sounds., 175: 107859.
Yan, H., Xu, T., Wang, P., Zhang, L., Hu, H., and Bai, Y., 2019. MEMS hydrophone signal denoising and baseline drift removal algorithm based on parameter-optimized variational mode de- composition and correlation coefficient., 19 (21): 4622.
Yang, W., Chang, W., Song, Z., Zhang, Y., and Wang, X., 2021. Transfer learning for denoising the echolocation clicks of fin- less porpoise () using deepconvolutional autoencoders., 150 (2): 1243-1250.
Yao, R., Guo, C., Deng, W., and Zhao, H. M., 2022. A novel mathematical morphology spectrum entropy based on scale- adaptive techniques., 126: 691-702.
Zhao, Y. X., Li, Y., and Wu, N., 2021. Data augmentation and its application in distributed acoustic sensing data denoising., 288 (1): 119-133.
Zhou, X., and Yang, K., 2020. A denoising representation fra- mework for underwater acoustic signal recognition., 147 (4): 377-383.
Zhou, X., Ma, H., Gu, J., Chen, H., and Wu, D., 2022. Parameter adaptation-based ant colony optimization with dynamic hybrid mechanism., 114:105139.
(June 30, 2022;
August 25, 2022;
February 15, 2023)
? Ocean University of China, Science Press and Springer-Verlag GmbH Germany 2023
. E-mail: 1609217323@qq.com
(Edited by Chen Wenwen)
 Journal of Ocean University of China2023年6期
Journal of Ocean University of China2023年6期
- Journal of Ocean University of China的其它文章
- Effects of 5-Azacytidine (AZA) on the Growth, Antioxidant Activities and Germination of Pellicle Cystsof Scrippsiella acuminata (Diophyceae)
- Improving Yolo5 for Real-Time Detection of Small Targets in Side Scan Sonar Images
- Wave Radiation by a Floating Body in Water of Finite Depth Using an Exact DtN Boundary Condition
- Revisiting the Seasonal Evolution of the Indian Ocean Dipole from the Perspective of Process-Based Decomposition
- Assessment of Storm Surge and Flood Inundation in Chittagong City of Bangladesh Based on ADCIRC and GIS
- Contraction of Heat Shock Protein 70 Genes Uncovers Heat Adaptability of Ostrea denselamellosa
