Team-based fixed-time containment control for multi-agent systems with disturbances
Xiao-Wen Zhao(趙小文), Jin-Yue Wang(王進月), Qiang Lai(賴強), and Yuan Liu(劉源)
1School of Mathematics,Hefei University of Technology,Hefei 230601,China
2School of Electrical and Automation Engineering,East China Jiaotong University,Nanchang 330013,China
Keywords: fixed-time containment control, dynamic event-triggered strategy, team-based triggered strategy,multi-agent systems
1.Introduction
The distributed cooperative control problem has attracted much attention due to its widely potential applications including smart grids,[1]deception attacks,[2]and so on.The issue of consensus control is an important part of cooperative control, and to enable the agent to follow the specified trajectory and to reach the predetermined goal,a leader-follower approach was introduced in Ref.[3], where the follower enters and follows the route designed by the leader through the information passed by the leader and eventually converges to the predetermined goal.The consensus control problem for multi-agent systems (MASs) with two or more leaders, also known as the containment control problem, has the property of guiding followers into the convex hull region formed by the leaders,which makes containment control of great interest and widely used in many real-life situations.For example,in order to avoid densely populated residential areas while removing hazardous chemicals, rescue robots must follow a designated route.The robots without sensors are steered into the convex hull that is spanned by the robots with sensors and they then advance in the convex hull region because only a few robots have sensors to monitor the surroundings.Therefore, it is of great interest to study the problem of containment control.
So far, many major and interesting findings on containment control of MASs have been found like Refs.[4-6].Notably, most of the literature focuses on the asymptotic or exponential containment control problem,which implies that the agent cannot follow the desired trajectory and achieve the desired goal in finite time.This has led some researchers to further focus on studying the finite-time containment problem for MASs.Attitude containment control of a first-order MASs with stationary leaders was studied by proposing a model-independent strategy in Ref.[7].In Ref.[8], the finite-time containment control problem for double-integral MASs with multiple dynamic leaders was discussed,and further finite-time containment control without velocity measurements was achieved in Ref.[9].However, these derived upper bounds on the convergence time were predicated on the need to know information about the initial state of the agents,which is sometimes not easy to know.Based on this, the fixed-time consensus control algorithm was further proposed in Refs.[10,11], applying this principle to MASs with one leader and multiple leaders, and successfully implemented fixed-time tracking control and fixed-time containment control(FCC)in Refs.[12-14].Considering the presence of unavoidable external disturbances in real systems, FCC with disturbances was further investigated in Refs.[15,16].
Note that all the above tasks are carried out with continuous communication.However,on the one hand,the failure of external devices may prevent communication and hinder task completion.On the other hand,continuous message monitoring inevitably consumes excessive resources.Therefore, it is important to study the containment control problem for MASs with intermittent communication.In Refs.[17,18], an eventtriggered control(ETC)mechanism for consensus control was proposed by constructing combinations of measurement errors, which implies inter-agent communication only when a specific event is triggered.Dynamic event-triggered control(DETC) is a mechanism further develop by Girardet al.in Ref.[19].It creates a new trigger function by including a dynamic variable,which has the advantage of lowering the number of controller updates.Correspondingly,ETC-based fixedtime containment control has been achieved in Refs.[20-22].However,we notice that the problem of DETC-based containment control is rarely considered.In addition,inter-state combinations using measurement errors inevitably employ adjacent relative information,which increases the problem of continuous communication to some extent.For this reason,some scholars have tried to use self-triggering methods to determine the next trigger moment directly from the current moment in Refs.[23-25], while this has the disadvantage of increasing the number of triggers.Based on this,some scholars have tried to weigh the relationship among convergence speed,communication cost and the number of triggers, and have proposed the idea of team triggering to solve this difficulty discussed in Ref.[26], which has achieved initial success in consensus control but has received little attention in containment control.
The above discussion inspires the research in this paper,which further considers the use of dynamic event-triggered strategies and team-triggered techniques to achieve FCC for MASs with disturbances.First, FCC is achieved.Unlike the fixed-time controller created in Ref.[24], on the one hand,we have no requirement for the parity of the parameters, and on the other hand, the symbolic function is replaced by the saturation function, which avoids the chattering effect that may be caused by the discontinuity of the symbolic function and also better excludes the Zeno behavior, which is also effectively illustrated in the simulation section.Second, a dynamic event-triggered algorithm is proposed to achieve FCC,which can effectively reduce controller updates.Finally, by combining the self-triggering technique with the proposed dynamic event triggering mechanism,an algorithm called teamtriggered mechanism is further designed,which does not have triggers as many as the self-triggering technique and has a faster convergence time than the proposed dynamic event triggering technique,enabling the system to make a trade-off between communication cost,convergence time and the number of triggers.Moreover,unlike the undirected graphs presented in Refs.[27-29],we discuss containment control based on directed graphs.
This paper is structured as follows.Section 2 introduces the preparatory knowledge including two parts of graph theory and problem description,the main results of this paper are presented in detail in Section 3 and the corresponding simulation results are given in Section 4, finally Section 5 is the conclusion.
2.Preliminaries and problem statement
2.1.Graph theory
Consider a directed graphG={V,A,E}withmagents,whereV,E,Adenote the set of nodesV={1,...,m},the set of edgesEV×V,and adjacency matrix A=(aij)m×mwithaij>0,if agentican obtain the information from agentj;andaij=0, otherwise.Letdi=∑mj=1,j/=i aij, the degree matrixD=diag{d1,...,dm}and the Laplacian matrixL=D-A=(lij).Furthermore,a directed graph is said to satisfy the detail balance condition if there exists some scalarμi>0 such thatμiaij=μjaji.The containment control problem studied in this paper is based on this graph-theoretic knowledge.
2.2.Problems formulation
Consider the MASs with disturbances consisting ofm(m=m1+m2) agents.Let F1={1,2,...,m1}and F2={m1+1,m1+2,...,m1+m2}represent the set of followers and leaders,respectively.Their dynamics can be expressed by
wherexi(t),ui(t)anddi(t)denote the agent state,control input and external disturbance,respectively.
Assumption 1[30]Assumed that the communication graphGF1(communication topology consisting of agents in F1)is a connected directed graph and satisfies the detail balance criterion.In addition, every leader has at least one follower as a neighbor.
Assumption 2 The external disturbance of each agentiis bounded by a non-negative constant ˉd,i.e.,for anyi ∈F1∪F2,there exists ˉd≥0 such that|di(t)|≤ˉd.
Remark 1 Herein,we further consider MASs with disturbances,which are unavoidable in practical engineering.Note that Assumption 2 has been widely used to deal with perturbation effects, and many types of nonlinear perturbations (e.g.,sinusoidal perturbations) encountered in real engineering are consistent with this assumption.What’s more, Assumption 1 is the basic condition for containment control, which ensures that each follower has direct or indirect access to leader information.
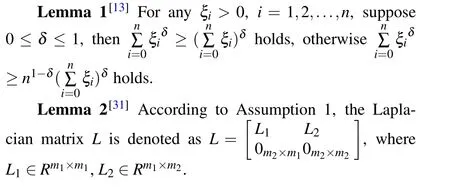

Lemma 5[33]Assuming that matrixμ= diag{μ1,...,μm1},we can obtainL1μ>0.
In what follows, the introduction of the convex hull is important for the study of containment control, Co(y) is said to be the convex hull of the sety={y1,...,yn}if it satisfies Co(y)={∑ni=1νiyi|yi ∈Y,νi ≥0,∑ni=1νi=1}.LetxF(t)=(x1(t),...,xm1(t))T,xL(t) = (xm1+1(t),...,xm1+m2(t))T, according to Lemma 2, we havexp(t)=(xp1(t),...,xpm1(t))Tinside the convex hull spanned by the leader’s state, wherexp(t)=?xL(t)∈Rm1×1.Define the containment control error as follows:?x=xF(t)-xp(t)∈Rm1×1, i.e.,?xi(t) =xi(t)-xpi(t),i ∈F1.Our goal is to design appropriate eventtriggered control protocol such that all follower agents enter and remain within the convex hull generated by the leader within a fixed time.
Definition 1 The fixed-time containment control of MASs can be achieved if there exists a constantTfor any initial states satisfying limt→T|?xi(t)|=0 and|?xi(t)|=0 for anyt ≥T,i ∈F1.
3.Main results
In this section, we propose two algorithms to achieve FCC.The first algorithm reduces the number of controller updated by designing a dynamic variable, inspired by the application of dynamic event triggering techniques in consensus control.Then,the team-triggered algorithm is further designed to implement containment control, which is a combination of a self-triggering strategy and the proposed dynamic triggering mechanism.
The fixed-time containment control protocol for each followerivia an event-triggered strategy is designed as follows:

where sign(·) denotes symbolic function.Auxiliary variableζi(t)is

withs> 0.In addition,|εi(t)|-σ?i(t) is noted as being a function triggered by a static event, marked asψi(t) ?|εi(t)|-σ?i(t).Thus,the next trigger moment is
Remark 2 Unlike the fixed-time controller created in Ref.[24], on the one hand, we have no requirement for the parity of the parameters, and on the other hand, the symbolic function is replaced by the saturation function, which avoids the chattering effect that may be caused by the discontinuity of the symbolic function, which is also effectively illustrated in the simulation section.
Lemma 6 Construct the Lyapunov candidate function as
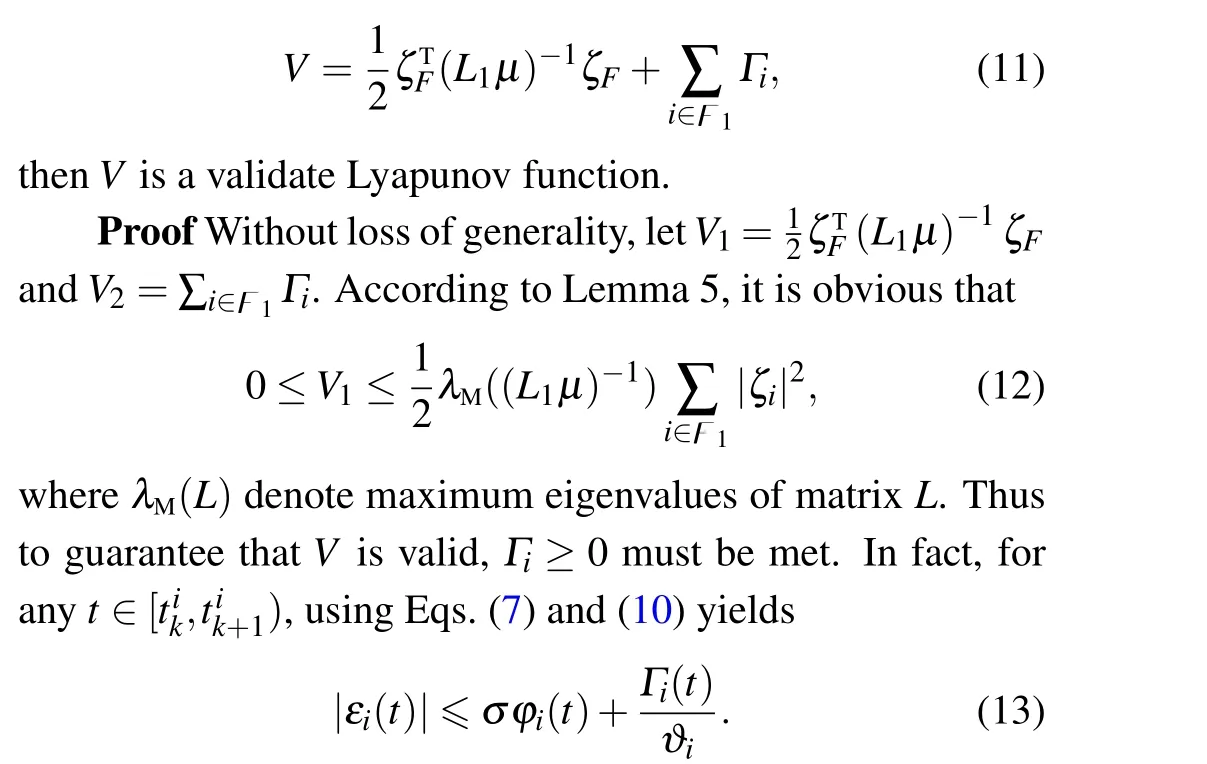
It can be further deduced that

Remark 3 Lemma 6 has shown that the constructed Lyapunov function is reasonable, and in combination with Eq.(15)we find that the dynamic variables satisfying Eq.(9)are always non-negative between any two communications of the agents,which further suggests that the average inter-event time of the dynamic event trigger Eq.(10)can be significantly increased compared to the traditional ETC mechanism.



will hold only whenζi(t)≥0, which is practically difficult to achieve, so specifying the parameterαas odd is the only way to achieve FCC in this scheme.This further shows that one of the advantages of the controller proposed in this paper is the relaxation of the requirement forα.Furthermore, it is clear that the first term of the control protocol is necessary to achieve FCC,whileκ2is used to weigh the dynamic variables.
In what follows,assume that|ζi(t)|≤δ,saturation function sat(ζi(t))=ζi(t)/δ.To distinguish the sign from that in Theorem 1,mark ?εi(t)as the new combined error,with
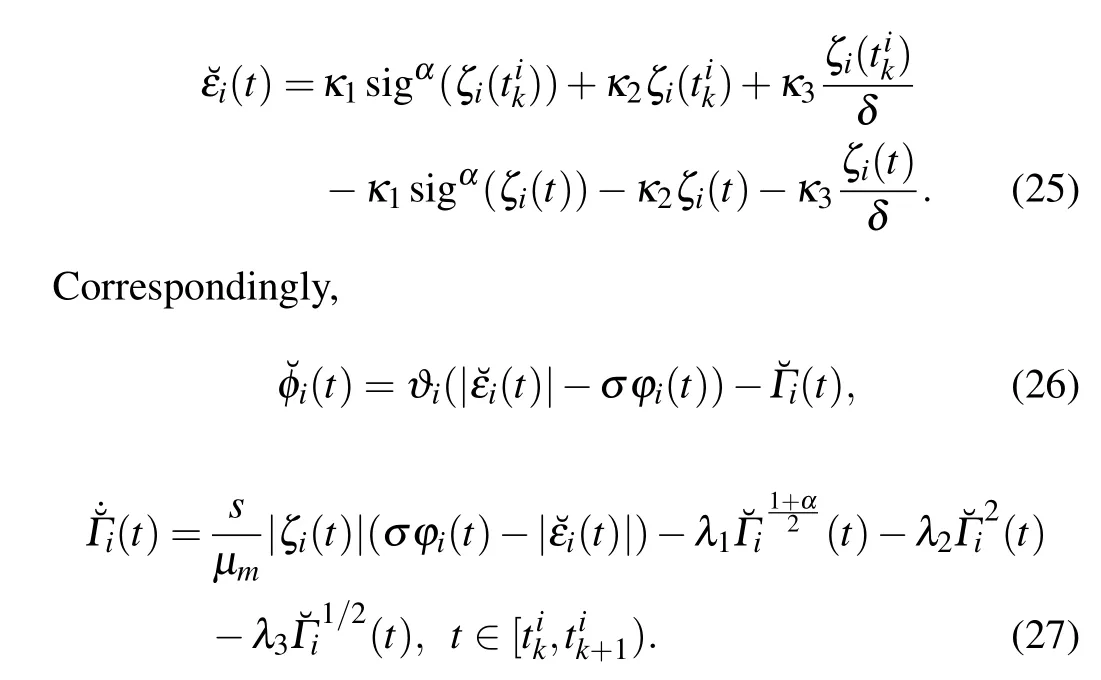
Similar to Theorem 1,the main conclusion of this scenario is given in Theorem 2.
Theorem 2 Under Assumptions 1 and 2, when|ζi(t)|≤δ, the fixed-time containment control of MASs consisting of Eqs.(1)and(2)can also be achieved under controller(3)and triggered condition(10)with the settling timeT2=2T1.
Proof Select the same Lyapunov candidate functionV,and deriving it by

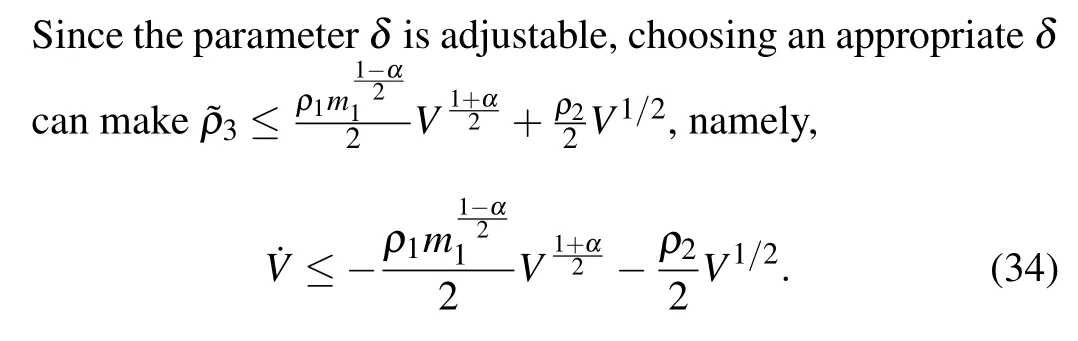
Therefore,it can be deduced from Lemma 3 that at a fixed timeV →0,it shows?xi →0 withinT2=2T1.This concludes the proof of Theorem 2.
Theorem 3 Under Assumptions 1 and 2, the fixed-time containment control of MASs consisting of Eqs.(1) and (2)can be achieved under controller (3) and triggered condition(10),and the settling timeT=3T1.
Proof From Theorem 1,it is clear that each agent will enter the|ζi(t)|≤δzone withinT1,and Theorem 2 proves that the agent can achieve fixed-time containment control within 2T1when|ζi(t)|≤δ.Therefore, combining Theorems 1 and 2 yields this theorem immediately.
Corollary 1 If the next trigger moment of each agent satisfies
the systems (1) and (2) can also achieve fixed-time containment control under controller (3) if Assumptions 1 and 2 are satisfied.
Proof Choosing the Lyapunov candidate function asV1.On the one hand,when we consider the case of|ζi(t)|≤δ,a calculation similar to Eq.(17)yields

In virtue to Lemma 3,the fixed-time containment control can be achieved.On the other hand,when|ζi(t)|>δis satisfied,the same conclusion can be obtained in a similar way to Theorem 2,and the proof is omitted here.The proof of this inference is completed.
Remark 5 In general, Eq.(35) is referred to as a static trigger condition, characterized by the fact that no dynamic variables are involved, which is obviously a special case of condition(10)whenΓi(t)=0.It can also be seen that one of the advantages of a dynamic variable-based triggering mechanism is that the triggering parameters can be dynamically adjusted to achieve the desired system performance.
Theorem 4 Under Assumptions 1 and 2,multi-agent systems (1) and (2) based on controller (3) and dynamic event triggering function(7)do not show Zeno behavior.

which means that no Zeno phenomenon will occur.
Remark 6 Note that the parameterκ3plays an important role in this paper.On the one hand,it is clear from the proofs of Theorems 1 and 2 thatκ3is not only effective in suppressing external perturbations but also key to achieving FCC.On the other hand,combined with Eq.(19),κ3ensures a positive lower bound on the event interval for each follower, thus effectively excluding Zeno behavior.
Remark 7 When executing a dynamic time trigger, it is obvious that ifφi(t)>0, there must beψi(t)>0.However,when executing a static trigger,ψi(t)>0 butφi(t)>0 unnecessarily holds, which means that Eq.(10) is a sufficient non-essential condition for Eq.(35).This illustrates that using a dynamic trigger strategy reduces the frequency of controller updates.
Remark 8 Both the event-triggering strategies (7) and(35) share the drawback that the event-triggered functionsφi(t) andψi(t) involve continuous-time adjacency information,which suggests that implementing the triggering mechanism requires continuous communication,which is preferably reduced in practical applications.
Based on the above discussion, we further designed the team trigger mechanism to trade-off convergence speed,communication cost and trigger time.Before introducing the team triggers,define a new functionπi(t),which satisfies
whereξi(t) =κ3sat(ζi(t)).Imitating the differentiation of Eq.(36)yields
The team-based trigger function is designed as


Algorithm 1 Team-based event-triggered communication and control law.Require:i At t0=0, initialize ui(0)=-κ1 sigα(ζi(0))-κ2ζi(0)-κ3 sat(ζi(0)), i ? F1.Ensure:1:2:3:4:5:6:7:8:9:10:11:12:13:14:15:16:17:18:19:i i i i For any t ? [tk, tk+1), compute |ξi(tk)| and Ξi(tk) with (43) ;if - |ξi(tk)|+η ≥ Ξi(tk) then σμm i i σμm+μM compute Γi(t) as the solution to (9)if i DET function φi(t) exceeds zeros at triggering moments t=tk then i measurement error of agent i resets to zeros at t=tk;perform xi(tk) ? xj(tk);compute auxiliary variable ζi(tk) with (4)compute control ui(t) with (3)i i i end if end if if - |ξi(tk)|+η < Ξi(tk) then σμm i i σμm+μM j compute Υ(tk′(t)) with (41);if ∫ Υ(tk′(t))ds+- |ξi(tk)|-Ξi(tk) ≥ 0 at t=tk then t j σμm i i i i tk σμm+μM i εi(t) resets to zeros at t=tk;i i perform xi(tk) ? xj(tk);i compute auxiliary variable ζi(tk) with (4)compute control ui(t) with (3)end if end if
Theorem 5 Under Assumptions 1 and 2,if the next trigger moment of each agent satisfies
the fixed-time containment control of MASs consisting of Eqs.(1)and(2)can be achieved under controller(3).In addition,Zeno behavior can be avoided.



Remark 11 If only the symbolic function sign(·)is used in Eq.(3), on the one hand, there will be unnecessary chattering due to the discontinuity in the control input that may result from the application of discontinuity function, which can be avoided by applying the saturation function,and on the other hand, the use of sat(·) will eliminate the need to calculate the derivative of sign(·),which will further help us to rule out Zeno behavior.
4.Simulation results
Consider the first-order multi-agent systems consisting of five agents with disturbance.As shown in Fig.1, assuming that 1-3 are follower agents and 4-5 represent leader agents,we can immediately obtain

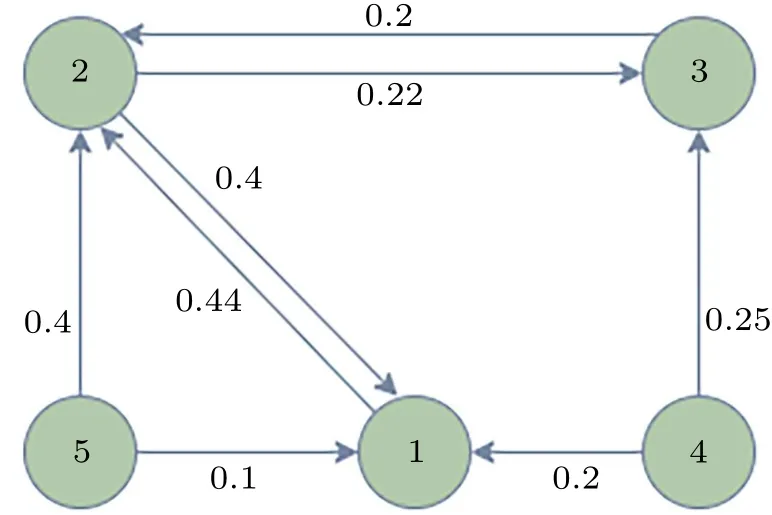
Fig.1.Communication graph.
Example 1 Containment control under DETC mechanism.
Assume thatx(0)=[9;-1.5;-12;1.5;-1.5]andΓ(0)=[10;2;3].Under the DETC condition (10), Fig.2 shows the state trajectories of all agents, and Fig.3 shows the plot of the containment error formed between the leader and the follower,which indicates that containment control is achieved at 1.190 s.This convergence time is much less than the calculated upper time limit ofT.

Fig.2.The process of state change under the DETC mechanism.
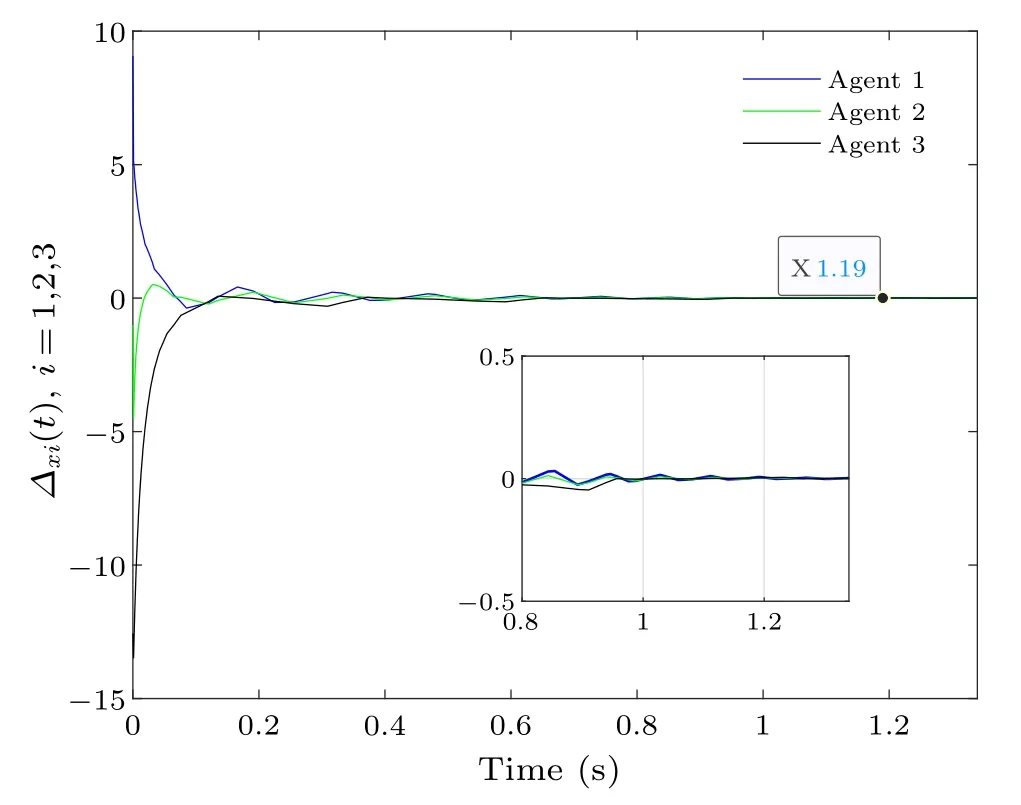
Fig.3.DETC-based containment error.
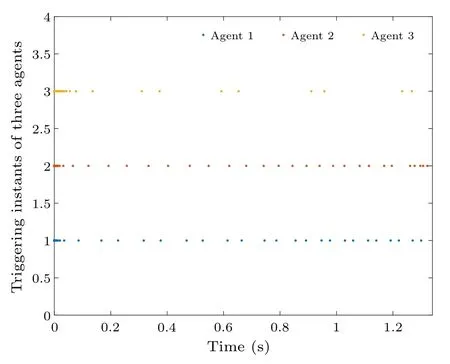
Fig.4.Trigger moments for DETC-based agents.
All trigger moments of the follower agent from 0 to 1.34 s are shown in Fig.4.It is easy to see that the triggering of the agents is not synchronized and the Zeno phenomenon does not occur.If only symbolic functions are used in Eq.(3),then the trigger moment for each agent is shown in Fig.5,which may result in triggers being triggered constantly.
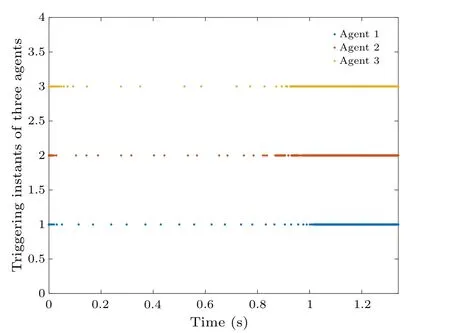
Fig.5.The trigger moment of the DETC-based agent using only the symbolic function sign(·).
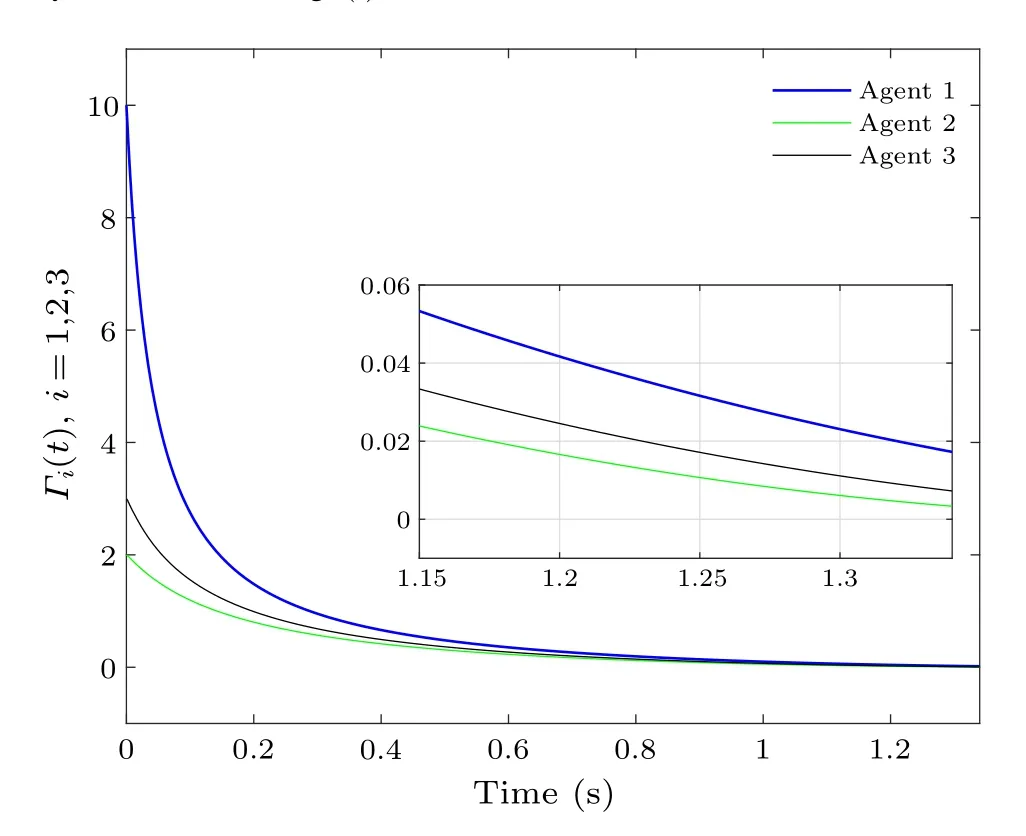
Fig.6.Evolutionary process of dynamic variables.
Figure 6 gives a graph of the evolution ofΓi(t) satisfying Eq.(9), showing that allΓi(t) are not less than 0, which further confirms the validity of Lemma 6.Take agent 3 as an example and observe the change in control input throughout the process, as shown in Fig.7, it is clear that this is a continuous function.Moreover,taking agent 2 as an example,the evolution ofΓi(t)and?(|ε2(t)|-σφ2(t))is shown in Fig.8,and it can be inferred that Zeno behavior never occurs when the containment error tends to zero.
Example 2 Containment control under team-triggered mechanism.
Choosing the same initial conditions as in Example 1,and similar to Fig.2,Fig.9 gives the state evolution process for all agents based on the team trigger conditions (44).The evolution of the containment error generated by the leader and the follower is given in Fig.10, and it is easy to see that achieving the containment control goal in about 0.844 s has a faster convergence rate compared to using the DETC mechanism.
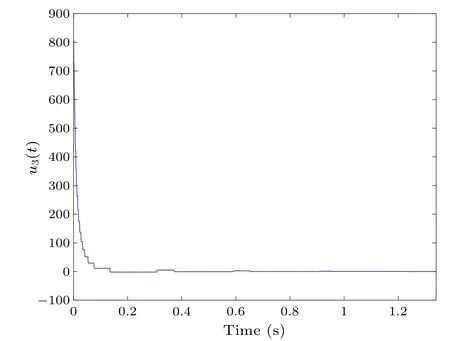
Fig.7.Control input evolution process for agent 3.
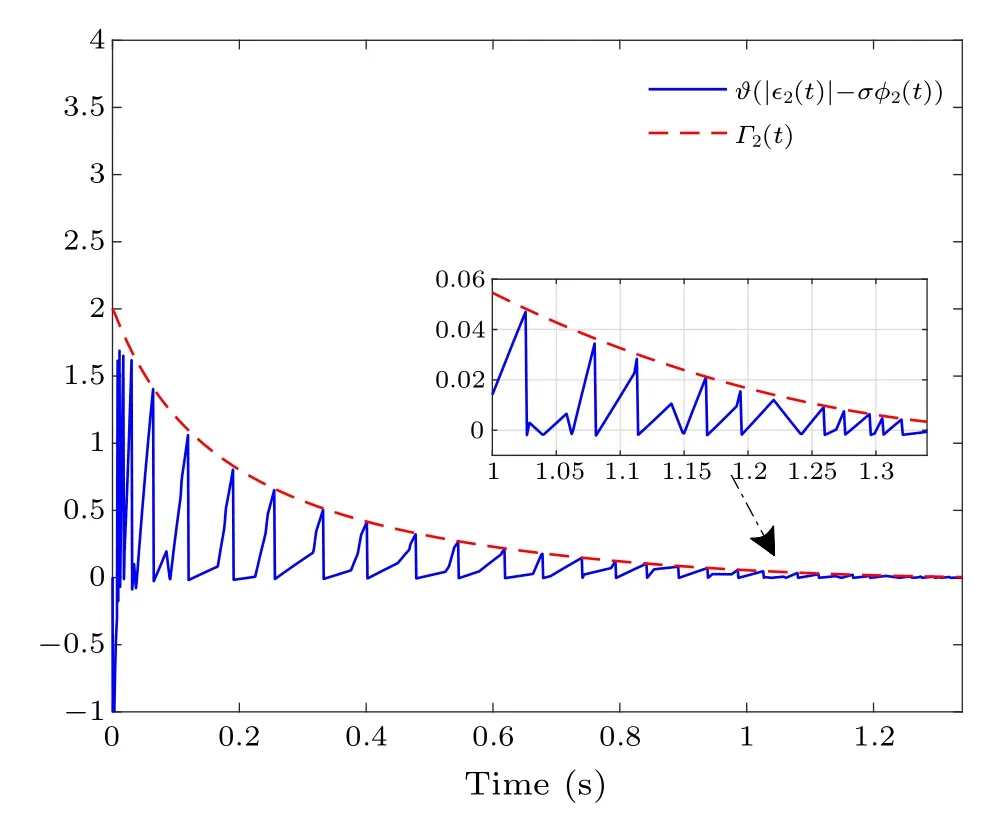
Fig.8.Evolution of ?(|ε2(t)|-σφ2(t))and Γ2(t).
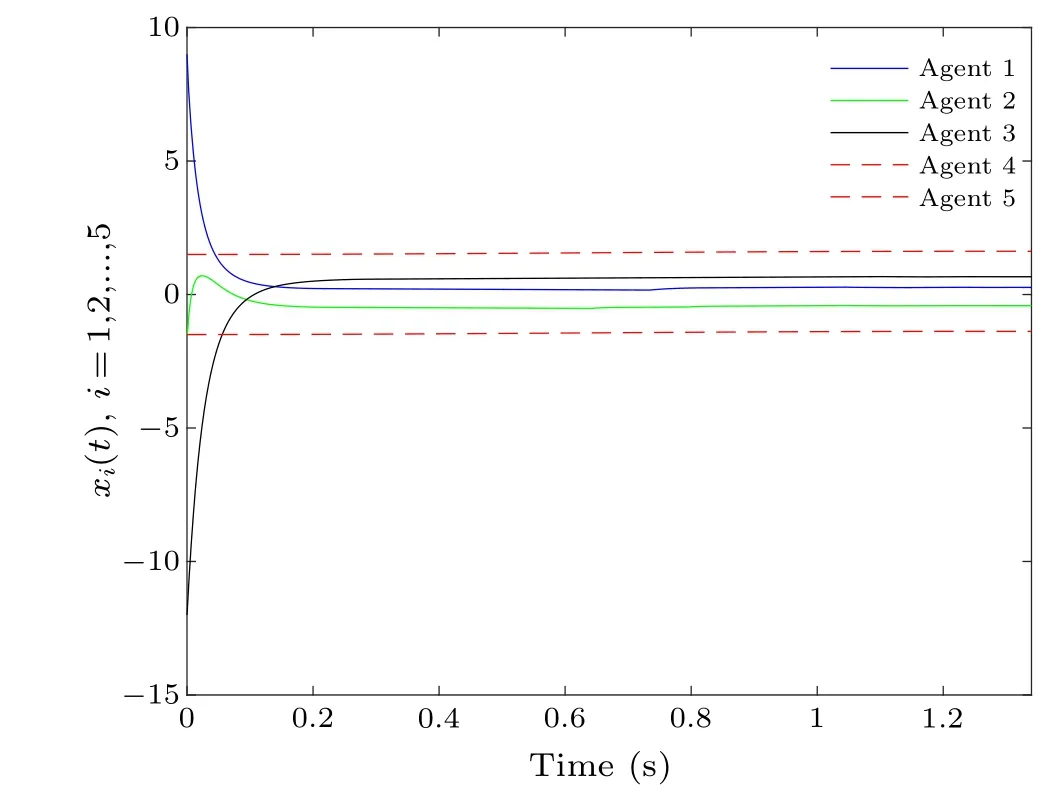
Fig.9.Process of state change under the team-triggered mechanism.
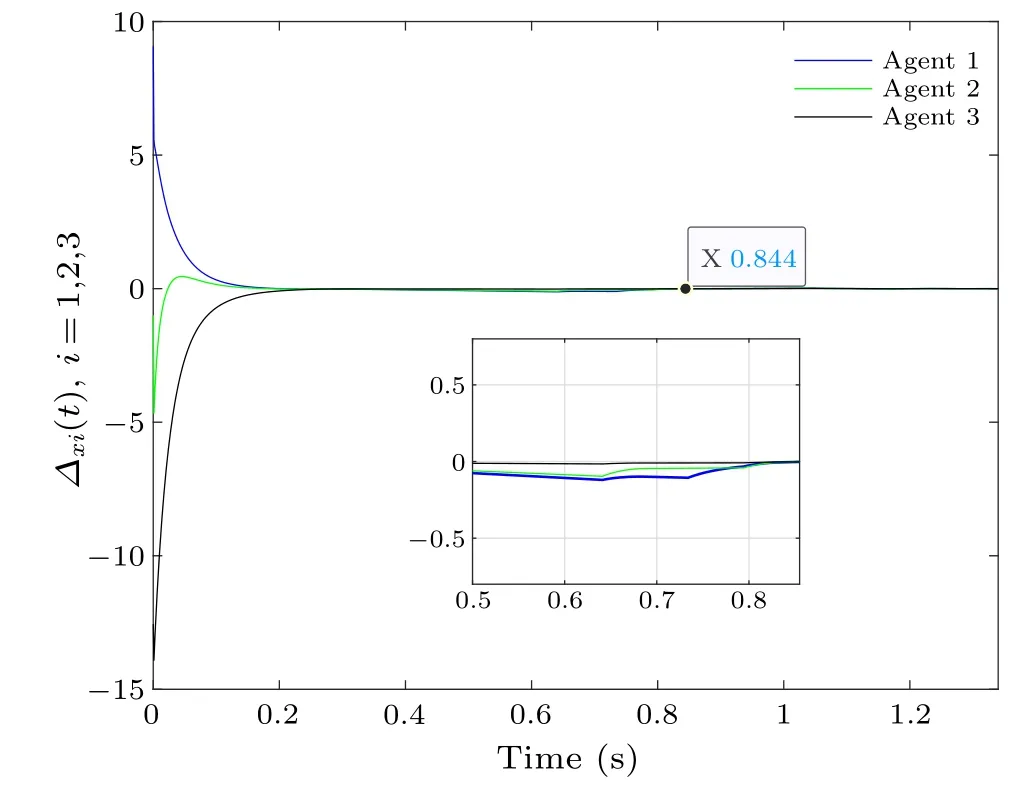
Fig.10.Team-based containment error.
Figure 11 shows the trigger moments for each agent and counts them in Table 1, implying that Zeno behavior is excluded, in addition we find that more triggers are needed to compare to Example 1, which confirms Remark 10 such that in a team-based triggering mechanism, more triggers are needed to compensate for the effects of discontinuous communication,but faster convergence can be obtained,therefore team-based triggering strategy makes a trade-off among convergence speed,communication cost and trigger time.
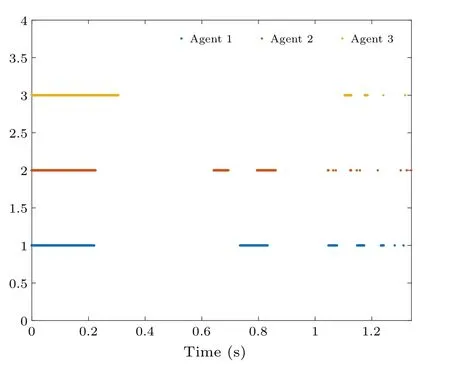
Fig.11.Trigger moments for team-based agents.

Table 1.Comparison of data under different trigger conditions.
Example 3 (Fixed time stability analysis) Containment control under DETC mechanism.
Assumed thatx(0) = [6;-2;-8;1;-1] andΓ(0) =[10;2;3], the state trajectories, containment errors, and agent trigger moments for all agents in the DETC condition(10)are shown in Figs.12-14,respectively.It is clear that the convergence time does not change with the initial condition of the agent despite its change,which achieves a fixed time containment control under the DETC condition(10).
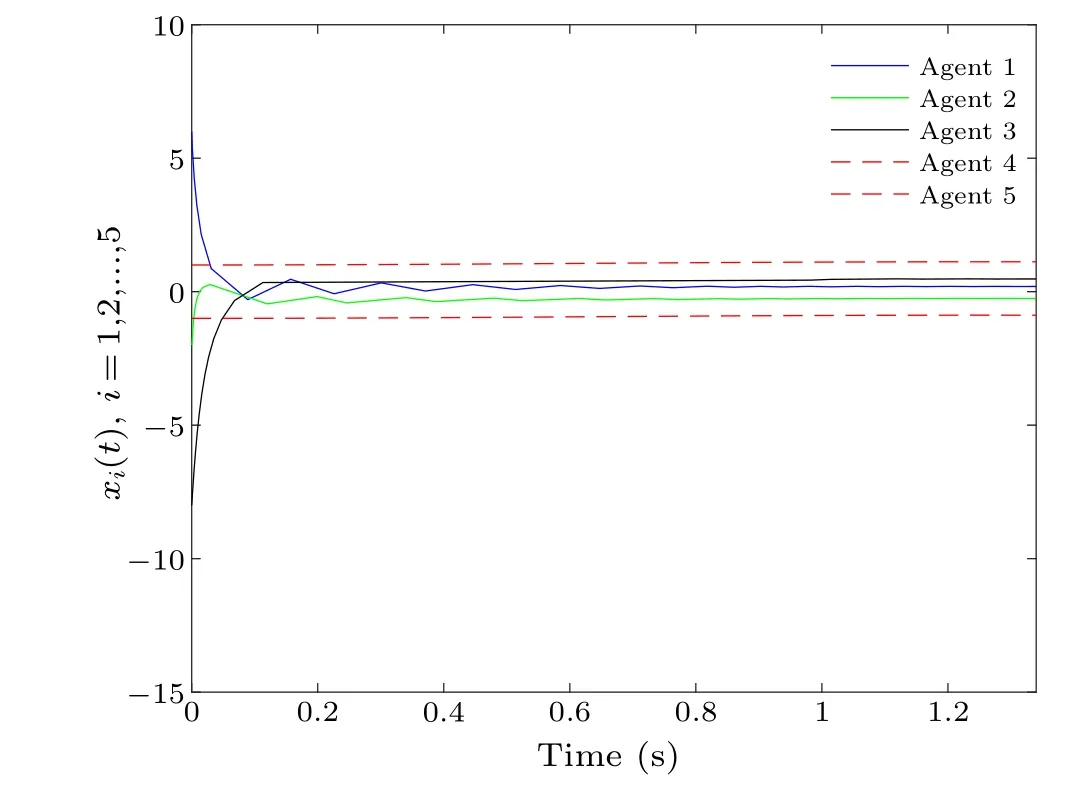
Fig.12.Process of state change under the DETC mechanism.
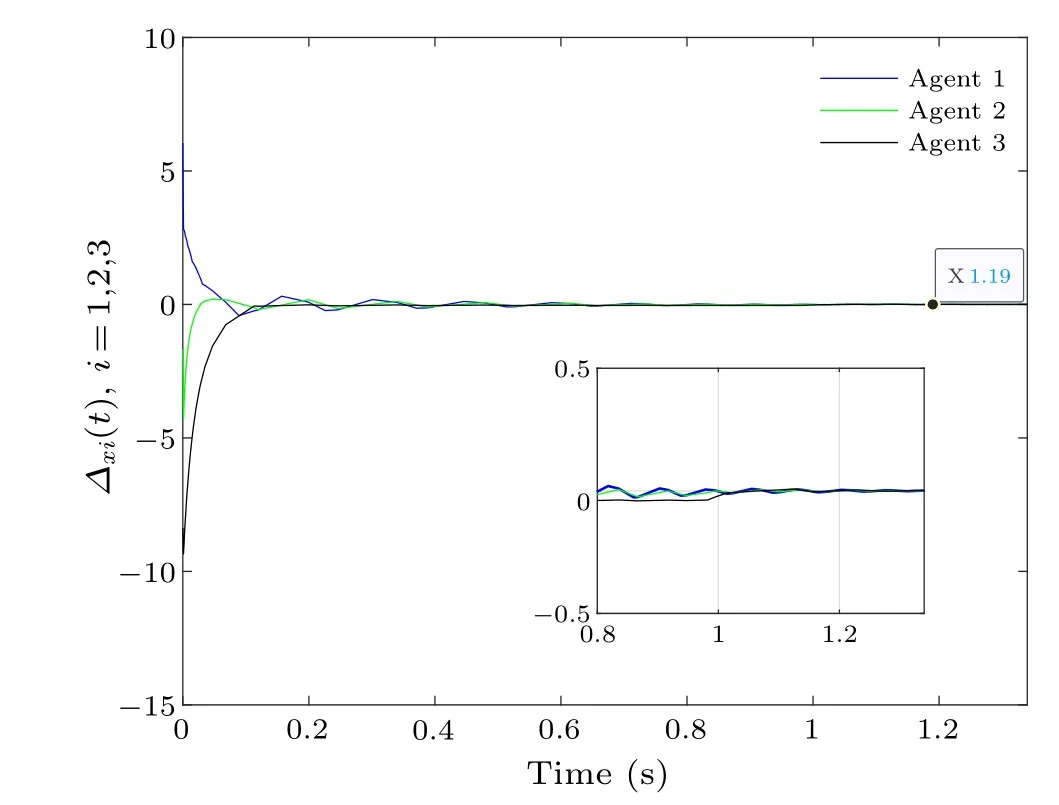
Fig.13.DETC-based containment error.
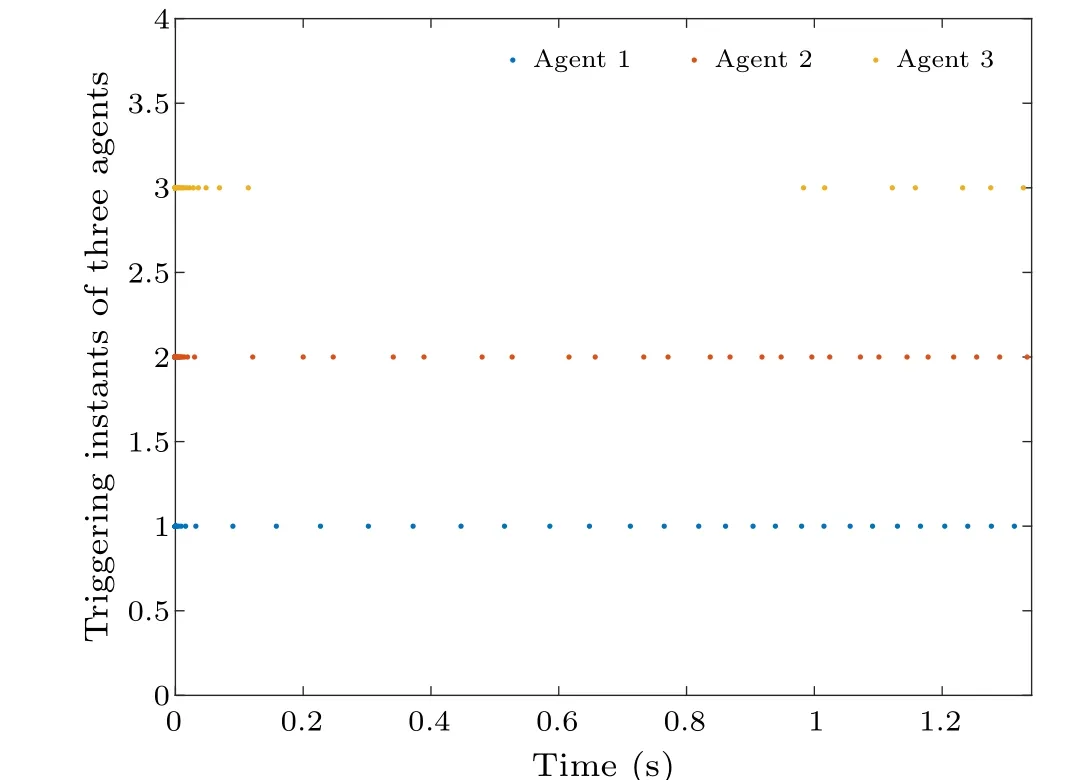
Fig.14.Trigger moments for DETC-based agents.
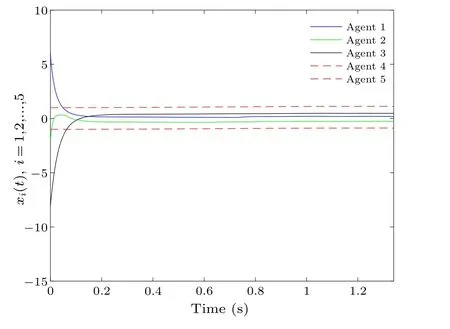
Fig.15.Process of state change under the team-triggered mechanism.
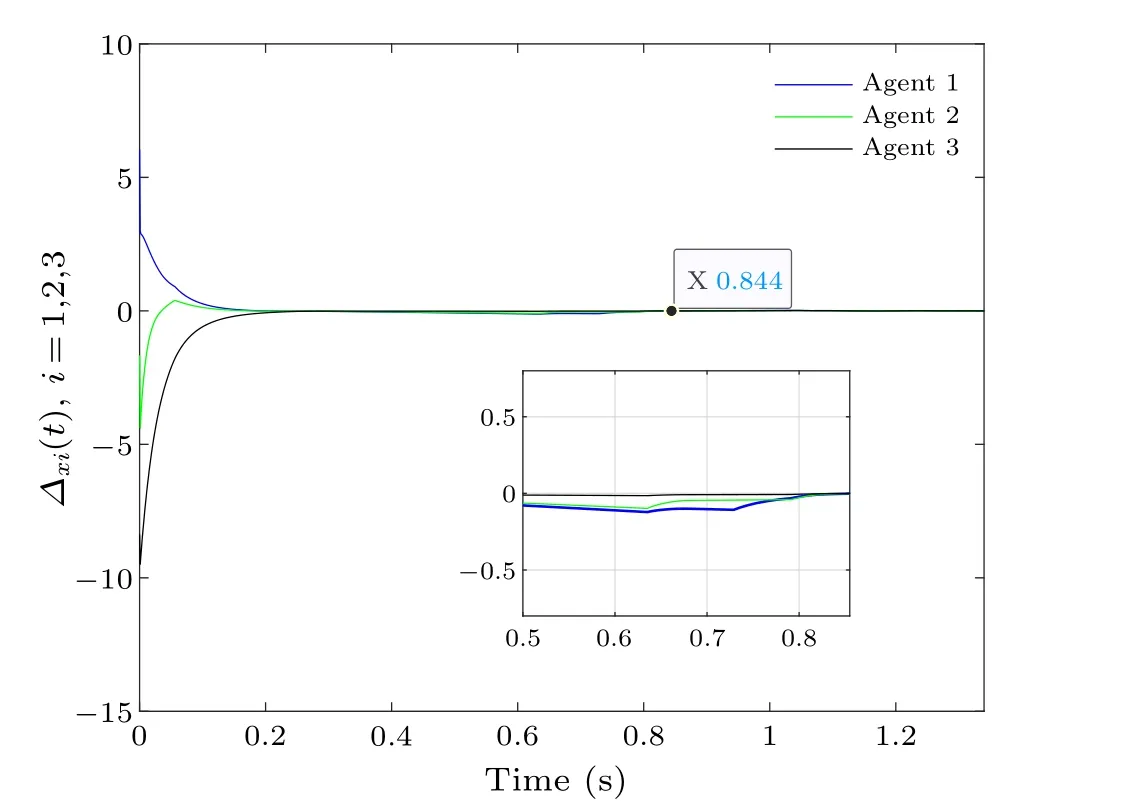
Fig.16.DETC-based containment error.
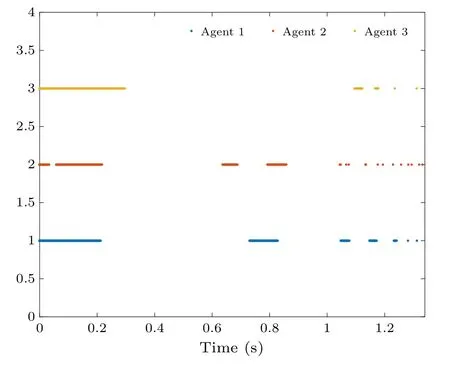
Fig.17.Trigger moments for team-based agents.
Example 4 (Fixed time stability analysis) Containment control under team-triggered mechanism.
Assumed thatx(0) = [6;-2;-8;1;-1] andΓ(0) =[10;2;3], similar to Example 3, we also give the state change process and trigger points under the team trigger conditions(44)as shown in Figs.15-17.Despite the change in the initial state,the final convergence time is the same as that of Example 2.
5.Conclusions
In summary,we have studied the fixed-time containment control problem with disturbances.Two different event triggering algorithms have been proposed to achieve fixed time containment control.The first algorithm successfully implements fixed-time containment control by designing a dynamic variable that reduces the number of controller updates, inspired by the application of dynamic event triggering techniques in consensus control.In order to overcome the problem of continuous communication, a team triggering mechanism has been further proposed, by combining the selftriggering strategy with the dynamic event method proposed in the first algorithm.Team-based triggering mechanisms have been shown to provide a trade-off among convergence time, communication cost, and number of triggers with limited time to achieve containment control, which can also be demonstrated by simulation.In the near future, we will further consider designing a dynamic self-triggering algorithm to achieve fixed-time containment control, where dynamic variables become directly part of the control of the self-triggering algorithm.It is interesting not only to completely eliminate continuous communication but also to reduce the number of triggers.In addition, it is of great potential for solving problems encountered in engineering fields (e.g., heterogeneous network system coordination problems,[34]input-output stability of switching systems).
Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant Nos.62173121, 62002095,61961019,and 61803139)and the Youth Key Project of Natural Science Foundation of Jiangxi Province of China (Grant No.20202ACBL212003).
- Chinese Physics B的其它文章
- Diamond growth in a high temperature and high pressure Fe-Ni-C-Si system: Effect of synthesis pressure
- Si-Ge based vertical tunnel field-effect transistor of junction-less structure with improved sensitivity using dielectric modulation for biosensing applications
- Speeding-up direct implicit particle-in-cell simulations in bounded plasma by obtaining future electric field through explicitly propulsion of particles
- Temperature-induced logical resonance in the Hodgkin-Huxley neuron
- Energy-distributable waterborne acoustic launcher for directional sensing
- Structural stability and ion migration of Li2MnO3 cathode material under high pressures

