周長最短與面積最小的Evans三角形
吳 波 (郵編:401249)
Guy在文獻(xiàn)[1]中引述了Evans于1977年提出的如下問題:
問題(Evans問題)[1]求出底能整除(這條底邊上的)高的一切整邊三角形.
將滿足“底能整除(這條底邊上的)高”的整邊三角形叫作Evans三角形.而此時的底邊叫做Evans邊,高與此底邊之比叫做Evans比.如果一個Evans三角形的三邊長是互素的,就叫作本原Evans三角形.
Evans問題雖然尚未完全解決,但國內(nèi)研究者已經(jīng)取得到了不少成果,相關(guān)文獻(xiàn)可以參閱文獻(xiàn)[2-5].
本文擬確定出周長最短與面積最小的Evans三角形,要用到如下結(jié)論:
結(jié)論1[1]Evans比不可能是1和2,但可以是3.
結(jié)論2[6]整邊直角三角形一定不是Evans三角形.
結(jié)論3[6]有兩邊相等的整邊三角形一定不是Evans三角形.
結(jié)論4[2]Evans三角形必定是Heron三角形.
結(jié)論5[7]本原海倫三角形的最小邊長是3,即不存在邊長是1或2的本原海倫三角形.
還要證明如下:
引理1若Heron三角形ABC的高CD為整數(shù),則△ACD,△BCD都是勾股三角形.
注勾股三角形即是整邊直角三角形.
證明(1)若Heron三角形ABC中a=b,由文獻(xiàn)[8]中等腰的本原海倫數(shù)組公式可知:此時△ACD,△BCD是兩個全等的勾股三角形.此時結(jié)論顯然成立.
(2)若Heron三角形ABC任兩邊不等,如圖1或圖2.
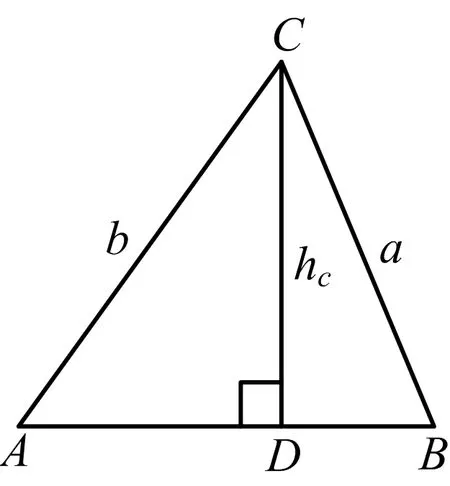
圖1
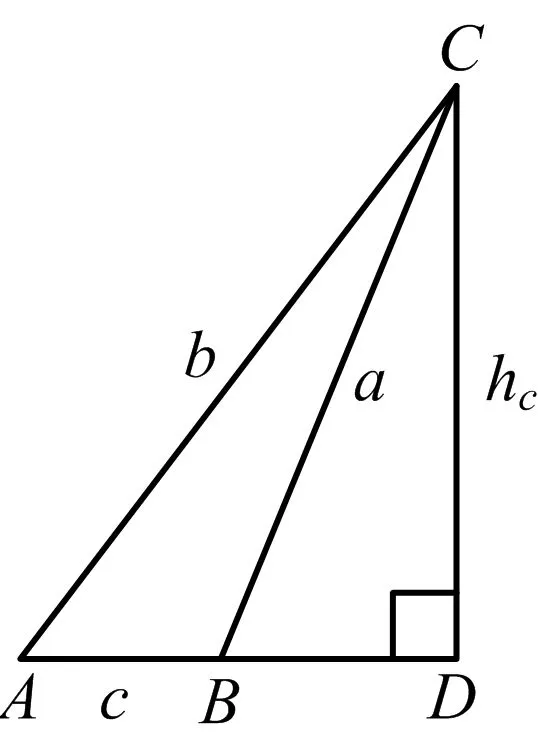
圖2
因Heron三角形三邊均為整數(shù),由余弦定理可知:cosA,cosB必為有理數(shù).結(jié)合圖1和圖2,由|AD|=b|cosA|,|BD|=a|cosB|知:|AD|,|BD|必為有理數(shù).
而題設(shè)中高CD也為整數(shù),由勾股定理并結(jié)合“|AD|,|BD|為有理數(shù)”可知:|AD|,|BD|必為整數(shù).因此△ACD,△BCD都是勾股三角形.證畢.
引理2若周長最短(面積最小)的Evans三角形ABC的Evans邊為c,則A,B中必有一個是鈍角.
證明對以c為Evans邊的周長最短(面積最小)的Evans三角形ABC,假設(shè)A,B都不是鈍角,又由結(jié)論2知:A,B不可能是直角,則A,B都是銳角,這表明:如圖1所示,c邊上的高h(yuǎn)c必在△ABC內(nèi).
Evans三角形為整邊三角形,結(jié)合Evans三角形定義可知:Evans邊c上的高h(yuǎn)c必為整數(shù).又由結(jié)論4知:Evans三角形必定是Heron三角形.再結(jié)合引理1可知:△ACD,△BCD都是勾股三角形.
勾股三角形顯然是Heron三角形.這樣,由結(jié)論5知:|AD|,|BD|中有一個至少為3,另一個至少為4(注意結(jié)論3表明:|AD|≠|(zhì)BD|).因此c=|AD|+|BD|≥7.
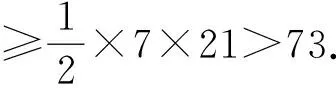
此時△ABC的周長>21+21+7=49.
但我們知道:存在周長小于49且面積小于73的Evans三角形.具體地說,在△ABC中a=13,b=15,c=4.易算得c邊上的高h(yuǎn)c=12.可以驗(yàn)證它是一個以c為Evans邊的Evans三角形.其周長為32<49,面積為24<73.
此Evans三角形的存在與引理2題設(shè)中的“最小”相矛盾.矛盾表明:假設(shè)不成立.所以A,B中必有一個是鈍角.證畢.
定理1周長最短與面積最小的Evans三角形都唯一存在,其Evans邊的長為4,另兩邊長分別為15,13.其周長為32,面積為24.
證明設(shè)周長最短與面積最小的Evans三角形ABC的Evans邊為c,c邊上的高CD記作hc.由引理2可知:a,b在高CD的同側(cè).如圖2,不妨設(shè)a 由結(jié)論5知:Evans邊c最小為3.下面我們分類討論. (1)若c=4,而結(jié)論1表明:Evans比最小為3. 若Evans比為3.則hc=3c=12.如圖2有: 由結(jié)論4和引理1知:△ACD,△BCD都是勾股三角形.因此a,b,|AD|,|BD|都是正整數(shù).用因式分解法很容易知道上述方程組有且僅有一組正整數(shù)解:a=13,|BD|=5,b=15,|AD|=9,c=4. 這個Evans三角形ABC的周長為32,面積為24. 由勾股定理可知:a>hc=16,b>hc=16. 此時△ABC的周長>16+16+4>32. 此時其周長及面積均大于前述那個Evans三角形. 這表明:此種情形下,其周長不是最短的,面積也不是最小的. 由勾股定理可知:a>hc=15,b>hc=15. 此時△ABC的周長>15+15+5>32. 顯然周長及面積均大于前述那個Evans三角形. 這表明:在此種情形下,其周長不是最短的,面積也不是最小的. (3)若c=3,而結(jié)論1表明:Evans比最小為3. 若Evans比為3.則hc=3c=9.如圖2有: |AD|-|BD|=c=3. 用因式分解法很容易知道上面第一個方程組有且僅有一個正整數(shù)解:a=15,|BD|=12,b=41,|AD|=40.但它們并不滿足第二個方程:|AD|-|BD|=c=3. 這表明:c=3,hc=9且a,b在高CD的同側(cè)的Evans三角形并不存在. 若Evans比為4.則hc=4c=12.如圖2,由勾股定理有: |AD|-|BD|=c=4. 同理可證:此方程組無正整數(shù)解. 這表明:c=3,hc=12且a,b在高CD的同側(cè)的Evans三角形并不存在. 若Evans比為5.則hc=5c=15.如圖2,由勾股定理有: |AD|-|BD|=c=5. 同理可證:此方程組無正整數(shù)解. 這表明:c=3,hc=15且a,b在高CD的同側(cè)的Evans三角形并不存在. 由勾股定理可知:a>hc=18,b>hc=18. 此時△ABC的周長>18+18+3>32. 顯然周長及面積均大于前述那個Evans三角形. 這表明:此種情形下,其周長不是最短的,面積也不是最小的. 綜上可知:三邊長分別為15,13,4的三角形就是周長最短的Evans三角形,同時它也是面積最小的Evans三角形.證畢. 引理2中證明了周長最短(面積最小)的Evans三角形必定是鈍角三角形.其實(shí),文獻(xiàn)[6]中有一個一般性的 猜想[6]Evans三角形必定是鈍角三角形. 需要說明的是:文獻(xiàn)[9]曾經(jīng)對上述猜想給出過一個“證明”,但這個“證明”并不正確.因?yàn)槲墨I(xiàn)[9]中的證明依賴于文獻(xiàn)[10]中的“充要條件”,而我們已經(jīng)發(fā)現(xiàn)并給出了具體的反例說明:文獻(xiàn)[10]中的“充要條件”是錯誤的.在文獻(xiàn)[10]中的“充要條件”的基礎(chǔ)上進(jìn)行推導(dǎo)的文獻(xiàn)[9]和文獻(xiàn)[11]中的結(jié)論大多并不成立.相關(guān)結(jié)果將另外撰文予以說明. 因此,對上述猜想有興趣的讀者可以繼續(xù)探討.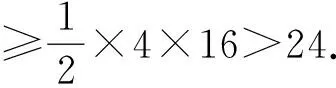
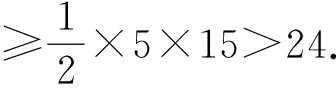
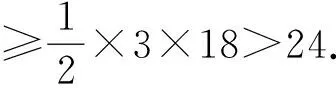
 中學(xué)數(shù)學(xué)教學(xué)2023年5期
中學(xué)數(shù)學(xué)教學(xué)2023年5期
- 中學(xué)數(shù)學(xué)教學(xué)的其它文章
- 智慧課堂優(yōu)化高三藝術(shù)生數(shù)學(xué)復(fù)習(xí)的有效探究
- 智慧學(xué)習(xí)環(huán)境下初中數(shù)學(xué)原理課教學(xué)實(shí)踐與思考
——以滬科版數(shù)學(xué)“勾股定理”為例 - 大道至簡:復(fù)習(xí)課教學(xué)的應(yīng)然追求
- 涵蓋全面 重視基礎(chǔ) 兼顧發(fā)展
——2023年安徽中考第22題印象 - 素養(yǎng)觀下尺規(guī)作圖教學(xué)的思考
- 立足素養(yǎng)重思維 減負(fù)提質(zhì)重基礎(chǔ)
——2023年安徽省中考數(shù)學(xué)試卷評析
