姜 曼

(西安交通工程學(xué)院 公共課部,陜西 西安 710300)

繼Zadeh[1]提出模糊集概念后,近年來(lái),模糊集及其擴(kuò)展為處理不同問(wèn)題的不確定性提供了思路與方法,人們對(duì)模糊集的研究熱情迅速增長(zhǎng),直覺(jué)模糊集于1983年由Atanassov[2]提出,區(qū)間值模糊集是由Sambuc[3]首先研究的,他將其稱(chēng)為φ-flou函數(shù),用于捕捉不確定性的特征.Torra[4]提出了猶豫模糊集并且證明了猶豫模糊集的包絡(luò)是直覺(jué)模糊集,此外在應(yīng)用于猶豫模糊集的包絡(luò)時(shí),他們提出的關(guān)于猶豫模糊集的操作與初始模糊集的操作是一致的.

古典邏輯是絕對(duì)性和相對(duì)性的統(tǒng)一,是一切知識(shí)的基礎(chǔ),是人類(lèi)全面認(rèn)識(shí)的基本部分.演繹邏輯推理是二元邏輯,這意味著只有兩種選擇:真或假;另一方面,不確定性不僅僅是真是假,它也可能有多種結(jié)果.不確定性推理是人工智能研究的一個(gè)重要方面,在邏輯背景下對(duì)其進(jìn)行檢驗(yàn)是一種科學(xué)研究方法.Cao等[5]在他們的書(shū)中介紹了坡代數(shù)的概念,Kim和Roush[6]研究了坡代數(shù)的結(jié)構(gòu),Murali[7]討論了模糊等價(jià)關(guān)系,Ahn[8]研究了坡代數(shù)的永久性,Ahn和Kim[9]引入了坡代數(shù)中的R映射及L映射,研究它們之間的關(guān)系.近年來(lái),Kim[10]研究了f-坡代數(shù)的廣義右f-導(dǎo)子,Alshehri等[11-12]分別研究了坡代數(shù)的導(dǎo)子與廣義導(dǎo)子,王豐效[13-14]研究了反模糊子坡代數(shù)以及區(qū)間值模糊子坡代數(shù),這些研究對(duì)認(rèn)識(shí)坡代數(shù)有很強(qiáng)的理論意義.坡代數(shù)是邏輯代數(shù)的一個(gè)典型代表,它上面的準(zhǔn)則,比如濾子,子代數(shù),理想等都有很強(qiáng)的研究意義.因此,本文主要研究坡代數(shù)中的I-V猶豫模糊子坡代數(shù),得到了一些有意義的結(jié)果.

1 預(yù)備知識(shí)

定義1[4]設(shè)X非空,X上的猶豫模糊集F有如下定義:

F={:hF(x)∈ρ([0,1]),x∈X},

其中ρ([0,1])是[0,1]上的冪集. 記為F∈HF(X).

稱(chēng)集合X(F,γ):={x∈X|γ?hF(x)}為F的猶豫水平集,其中γ?P([0,1]).

定義2[4]對(duì)于F∈HF(X),猶豫模糊元hF(x)的下界和上界分別定義如下:

下界:hF-(x)=minhF(x); 上界:hF+(x)=maxhF(x).

設(shè)F,G∈HF(X),記F∩G為F和G的交集,且有如下定義:對(duì)?x∈X,

hF∩G(x)=hF(x)∩hG(x)={h∈hF(x)∩hG(x)|h≤min(hF+(x),hG+(x))}.

定義3[15]設(shè)X非空,對(duì)?x,y,z∈X,如果有

(1)x+y=y+x;

(2)(x+y)+z=x+(y+z);

(3)(x*y)*z=x*(y*z);

(4)(x*(y+z)=x*y+x*z;

(5)(y+z)*x=y*x+z*x;

(6)x+x=x;

(7)x+x*y=x;

(8)y+x*y=y.

則稱(chēng)(X,+,*)為坡代數(shù).以下均用X表示坡代數(shù).

引理1[15]設(shè)(X,+,*)和(Y,+,*)是兩個(gè)坡代數(shù). 在X×Y定義如下運(yùn)算:對(duì)?(x1,y1),(x2,y2)∈X×Y,規(guī)定(x1,y1)+(x2,y2)=(x1+x2,y1+y2),(x1,y1)*(x2,y2)=(x1*x2,y1*y2). 則X×Y關(guān)于上述運(yùn)算構(gòu)成一個(gè)坡代數(shù).

定義4[15]設(shè)(X,+,*)和(Y,+,*)是坡代數(shù),令f:X→Y,若對(duì)?x1,x2∈X,有f(x1+x2)=f(x1)+f(x2);f(x1*x2)=f(x1)*f(x2)成立,則稱(chēng)f:X→Y為從X到Y(jié)的同態(tài).

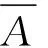
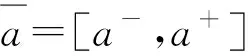
D1≥D2?a1≥b1,a2≥b2;D1=D2?a1=b1,a2=b2

γmin(D1,D2)=[min{a1,a2},min{b1,b2}]=[a1∧a2,b1∧b2]

γmax(D1,D2)=[max{a1,a2},max{b1,b2}]=[a1∨a2,b1∨b2]

定義6[17]非空集合X上的一個(gè)I-V模糊集定義為A={x,[μA-,μA+]|x∈X},其中μA-,μA+是兩個(gè)模糊集,且有μA-≤μA+,?x∈X,記A(x)=[μA-(x),μA+(x)],對(duì)?x∈X,A(x)∈D[0,1]表示X上的I-V模糊集.

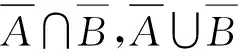
2 坡代數(shù)的I-V猶豫模糊子坡代數(shù)

定義8 設(shè)集合hA(x)={(x,[hμA-(x)hμA+(x)])|x∈X},其中hμA-(x)∈HF(X),hμA+(x)∈HF(X),且有hμA-(x)?hμA+(x),?x∈X.則稱(chēng)A是X上的一個(gè)I-V猶豫模糊集.記為A∈HFI(X).

定義9 設(shè)A∈HF(X),若對(duì)?x,y∈X,都有hA(x+y)∩hA(x*y)?hA(x)∩hA(y),則稱(chēng)A是X的猶豫模糊子坡代數(shù). 記為A∈HFS(X).

定義10 設(shè)A∈HFI(X),若對(duì)?x,y∈X,如果A滿足條件:

γmin(hA(x+y),hA(x*y))?γmin(hA(x),hA(y)),

則稱(chēng)A是X的I-V猶豫模糊子坡代數(shù). 記為A∈HFIS(X).

定理1A={(x,[hμA-(x),hμA+(x)])|x∈X}∈HFIS(X)當(dāng)且僅當(dāng)hμA-(x)∈HFS(X)且hμA+(x)∈HFS(X)成立.

證明必要性 若A∈HFIS(X),則對(duì)?x,y∈X,有:

γmin(hA(x+y),hA(x*y))?γmin(hA(x),hA(y)).所以有

γmin(hA(x+y),hA(x*y))=γmin([hμA-(x+y),hμA+(x+y)],[hμA-(x*y),hμA+(x*y)])

?γmin(hA(x),hA(y))

=γmin([hμA-(x),hμA+(x)],[hμA-(y),hμA+(y)])

=[hμA-(x)∩hμA-(y),hμA+(x)∩hμA+(y)],

由于γmin([hμA-(x+y),

hμA+(x+y)],[hμA-(x*y),hμA+(x*y)])

=[hμA-(x+y)∩hμA-(x*y),hμA+(x+y)∩hμA+(x*y)],

因此[hμA-(x+y)∩hμA-(x*y),hμA+(x+y)∩hμA+(x*y)]?[hμA-(x)∩hμA-(y),hμA+(x)∩hμA+(y)].

于是可得

hμA-(x+y)∩hμA-(x*y)?hμA-(x)∩hμA-(y),hμA+(x+y)∩hμA+(x*y)?hμA+(x)∩hμA+(y).

即hμA-(x)∈HFS(X)且hμA+(x)∈HFS(X).

充分性 已知hμA-(x)∈HFS(X)且hμA+(x)∈HFS(X).則對(duì)?x,y∈X,有

hμA-(x+y)∩hμA-(x*y)?hμA-(x)∩hμA-(y),hμA+(x+y)∩hμA+(x*y)?hμA+(x)∩hμA+(y).

因此有

[hμA-(x+y)∩hμA-(x*y),hμA+(x+y)∩hμA+(x*y)]?[hμA-(x)∩hμA-(y),hμA+(x)∩hμA+(y)],

γmin(hA(x),hA(y))=γmin([hμA-(x),hμA+(x)],

[hμA-(y),hμA+(y)])=[hμA-(x)∩hμA-(y),hμA+(x)∩hμA+(y)],

γmin(hA(x+y),hA(x*y))=γmin([hμA-(x+y),hμA+(x+y)],[hμA-(x*y),hμA+(x*y)])

=[hμA-(x+y)∩hμA-(x*y),hμA+(x+y)∩hμA+(x*y)]

所以,對(duì)?x,y∈X,有γmin(hA(x+y),hA(x*y))?γmin(hA(x),hA(y)). 即A∈HFIS(X).

定義11 設(shè)A∈HFI(X)和B∈HFI(X),定義I-V猶豫模糊集A∩B為:

(A∩B)(x)=γmin(A(x),B(x)),?x∈X

其中,hA∩B(x)=γmin(hA(x),hB(x)).

定理2 設(shè)A∈HFIS(X)和B∈HFIS(X),則A∩B∈HFIS(X).

證明設(shè)A∈HFIS(X)和B∈HFIS(X),則對(duì)?x,y∈X,有

γmin(hA(x+y),hA(x*y))?γmin(hA(x),hA(y)),

γmin(hB(x+y),hB(x*y))?γmin(hB(x),hB(y)),

于是

γmin(hA∩B(x+y),hA∩B(x*y))

=γmin(γmin(hA(x+y),hB(x+y)),γmin(hA(x*y),hB(x*y)))

=γmin(γmin(hA(x+y),hA(x*y)),γmin(hB(x+y),hB(x*y)))

?γmin(γmin(hA(x),hA(y)),γmin(hB(x),hB(y)))

=γmin(γmin(hA(x),hB(x)),γmin(hA(y),hB(y)))

=γmin(hA∩B(x),hA∩B(y)),

因此,A∩B∈HFIS(X).

3 坡代數(shù)的I-V猶豫模糊子坡代數(shù)的直積與同態(tài)像

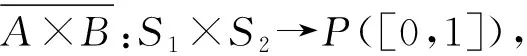
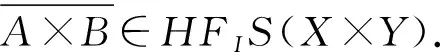
證明如果有A∈HFIS(X)和B∈HFIS(X),則對(duì)?(x1,y1),(x2,y2)∈X×Y,可得

γmin(hA(x1+x2),hA(x1*x2))?γmin(hA(x1),hA(x2)),

γmin(hB(y1+y2),hB(y1*y2))?γmin(hB(y1),hB(y2)),

因此有:

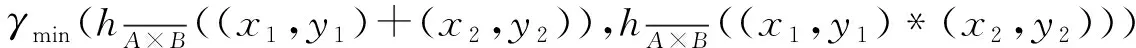
=γmin(γmin(hA(x1+x2),hB(y1+y2)),γmin(hA(x1*x2),hB(y1*y2))

?γmin(γmin(hA(x1),hA(x2)),γmin(hB(y1),hB(y2)))

=γmin(γmin(hA(x1),hB(y1)),γmin(hA(x2),hB(y2)))

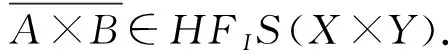
定理4 設(shè)f:X→Y為同態(tài)滿射,若A∈HFIS(X),則f(A)∈HFIS(Y). 且有hf(A)(y)=γmin(hA(x)|f(x)=y).

證明因?yàn)閒:X→Y為同態(tài)滿射,則對(duì)?y1,y2∈Y,?x1,x2∈X,我們有f(x1)=y1,f(x2)=y2. 因此

hf(A)(y1+y2)=γmin{hA(x)|f(x)=y1+y2}

=γmin{hA(x1+x2)|f(x1+x2)=y1+y2}

=γmin{(hA(x1+x2)|f(x1)+f(x2)=y1+y2)},

hf(A)(y1*y2)=γmin{hA(x)|f(x)=y1*y2}

=γmin{hA(x1*x2)|f(x1*x2)=y1*y2}

=γmin{(hA(x1*x2)|f(x1)*f(x2)=y1*y2)},

由于A∈HFIS(X),即對(duì)x1,x2∈X,有

γmin(hA(x1+x2),hA(x1*x2))?γmin(hA(x1),hA(x2)),

γmin(hf(A)(y1+y2),hf(A)(y1*y2))

=γmin(γmin{hA(x1+x2)|f(x1)+f(x2)=y1+y2},γmin{hA(x1*x2)|f(x1)*f(x2)=y1*y2})

=γmin(γmin(hA(x1+x2),hA(x1*x2))|f(x1)+f(x2)=y1+y2,f(x1)*f(x2)=y1*y2)

?γmin(γmin(hA(x1),hA(x2))|f(x1)+f(x2)=y1+y2,f(x1)*f(x2)=y1*y2)

=γmin(γmin(hA(x1),hA(x2))|f(x1)=y1,f(x2)=y2)

=γmin(γmin{hA(x1)|f(x1)=y1},γmin{hA(x2)|f(x2)=y2})

=γmin(hf(A)(y1),hf(A)(y2)),

所以,f(A)∈HFIS(Y).

4 結(jié)論

對(duì)于坡代數(shù)的研究,濾子和理想是一個(gè)重要的研究?jī)?nèi)容,本文在坡代數(shù)中研究了I-V猶豫模糊子坡代數(shù),豐富了坡代數(shù)和猶豫模糊集的理論研究,類(lèi)似的研究思路與方法,也可用于研究BE-代數(shù),BL-代數(shù)和MV-代數(shù)等.