曹 穎,楊 海,羅永亮

(西安工程大學(xué) 理學(xué)院,陜西 西安 710048)

1 介紹

Smarandache函數(shù)是由數(shù)論專家Smarandache教授提出的一個(gè)非常重要的數(shù)論函數(shù)[1].后來,數(shù)論學(xué)家通過與Smarandache函數(shù)的類比,定義了偽Smarandache函數(shù)和Smarandache LCM函數(shù).對(duì)于任意的正整數(shù)n,偽Smarandache函數(shù)Z(n)定義為滿足條件的最小的正整數(shù)m[2],即

對(duì)于任意的正整數(shù)n,Smarandache LCM函數(shù)SL(n)定義為滿足條件的最小的正整數(shù)m[3],即

SL(n)=min{m:m∈Z+,n|lcm[1,2,3,…,m]}.

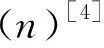
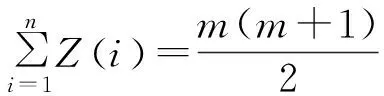
本文進(jìn)一步對(duì)相關(guān)數(shù)論函數(shù)方程可解性問題進(jìn)行研究,利用初等方法和Z(n),SL(n),φe(n)的基本性質(zhì),討論了當(dāng)e=1,2,3,4時(shí),數(shù)論函數(shù)方程

Z(SL(n))=φe(n)

的可解性,得到了如下主要結(jié)果.

設(shè)n=2kp1k1p2k2…psks,其中p1,p2,…,ps都是素?cái)?shù),s,k1,k2,…,ks∈N.

定理1.1 若e=1,則方程Z(SL(n))=φ(n)的所有正整數(shù)解是n=1或n=2ps,其中psks=max{2k,p1k1,p2k2,…,psks},ks=1.

定理1.2 若e=2,則方程Z(SL(n))=φ2(n)的所有正整數(shù)解為n=4ps,其中psks=max{2k,p1k1,p2k2,…,psks},ks=1.

定理1.3 如果e=3,那么除了方程Z(SL(n))=φ3(n)的正整數(shù)解n=72外,存在其他正整數(shù)解的必要條件是ps=2t+1(t∈N,1≤t≤s,psks=max{2k,p1k1,p2k2,…,psks},pi≡2(mod3)(1≤i≤s),3α∈{p1k1,p2k2,…,psks,1},α∈{0,1}).

定理1.4 若e=4,則方程Z(SL(n))=φ4(n)的正整數(shù)解為n=8ps,其中psks=max{2k,p1k1,p2k2,…,psks},且pi≡3(mod4)(1≤i≤s)和k=0,1不同時(shí)成立.存在其他正整數(shù)解的必要條件是ps=2t+1,(t∈N,1≤t≤s+1,psks=max{2k,p1k1,p2k2,…,psks},k=1,pi≡3(mod4)(1≤i≤s))或ps=2t+1(t∈N,1≤t≤s+2,psks=max{2k,p1k1,p2k2,…,psks},k=0,pi≡3(mod4)(1≤i≤s)).

2 引理

為了完成定理的證明,我們需要以下幾個(gè)簡(jiǎn)單引理.

引理2.1[13]對(duì)于任意素?cái)?shù)p,φ(pk)=pk-pk-1(k∈N*).

引理2.2[13]令正整數(shù)n標(biāo)準(zhǔn)分解為n=2kp1k1p2k2…psks,其中p1,p2,…,ps為不同的奇素?cái)?shù),且s,k1,k2,…,ks∈N,則有SL(n)=max{2k,p1k1,p2k2,…,psks}.

引理2.3[13]對(duì)于任意奇素?cái)?shù)p≥3及k≥1,有Z(pk)=pk-1(k∈N*),當(dāng)p=2時(shí),則有Z(2k)=2k+1-1(k∈N).

引理2.4[6]設(shè)n=3αp1k1p2k2…psks為任意正整數(shù),其中p1,p2,…,ps是除3和α,s,k1,k2,…,ks∈N之外的不同素?cái)?shù),則

引理2.5[6]設(shè)n=2αp1k1p2k2…psks為任意正整數(shù),其中p1,p2,…,ps為不同的奇素?cái)?shù),且α,s,k1,k2,…,ks∈N,則

3 定理的證明

定理1.1的證明令n=2kp1k1p2k2…psks,其中p1,p2,…,ps都是素?cái)?shù),s,k1,k2,…,ks∈N,在以下三種情況下討論方程Z(SL(n))=φe(n)(e=1)的解:

(i) 顯然,Z(SL(1))=φ(1),因此n=1是方程Z(SL(n))=φ(n)的解.

(ii) 若2k=max{2k,p1k1,p2k2,…,psks},則k≥1.在這種情況下,由引理2.2可得SL(n)=2k,又由引理2.3可得Z(SL(n))=2k+1-1.將Z(SL(n))=2k+1-1和φ(n)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)代入方程Z(SL(n))=φ(n)可得

2k+1-1=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),

求解此方程可得k=1,n=2,即3=p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),顯然不成立,所以方程Z(SL(n))=φ(n)在這種情況下無解.

(iii) 若psks=max{2k,p1k1,p2k2,…,psks},則k≥1.在這種情況下,由引理2.2可得SL(n)=psks,又由引理2.3可得Z(SL(n))=psks-1.將Z(SL(n))=psks-1和φ(n)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)代入方程Z(SL(n))=φ(n)可得

psks-1=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),

求解此方程可得ks=1,k=1,n=2ps,所以方程Z(SL(n))=φ(n)在這種情況下有解n=2ps.

綜上所述,定理1.1結(jié)論成立.

定理1.2的證明令n=2kp1k1p2k2…psks,其中p1,p2,…,ps都是素?cái)?shù),s,k1,k2,…,ks∈N,在以下三種情況下討論方程Z(SL(n))=φe(n)(e=2)的解:

(i) 顯然,Z(SL(1))≠φ2(1),Z(SL(2))≠φ2(2),因此n=1,2不是方程Z(SL(n))=φ2(n)的解.

(ii) 若2k=max{2k,p1k1,p2k2,…,psks},則k≥2.在這種情況下,由引理2.2可得SL(n)=2k,又由引理2.3可得Z(SL(n))=2k+1-1.將Z(SL(n))=2k+1-1和φ2(n)=2k-2p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)代入方程Z(SL(n))=φ2(n)可得

2k+1-1=2k-2p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),

方程右邊是奇數(shù),易知k=2.進(jìn)一步可得,7=p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),顯然,這個(gè)方程不成立,此時(shí)方程Z(SL(n))=φ2(n)無解.

(iii) 設(shè)psks=max{2k,p1k1,p2k2,…,psks},則k≥1.在這種情況下,由引理2.2可得SL(n)=psks,又由引理2.3可得Z(SL(n))=psks-1.將Z(SL(n))=psks-1和φ2(n)=2k-2p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)代入方程Z(SL(n))=φ2(n)可得

psks-1=2k-2p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1),

對(duì)此方程兩端同時(shí)取模ps,則psks-1≡-1≡-2k-2p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(modps),易得ks=1,k=2,n=4ps,此時(shí)方程Z(SL(n))=φ2(n)有解n=4ps.

綜上所述,定理1.2結(jié)論成立.

定理1.3的證明令n=2kp1k1p2k2…psks,其中p1,p2,…,ps都是素?cái)?shù),s,k1,k2,…,ks∈N,在以下三種情況下討論方程Z(SL(n))=φe(n)(e=3)的解:

(i) 顯然,Z(SL(1))≠φ3(1),Z(SL(2))≠φ3(2),Z(SL(3))≠φ3(3),即n=1,2,3不是方程Z(SL(n))=φ3(n)的解.

(ii) 若2k=max{2k,p1k1,p2k2,…,psks},則k≥2.在這種情況下,由引理2.2可得SL(n)=2k,又由引理2.3可得Z(SL(n))=2k+1-1.

分兩種情況進(jìn)行討論:

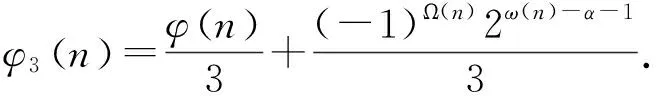
代入方程Z(SL(n))=φ3(n)可得

3(2k+1-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2ω(n)-α-1.

在以下兩種情形下討論α:

當(dāng)α=0時(shí),如果ω(n)=1,則n=2k,由上式進(jìn)一步可得3(2k+1-1)=2k-1+(-1)Ω(n)=2k-1+(-1)k,即11×2k-1=3+(-1)k.顯然,此方程不成立.若ω(n)>1,方程左邊是奇數(shù),右邊是偶數(shù),不可能成立.因此在這種情形下,方程Z(SL(n))=φ3(n)無解.

當(dāng)α=1時(shí),ω(n)≥2.若ω(n)=2,則n=2k×3.對(duì)方程3(2k+1-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2ω(n)-α-1兩邊取模3可得0≡(-1)Ω(n)22-1-1≡(-1)Ω(n)(mod3),顯然這個(gè)同余公式不成立;若ω(n)>2,且k≥2,方程左邊是奇數(shù),右邊是偶數(shù),不可能成立.因此在這種情形下,方程Z(SL(n))=φ3(n)無解.

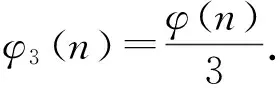
(iii) 若psks=max{2k,p1k1,p2k2,…,psks},則k≥1.在這種情況下,由引理2.2可得SL(n)=psks,又由引理2.3可得Z(SL(n))=psks-1.

分兩種情況進(jìn)行討論:

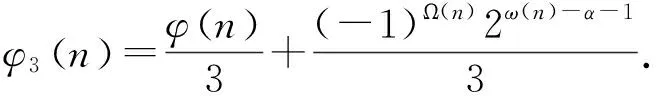
代入方程Z(SL(n))=φ3(n)可得

3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2ω(n)-α-1.

在以下兩種情形下討論α:

當(dāng)α=0時(shí),若ω(n)=s+1,由上式進(jìn)一步可得3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2s.對(duì)方程兩邊同時(shí)取模ps-1可得0≡(-1)Ω(n)2s≡2s(modps-1),因此ps=2t+1(t∈N,1≤t≤s)是方程有解的必要條件.根據(jù)初等數(shù)論知識(shí),若ps=2t+1是一個(gè)素?cái)?shù),則p是2的平方,所以ps是費(fèi)馬素?cái)?shù).到目前為止,只發(fā)現(xiàn)了5個(gè)費(fèi)馬素?cái)?shù).如果費(fèi)馬素?cái)?shù)只存在有限個(gè)的假設(shè)成立,那么方程Z(SL(n))=φ3(n)在這種情形下只存在有限個(gè)解.

當(dāng)α=1時(shí),ω(n)≥2.若ω(n)=2,則n=2k×3.對(duì)方程3(2k+1-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2ω(n)-α-1兩邊取模3可得0≡(-1)Ω(n)22-1-1≡(-1)Ω(n)(mod3),顯然這個(gè)同余公式不成立;若ω(n)>2,根據(jù)k≥2,方程左邊是奇數(shù),右邊是偶數(shù),不可能成立.因此在這種情形下,方程Z(SL(n))=φ3(n)無解.

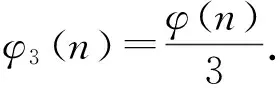
代入方程Z(SL(n))=φ3(n)可得3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1).

在以下兩種情形下討論ks:

當(dāng)ks=1時(shí),若ω(n)=s+1,由上式進(jìn)一步可得3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…ps-1ks-1-1(ps-1-1).顯然,方程左邊是奇數(shù)且右邊是偶數(shù),不可能成立.因此在這種情形下,方程Z(SL(n))=φ3(n)無解.

當(dāng)ks>1時(shí),對(duì)方程3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)兩邊取模ps可得-3≡0(modps),易得ps=3.進(jìn)一步,由方程3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)可得ks=2,n=72,故方程Z(SL(n))=φ3(n)在這種情形下的解只有n=72.

綜上所述,定理1.3結(jié)論成立.

定理1.4的證明令n=2kp1k1p2k2…psks,其中p1,p2,…,ps都是素?cái)?shù),s,k1,k2,…,ks∈N,在以下三種情況下討論方程Z(SL(n))=φe(n)(e=4)的解:

(i) 顯然,Z(SL(1))≠φ4(1),Z(SL(2))≠φ4(2),Z(SL(3))≠φ4(3),Z(SL(4))≠φ4(4),即n=1,2,3,4不是方程Z(SL(n))=φ4(n)的解.

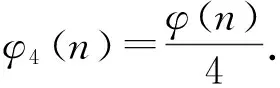
代入方程Z(SL(n))=φ4(n)可得4(2k+1-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1).

分兩種情形進(jìn)行討論:

(a) 若k=2,則n=4,4×2,經(jīng)檢驗(yàn),它們不是方程Z(SL(n))=φ4(n)的解.

(b) 若k=3,則n=8,8×3,8×5,8×7,8×3×5,8×7×5,8×3×7,8×3×5×7,經(jīng)檢驗(yàn),它們不是方程Z(SL(n))=φ4(n)的解.

(iii) 若psks=max{2k,p1k1,p2k2,…,psks},則k≥1.在這種情況下,由引理2.2可得SL(n)=psks,又由引理2.3可得Z(SL(n))=psks-1.

分兩種情形進(jìn)行討論:

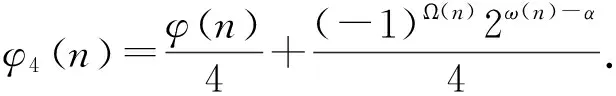
4(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2ω(n)-α.

在以下兩種情況下討論α:

當(dāng)α=k=0時(shí),根據(jù)ω(n)=s+1,由上式進(jìn)一步可得8(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2s+2.對(duì)方程兩邊同時(shí)取模ps-1可得0≡(-1)Ω(n)2s+2≡2s+2(modps-1),因此ps=2t+1(t∈N,1≤t≤s+2)是方程有解的必要條件.根據(jù)初等數(shù)論知識(shí),若ps=2t+1是一個(gè)素?cái)?shù),且t是2的平方,則ps是一個(gè)費(fèi)馬素?cái)?shù).到目前為止,只發(fā)現(xiàn)了5個(gè)費(fèi)馬素?cái)?shù).如果費(fèi)馬素?cái)?shù)只存在有限個(gè)的假設(shè)成立,那么方程Z(SL(n))=φ4(n)在這種情形下只存在有限個(gè)解.

當(dāng)α=k=1時(shí),根據(jù)ω(n)=s+1,由上式進(jìn)一步可得8(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)+(-1)Ω(n)2s+1.對(duì)方程兩邊同時(shí)取模ps-1可得0≡(-1)Ω(n)2s+1≡2s+1(modps-1),因此ps=2t+1(t∈N,1≤t≤s+1)是方程有解的必要條件.根據(jù)初等數(shù)論知識(shí),若ps=2t+1是一個(gè)素?cái)?shù),且t是2的平方,則ps是一個(gè)費(fèi)馬素?cái)?shù).到目前為止,只發(fā)現(xiàn)了5個(gè)費(fèi)馬素?cái)?shù).如果費(fèi)馬素?cái)?shù)只存在有限個(gè)的假設(shè)成立,那么方程Z(SL(n))=φ4(n)在這種情形下只存在有限個(gè)解.

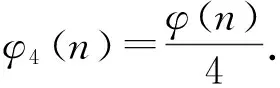
在以下兩種情形下討論ks:

當(dāng)ks=1時(shí),由上式進(jìn)一步可得4=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…ps-1ks-1-1(ps-1-1).進(jìn)一步,我們可以推導(dǎo)出k=3,n=8ps,則方程Z(SL(n))=φ4(n)在這種情形下的解為n=8ps.

當(dāng)ks>1時(shí),對(duì)方程3(psks-1)=2k-1p1k1-1(p1-1)p2k2-1(p2-1)…psks-1(ps-1)兩邊取模ps可得-4≡0(modps).顯然,這樣一個(gè)質(zhì)數(shù)ps不存在,故方程Z(SL(n))=φ4(n)在這種情形下無解.